Hindmarsh-Rose神经元阵列自发产生螺旋波的研究∗

2018-03-26汪芃李倩昀唐国宁

物理学报 2018年3期

汪芃李倩昀唐国宁

(广西师范大学物理科学与技术学院,桂林 541004)

1 引言

自从Winfree于1972年首次在化学系统中观察到螺旋波以来[1],人们在各种系统中,无论在可激发介质还是在一般介质上,都观察到了螺旋波[2−12].众所周知,心脏出现螺旋波电信号会导致危险的心律失常,如心动过速和心室纤维性颤动[7],从而危及生命.心脏中的螺旋波一般不会自发消失,除非螺旋波漫游出边界消失[7],否则会持续存在,需要人为干预才能消除,所以螺旋波的控制受到人们极大的关注[13,14].研究发现[8,15]:无论在药物引起的振荡中,还是睡眠状态下,在哺乳动物大脑皮层中都会自发出现螺旋波,只是螺旋波的寿命很短;癫痫发作时,在大脑皮层中也会循环出现螺旋波.螺旋波的存在可以在介观尺度上组织和调节皮层的群体活动,但是它们在哺乳动物大脑皮层中产生的机制和潜在功能仍然不清楚,需要进一步研究.

为了了解螺旋波在神经元系统中产生的机制,人们从理论和实验上进行了对噪声诱发螺旋波的研究.因为在宏观世界中被人们称为“噪声”的随机涨落是普遍存在的,虽然噪声给人们的第一印象是有害的,但是噪声和非线性系统在一定条件下会发生随机共振现象,促进非线性系统响应的增强.1998年,Jung等[16]首次在培养的神经胶质细胞网络中观察到由网络噪声诱发的螺旋化学波,这种螺旋波在噪声作用下也会自发消失;1999年,García-Ojalvo等[17]在可激发介质中也观察到噪声诱发的螺旋波.这些发现引起人们对噪声诱发螺旋波的极大兴趣[18−23].因为实际神经系统出现噪声是不可避免的,例如在大脑中,一个神经元通常与许多神经元有耦合,各神经元并不是处于同步状态,而是处于非同步状态,因此这种众多的非近邻耦合的总效果相当于在只考虑近邻耦合的神经元上施加一种噪声扰动.噪声可以诱发螺旋波,也可以使同质介质系统(由相同神经元组成的系统)处于混沌态,那么系统从随机的初相位分布态演化是否能自发形成螺旋波?迄今为止这个问题仍缺乏研究,对这一问题进行研究会有助于人们了解大脑中螺旋波产生的机制.

本文采用Hindmarsh-Rose(HR)神经元模型[24]研究了由同质神经元组成的二维阵列系统从具有随机相位分布的初态演化.我们发现,当单个HR神经元处于一周期态时,只要系统的耦合强度在一定范围内,系统都可以自发出现螺旋波,适当选取耦合强度和初态,系统还能自发出现圆形波等其他无螺旋波的态,以及出现同步振荡和振荡死亡现象.当单个HR神经元处于二周期态时,系统自发出现螺旋波的能力大为减少,这些结果对了解大脑中螺旋波的形成、癫痫和振荡死亡产生机制具有积极意义.

2 模型

本文采用1984年Hindmarsh和Rose提出的三变量的HR神经元模型来构造一个二维神经元阵列系统,该系统的动力学方程如下[24]:

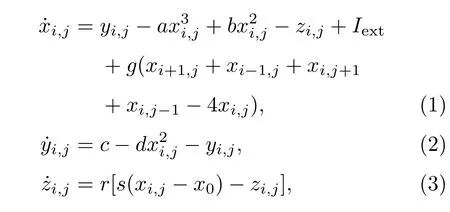
式中x代表神经元的细胞膜电位;y代表与内电流相关的恢复变量;z代表与钙离子激活的钾离子电流相关的慢变调节电流;a,b,c,d,r,s和x0为HR神经元模型参数;Iext为外部刺激电流;g为耦合强度;角标i,j=1,2,···,N代表N ×N个耦合的HR神经元.为了控制神经元系统的动力学行为,参考文献[20]中相关模型参数的取值,本文固定取a=1.0,b=3.0,c=1.0,d=5.0,r=0.006,s=4.0,x0= −1.6,N=200,Iext和g为可调参数,通过适当选择Iext的值,可使得单个神经元(在情况下方程(1)—(3)描述的系统)处于一周期、二周期等周期态,或者使单个神经元处于混沌态,本文只考虑单个神经元处于一周期和二周期的情况,数值解方程组采用欧拉法,时间步长取Δt=0.02,使用无流边界条件,每次数值模拟时间长度为12000单位时间.

系统变化状态为混沌时,对应的方差值变化也就较大.而当系统出现有序状态时,部分神经元振荡趋于一致,此时方差值也趋于稳定.因此,方差可以较好地描述系统的状态变化.为了描述二维神经元阵列系统状态变化情况,引入系统方差:

当σ无规变化时,系统处于混沌态;如果σ有规律变化,系统处于有序态;如果σ趋于0,系统处于同步态.

3 数值模拟结果

系统的演化结果与系统初态和耦合强度有关,由于系统初态很多,为了比较不同初态演化效果,规定系统初态中各神经元膜电位x＞0数量与神经元总数之比为ρ.本文通过以下方式产生系统演化的初态:在耦合强度g=0和给定Iext的情况下,给系统的每一个神经元赋随机初值,让系统演化2000个时间单位后,找ρ满足给定值的系统状态作为g/=0和给定Iext情况下系统的初态,该初态具有混沌初相位分布,一般ρ值在2%—8%之间.在下面的数值模拟中,我们都会选择不同ρ值的不同初态进行数值模拟研究,在没有特别指出的情况下,给出的斑图都是系统演化12000单位时间后的斑图.考虑到耦合强度很小时,系统不会自发出现单个螺旋波,耦合强度取值大于0.1.

3.1 一周期态的结果

固定Iext=1.315,这时单个神经元处于一周期态,研究在相同ρ值下系统从不同初态演化是否自发出现螺旋波.考虑到取不同ρ值都得到类似结果,这些结果与三种类型的初态有关.下面取ρ=5%和三个典型的初态,分别记为初态1、初态2和初态3.为了衡量初态的差异,将单个神经元状态的周期变化分成5个阶段,如图1(a)所示,图中相邻两个黑点之间的状态变化为一个阶段,图中数字为阶段的编号.在初态1下,处于阶段1至阶段5的神经元数与总数之比γ分别为γ1=82.75%,γ2=11.03%,γ3=0.938%,γ4=5.28%,γ5=0%;同理得到初态2的各阶段占比分别为γ1=0.045%,γ2=4.425%,γ3=4.323%,γ4=91.207%,γ5=0%;初态3的各阶段占比分别为γ1=71.195%,γ2=14.058%,γ3=2.13%,γ4=10.788%,γ5=1.825%.这三个典型态初态的特点是:初态1的γ1=82.75%,处于阶段1的神经元占绝大多数;初态2的γ4=91.207%,处于阶段4的神经元占绝大多数;初态3下的γ5=1.825%,处于阶段5的神经元占比不为0,处于比较均匀的分布;图1(b)—(d)分别给出三个初态的x变量斑图,可以看出,系统初态中各神经元具有无规的初相位分布.

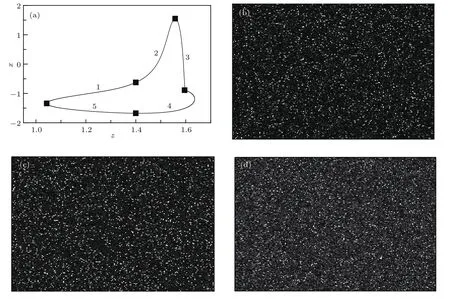
图1(a)单个HR神经元的吸引子在z-x平面上的投影和(b)初态1、(c)初态2、(d)初态3对应的x变量斑图Fig.1.(a)The attractor of the single HR neuron in(z,x)projection and the patterns of variable x for(b)the initial state 1,(c)the initial state 2,and(d)the initial state 3.

下面先使用初态1,研究系统的演化.图2给出了不同耦合强度下方差随时间的变化,图3给出了与图2对应参数下x变量的斑图,图2和图3结果对比如下.

1)在无耦合下单个神经元周期振荡,导致系统方差规则变化.

2)在0.1＜g＜2.9的情况下,系统经过暂态后一般自发出现多个螺旋波和螺旋波对,出现螺旋波与初态无关.耦合强度不同,螺旋波和螺旋波对的位置和大小不相同(即斑图不同),螺旋波的数量与耦合强度有关,这表明螺旋波的出现具有偶然性,因此不同初态和不同耦合强度时,斑图一般都不一样.一般有这样的规律:当耦合强度较小时,神经元簇状放电的峰个数少,螺旋波的波臂较细,因此螺旋波尺寸小,数量就多,系统不存在单个螺旋波;增大耦合强度,神经元簇状放电的峰个数增多,螺旋波波臂变粗,系统中螺旋波尺寸就大,数量相应就少,所以适当选择耦合强度可以得到单螺旋波.通常多个螺旋波和螺旋波对相互作用导致规则或无规则斑图在系统中重复出现,方差接近规则变化,如图2(b)—(e)所示.这些结果表明系统出现单螺旋波的概率比较小,尺寸小的螺旋波出现的概率比较大,这些结果与实验观察到的结果一致.实验观察到[16]:在背景网络噪声(由红藻氨酸浓度调节)作用下胶质细胞网络中自发出现螺旋波,小尺寸螺旋波出现的概率大,大尺寸螺旋波出现的概率小.

3)在g≥3.0的情况下,系统一般不会出现螺旋波,一般出现圆形波或环形波,它们相互作用导致系统出现平面波、不规则的曲线波等斑图.图3(e)所显示的亮斑就会形成圆形波,但是这种圆形波不稳定,会随时间变化,在该状态下,存在所有神经元满足x＜0,因此系统方差表现为无规律大幅度振荡变化.在数值模拟中,我们在g=2.84,4.3,4.5,4.8情况下分别观察到单个螺旋波,如图3(d)和图3(f)所示.

4)从图3可以看出,螺旋波的波臂存在明显的无规律明暗分布,这是因为在螺旋波态下,神经元簇状放电有多个峰,而不是一周期态的单个峰,而且峰的数量及高度和间隔都在无规则变化,这是导致在螺旋波态下系统方差随时间变化不是很有规律的原因.

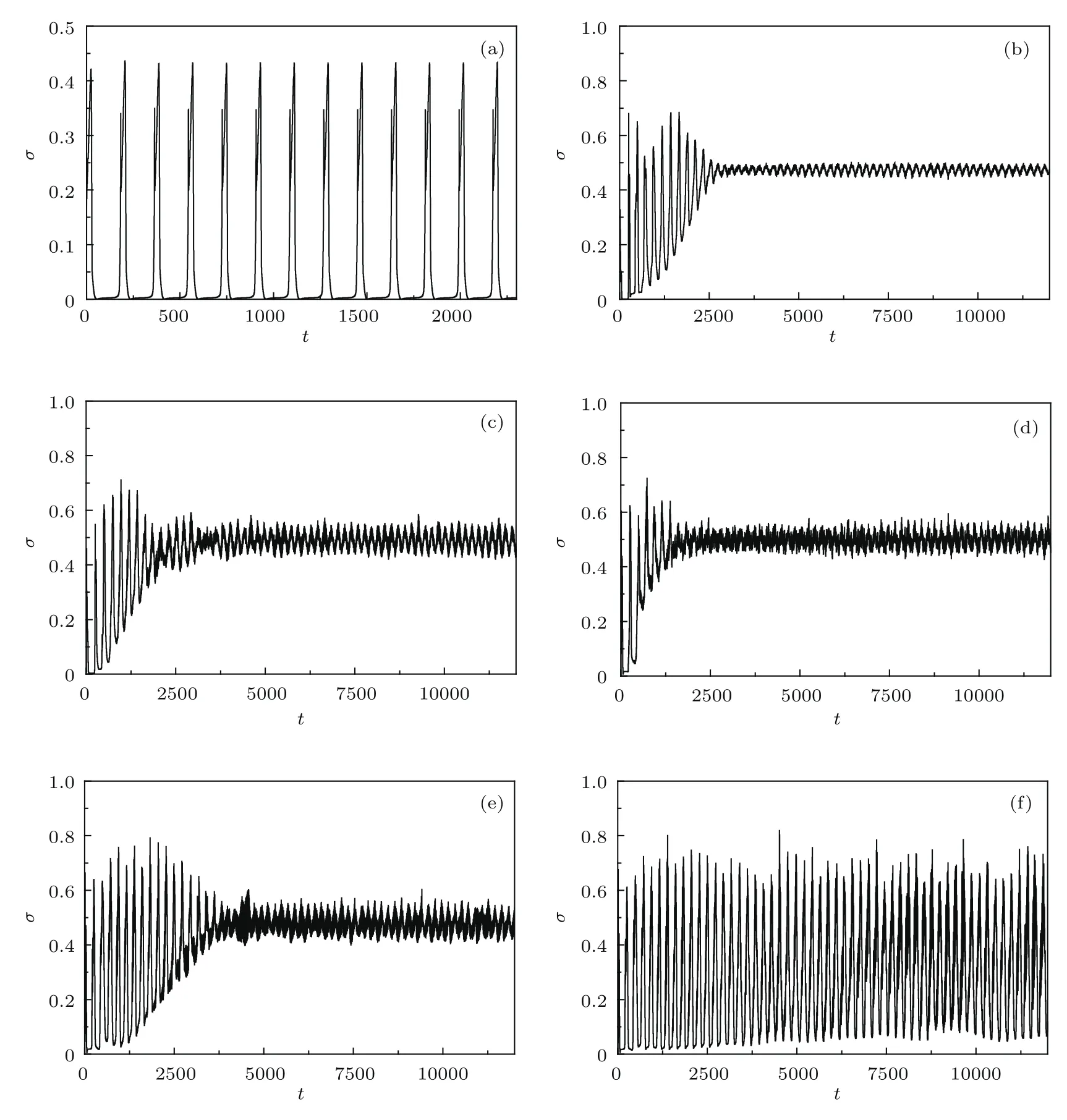
图2 在使用初态1和不同耦合强度下方差随时间的变化(a)g=0;(b)g=0.2;(c)g=1.2;(d)g=2.2;(e)g=2.84;(f)g=3.0Fig.2.The time evolution of the variance for different values of coupling strength when the initial state 1 is applied:(a)g=0;(b)g=0.2;(c)g=1.2;(d)g=2.2;(e)g=2.84;(f)g=3.0.

图3 在使用初态1和不同耦合强度下x变量的斑图(a)g=0.2;(b)g=1.2;(c)g=2.2;(d)g=2.84;(e)g=3.0;(f)g=4.3Fig.3.Pattern of the variable x for different values of coupling strength when the initial state 1 is applied:(a)g=0.2;(b)g=1.2;(c)g=2.2;(d)g=2.84;(e)g=3.0;(f)g=4.3.

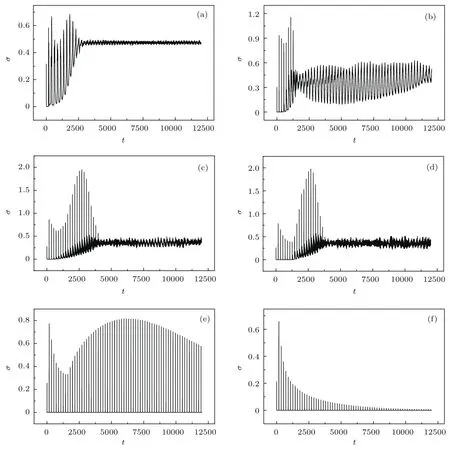
图4 在使用初态2和不同耦合强度下方差随时间的变化(a)g=0.2;(b)g=0.5;(c)g=1.0;(d)g=1.4;(e)g=1.5;(f)g=2.5Fig.4.The time evolution of the variance for different values of coupling strength when the initial state 2 is applied:(a)g=0.2;(b)g=0.5;(c)g=1.0;(d)g=1.4;(e)g=1.5;(f)g=2.5.

下面使用初态2,研究系统的演化.图4给出了在不同耦合强度下方差随时间的变化,图5给出了与图4对应参数下x变量的斑图.从图4和图5可以看出:当0.1＜g≤0.5时,系统很容易出现螺旋波和螺旋波对,只是随耦合强度增加,系统出现小螺旋波和螺旋波对所用时间不断增加;当0.5＜g≤1.4时,系统不容易出现螺旋波,只是在适当的耦合强度下才出现螺旋波,参见图5(c),这时系统较容易出现不规则的平面波,参见图5(c)和图5(d),方差无规律小幅变化;当g≥1.5时,方差大部分时间接近0,当神经元状态处于阶段2和3时,方差才比较大,如图5(e)和图5(f)所示,这表明系统整体出现间歇式全局同步振荡,而且随着耦合强度的增加,系统整体同步程度逐渐增强.神经元容易同步的原因是,绝大部分神经元处于阶段4,各神经元膜电位的值差别不大,通过膜电位耦合就容易实现全局同步.系统出现间歇同步的原因是,当神经元状态处于阶段4和5时,尽管方差接近0,但是神经元并没有达到精确全局同步,x变量的差的最大值在千分之二左右,而且系统的x变量的弱非均匀分布呈中心在对角的靶波状,这样当神经元状态处于阶段2时,神经元出现依次被激发,导致系统方差又增大,当神经元处于阶段4时,神经元又处于接近精确全局同步,方差又接近0.

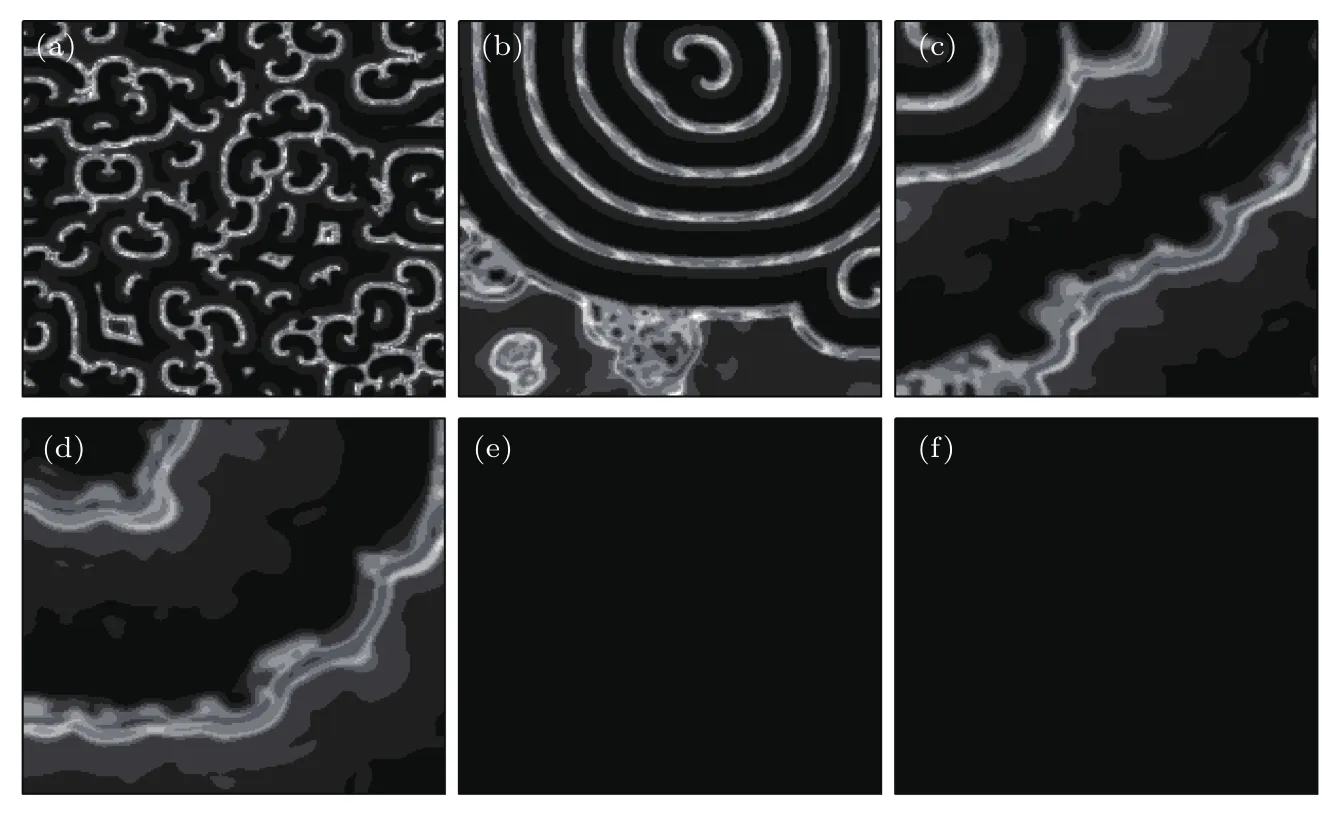
图5 在使用初态2和不同耦合强度下x变量的斑图(a)g=0.2;(b)g=0.5;(c)g=1.0;(d)g=1.4;(e)g=1.5;(f)g=2.5Fig.5.Pattern of the variable x for different values of coupling strength when the initial state 2 is applied:(a)g=0.2;(b)g=0.5;(c)g=1.0:(d)g=1.4;(e)g=1.5;(f)g=2.5.

最后使用初态3研究系统的演化,同样得到:当耦合强度在[0.2,0.9]范围时,系统都很容易产生螺旋波,且随着耦合强度的增加,螺旋波或螺旋波对的数量逐渐减少,与前两种初态演化结果一致,当g=0.9时,系统出现单个螺旋波;当g≥1.0时,系统快速进入振荡死亡,所有神经元振荡方式演化到不动点x=−1.31742,y=−7.687,z=1.13032,如图6所示.产生振荡死亡的原因是,不动点靠近阶段5和阶段1,当初态中的神经元处于阶段5的比率足够大时,就可以出现振荡死亡.为了证明是处于阶段5的神经引起振荡死亡,通过取不同ρ值(在2%—8%范围内)的初态,发现只要,不论初态是γ1最大或还是γ4最大都会出现振荡死亡现象,而且γ5越大,达到振荡死亡需要的耦合强度就越小.

图6 在使用初态3和g=1.0情况下系统中某个神经元在z-x平面上的相图Fig.6.Phase diagram of a neuron in the system on the plan(z,x).The initial state 3 and g=1.0 are applied.

以上是取ρ=5%时得到的结果,当ρ取其他值时,同样得到:当耦合强度在小于临界值gc的一个范围内取值时,系统容易出现螺旋波和螺旋波对,增大耦合强度,螺旋波和螺旋波对的数量将减少,偶尔出现单个螺旋波;当耦合强度大于临界值gc时,系统出现三种不同的动力学行为,分别对应三类初态.系统从第一类初态演化,一般不容易出现螺旋波,而是出现圆形波,只有适当选择耦合强度才能出现螺旋波;不同耦合强度会得到不同斑图,即使出现单螺旋波斑图,其波头位置也可能不同;系统从第二、三初态演化,在大的耦合强度下同样分别观察到了同步振荡和振荡死亡现象.

3.2 二周期结果

当固定Iext=1.60,这时单个神经元处于二周期态.选择不同ρ值,研究系统从不同初态演化,观察到两种演化结果,分别对应两类初态,一类初态不能使系统自发出现螺旋波,另一类初态能使系统出现螺旋波,但是只能在一定的耦合强度范围内才能出现螺旋波,出现螺旋波的耦合强度范围比一周期情况大为缩小.图7给出了与图1类似的结果,这里仍取ρ=5%.将神经元二周期振荡分成4个阶段,如图7(a)所示,图7(b)和图7(c)是两个典型的初态,分别记为初态4和初态5.初态4的γ1=50.515%,γ2=18.895%,γ3=6.89%,γ4=23.7%,其分布特点是不够均匀,因为γ3偏小;初态5的γ1=34.19%,γ2=26.13%,γ3=10.07%,γ4=29.645%,其分布特点是比较均匀.

图8给出了系统从初态4和5演化得到的部分结果.系统从初态4演化的研究结果是:当0.2≤g≤0.4时,系统只能产生小波,最终形成向中心传播方形波,即反靶波,如图8(a)和图8(b)所示;当g≥0.5时,系统形成圆形波,如图8(c)所示.产生圆形波的原因是,处于阶段3的神经元较少,相当于振荡的循环过程,少了一个过程,而螺旋波、靶波形成必须有四个过程,所以系统演化过程不容易形成螺旋波和靶波.

图7(a)单个HR神经元的吸引子在z-x平面上的投影和(b)初态4、(c)初态5对应的x变量斑图Fig.7.(a)The attractor of the single HR neuron in(z,x)projection and the patterns of variable x for(b)the initial state 4 and(c)the initial state 5.

图8 不同初态和不同耦合强度下x变量的斑图(a)初态4,g=0.3;(b)初态4,g=0.4;(c)初态4,g=0.8;(d)初态5,g=0.2;(e)初态5,g=1.4;(f)初态5,g=1.6Fig.8.The patterns of variable x for different coupling strengths and initial states:(a)The initial state 4 and g=0.3;(b)the initial state 4 and g=0.4;(c)the initial state 4 and g=0.8;(d)the initial state 5 and g=0.2;(e)the initial state 5 and g=1.4;(f)the initial state 5 and g=1.6.

系统从初态5演化的研究结果是:当g=0.2时,系统开始只能产生小波,最终形成了螺旋波;当g=0.3时,系统产生的波与图8(a)相似;当0.4≤g≤1.3时,系统出现多个螺旋波和螺旋波对;当g=1.4,1.5时系统出现单个螺旋波,如图8(e)所示;当g≥1.6时,系统只出现圆形波,如图8(f)所示.可见只有当神经元的初相位分布比较均匀时系统才能产生螺旋波,耦合强度过大和过小都不能产生螺旋波.

从上面的结果可以看出,单个神经元处于一周期态时,系统比较容易出现螺旋波,而且出现螺旋波的耦合强度范围较宽.单个神经元处于二周期态时,系统只有在神经元的初相位分布比较均匀时才能产生螺旋波,因此神经元处于更高周期态,系统较难自发出现螺旋波,数值模拟也得到这样的结论.

4 结论

采用HR神经元模型,研究神经元阵列系统从一个具有随机初相位分布的初态演化是否能自发形成螺旋波(包括螺旋波对),随机的初相位分布模拟了神经元的非近邻耦合行为,发现系统是否能自发形成螺旋波与系统初态、单个神经元的状态、耦合强度有关,且单个神经元的状态对系统形成螺旋波影响最大.

当单个神经元处于一周期态时,系统从任意初态演化,在一定的耦合强度范围内,系统都能自发产生螺旋波和螺旋波对,还观察到其他有序斑图(如平面波、反靶波、圆形波);初态相同而耦合强度不同或者是耦合强度相同而初态不同时,系统演化一般会得到不同结果;当耦合强度超过临界值后,系统不容易自发形成螺旋波,演化结果依赖初态.我们观察到两种重要现象:1)当系统初态中处于阶段4的神经元占绝大多数时,系统会演化到间歇全局周期振荡态上,甚至实现精确全局同步振荡;2)当系统初态中处于阶段5的神经元数量足够多时,系统就会出现振荡死亡现象.如果系统不出现间歇全局同步振荡和振荡死亡,在大的耦合强度下系统一般出现圆形波.

当单个神经元处于二周期态时,只有当各神经元的初相位分布比较均匀时才可以自发出现螺旋波,而且出现螺旋波的耦合强度范围相比一周期情况有较大的缩小;当单个神经元处于更高周期态时,系统越不容易自发出现螺旋波.

上述结果有助于了解大脑皮层中螺旋波是如何自发形成的,特别是能帮助人们了解癫痫产生的机制,因为癫痫是大量神经元同步引起的一种功能性脑失调[25].本文结果能够回答同步振荡是如何产生的,而且大量神经元的振荡死亡形成机制也为治疗癫痫提供了有用信息.

[1]Winfree A T 1972 Science 175 634

[2]Larionova Y,Egorov O,Cabrera-Granado E,Esteban-Martin A 2005 Phys.Rev.A 72 033825

[3]Plapp B P,Egolf D A,Bodenschatz E,Pesch W 1998 Phys.Rev.Lett.81 5334

[4]Müller S C,Plesser T,Hess B 1985 Science 230 661

[5]Vanag V K,Epstein I R 2001 Science 294 835

[6]Foerster P,Müller S C,Hess B 1990 Development 109 11

[7]Davidenko J M,Pertsov A V,Salomonsz,Baxter W,Jalife J 1992 Nature 355 349

[8]Huang X,Xu W,Liang J,Takagaki K,Gao X,Wu J 2010 Neuron 68 978

[9]Huang X,Troy W C,Yang Q,Ma H,Laing C R,SchiffS T,Wu J Y 2004 J.Neurosci.24 9897

[10]Chen J X,Zhang H,Qiao L Y,Liang H,Sun W G 2018 Commun.Nonlinear Sci.Numer.Simulat.54 202