双色高频激光作用下原子低阶次谐波的理论研究∗

宋文娟1)2) 郭福明1)2) 陈基根3) 杨玉军1)2)†

1)(吉林大学原子与分子物理研究所,长春 130012)

2)(吉林省应用原子与分子光谱重点实验室,长春 130012)

3)(台州学院物理与电子工程学院物理与材料工程系,台州 318000)

1 引 言

随着激光技术的发展,利用原子内壳层电子跃迁、强激光与物质相互作用产生的高次谐波辐射及自由电子激光,均可获得极紫外和X射线波段的光源[1−12].这些光源的制备方案已逐渐成熟并应用于更广的领域,如高次谐波发射不但可以用来产生高频率光,而且由于其频谱存在一个强度相近的平台结构,被应用于阿秒尺度超短光脉冲的产生及远紫外波段光学频率梳的制备[13−15].自由电子激光的特点是频率在一定范围内可调,时间尺度从几个飞秒到几十个飞秒,强度可达到1019W/cm2.由于其超短时间分辨性和极小空间分辨特性,被用来探测超快电子运动及对纳米尺度的材料成像[16−18].

与传统的红外驱动激光相比,这些高强度、高频率激光与原子发生作用,仍然可以观察到很多非线性现象,如高次谐波发射、阈上电离和原子电离稳定等[19−28].而且在高频条件下,原子光发射会呈现出一些新特征.如谐波谱没有清晰明确的截止能量,三步模型给出的截止规则不再适用[20];在长脉冲高频强激光作用下,除了观察到奇次谐波发射外,还能看到清晰的超拉曼辐射,这与原子势函数本征态之间的跃迁相关[21];对于高频短脉冲与原子相互作用,随着入射光强的增加,谐波峰值位置逐渐劈裂为多峰结构,激光脉冲上升沿和下降沿对光发射的作用越来越大[22].

随着实验技术的进一步发展,目前人们关注的重点逐渐从单色场过渡到双色抽运探测研究,该方案可以对体系中电子超快运动过程进行测量.双色高频激光脉冲的研究方案已在实验上实现并得到应用[29−33],如用于研制双光子光谱仪及抽运探测仪等[34−38].基于频域理论,Liu等[39]研究了连续双色高频激光作用下原子阈上电离电子的角分布.在实验上,Antaris等[40]利用强度较低的双色自由电子激光对蛋白质结构进行了成像研究,对于较高光强作用下的相关实验研究尚未见到报道.关于高强度双色高频光作用下原子分子光发射现象的机理和规律,人们的认识还不够全面、清晰.本文采用数值求解含时薛定谔方程(TDSE)方案,系统地研究了原子在双色高频激光脉冲辐照下的光发射过程.研究结果表明,在双色高频激光脉冲作用下,除了观察到谐波发射外,还发现了新的频率光发射.并对这种辐射光随入射高频光的频率、强度的变化规律进行了研究.如无特殊说明,本文均采用原子单位.

2 理论方法

为研究双色高频激光作用下原子的光发射过程,需要数值求解原子在强激光作用下的TDSE.在长度规范和偶极近似下,该方程表示为

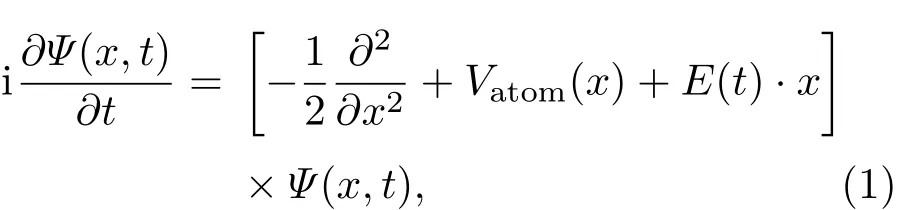
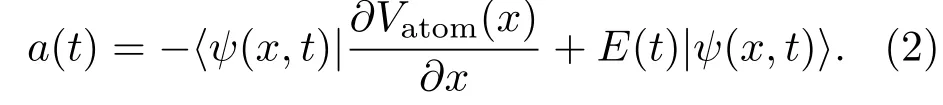
根据含时偶极矩,可计算原子的光发射谱:

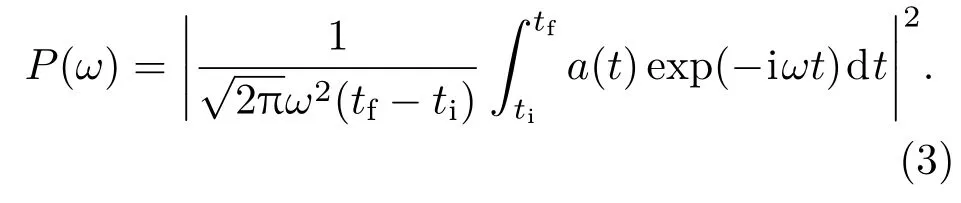
为检验结果的准确性,将结果与三维动量空间计算进行了比较.在三维动量空间计算方案下,体系含时波函数Φ(k,t)满足的TDSE表示为

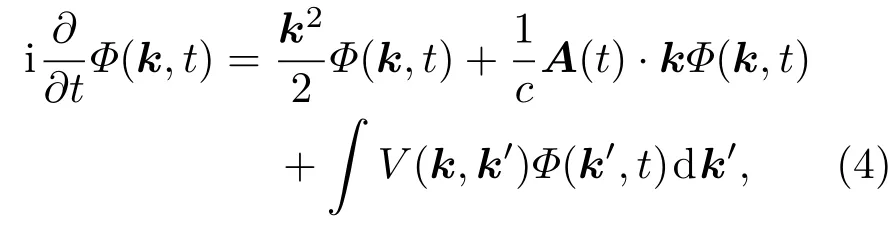
其中V(k,k′)为动量空间下的原子势.本文采用含时伪谱方案对方程(4)进行求解[43−46].

3 结果与讨论

本文先研究了脉宽为100个光学周期、强度为1015W/cm2、频率分别为ω1=1和ω2=1.2的高频激光脉冲辐照原子产生的谐波谱,如图1中的黑色实线和红色点线所示.由图1可知:单色高频激光的谐波谱中除了可观测到基频光外,还可获得三次和五次谐波辐射;此外,在能量为0.375位置可以观察到较强的光发射,这个发射峰值对应体系第一激发态和基态之间的跃迁.当上述频率为ω1=1和ω2=1.2的两束高频激光脉冲同时辐照原子时,在其谐波谱(图1中的绿色点划线)中,既有频率为1和1.2的高频激光的一、三及五次谐波发射,同时又产生了很多新的伴峰,且每个阶次谐波附近相邻峰之间的能量间距为0.2.

图1 入射激光脉冲强度为1015W/cm2时,频率分别为ω1=1(黑色实线),ω2=1.2(红色点线)的脉冲及两者组合的脉冲(绿色点划线)辐照原子产生的光发射Fig.1.High-order harmonic spectra from atom in the one-color laser pulses with high frequencies 1(black solid curve)and 1.2(red dotted curve),respectively.The green dash-dotted curve shows the harmonic spectrum from the combined two-color laser pulse.The intensities of these laser pulses are 1015W/cm2.

为分析双色高频场下谐波光发射行为的普遍规律,首先固定其中一束入射光脉冲频率ω1=1,改变另一束入射激光频率ω2,观察其发射谱的变化.从图2可以看出,随着ω2的增加,每一阶次谐波光发射谱逐渐从单峰过渡到多峰结构,相邻峰之间的间距逐渐增加,并且间距始终等于两个入射激光的频率差.此外,从图2还可观测到由第一激发态到基态之间跃迁产生的光发射位置并未随着入射激光频率的改变而发生变化,始终为0.375.

图2 不同双色高频激光脉冲的谐波谱,其中第一束激光频率为ω1=1,第二束激光脉冲的频率从1增到1.3,其他双色激光脉冲的参数和图1参数相同Fig.2.Harmonic spectra from two-color highfrequency laser pulses.Here,one frequency of the two-color pulse is set as 1,and the other frequency increases from 1 to 1.3.The other parameters of the two-color pulse are the same as those of Fig.1.

同时,本文研究了双色高频激光辐射谱中峰值处的谐波效率随ω2的强度变化,如图3所示,ω2的强度从Iω2=1014W/cm2增强到Iω2=1016W/cm2.图3给出了一次谐波附近的六个辐射峰值的强度变化.随着入射光ω2强度的增加,光辐射峰值的强度变化规律存在较大差别.对于频率为ω=ω1的光辐射,开始阶段,其发射强度几乎不随入射光ω2光强的改变而改变;当入射光ω2的强度大于1015W/cm2后,光强度逐渐减小.产生这一现象的原因是,在更高光强的入射光ω2作用下,体系基态逐渐耗尽.对于其他频率的光辐射峰,在开始阶段,它们的强度均随着ω2入射光强的增加而增加.对于频率ω=1.2和ω=0.8的光辐射,其强度增加的幅值正比于入射光ω2的光强.而更高频率ω=1.4和更低频ω=0.6的光辐射强度,随着入射光ω2强度的平方呈线性增加.当入射高频光ω2的光强超过1015W/cm2之后,由于基态耗尽效应,上述光辐射峰的强度增速放缓甚至减弱.

图4给出了三次谐波附近的原子光辐射随着入射光ω2强度的变化.从图4可以看出,对于ω1的三次谐波发射强度,随着入射光强的改变很小,当体系基态电离较大时,其辐射强度逐渐降低.对于ω2的三次谐波发射ω=3.6,其强度变化正比于其入射光强的三次方.当入射光ω2光强很小时,只能观察到ω1的三次谐波和较弱的ω=3.2的光辐射:随着ω2光强的逐渐增加,其三次谐波强度也逐渐增加,而ω=3.2的发射强度正比于的发射强度正比于从图4可注意到,当入射激光ω2的光强较弱时,辐射峰ω=3的强度最强;当Iω2=0.5×1015W/cm2时,其伴峰ω=3.2辐射强度与其接近;当光强进一步增强时,其伴峰ω=3.2辐射强度超过ω=3强度;当强度超过1015W/cm2时,另一个伴峰ω=3.4的强度逐渐超过了ω=3.2的发射强度;若Iω2的强度进一步增强,ω2的三次谐波辐射强度达到最高,超过所有伴峰的辐射强度.对于更高能量的光辐射,如ω=3.8,随着ω2的强度增加,其辐射强度增加的更为迅速,但由于其截面很小,使得它在原子谐波谱中的强度相对较弱.

图3 双色高频激光谐波谱中一次谐波附近的六个辐射峰值转化效率随ω2强度的变化,其他激光参数和图1参数相同Fig.3.The intensities of the six emission peaks near the first-order harmonic as a function of the intensity of the laser pulse with frequency 2.The other parameters of the two-color laser pulse are the same as those of Fig.1.

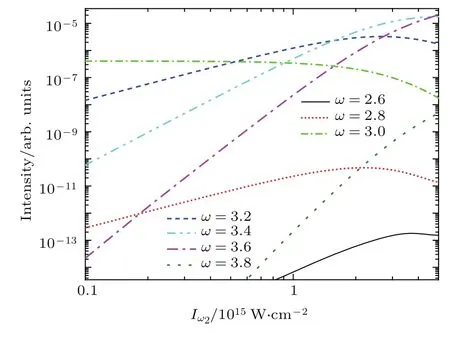
图4 双色高频激光谐波谱中三次谐波附近的七个辐射峰值转化效率随ω2强度的变化,其他激光参数和图1参数相同Fig.4.The intensities of the seven emission peaks near the three-order harmonic as a function of the intensity of the laser pulse with frequency 2.The other parameters of the two-color laser pulse are the same as those of Fig.1.

对于光辐射的瞬态行为可通过对其含时偶极矩进行小波变换得到[43].图5给出了驱动激光脉冲强度为1015W/cm2、频率分别为ω1=1和ω2=1.2时三次谐波附近的原子光发射行为.从图5可以看到,在激光脉冲持续时间内原子均有光辐射产生,其发射强度正比于入射激光强度,在入射光包络峰值附近发射最强.在伴峰中间也可以看到较强的辐射,这部分辐射强度随着时间振荡.通过对组合电场的分析发现这部分强度振荡产生的原因是叠加电场的即时振荡.

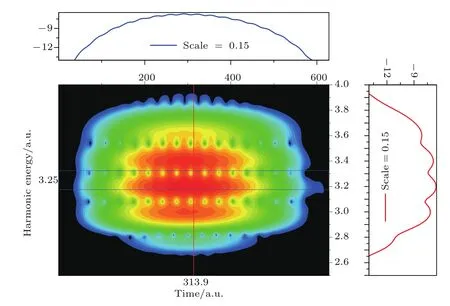
图5 驱动激光强度为1015W/cm2,频率分别为ω1=1,ω2=1.2组合脉冲作用下,原子光辐射的时间频率行为Fig.5.Time-frequency diagram of harmonic spectrum in the two-color field synthesized by a pulse with frequency 1 and the other one with frequency 1.2,respectively,and the intensities of the two pulses are 1015W/cm2.

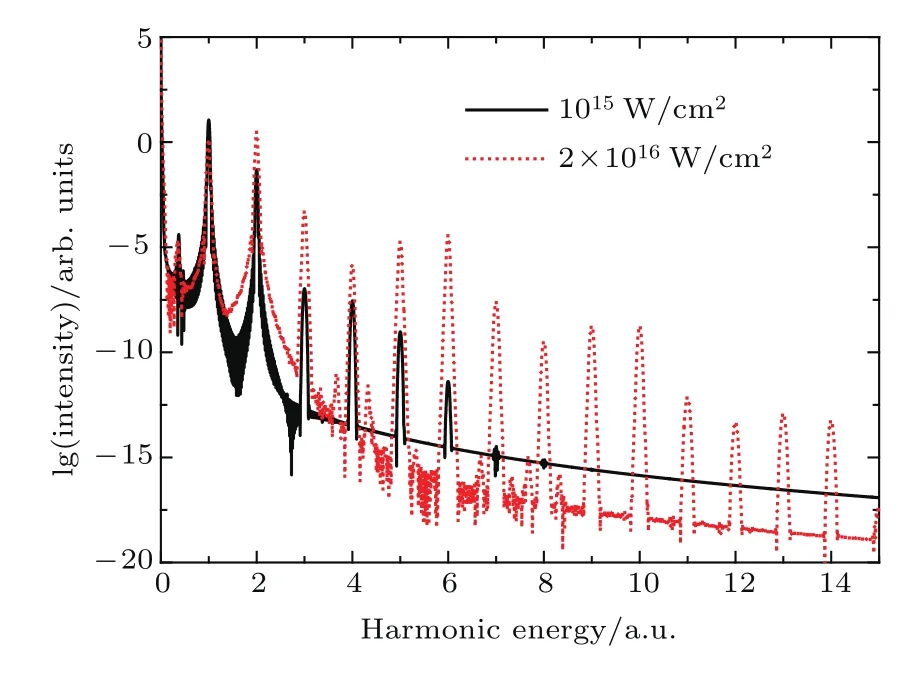
图6 等幅双色激光(频率分别为ω1=1与ω2=2)组合脉冲作用下的原子发射光谱,入射激光强度分别为1015W/cm2(黑色实线)和2×1016W/cm2(红色点线)Fig.6.High-harmonic spectra of the two-color laser pulse with one frequency 1 and the other 2.The laser peak intensities are 1015W/cm2(black solid curve)and 2×1016W/cm2(red dotted curve).

进一步研究了等幅双色组合激光脉冲的原子光发射谱,如图6所示.这里选定组合场中一束入射激光频率为ω1=1,另一束入射激光频率ω2=2,激光脉冲持续时间为50个光学周期,激光强度由1015W/cm2增大到2×1016W/cm2.从图6可以清晰地看到,在能量为整数的位置均有光辐射产生,整体的光发射谱在入射激光光强较大时大体呈现出多个平台结构(红色点线),每个平台的宽度为4.而入射光强较小时(黑色实线),由于谐波频谱截止能量较小,多平台特征体现不出.同时计算了持续时间为100个光学周期的情况,结果与50周期基本相同.说明在较长的脉冲持续时间下,上述规律与入射激光持续时间依赖性不强.变化另一束脉冲的频率,可以观察到类似的结果.由此可以看出,利用双色方案,可以根据需求,产生所需频率的高频光源.由于光谱平台结构的存在,可以应用该方案产生超短脉冲串,应用于电子超快动力学过程的研究.此外,对自由电子激光的激光参数准确测量通常存在困难.如果在准确标定一束激光参数的基础上,通过改变另一束激光参数,观察其组合脉冲与原子相互作用产生的光辐射信息,能够实现对其激光参数的准确标定.

为了确认结果的可靠性,将该结果与三维动量空间的计算进行了比较,如图7所示.组合激光脉冲的持续时间为100个光学周期,激光频率分别为ω1=1和ω2=1.2,激光的强度均为1015W/cm2.从图7可看出,一维和三维的计算结果定性上符合得非常好,原子发射谱均呈现出多峰值结构,峰值的位置以及峰值的强度分布均一致.二者的差别在于光辐射的发射效率不同,这可以归因于一维计算和三维计算的电离概率以及复合截面的差别.这一结果表明,本文在一维条件下预言的双色高频激光脉冲驱动原子产生等频率间隔多峰结构的光发射特性,不依赖于空间维度和理论算法,物理规律上具有普遍性.

图7 双色激光强度分别为Iω1=1015W/cm2,Iω2=1015W/cm2,激光频率分别为ω1=1和ω2=1.2的组合脉冲辐照一维模型原子(黑色实线)和真实原子(红色点线)产生的原子发射谱Fig.7.Harmonic spectra of the one-dimensional model atom(black solid curve)and real atom(red dotted curve)in a two-color laser pulse with one frequency 1 and the other 1.2.The intensities of the two pulses are equally intense and their peak intensities are chosen as 1015W/cm2.

4 结 论

本文通过数值求解TDSE系统地研究了高频双色激光脉冲与原子相互作用的光辐射.结果表明,光辐射中除了两束激光脉冲的基频辐射外,还可观察到其高阶谐波辐射及与这些辐射能量相差为两束入射激光频率差的辐射.通过改变其中一束入射激光的频率和强度,分析了光辐射的变化规律.利用该规律,可以利用优化双色方案产生所需频率的高频相干光源和超短光脉冲.

感谢吉林大学超算中心的计算支持.

[1]Ozaki T,Ganeev R A,Ishizawa A,Kanai T,Kuroda H 2002 Phys.Rev.Lett.89 253902

[2]Pert G J 2007 Phys.Rev.A 75 023808

[3]Mcpherson A,Gibson G,Jara H,Johann U,Luk T S,Mcintyre I A,Boyer K,Rhodhes C K 1987 J.Opt.Soc.Am.B 4 595

[4]Ferray M A,L’Huillier A,Lompre L A,Mainfray G,Manus C 1988 J.Phys.B:At.Mol.Opt.Phys.21 L31

[5]Dromey B,Zepf M,Gopal A,Wei M S,Tatarakis M 2006 Nat.Phys.2 456

[6]Emma P,Akre R,Arthur J,Bionta R,Bostedt C,Bozek J,Brachmann A,Bucksbaum P,Coffee R,Decker F G,Ding Y,Dowell D,Edstrom S 2010 Nat.Photon.4 641

[7]Huang Z,Brachmann A,Decker F J,Ding Y,Dowell D,Emma P,Frisch J,Gilevich S,Hays G,Hering P,Iverson R,Loos H,Miahnahri A,Nuhn H D,Ratner D,Stupakov G,Turner J,Welch J 2010 Phys.Rev.Spec.Top.Acc.Beams 13 020703

[8]Ishikawa T,Aoyagi H,Asaka T,Asano Y,Azumi N,Bizen T 2012 Nat.Photon.6 540

[9]Ackermann W,Asova G,Ayvazyan V,Azima A,Baboi N,Bahr J,Balandin V,Beutner B,Brandt A 2007 Nat.Photon.1 336

[10]Shintake T,Tanaka H,Hara T,Tanaka T,Togawa K,Yabashi M 2008 Nat.Photon.2 555

[11]Allaria E,Appio R,Badano L,Barletta W A,Bassanese S,Biedron S G,Borga A,Busetto E 2012 Nat.Photon.6 699

[12]Scott D J,Clarke J A,Baynham D E,Bayliss V,Bradshaw T,Burton G,Brummitt A,Carr S,Lintern A,Rochford J,Taylor O,Ivanyushenkov Y 2011 Phys.Rev.Lett.107 174803

[13]Goulielmakis E,Schultze M,Hofstetter M,Yakovlev V S,Gagnon J,Uiberacker M,Aquila A L 2008 Science 320 1614

[14]Krausz F,Ivanov M 2009 Rev.Mod.Phys.81 163

[15]Cingoz A,Yost D C,Allison T K,Ruehl A,Fermann M E,Hartl I,Ye J 2012 Nature 482 68

[16]Fang L,Osipov T,Murphy B F,Rudenko A,Rolles D,Petrovic V S,Bostedt C,Bozek J D,Bucksbaum P H,Berrah N 2014 J.Phys.B:At.Mol.Opt.Phys.47 124006

[17]Minitti M P,Budarz J M,Kirrander A,Robinson J S,Ratner D,Lane T J,Zhu D,Glownia J M,Kozina M,Lemke H T,Sikorski M,Feng Y,Nelson S,Saita K,Stankus B,Northey T,Hastings J B,Weber P M 2015 Phys.Rev.Lett.114 255501

[18]Treusch R,Feldhaus J 2010 New J.Phys.12 035015

[19]Seddon E A,Clarke J A,Dunning D J,Masciovecchio C,Milne C J,Parmigiani F,Rugg D,Spence J C H,Thompson J C H,Ueda K,Vinko S M,Wark J S,Wurth W 2017 Rep.Prog.Phys.80 115901

[20]Protopapas M,Keitel C H,Knight P L 1997 Rep.Prog.Phys.60 389

[21]Zhou Z Y,Yuan J M 2008 Phys.Rev.A 77 063411

[22]Cui X,Li S Y,Guo F M,Tian Y Y,Chen J G,Zeng S L,Yang Y J 2015 Acta Phys.Sin.64 043201(in Chinese)[崔鑫,李苏宇,郭福明,田原野,陈基根,曾思良,杨玉军2015物理学报64 043201]

[23]Bachau H,Budriga O,Dondera M,Florescu V 2013 Centr.Euro.J.Phys.11 1091

[24]Ebadi H,Keitel C H,Hatsagortsyan K Z 2011 Phys.Rev.A 83 063418

[25]Tian Y Y,Guo F M,Zeng S L,Yang Y J 2013 Acta Phys.Sin.62 113201(in Chinese)[田原野,郭福明,曾思良,杨玉军2013物理学报62 113201]

[26]Pont M,Gavrila M 1990 Phys.Rev.Lett.65 2362

[27]Gavrila M 2002 J.Phys.B:At.Mol.Opt.Phys.35 R147

[28]Wei S S,Li S Y,Guo F M,Yang Y J,Wang B 2013 Phys.Rev.A 87 063418

[29]Hara T,Inubushi Y,Katayama T,Sato T,Tanaka H,Tanaka T,Togashi T,Togawa K,Tono K,Yabashi M,Ishikawa T 2013 Nat.Commun.4 2919

[30]Petralia A,Anania M P,Artioli M,Bacci A,Bellaveglia M,Carpanese M,Chiadroni E,Cianchi A,Ciocci F,Dattoli G,Giovenale D,Di Palma E,Di Pirro G P,Ferrario M,Giannessi L 2015 Phys.Rev.Lett.115 014801

[31]Wu Y K,Yan J,Hao H,Li J Y,Mikhailov S F,Popov V G,Vinokurov N A,Huang S,Wu J 2015 Phys.Rev.Lett.115 184801

[32]Couprie M E 2014 J.Elect.Spectro.Relat.Phenom.196 3

[33]Lutman A A,Coffee R,Ding Y,Huang Z,Krzywinski J,Maxwell T,Messerschmidt M,Nuhn H D 2013 Phys.Rev.Lett.110 134801

[34]Allaria E,Bencivenga F,Borghes R,Capotondi F,Castronovo D,Charalambous P,Danailov M B 2013 Nat.Commun.4 2476

[35]Schwartz E,Schwartz S 2015 Opt.Express 23 7471

[36]Perrella C,Light P S,Anstie J D,Stace T M,Benabid F,Luiten A N 2013 Phys.Rev.A 87 013818

[37]Ffushitani M,Hikosaka M,Matsuda A,Endo T,Shigemasa E,Nagasono M,Sato T,Togashi T,Yabashi M,Ishikawa T,Hishikawa A 2013 Phys.Rev.A 88 063422

[38]Matsuoka L,Hasegawa S 2007 J.Opt.Soc.Am.B 24 2562

[39]Liu M,Guo Y C,Wang B B 2015 Chin.Phys.B 24 073201

[40]Antaris A L,Chen H,Cheng K,Sun Y,Hong G S,Qu C R,Diao S,Deng Z X,Hu X M,Zhang B,Zhang X D,Yaghi O K,Alamparambil Z R,Hong X C,Cheng Z,Dai H J 2016 Nat.Mater.15 235

[41]Yang Y J,Chen J G,Chi F P,Zhu Q R,Zhang H X,Sun J Z 2007 Chin.Phys.Lett.24 1537

[42]Song Y,Li S Y,Liu X S,Guo F M,Yang Y J 2013 Phys.Rev.A 88 053419

[43]Zhou Z Y,Chu S I 2011 Phys.Rev.A 83 013405

[44]Wang C C,Tian Y,Luo S,Roeterdink W G,Yang Y,Ding D,Okunishi M,Prümper P,Shimada K,Ueda K,Zhu R 2014 Phys.Rev.A 90 023405

[45]Tian Y Y,Li S Y,Wei S S,Guo F M,Zeng S L,Chen J G,Yang Y J 2014 Chin.Phys.B 23 053202

[46]Zhang D Y,Li Q Y,Guo F M,Yang Y J 2016 Acta Phys.Sin.65 223202(in Chinese)[张頔玉,李庆仪,郭福明,杨玉军2016物理学报65 223202]