多面体外接球半径的几种求法
2018-03-25庞建荣
庞建荣

摘 要:与多面体的外接球有关的计算问题在近年高考试题中屡见不鲜,本文就长方体、正方体及棱锥的外接球有关问题,给出了几种常见的解法。
关键词:多面体外接球;半径问题;解法
《普通高中数学课程标准》中对立体几何初步的学习提出了基本要求:“在立体几何初步部分,学生将先从对空间几何体的整体观察入手,认识空间图形;再以长方体为载体,直观认识和理解空间点、线、面的位置关系;┅ ┅。”由此可见,长方体模型是学习立体几何的基础,掌握长方体模型,对于学生理解立体几何的有关问题起着非常重要的作用。有关外接球的立体几何问题是近年各省高考试题的热点之一,这与学生的空间想象能力以及化归能力有关,本文通过近年来部分高考试题中外接球的问题谈几种解法。
一、直接法
(一)与长方体的外接球的有关问题
例1、一个长方体的各顶点均在同一球面上,且一个顶点上的三条棱长分别为1,2,3,则此球的表面积为_______。
解析:关键是求出球的半径,因为长方体内接于球,所以它的体对角线正好是球的直径。长方体体对角线长为■,故球的表面积为14π。
(二)与棱柱的外接球的有关问题
例2、一个六棱柱的底面是正六边形,其侧棱垂直于底面,已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为■,底面周长为3,则这个球的体积为_______。
解析:设正六棱柱的底面边长为x,高为h,则有6x=36×■x2h=■, ∴x=■h=■
∴正六棱柱的底面园的半径r=■,球心到底面的距离d=■
∴外接球的半径R=■=1, ∴V球=■
小结:以上题型是运用公式R2=r2+d2求球半径的,该公式是求球半径的常用公式。
二、构造法
(一)构造正方体
例3、若三棱锥的三条侧棱两两垂直,且侧棱长均为■,则其外接球的表面积是__________
解析:此题用一般解法,需要作出棱锥的高,然后再设出球心,利用直角三角形计算球的半径,而作为填空题,我们更想使用较为便捷的方法,所以三条侧棱两两垂直,使我们很快联想到长方体的一个角,马上构造长方体,且侧棱长均相等,所以可构造正方体模型,那么三棱锥的外接球的直径即为正方体的对角线长,故所求表面积是9π。
例4、四面体的所有棱长都为■,四个顶点在同一球面上,则此球的表面积为 ( )
A.3π B.4π C.3■π D.6π
解析:一般解法,需设出球心,作出高线,构造直角三角形,再计算球的半径.在此,由于所有棱长都相等,我们联想只有正方体中有这么多相等的线段,所以构造一个正方体,再寻找棱长相等的四面体,由此可求得正方体的棱长为1,体对角线为■,从而外接球的直径也为■,所以此球的表面积便可求得,故选A.
(二)构造长方体
例5、已知点A、B、C、D在同一球面上,AB⊥平面BCD,BC⊥DC,若AB=6,AC=2■,AD=8,则B、C两点间的球面距离是_________
解析:首先通过联想可构造如下的长方体,于是AD为球的直径,O为球心,OB=OC=4为半径,要求B、C两点间的球面距离,只要求出∠BOC即可,在Rt△ABC中,求出BC=4,所以∠BOC=60°,故B、C两点间的球面距离是■π。
三、确定球心位置法
例6、在矩形ABCD中,AB=4,BC=3,沿AC将矩形ABCD折成一个直二面角B-AC-D,则四面体ABCD的外接球的体积为( )
A.■π B.■π
C.■π D.■π
解析:设矩形对角线的交点为0,则由矩形对角线互相平分,可知OA=OB=OC=OD,
∴点O到四面体的四个顶点A、B、C、D的距离相等,即点O为四面体的外接球的球心,如图4所示。
∴外接球的半径R=OA=■π,故V球=■π,选C。
四、寻求轴截面圓半径法
例7、正四棱锥S-ABCD的底面边长和各侧棱长都为■,点S、A、B、C、D都在同一球面上,则此球的体积为____
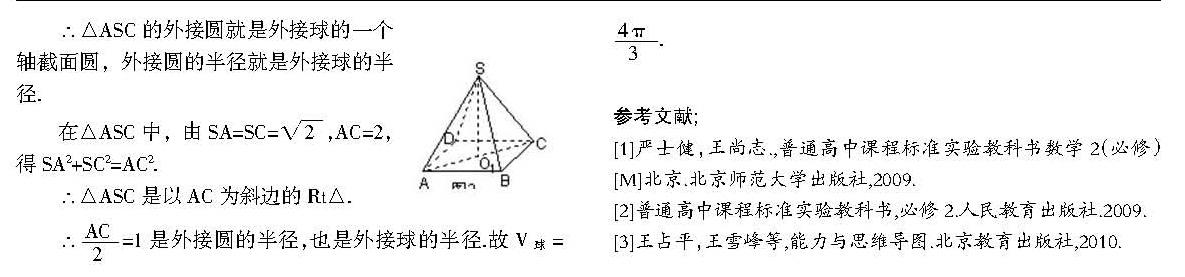
解析:根据题意,我们可以选择最佳角度找出含有正棱锥特征元素的外接球的一个轴截面圆,于是该圆的半径就是所求的外接球的半径.设正四棱锥的底面中心为O1,外接球的球心为O,如图5所示.
∴由球的截面的性质,可得OO1⊥平面ABCD.又SO1⊥平面ABCD
∴球心O必在SO1所在的直线上.
∴△ASC的外接圆就是外接球的一个轴截面圆,外接圆的半径就是外接球的半径.
在△ASC中,由SA=SC=■,AC=2,得SA2+SC2=AC2.
∴△ASC是以AC为斜边的Rt△.
∴■=1是外接圆的半径,也是外接球的半径.故V球=■.
参考文献;
[1]严士健,王尚志.,普通高中课程标准实验教科书数学2(必修) [M]北京.北京师范大学出版社,2009.
[2]普通高中课程标准实验教科书,必修2.人民教育出版社.2009.
[3]王占平,王雪峰等,能力与思维导图.北京教育出版社,2010.
