基于混沌优化极限学习机的库岸边坡变形预测
2018-03-25张志会
张志会
(国核电力规划设计研究院有限公司,北京 100095)
0 引 言
随着水资源开发的加速进行,水库及水电站被大量新建,不仅产生了大量电力资源,还有效提高了水资源的合理调配。受库区地质条件的影响,库区边坡的变形破坏和塌岸问题普遍存在,如柘溪水库上游1.5 km处发生大规模岸坡失稳;龟石水库上游6.5 km范围内共计发生了60余处规模不一的岸坡失稳[1]。许多学者对库区岸坡失稳研究取得了相应成果,杨妙帆等[2]结合库区勘察资料及水文条件,采用不平衡推力法分析了库区岸坡的稳定性,为后期治理提供了依据;宋丹青等[3]、尹云坤等[4]分析了水库蓄水对区内滑坡稳定性的影响,为类似水利工程提供了参考依据。上述研究虽取得了一定的成果,但未涉及库岸边坡的变形预测研究。为此,本文以锦屏水电站和三峡库区岸坡为实例,构建混沌优化的极限学习机模型,对岸坡变形进行预测,以判断其发展趋势,为库区灾害防治提供参考。
1 基本原理
1.1 极限学习机
极限学习机(ELM)是一种新型神经网络,具3层网络结构,即输入层、隐藏层和输出层。该模型较传统神经网络具有较大的优越性,主要体现在操作简单、泛化能力强及收敛速度快等方面,适用于解决岸坡变形预测问题。根据极限学习机的基本原理,可将其训练模型表示为
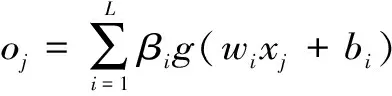
式中,oj为训练模型的第j个训练值;L为隐藏层神经元个数;βi为第i个隐层神经元与输出层间的连接权值;g(x)为激励函数;wi为输入层与第i个隐层神经元间的连接权值;xj为第j个输入样本;bi为第i个隐藏层神经元处的阈值。
根据网络训练,可得训练误差E,即
式中,N为训练样本个数;tj为第j个期望值。
若训练参数设置得当,训练值可零误差趋近于期望值,即
根据变换,可将上式转变为矩阵形式,即
Y=Hβ
式中,Y为输出矩阵;H为输入矩阵;β为权值矩阵。
在训练过程中,连接权值和阈值可随机给定,加之输入、输出矩阵为常数矩阵,进而极限学习机的训练过程可看作上式最小二乘解的求解过程。
1.2 参数优化过程
根据极限学习机的基本原理,在训练过程中,只需设置隐层神经元数和激励函数,但这2个参数的设置并未形成统一规范,多是由使用者的经验而定。为保证2个参数的最优化,本文提出利用逐步试算法确定最优隐层节点数和激励函数[5- 6]。
1.2.1 隐层神经元数
根据Kolmogorov定理,单隐层神经网络的隐层神经元数与其输入层神经元数存在如下关系
Ny=2Nr+1
式中,Ny为隐层神经元数;Nr为输入层神经元数。
在本文实例中,输入层神经元数设置为5,输出层神经元数设置为1,根据上式计算,得初始隐层神经元数为11。为搜寻最优隐层神经元数,以初始隐层神经元数为基础,将隐层神经元数的取值区间进行扩展,设置为8~14,并通过逐步试算法确定最优隐层神经元数。
1.2.2 激励函数
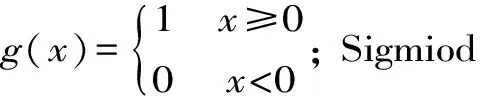
由于激励函数仅有3种类型,因此,也对3种激励函数的预测效果进行逐步试算,以确定最优激励函数。
1.2.3 混沌理论
根据上述,极限学习机虽具有较好的预测效果,但未考虑岸坡变形的混沌特性。因此,本文以混沌理论为基础,构建混沌优化极限学习机模型。
Lyapunov指数λ能很好评价变形序列的稳定性及发散程度。因此,将其最大值λmax作为岸坡变形序列是否具有混沌特性的评价指标。当λmax<0时,变形序列处于稳定状态,不具有混沌特性;当λmax=0时,变形序列处于临界状态,不能判断其是否具有混沌特性;当λmax>0时,变形序列处于不稳定状态,具有混沌特性。同时,由于Rosenstein算法[7]对噪声及数据长度等具有较好的鲁棒性,因此本文将其作为Lyapunov指数的求解方法。
当岸坡变形序列具有混沌特性时,利用坐标延迟法重构相空间,即将一维变形序列转变为m维的相空间。由于嵌入维数m和延迟时间τ对重构质量具有较大影响,为保证两者的有效性,本文采用Cao算法、自相关法分别确定2个参数。
1.2.4 优化过程
根据上述,将混沌优化ELM模型的优化过程分述如下:
(1)将隐层神经元数设置11,并逐步试算3种激励函数的预测效果,且以平均残差和平均相对误差为评价指标,确定最优激励函数。
(2)在确定最优激励函数的基础上,再对不同隐层神经元数的预测效果进行逐步试算,同样以平均残差和平均相对误差为评价指标,确定最优隐层神经元数。
(3)利用混沌理论实现变形序列的相空间重构,再利用参数优化后的极限学习机进行预测,进而实现混沌优化预测。
2 实例分析
2.1 工程概况
锦屏一级水电站进行了大量的岸坡开挖,最大开挖高度达500 m级,由于开挖卸荷作用,边坡变形明显。为掌握边坡变形情况,在施工过程中,布设了大量的变形监测点,地表监测点TP12-1的监测数据较为完整,将该监测点的变形数据作为本文预测模型的验证数据来源。根据现场监测,共获得21期监测数据,最大变形量达33.8 mm[8-9]。监测数据见图1。
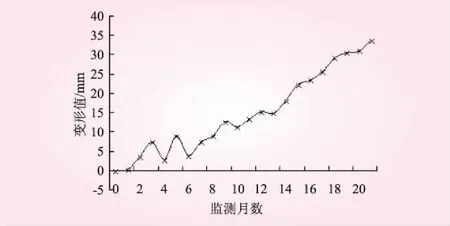
图1 监测数据
2.2 变形预测
根据前述,本文预测模型共有3个优化步骤,在各步骤中均以1~16周期为训练样本,17~21周期为验证样本,将各优化过程分述如下。
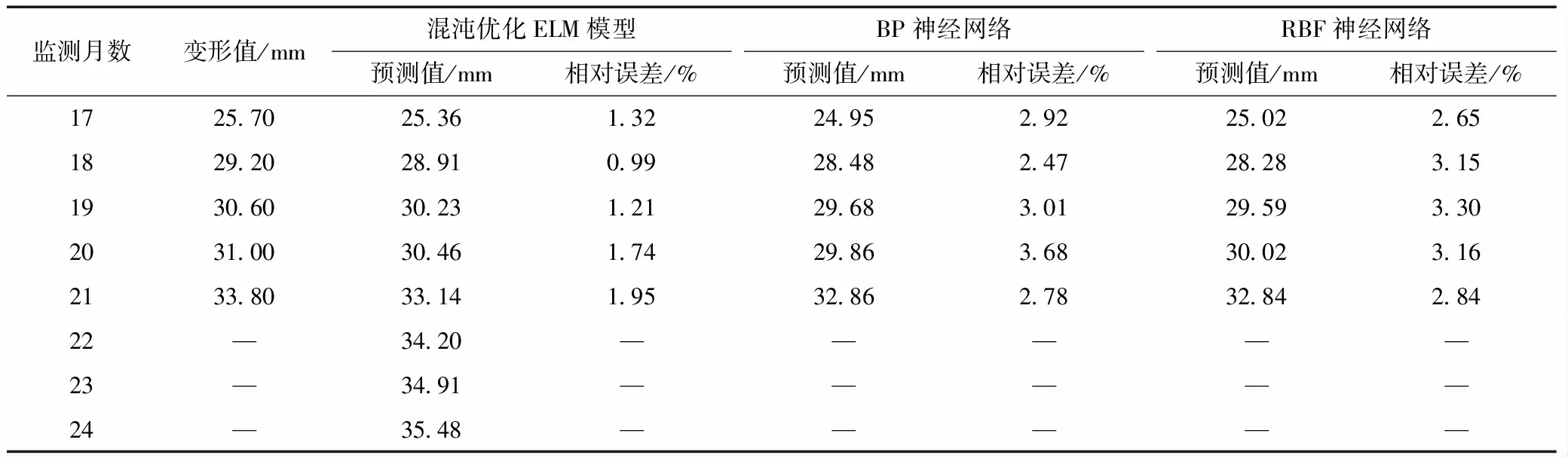
表3 不同预测模型的预测效果统计
2.2.1 激励函数优化
先将隐层节点数设置为11,对3种激励函数的预测效果进行逐步试算,结果见表1。由表1可知,不同激励函数的预测效果存在差异,Hardlim型激励函数的预测效果相对最优,其平均残差为0.9 mm,平均相对误差为2.98%, Sigmiod型与Sine型激励函数的预测效果相对次之。因此,确定激励函数为Hardlim型。
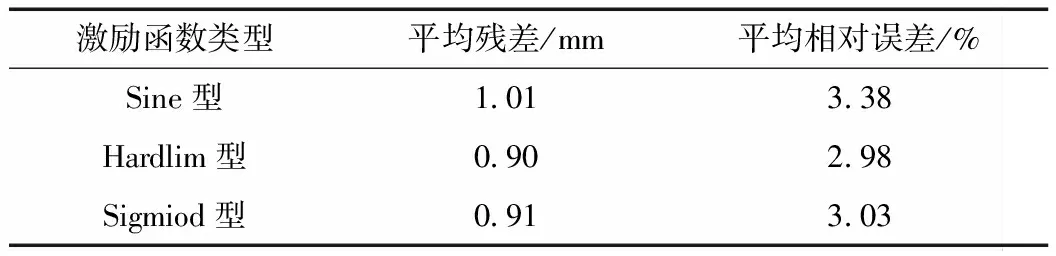
表1 不同激励函数的预测效果
2.2.2 隐层神经元数优化
根据隐层神经元的优化原理,对8~14的隐层神经元数进行逐步试算,结果见表2。对比不同隐层神经元数的预测效果可知,随着隐层神经元数的增加,预测效果先变优后变差,以隐层神经元数为12时的预测效果最优,说明隐层神经元数并非越多越好,存在最优神经元数。根据试算结果,确定隐层神经元数为12。
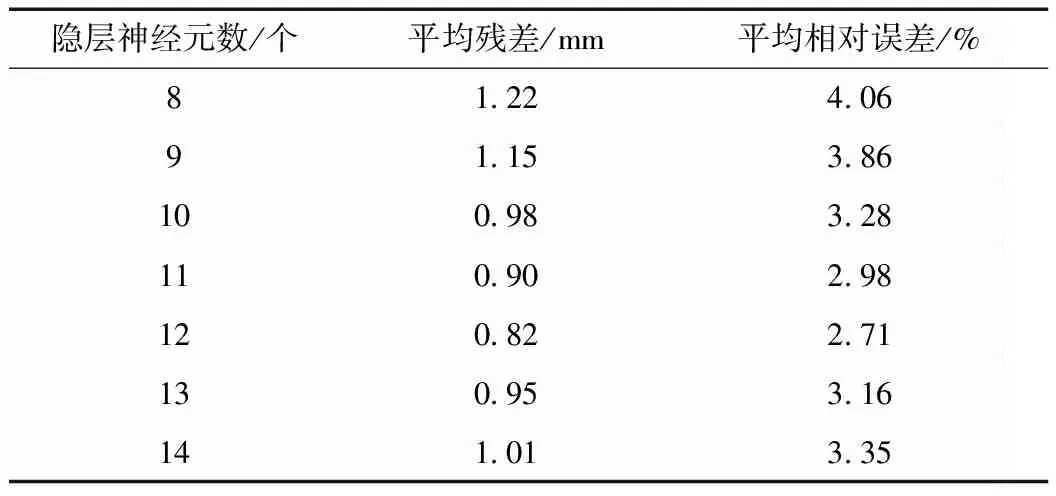
表2 不同隐层神经元数的预测效果
2.2.3 混沌理论优化
利用Rosenstein算法计算边坡变形序列的Lyapunov指数,得λmax=0.013>0,说明变形序列处于不稳定状态,具有混沌特性。因此,对岸坡变形序列进行空间重构,以实现混沌优化预测。为对比本文模型与传统神经网络的预测效果,再利用BP神经网络和RBF神经网络进行相应的变形预测,各预测模型的结果见表3。从表3可知,在相应验证节点处,混沌优化ELM模型的相对误差均小于2种传统神经网络的相对误差,说明本文预测模型具有更高的预测精度,验证了本文优化手段的有效性;混沌优化ELM模型的相对误差均值为1.44%,明显优于混沌理论优化前的2.71%,说明通过混沌理论优化,进一步提高了预测精度;22~24个月的外推预测可知,岸坡的变形量仍在进一步增加,建议对该边坡加强监测,并采取必要措施控制变形发展。
3 可靠性验证
上述实例虽得出本文预测模型具有较高预测精度,但单一实例难以验证预测模型的可靠性。因此,再引入1个验证实例,对混沌优化ELM模型的可靠性进行验证。
3.1 工程概况
三峡工程是我国重要的水利工程之一,其船闸是工程建设的重要组成部分[10-11]。在船闸修建过程中,形成了高陡边坡,鉴于该工程的重要性,对其变形进行了长期监测,共监测36个月。其中,BM10GP01和BM29GP02监测点的监测成果较为完善,因此,将2个监测点的变形数据作为可靠性验证的数据来源。2个监测点的变形曲线见图2。
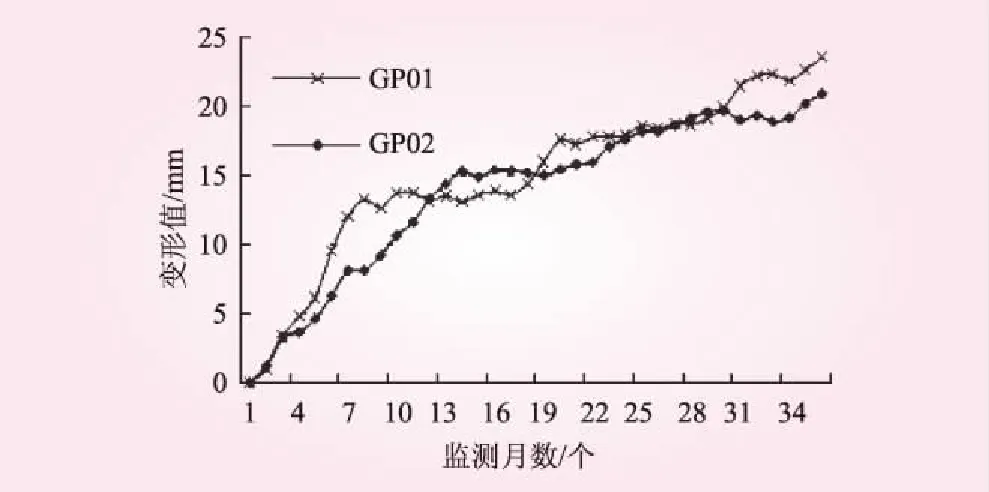
图2 监测变形
3.2 变形预测
类比前一实例的预测过程,也对可靠性验证实例的最优激励函数和隐层神经元数进行寻优。
3.2.1 激励函数优化
同理,先将隐层神经元数设置为11,得出3种激励函数的预测结果见表4。从表4可知,Sigmiod型激励函数的平均残差为0.68 mm,平均相对误差为3.01%,较其他2种激励函数具有更好的预测精度。因此,在可靠性验证实例中,确定激励函数为Sigmiod型。
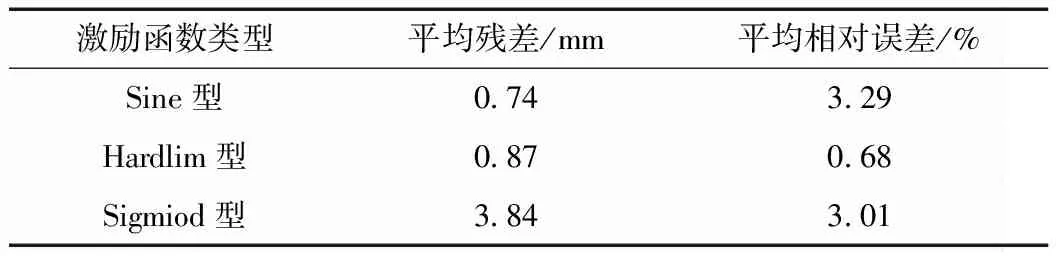
表4 可靠性验证实例的激励函数筛选
3.2.2 隐层神经元数优化
通过不同隐层神经元数的逐步试算,得到其预测结果见表5。在可靠性验证实例中,隐层神经元数为13时,具有最小的平均残差及相对误差,说明该神经元数的预测效果最优;同时,随着神经元数的增加,预测效果先变好再变差,且最优神经元数与传统公式确定的神经元数具有差异,验证了通过试算法确定最优隐层神经元数的必要性。根据试算结果,确定可靠性验证实例的隐层神经元数为12。
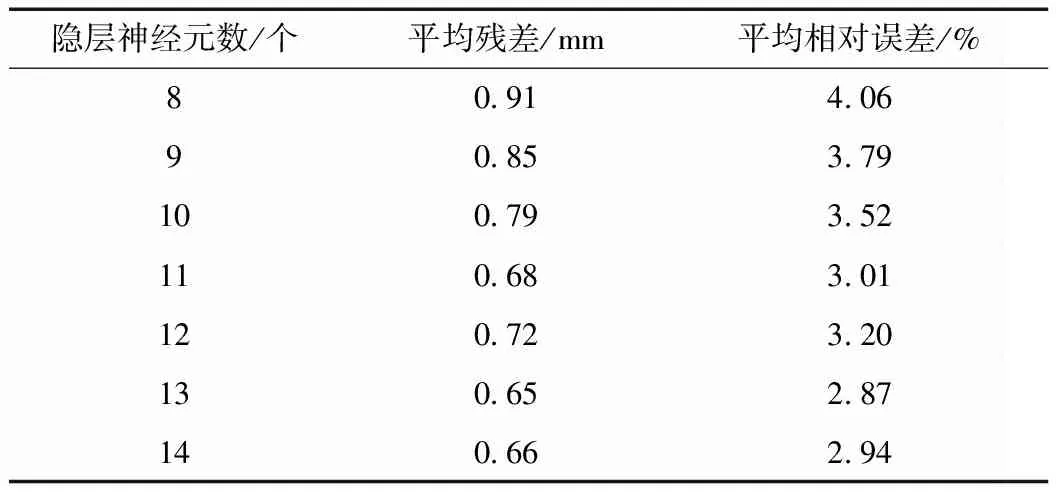
表5 可靠性验证实例的隐层神经元数筛选
对比2个实例的最优网络参数可知,最优激励函数和隐层神经元数与实例相关。因此,在极限学习机的应用过程中,有必要根据试算法确定不同实例的优化参数。
3.2.3 混沌理论优化
同理,也利用Rosenstein算法确定变形序列的Lyapunov指数,得到BM10GP01监测点的λmax=0.017>0,BM29GP02监测点的λmax=0.022>0,说明2个监测点的变形序列均具有混沌特性。因此,利用混沌理论进行优化预测,结果见表6。由表6可知,BM10GP01监测点的相对误差均值为1.67%,BM29GP02监测点为1.99%,2个监测点的预测效果均优于混沌理论优化前的预测效果,说明混沌理论能有效提高预测精度,验证了混沌优化ELM模型的可靠性;37~39个月的外推预测可知,监测点的变形仍将持续增加。
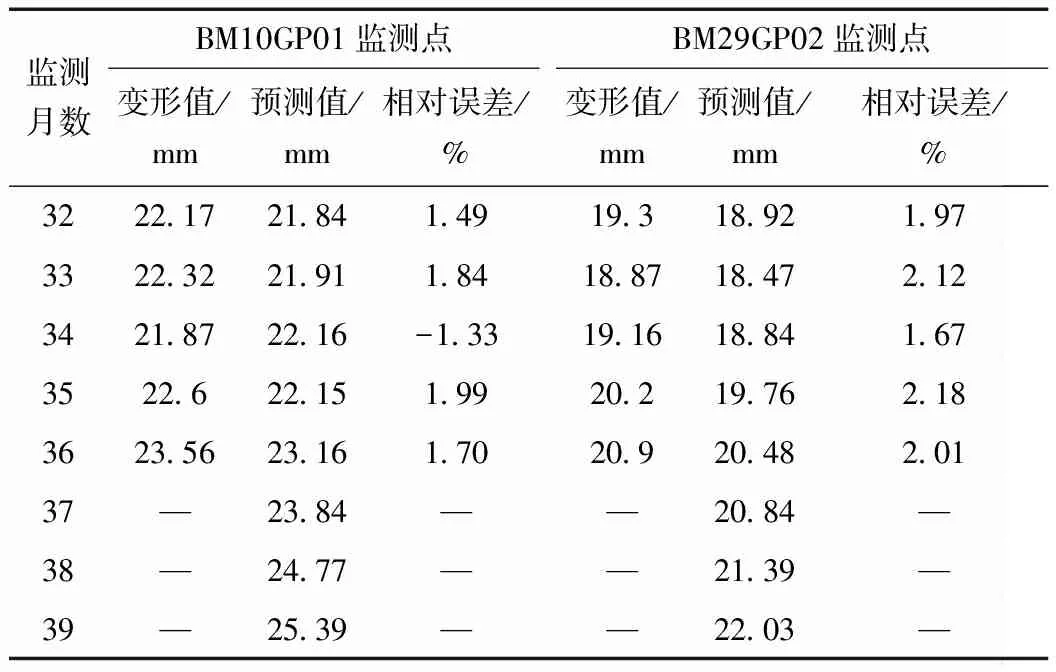
表6 混沌优化ELM模型的可靠性预测结果
综上,混沌优化ELM模型在2个实例中均具有较高的预测精度,验证了该模型的有效性和可靠性,可推广应用。
4 结 语
本文利用逐步试算法和混沌化理优化极限学习机的网络参数,构建了混沌优化ELM模型,通过实例分析,得出以下结论:
(1)逐步试算法可有效确定极限学习机的最优隐层神经元数和激励函数,且通过参数优化,能有效提高预测精度,但不同实例的最优网络参数具有差异,应针对具体实例进行相应的试算,以确定对应的优化参数。
(2)库区岸坡的变形序列具有混沌特性,且通过混沌理论的空间重构优化,进一步提高了预测精度,验证了混沌理论的优化效果。
(3)混沌优化ELM模型不仅具有较高的预测精度,还具有较好的泛化能力和可靠性,相较于传统神经网络具有更大优越性。
(4)库岸边坡所处的环境条件较为复杂,其变形具有显著的复杂性和非线性特点,本文提出的混沌优化ELM模型在库岸边坡的非线性预测中具有较好的适用性。
