填土表面倾斜的涵洞顶垂直土压力研究
2018-03-25贾德鹏李永刚周慧珍
贾德鹏,李永刚,周慧珍
(1.太原理工大学水利科学与工程学院,山西 太原 030024;2.太原理工大学图书馆,山西 太原 030024)
0 引 言
涵洞广泛应用于水利、土木和交通等行业当中,其顶部土压力是涵洞设计的重要依据。当前对涵洞土压力的研究只考虑涵洞顶部填土水平的情况,对填土表面倾斜的涵洞顶垂直土压力研究较少。1930年,Marston开始研究涵洞土压力[1];1948年,Spangler对沟埋式涵洞垂直土压力进行了理论论述[2];1981年,顾安全等分析了涵洞上覆填土的内外土柱之间的摩擦影响,并提出涵顶垂直土压力的弹性计算方法[3];1994年以后,国内外众多学者展开土拱效应对涵洞土压力影响的研究,以及通过各种方法减小涵洞土压力的探讨[4-11]。这些研究都是考虑涵洞上覆填土表面水平的情况,而实际工程中,土坝和路基下的涵洞大部分处于表面倾斜的填土边坡之下,边坡下涵洞顶部的填土高度沿轴向各不相同,涵洞各断面的上覆填土的压缩量不同,导致洞顶土压力不同于表面水平填土下涵洞的土压力。为此,本文对填土表面倾斜的边坡下涵洞土压力进行理论分析和有限元模拟,为工程设计提供参考。
1 计算思路
箱涵埋设在边坡填土之下,与填土表面水平的情况相比,除涵洞两侧填土的下拖作用之外,计算断面存在高填土侧和低填土侧的影响。鉴于此,边坡下涵洞顶部的垂直土压力可以从横(垂直涵洞轴线)、纵(平行于涵洞轴线)2个方向进行考虑:对土压力的横向分析可以借鉴填土表面水平的情况处理,纵向分析时可以从高、低侧填土对计算断面的下拽和上托作用入手进行研究。
2 边坡下涵洞土压力横向计算
考虑常用的钢筋混凝土箱形涵洞和刚性地基,取涵顶填土为无粘性砂土,横向计算模型见图1。图中,H为涵洞顶部填土高度,He为等沉面高度,H1′为等沉面以上填土高度,B为箱涵外宽和外高。涵洞顶部填土高度H较小时,洞顶上方土体Ⅰ(内土柱)的沉降小于其两侧土体Ⅱ(外土柱)的沉降,即内外土柱有沉降差;随填土高度增大,内外土柱的摩擦使两者的沉降差逐渐减小,此沉降差为0时的洞顶填土高度即为初始等沉面高度He0;填土高度大于初始等沉面高度之后,等沉面高度He随填土高度H的不同而变化。等沉面以下内外土柱的沉降差形成的摩擦导致了涵顶的横向附加土压力。
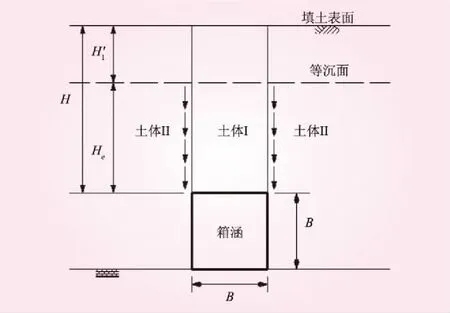
图1 横向计算模型
2.1 H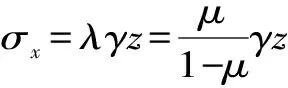
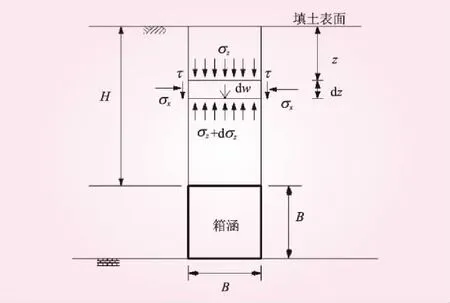
图2 H根据图2中水平微元列竖向力的平衡可得
dw+Bσz-B(σz+dσz)+2τdz=0
(1)
整理得
(2)
z=0时,σz=0微分方程(2)对应的解为
(3)
z=H的垂直土压力就是涵洞顶部土压力,即
(4)
此值除以涵顶的自由土柱压力γH,可得涵顶的横向垂直土压力系数K1为
(5)
2.2 H≥He 0情况
H≥He0的计算简图见图3。图3中,q为等沉面以上的平均垂直土压力,则
q=γH1′
(6)
在等沉面以下土体Ⅰ的某一深度z处,取水平微分单元,列其竖向力的平衡方程,其结果同式(2)。由z=0时,σz=q=γH1′的初始条件确定其解为
(7)
z=He时的垂直土压力就是涵顶平均垂直土压力,即
(8)
相应的涵顶横向土压力系数K1为
(9)
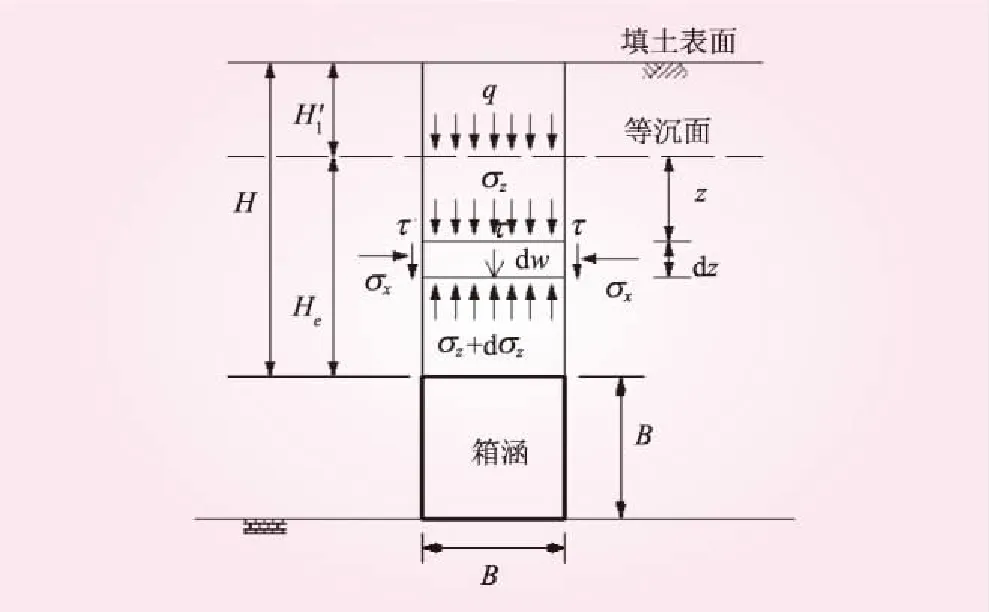
图3 H≥He0计算示意
2.3 等沉面高度计算
H≥He0时,令土体Ⅱ及涵洞两侧土体的压缩量之和等于土体Ⅰ的压缩量(忽略涵洞压缩量),可得等沉面高度He。根据图3,在等沉面以下z处,土体Ⅰ的平均垂直土压力由式(7)可得,并记作σ1,土体Ⅱ的平均垂直土压力σ2=γ(H1′+z),两者的垂直土压力平均值σ3=(σ1+σ2)/2。利用弹性理论,计算土体Ⅰ的压缩量Δ1为
(10)
土体Ⅱ和涵洞两侧土体的压缩量Δ2为
(11)
式中,E为土体压缩模量。
由变形协调条件Δ1=Δ2得He。H1′=0、q=0时的等沉面高度就是初始等沉面高度He0,H≤He0时,没有等沉面。利用数值积分可得到不同填土高度的等沉面高度He。
3 边坡下涵洞土压力纵向计算
沿涵洞纵向看,箱涵顶部的填土高度各不相同,相应的沉降和压缩量各不一样,填土高度大压缩量大,其沉降大;填土高度小压缩量小,其沉降小。高填土对相邻的低填土有向下的摩擦作用,低填土对相邻的高填土有上托作用。沿箱涵轴向取单位长度L=1为计算段,建立边坡下涵洞土压力纵向计算模型,高填土侧土体对计算段土柱的向下摩擦力Q2减去低填土侧土体对计算段土柱的向上摩擦力Q1,即为计算段涵顶纵向的附加土压力。纵向计算模型见图4。
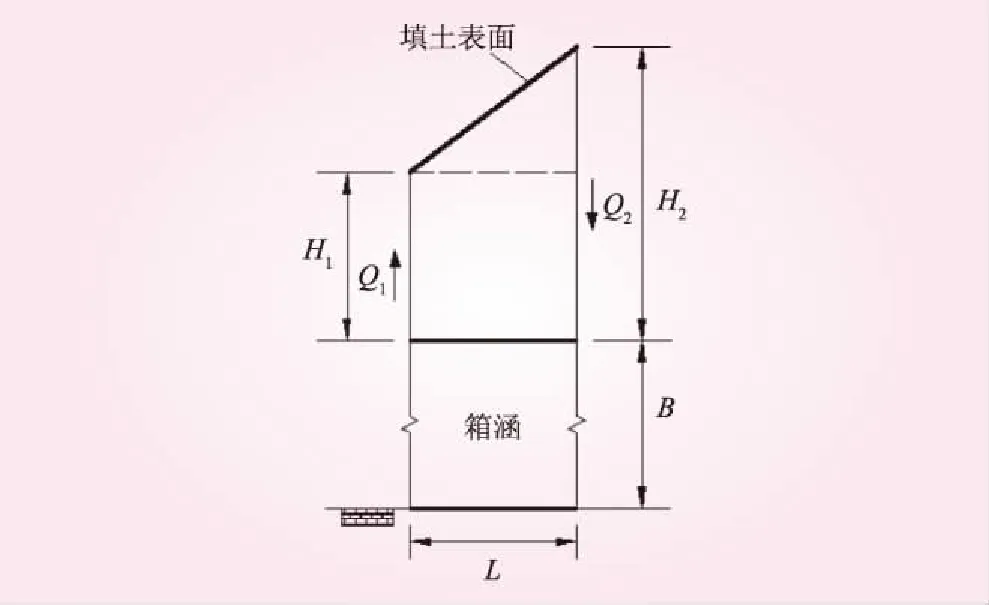
图4 纵向计算模型
取涵顶填土的边坡系数为m,计算段中心的填土高度H,计算段低填土侧填土高度H1=H-1/2m,计算段高填土侧填土高度H2=H+1/2m。H2断面和H1断面对计算段的摩擦力代数和就是涵洞纵向附加土压力,即
(12)
纵向附加土压力除以土柱压力γH即得涵顶纵向土压力系数K2,即
(13)
4 边坡下涵洞土压力(系数)计算
边坡下涵洞的土压力系数就是横、纵两向土压力系数之和,即
K=K1+K2
(14)
边坡下涵洞纵向高、低填土侧对计算段的下拽和上托作用形成边坡效应,产生了纵向土压力系数K2,使填土表面倾斜的边坡下涵洞的土压力大于表面水平填土的涵洞土压力,其土压力系数较填土表面水平的涵洞土压力系数增大了K2。K2与填土的侧压力系数λ、内摩擦角φ正切成正比,与边坡系数m成反比。现取泊松比μ=0.22,计算所得K2的变化见表1。从表1可知,坡度陡、内摩擦角大,则K2大,边坡效应使涵洞土压力较自由场土柱压力增大0~40%,边坡系数m=∞为涵顶填土表面水平状况。经计算,φ=30°时,水平填土涵洞的K1最大值为1.46,而m=0.5的K2=0.32,K2/K1=22%,即边坡下涵洞土压力较水平填土涵洞土压力增大0~22%。
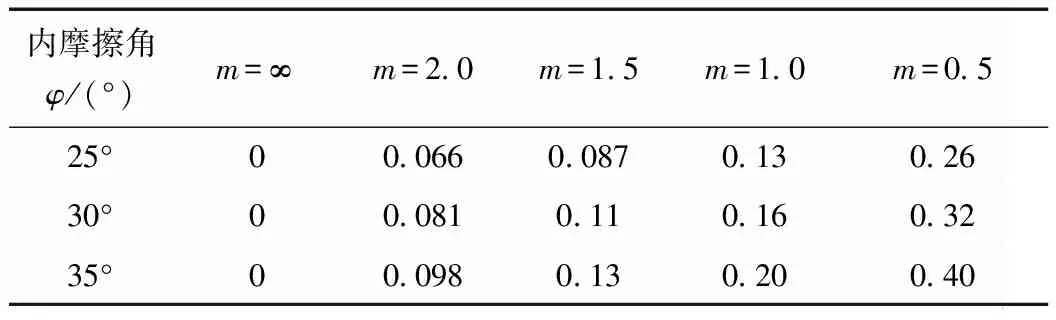
表1 不同边坡系数m下的纵向土压力系数K2
为验证理论分析,建立边坡下涵洞ANSYS有限元三维计算模型进行弹性计算,有限元模型见图5,含有96 254个节点和19 080个单元。模型采用刚性地基上的混凝土方涵,外宽、外高B=4 m,混凝土材料为C25,密度ρ=2 400 kg/m3,采用Solid65单元模拟。填土为无粘性砂土,泊松比μ=0.22,内摩擦角φ=30°,重度γ=18.5 kN/m3,采用Solid95单元模拟。填土边坡系数m=1.0,边坡最大填土高度H=15B,在涵洞与填土之间设置接触面,接触面采用TARGE170和CONTA174单元,摩擦系数取0.3。模型底部节点位移为0,侧面节点水平位移为0。有限元模拟所得涵洞顶土压力系数与理论计算的土压力系数比较见图6。从图6可知,两者的变化趋势一致,相对差平均值为6.9%。

图5 边坡下涵洞有限元计算网格

图6 土压力系数变化(m=1.0)
5 结 语
本文通过理论分析和数值模拟对填土表面倾斜的涵洞顶垂直土压力进行分析,并与填土表面水平的涵洞垂直土压力进行比较,得出以下结论:
(1)涵洞顶部填土高度相同情况下,填土表面倾斜的涵洞土压力大于填土表面水平的涵洞土压力,土坝和路堤下涵洞土压力系数需适当增大。
(2)边坡效应形成的纵向土压力系数,随填土泊松比、内摩擦角的增加而增大,随边坡系数的增大而减小。
(3)边坡效应使涵洞顶垂直土压力较自由场土柱压力增大0~40%,填土表面倾斜的涵洞顶垂直土压力较填土表面水平涵洞增大0~22%。
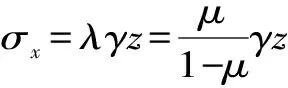

图2 H 根据图2中水平微元列竖向力的平衡可得 dw+Bσz-B(σz+dσz)+2τdz=0 (1) 整理得 (2) z=0时,σz=0微分方程(2)对应的解为 (3) z=H的垂直土压力就是涵洞顶部土压力,即 (4) 此值除以涵顶的自由土柱压力γH,可得涵顶的横向垂直土压力系数K1为 (5) H≥He0的计算简图见图3。图3中,q为等沉面以上的平均垂直土压力,则 q=γH1′ (6) 在等沉面以下土体Ⅰ的某一深度z处,取水平微分单元,列其竖向力的平衡方程,其结果同式(2)。由z=0时,σz=q=γH1′的初始条件确定其解为 (7) z=He时的垂直土压力就是涵顶平均垂直土压力,即 (8) 相应的涵顶横向土压力系数K1为 (9) 图3 H≥He0计算示意 H≥He0时,令土体Ⅱ及涵洞两侧土体的压缩量之和等于土体Ⅰ的压缩量(忽略涵洞压缩量),可得等沉面高度He。根据图3,在等沉面以下z处,土体Ⅰ的平均垂直土压力由式(7)可得,并记作σ1,土体Ⅱ的平均垂直土压力σ2=γ(H1′+z),两者的垂直土压力平均值σ3=(σ1+σ2)/2。利用弹性理论,计算土体Ⅰ的压缩量Δ1为 (10) 土体Ⅱ和涵洞两侧土体的压缩量Δ2为 (11) 式中,E为土体压缩模量。 由变形协调条件Δ1=Δ2得He。H1′=0、q=0时的等沉面高度就是初始等沉面高度He0,H≤He0时,没有等沉面。利用数值积分可得到不同填土高度的等沉面高度He。 沿涵洞纵向看,箱涵顶部的填土高度各不相同,相应的沉降和压缩量各不一样,填土高度大压缩量大,其沉降大;填土高度小压缩量小,其沉降小。高填土对相邻的低填土有向下的摩擦作用,低填土对相邻的高填土有上托作用。沿箱涵轴向取单位长度L=1为计算段,建立边坡下涵洞土压力纵向计算模型,高填土侧土体对计算段土柱的向下摩擦力Q2减去低填土侧土体对计算段土柱的向上摩擦力Q1,即为计算段涵顶纵向的附加土压力。纵向计算模型见图4。 图4 纵向计算模型 取涵顶填土的边坡系数为m,计算段中心的填土高度H,计算段低填土侧填土高度H1=H-1/2m,计算段高填土侧填土高度H2=H+1/2m。H2断面和H1断面对计算段的摩擦力代数和就是涵洞纵向附加土压力,即 (12) 纵向附加土压力除以土柱压力γH即得涵顶纵向土压力系数K2,即 (13) 边坡下涵洞的土压力系数就是横、纵两向土压力系数之和,即 K=K1+K2 (14) 边坡下涵洞纵向高、低填土侧对计算段的下拽和上托作用形成边坡效应,产生了纵向土压力系数K2,使填土表面倾斜的边坡下涵洞的土压力大于表面水平填土的涵洞土压力,其土压力系数较填土表面水平的涵洞土压力系数增大了K2。K2与填土的侧压力系数λ、内摩擦角φ正切成正比,与边坡系数m成反比。现取泊松比μ=0.22,计算所得K2的变化见表1。从表1可知,坡度陡、内摩擦角大,则K2大,边坡效应使涵洞土压力较自由场土柱压力增大0~40%,边坡系数m=∞为涵顶填土表面水平状况。经计算,φ=30°时,水平填土涵洞的K1最大值为1.46,而m=0.5的K2=0.32,K2/K1=22%,即边坡下涵洞土压力较水平填土涵洞土压力增大0~22%。 表1 不同边坡系数m下的纵向土压力系数K2 为验证理论分析,建立边坡下涵洞ANSYS有限元三维计算模型进行弹性计算,有限元模型见图5,含有96 254个节点和19 080个单元。模型采用刚性地基上的混凝土方涵,外宽、外高B=4 m,混凝土材料为C25,密度ρ=2 400 kg/m3,采用Solid65单元模拟。填土为无粘性砂土,泊松比μ=0.22,内摩擦角φ=30°,重度γ=18.5 kN/m3,采用Solid95单元模拟。填土边坡系数m=1.0,边坡最大填土高度H=15B,在涵洞与填土之间设置接触面,接触面采用TARGE170和CONTA174单元,摩擦系数取0.3。模型底部节点位移为0,侧面节点水平位移为0。有限元模拟所得涵洞顶土压力系数与理论计算的土压力系数比较见图6。从图6可知,两者的变化趋势一致,相对差平均值为6.9%。 图5 边坡下涵洞有限元计算网格 图6 土压力系数变化(m=1.0) 本文通过理论分析和数值模拟对填土表面倾斜的涵洞顶垂直土压力进行分析,并与填土表面水平的涵洞垂直土压力进行比较,得出以下结论: (1)涵洞顶部填土高度相同情况下,填土表面倾斜的涵洞土压力大于填土表面水平的涵洞土压力,土坝和路堤下涵洞土压力系数需适当增大。 (2)边坡效应形成的纵向土压力系数,随填土泊松比、内摩擦角的增加而增大,随边坡系数的增大而减小。 (3)边坡效应使涵洞顶垂直土压力较自由场土柱压力增大0~40%,填土表面倾斜的涵洞顶垂直土压力较填土表面水平涵洞增大0~22%。2.2 H≥He 0情况

2.3 等沉面高度计算
3 边坡下涵洞土压力纵向计算

4 边坡下涵洞土压力(系数)计算



5 结 语
