刚体卫星相平面控制闭环系统稳定性分析*

陈志华，解永春,2,3

0 引 言

随着现代控制理论的发展和计算机在卫星控制系统中的应用，可以采用更复杂的开关控制律来满足控制系统的性能要求.文献[1]介绍了一种大小推力联合控制的相平面控制律，通常称为相平面控制方法.相平面控制主要适用于中低轨道卫星入轨后消除姿态偏差、速率阻尼、姿态捕获、姿态机动、正常轨道运行期间和变轨发动机工作期间的姿态稳定，也可用于航天器的返回控制和交会对接.此外，早期美国阿波罗飞船姿态控制[2]、美国火星着陆器姿态控制[3]以及日本隼鸟号小行星探测器姿态控制[4]都使用了相平面控制方法.

然而，相平面控制方法设计参数较多，且基本依赖于工程师的经验和试凑.针对这些不足，解永春等[5]将黄金分割自适应控制思想引入相平面控制设计，克服了现有相平面控制设计参数需要试凑的弊端，最终提出了基于特征模型的相平面自适应控制方法[6-8].该方法进一步发展了相平面控制方法，为相平面控制的工程应用提供理论依据.基于特征模型的相平面自适应控制方法已经在我国“神舟八号”、“神舟九号”飞船与“天宫一号”目标飞行器的交会对平移靠拢段控制中得到了成功应用，取得了预期的控制效果[8].

众所周知，相平面控制属于非线性控制，其既属于切换控制，又属于采样控制.考虑到现代航天器通常具有高阶、非线性、时变性和不确定性等因素，因此航天器相平面控制闭环系统通常属于含有不确定性，控制时延的时变非线性切换采样系统，如“神舟八号”飞船交会对接靠拢段控制[6，8].

相平面控制中的切换属于状态依赖切换，故当系统状态穿越分区边界时，会出现控制不能随着闭环系统状态所在分区及时更新的情况，也有文献[9-10]称之为控制与系统不匹配(mode mismatch)问题，这种情况相当于引入了不超过一个采样周期的控制延时.此外，当一个采样控制周期的控制已经确定时，在该采样控制周期内还可能出现控制开关切换的情况，即在该采样控制周期内发动机开机一定长度后再关机.这种在一个采样周期内发生控制切换的情况使得闭环系统的稳定性分析问题变得更加复杂[10].目前，关于切换控制系统和采样控制系统的稳定性研究已经取得了不少结果[11-12].然而，针对同时存在控制切换和周期采样的系统，其稳定性研究结果还很少[10].因此，针对相平面控制系统的稳定性，尚没有可借鉴的成熟方法来研究，文献[13]也将相平面控制的稳定性分析问题列为公开难题.

根据研究相平面控制系统稳定性的已有结果[14-16]来看，相平面控制系统稳定性分析方法主要分为时域法和频域法两类.频域法主要有数值计算描述函数法[14-15]、圆判据以及Popov判据等.数值计算描述函数的方法可以得出相平面控制律的近似描述函数，但描述函数法本身是一种近似方法，因此使用该方法进行稳定性分析的可信度难以保证.此外，当相平面控制律参数发生改变时，需要重新计算相平面控制环节的描述函数，即该方法难以有效地分析控制参数时变的控制系统稳定性.文献[16]首先通过Siljak环路变换将相平面航天器控制系统转换成Lure型系统，进而采用圆判据和Popov判据分析航天器相平面控制系统的绝对稳定性.但文献[16]考虑的相平面控制是连续的，不存在固定周期采样问题，也就不涉及采样周期内的切换问题，故文献[16]的方法不能直接用来分析本文相平面控制系统的稳定性.

时域法主要包括计算机仿真方法[6，17]、Lyapunov方法以及相平面分析方法.计算机仿真方法即通过计算机随机打靶仿真来判断闭环控制系统在统计意义下是否稳定，且该种方法已经在实际航天器控制系统的稳定性分析中得到了广泛应用[17].但要指出的是，计算机随机打靶仿真中对于系统是否稳定的判别基本依赖于工程师的经验.此外，由于计算机仿真时长有限，使得难以利用计算机时域仿真来分析非线性时变控制系统的长时间行为，如稳定性.同样，由于计算机仿真次数是有限的，故难以分析系统对于参数不确定性的鲁棒稳定性.总之，利用计算机仿真分析控制系统稳定性尚缺乏严格的理论依据.

由于相平面控制具有非线性和混杂特性，难以直接利用Lyapunov方法分析相平面控制系统的稳定性.据我们所知，目前尚未见到基于Lyapunov方法分析相平面控制系统稳定性的报道.相平面控制系统属于切换采样系统，据我们所知，针对一般切换采样系统的稳定性尚没有普适的分析方法.针对一类特殊的采样切换线性系统，文献[10]采用Lyapunov方法分析其稳定性，但需要附加很强的前提假设条件，故文献[10]的分析方法难以用于相平面控制系统.

相平面分析方法[18]是分析低阶非线性控制系统稳定性的有效方法，该方法通过直接分析二阶系统的轨线行为来判断系统的稳定性，具有几何直观的优点.然而，该方法难以用于高阶控制系统的稳定性分析.相平面分析方法在二阶复杂控制系统稳定性研究中得到了广泛应用，如文献[19]通过相平面分析方法研究带有输入延时的二阶滑模控制系统的稳定性.但据我们所知，目前尚未见到基于相平面分析方法研究相平面控制系统稳定性的文献.

在本文中，首先对相平面控制律进行适当简化，并选取刚体卫星作为被控对象，最终对所组成的闭环控制系统的稳定性进行研究.具体来说，采用相平面分析方法对闭环控制系统轨线进行定量估计，证明闭环控制系统存在特定的稳态区域.同样，采用相平面分析方法定量估计闭环控制系统的轨线，证明当相平面控制律参数满足一定条件时，闭环控制系统的所有轨线都是一致最终有界的.此外，还给出了闭环控制系统轨线从任意初始状态到达稳态区域的时间估算公式.

总结来说，本文主要贡献体现在以下3个方面：

1)对航天器控制系统中常用的相平面控制律进行简化改进，但保留了其中的状态依赖切换控制和固定周期采样的特点(这两个特点是导致闭环系统稳定性难以分析的主要因素)，得到一种简化相平面控制律；

2)以简化相平面控制律为基础，以刚体卫星姿态动力学模型作为被控对象，采用相平面分析方法定量估计闭环控制系统轨线的方法，证明闭环控制系统存在特定的稳态区域，且稳态区域完全由相平面控制参数决定；

3)基于相平面分析方法定量估计闭环控制系统轨线的思想，给出了从任意初值出发的相平面闭环控制系统的轨线一致最终有界的充分条件.此外，还给出了从任意初值出发的闭环控制系统轨线到达稳态区域的时间估算公式，为后续研究相平面控制系统稳定性以及改进设计提供初步理论依据.

1 问题描述

1.1 简化相平面控制律

在文献[1，8]给出的相平面控制律基础上，不失一般性，通过合并原相平面控制中的部分分区得到简化相平面控制律，如图1所示.其中，相平面控制律参数由表1给出，相平面控制律的具体计算公式由表2给出.

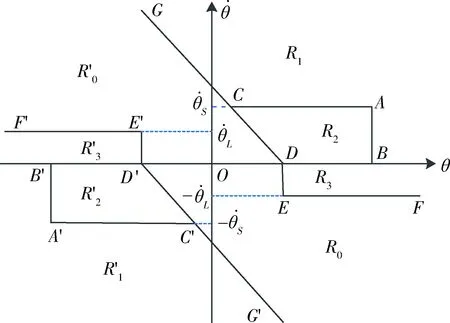
图1 简化相平面控制律相平面分区示意图Fig.1 The zones divided in the simplified phase-plane control

注1.简化相平面控制律保留了根据系统状态所在分区进行控制切换和固定周期采样这两个因素，这些因素直接导致了难以分析相平面控制系统稳定性.

设采样控制周期为T，根据控制系统的状态采样点θ(t0+kT)，k=1,2,…所在区域，简化相平面控制律u(t)，t∈[t0,∞)设计如下：

表1 相平面控制律相关参数Tab.1 Related parameters of the simplified phase-plane control law

表2 相平面控制计算公式Tab.2 The calculation formulas of the phase-plane control

计算得到右半平面开关线GCD方程为

类似地，左半平面开关线G′C′D′方程为

其中，开关线斜率为

(1)

为了突出相平面控制律中状态依赖切换和固定周期采样因素，我们以刚体卫星作为被控对象，进而研究姿态控制闭环系统的稳定性.

1.2 被控对象

考虑刚体卫星的姿态控制，由简化相平面控制和刚体卫星单轴动力学组成的闭环控制系统可以表示成：

(2)

其中，x(t)∈R1表示姿态角，I>0为刚体卫星单轴惯量参数，u(t)为简化相平面控制，其具体形式由表2 给出.

(3)

其中，σ表示简化相平面控制由于状态分区产生的切换信号，uσ表示对应于切换信号σ的控制.

1.3 相关定义

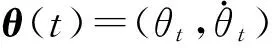
定义2[21-22].(一致最终有界,uniform ultimate boundedness)给定初始时刻t0，称系统从初始状态θ0=θ(t0)出发的解θ(t):[t0,+∞)→R2是一致最终有界的；如果存在一个C集μ(不依赖t0)和非负数T(θ0,μ)，使得

θ(t)∈μ,∀t≥t0+T(θ0,μ)

(4)

进一步，如果式(4)对于任意θ0∈R2成立，则称系统的解是全局一致最终有界的.

注2．C集[22]指的是内部包含原点的紧凸集.

2 预备引理

为了推导本文主要结果，在本节给出3个预备引理，先给出3个假设条件.

假设1.大、小推力发动机分别提供的力矩幅值FM与Fm满足：Fm=0.25FM.

假设2.采样控制周期T=160 ms，推力器最小喷气长度Tmin=50 ms.

假设3.若闭环控制系统状态的采样点位于直线(段)GCD，DE，EF，G′C′D′，D′E′，E′F′上，则进行关机控制.

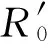
2.1 稳态区域存在性

(5)

则存在区域(称为稳态区域)

(6)

具有下述3个性质：

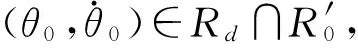
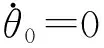
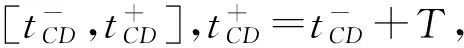
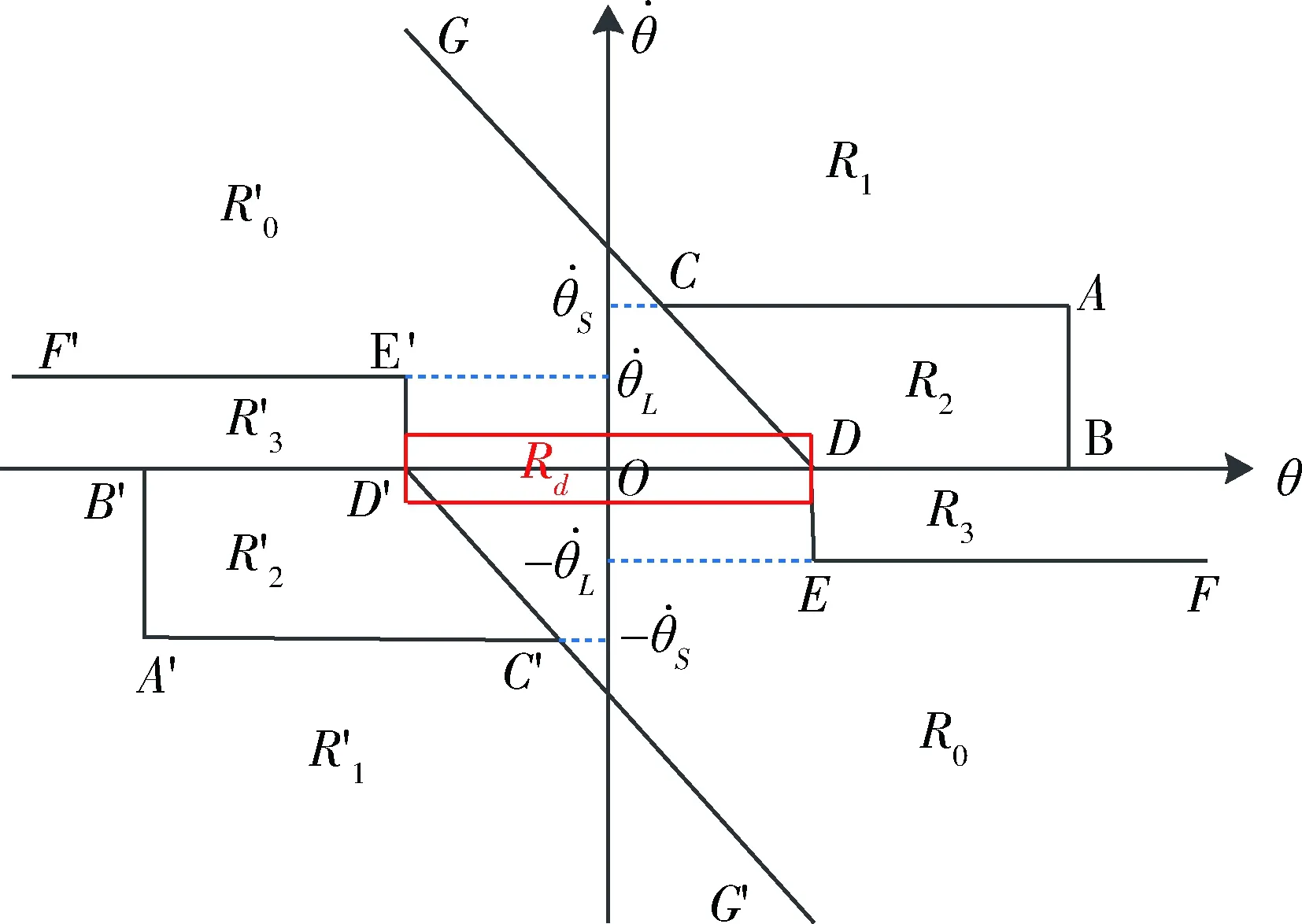
图2 闭环控制系统稳态区域Rd示意图Fig.2 The zone Rd of stable states of the phase-plane control close-loop system

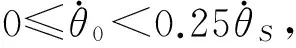
其中，Tcross表示从t1到穿越横轴θ=0的历时，即

根据条件(5)可知：KX≤1/(T+3.5Tmin)，因此

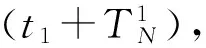
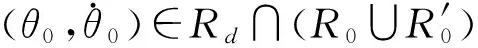
其中，Tcross表示从t1到穿越横轴θ=0的历时，即

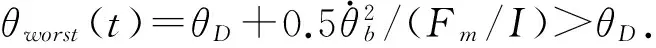
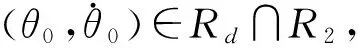
再证明闭环系统轨线从Rd中最多穿出一次，且经过有限时间后会再次进入Rd，并将保持在Rd内.

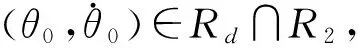
记第1次采样时刻为t1，而第1次喷气长度

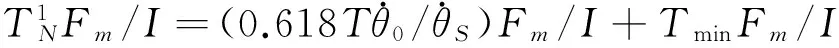
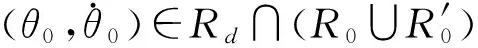
在第1次喷气结束时刻，闭环系统轨线的横坐标θ(t1+TN)相对θD的右偏移量

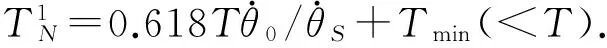
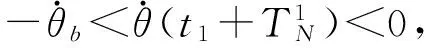
(7)

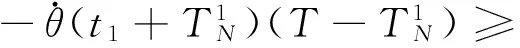
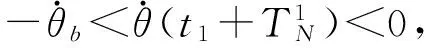
(8)

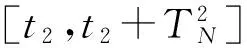
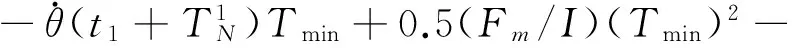
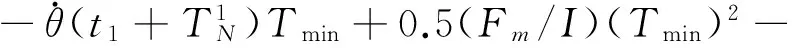
因此，可以推出

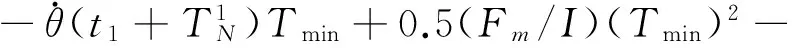
另一方面，根据条件(7)可知：

因此，

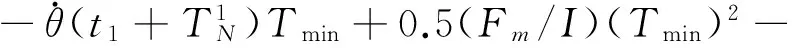
根据式(8)可知，第2次喷气必将使得闭环系统轨线穿越线段DE.

而从闭环系统轨线纵坐标来看，第2次喷气完成后，闭环系统轨线在纵向的增量

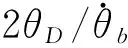
记第3次采样时刻为t3，显然t3=t2+T，在第3次喷气开始时刻t3，按最坏情况计算，闭环系统轨线在横向的坐标最小为

(9)

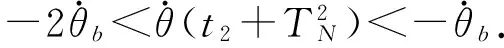
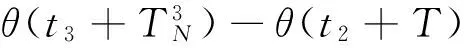
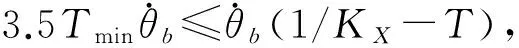
(10)

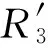
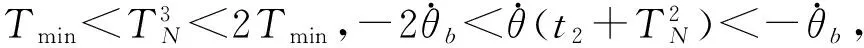
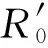
2.2 临界区域存在性

本节给出的引理2将证明存在具有下述性质的区域：一旦闭环系统轨线进入该区域，则闭环系统轨线将在有限时间内进入稳态区域Rd.

(11)

定义区域(称为临界区域)，如图3所示：

(12)

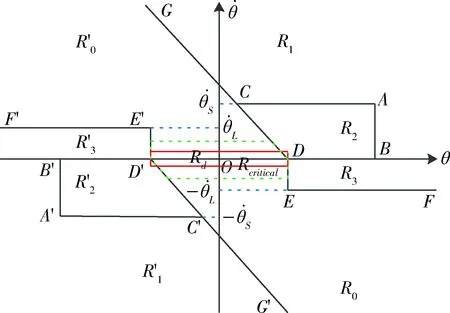
图3 相平面控制闭环系统临界区域Rcritical示意图Fig.3 The critical zone Rd of the phase-plane control closed-loop system

证明.由题设条件可知：

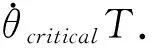
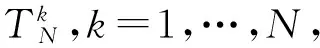
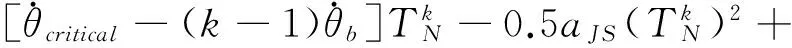
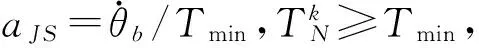
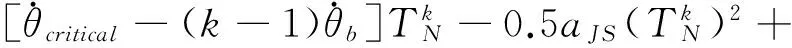
其中，k=1,…,N.

故在这不超过N次的喷气过程中，闭环系统轨线向右偏移量不超过

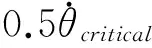
故闭环系统轨线穿越CD后向右的偏移量不超过

.

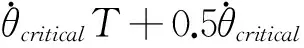
(13)

(14)

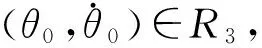
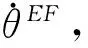
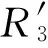
2.3 稳态区域有限时间可达性

对于任意给定初值，闭环系统的轨线可在有限时间内进入稳态区域Rd，下述引理3证明了这点.

(15)

(16)

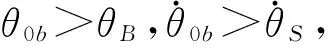
图4 闭环控制系统的初值状态限定区域ΩFig.4 The considered zone Ω of the initial values of the phase-plane control closed-loop system

当闭环系统轨线经过EF穿出R3区时，按保守计算，闭环系统轨线的向右横向偏移量必不超过

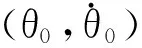
t1+t2+t3+max(t4,t5)

时间后，则闭环系统轨线必将进入Ω区域.

t1+t2+t3+max(t4,t5)

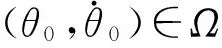
(17)

若|θc1|≤θD，则闭环系统轨线将进入Rd区，此后闭环系统轨线的运行情况已在引理1中讨论过.

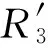
(18)

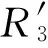
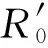
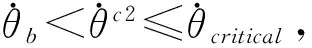
图5 闭环控制系统典型轨迹运行情况Fig.5 The representative trajectory of the phase-plane control system

若θc2≤θD，则闭环系统轨线将从R2区穿越CD进入Rd区，此后情况已在引理1中讨论过.

假设点N位于直线EF上，即闭环系统轨线穿越EF进入R0区，则根据R2和R3区的控制可知：闭环系统轨线在PN段的运行时间tPN，大于闭环系统轨线在MP段的运行时间tMP，即tPN>tMP.因此，闭环系统轨线在tPN时间内的横向位移增量大于DP，这与N位于直线EF上相矛盾.

故闭环系统轨线只能从DE进入R0区，而不会穿越EF进入R0区.

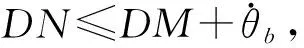
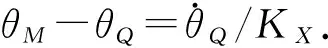
而根据R2区控制可知，闭环系统轨线在QM段运行期间的每个喷气控制周期内的纵向位移量不小于(Fm/I)Tmin.

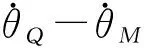
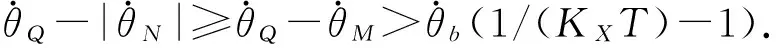
(19)

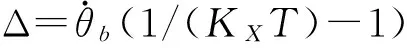
(20)

同样，按保守计算，每圈的环绕时间不超过

至此，证明了闭环系统轨线在有限时间内进入Rcritical区.再根据引理2可知，经过有限时间后，闭环系统轨线将进入Rd.

对于任意给定初值，为了估算从给定初值出发的闭环系统轨线到达稳态区域所用时间，基于引理1-3，我们提出下述引理4.

2.4 可达时间计算

(21)

Tf=T1+T2+T3+T4+T5

(22)

后，闭环系统轨线将进入Rd，并将一直保持在Rd内.

证明.图6给出闭环控制系统轨线运行全过程中依次经过的区域：

图6 闭环控制系统轨线运行各阶段示意图
Fig.6 The overall phases traversed by the trajectory of the phase-plane control closed-loop system

图7 闭环控制系统轨线依次经过区域示意图Fig.7 The zones traversed by the trajectory of the phase-plane control closed-loop system in sequence

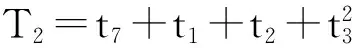
RL

(23)

同样根据引理3证明可知，一旦闭环系统轨线进入RL区，按最坏情况计算，则经过不超过T3=(Ncircle+1)Tcircle时间后，闭环系统轨线将进入临界区Rcritical内.

再根据引理2可知，经过不超过T4=t6时间后，闭环系统轨线将进入Rd区.

因此，按最坏情况计算，闭环系统轨线到达时间稳态区域Rd的时间不会超过

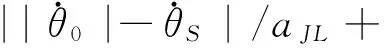
(24)

注5．当把感兴趣的初值范围限定在Ω区时，则T1=0，即Tf=T2+T3+T4+T5.

3 主要结果

根据第2节中引理1、引理2和引理4，即可证明闭环系统的一致最终有界性，具体由下述定理1给出.

(25)

根据引理1，引理2和引理4即可证明定理1，不再详细给出.

4 仿真验证

选取刚体卫星俯仰姿态控制为例进行仿真研究，具体仿真参数由表3给出.

表3 仿真参数Tab.3 Simulation parameters

取仿真总时间1 000 s，计算可知初值状态限定区域Ω=[-2,2]×[-2,2]，单位分别为(°)和/((°)/s).

仿真结果如图9所示，根据定理1可得闭环系统轨线到达稳态区域的时间为Testimate=1247.822 4 s.而由图9(b)和(c)可知，闭环系统轨线到达稳态区域的实际时间约为Treal=151.203 4 s.

图8 闭环系统数值仿真结果γ=3.2Fig.8 Simulation results of the phase-plane control closed-loop system with the initial value (2,2) when γ=3.2

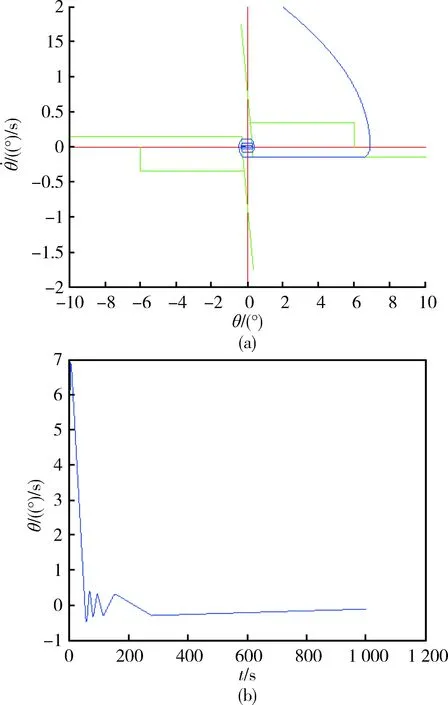
图9 闭环系统数值仿真结果γ=16Fig.9 Simulation results of the phase-plane control closed-loop system with the initial value (2,2) when γ=16

5 结 论

本文研究了航天器姿态相平面控制系统稳定性分析这一难题.首先提出一种简化相平面控制律，进而分析刚体卫星相平面控制闭环系统的稳定性.针对刚体卫星相平面控制闭环系统，首先证明闭环系统存在稳态区域的事实.进而基于相平面分析方法定量估计闭环控制系统的轨线，给出保证闭环控制系统轨线全局一致最终有界的充分条件，且该条件以关于相平面控制参数的不等式形式给出.同时，还给出闭环控制系统从任意初值到达稳态所用时间的估算公式.

所得结果为分析相平面控制系统稳定性提供了初步理论依据，也为相平面控制设计提供了初步指导准则.

后续研究中将针对一般的时变非线性航天器对象，考虑三轴惯量耦合及大角度姿态运动学自身的耦合特性、系统参数不确定性、控制与测量延时、外部扰动和测量噪声等因素，研究航天器相平面控制系统的鲁棒稳定性.

[1] 屠善澄.卫星姿态动力学与控制[M].北京: 宇航出版社, 2001:440-455.

[2] WIDNALL W S．Lunar module digital autopilot[J].Journal of Spacecraft and Rockets, 1971, 8(1): 56-62.

[3] CALHOUN P C, QUEEN E M.Entry vehicle control system design for the Mars science laboratory[J].Journal of Spacecraft and Rockets, 2006, 43(2): 324-329.

[4] KUBOTA T, OTSUKI M, HASHIMOTO T, et al.Touchdown dynamics for sampling in Hayabusa mission[C]//Proceedings of the 2006 AIAA/AAS Astrodynamics Specialist Conference and Exhibit.Keystone.Colorado: AIAA, 2006:1-12.

[5] 解永春, 吴宏鑫.黄金分割在自适应鲁棒控制器设计中的应用[J].自动化学报, 1992, 18(2): 177-185.

XIE Y C, WU H X.The application of the golden section in adaptive robust controller design[J].Acta Automatica Sinica, 1992, 18(2): 177-185.

[6] 解永春, 张昊, 胡军等.神舟飞船交会对接自动控制系统设计[J].中国科学: 技术科学, 2014, 44(1): 12-19.

XIE Y C, ZHANG H, HU J, et al.Automatic control system design of Shenzhou spacecraft for rendezvous and docking (in Chinese)[J].Scientia Sinica Technologica, 2014, 44(1): 12-19.

[7] 解永春, 胡军.基于特征模型的智能自适应控制方法在交会对接中的应用[J].系统科学与数学, 2013, 33(9): 1017-1023.

XIE Y C, HU J.The application of the intelligent adaptive control method based on characteristic model in rendezvous and docking[J].Journal of Systems Science and Mathematical Sciences, 2013, 33(9): 1017-1023.

[8] 解永春, 胡军, 吴宏鑫等.一种基于特征模型的相平面自适应控制方法[P].中国:CN201310108763.3, 2013-10-10.

[9] MA D, ZHAO J.Stabilization of networked switched linear systems: an asynchronous switching delay system approach[J].Systems & Control Letters, 2015, 77: 46-54.

[10] WAKAIKI M, YAMAMOTO Y.Stability analysis of sampled-data switched systems with quantization[J].Automatica, 2016, 69: 157-168.

[11] LIN H, ANTSAKLIS P J.Stability and stabilizability of switched linear systems: a survey of recent results[J].IEEE Transactions on Automatic Control, 2009, 54(2): 308-322.

[12] HETEL L, FITER C, OMRAN H, et al.Recent developments on the stability of systems with aperiodic sampling: An overview[J].Automatica, 2017, 76: 309-335.

[13] “10000个科学难题”信息科学编委会.10000个科学难题(信息科学卷) [M].北京: 科学出版社, 2011: 735-737.

[14] 张国琪, 刘洁, 董文强等.基于描述函数法的相平面喷气姿态控制的稳定性分析[J].空间控制技术与应用, 2015, 41(1): 15-20.

ZHANG G Q, LIU J, DONG W Q, et al.Stability analysis of phase-plane jet attitudes control system using the describing function method[J].Aerospace Control and Application, 2015, 41(1): 15-20.

[15] HATTIS P D, PENCHUK A N, KUBIAK E T.A frequency domain stability analysis of a phase plane control system[J].Journal of Guidance Control and Dynamics, 1985, 8(1): 50-55.

[16] JANG J W, PLUMMER M, BEDROSSIAN N, et al.Absolute stability analysis of a phase plane controlled spacecraft [R].Washington D.C., AIAA, 2010: 1-13.

[17] 吴宏鑫.工程实际中的控制理论和方法的研究与展望[J].控制理论与应用, 2014, 31(12): 1626-1631.

WU H X.Research and prospect on the control theory and method in the engineering[J].Control Theory and Applications, 2014, 31(12): 1626-1631.

[18] 高为炳.非线性控制系统导论[M].北京: 科学出版社, 1991:36-45.

[19] LEVAGGI L, PUNTA E.Analysis of a second-order sliding-mode algorithm in presence of input delays[J].IEEE Transactions on Automatic Control, 2006, 51(8): 1325-1332.

[20] LI H T, WANG Y Z.On reachability and controllability of switched Boolean control networks[J].Automatica, 2012, 48(11): 2917-2922.

[21] (美)哈里尔著, 朱义胜, 董辉, 李作洲译.非线性系统(第三版)[M].北京: 电子工业出版社, 2011: 112-113.

[22] DILDA V, JUNGERS M, CASTELAN E B.Uniform ultimate boundedness analysis and synthesis for linear systems with dead-zone in the actuators[J].International Journal of Robust and Nonlinear Control, 2015, 25(14): 2502-2514.