基于区域平均燃料消耗的推力器配置问题

王 敏，王思野

0 引 言

以推力器为执行机构的反作用控制系统，由于其对各种飞行任务较强的适应性，成为了航天器系统构成中及其重要的分系统，其性能的好坏直接影响到整个控制器的使命[1].由于推力器相对飞行器是固定安装的，其产生的推力矢量和控制力矩矢量仅取决于推力器安装的位置和倾角，所以单个推力器产生的控制量在本体系中的方向是固定的.一般航天器会安装多个推力器，通过其作用的组合来实现任意的合控制力和力矩，这种组合就是推力器的控制指令分配问题.

推力器的配置一般是指飞行器上配备的所有推力器的数量、推力大小、安装位置和指向等[1].将每个推力器在本体系三轴方向产生的力和力矩分量作为一个列向量，由配置中所有推力器列向量组成的矩阵，就称为推力器的配置矩阵.它包含了配置中推力器的安装位置和指向等信息.推力器的配置一旦确定，其性能的好坏将直接影响控制算法的精度、燃耗等性能指标，从而影响到控制任务的顺利执行.故推力器配置的性能分析对于控制任务设计阶段不同配置的性能比较和选择以及配置的进一步优化设计来说都具有重要意义.

以往对推力器配置的性能分析主要集中在配置的控制能力分析[2-4]，以及配置对于推力器故障情况的冗余度分析等方面[4-6].配置的控制能力分析是配置能否完成任务的基本保障，而对冗余度的分析则反映了配置在推力器故障情况下的可靠性.对于一个给定的任务，不同的推力器配置采用相同的指令分配算法，其得到的燃料消耗也是不同的.文献[7]提出一个性能指标，用来衡量同样任务同样指令分配方法情况下，不同推力器配置造成的燃料消耗差异，即推力器配置燃料消耗的相对大小，但是在控制矢量的分布函数选择方面有待改进，并且对于六维控制任务采用拆分为力和力矩单独评价的方式.本文提出区域平均燃料消耗指标，对于三维和六维的控制任务，都能通过积分给出控制任务总体平均燃料消耗的度量方法，从而知道推力器配置的优化设计.

1 问题描述

以燃料消耗为代价函数的控制指令分配问题如下：

ming=cΤt，s.t.At=u，t≥0

(1)

其中c=[c1c2，…，cN]T，cN为第N台推力器单位工作时间消耗的推进剂量；t=[t1t2，…，tN]T，tN代表第n台推力器的开机工作时长.tN为待求解变量，非负约束(N个)表征推力器只能产生单向推力.

在实际控制任务中，推力器配置已定，轨道和姿态闭环控制过程中，不同的控制律产生的不同控制指令序列和不同的控制指令分配算法会导致不同的推进剂消耗.而在方案设计论证阶段，根据任务需求，在控制指令相对确定的情况下，不同的推力器配置则会产生不同的推进剂消耗.通过提出一个指标，来反映不同推力器配置阵针对控制指令区域合集的燃料消耗水平，则是本文的研究目的所在.

若要反映控制指令的空间分布在不同推力器配置下的性能，首先需要获得反映控制指令分布的倾向，在空间中可用概率密度函数来进行度量.但是实际的控制指令根据闭环的测算、反馈进行调整的，因此很难获得这种针对不同任务的控制指令分布函数.但是，假设在一定的控制区域内，控制指令不可预见，即完全随机.对于同一个推力器配置阵，应用控制区域内随机的控制指令，经控制指令分配后即可求解区域内的平均燃料消耗水平.

2 区域平均燃料消耗指标

为了保证归一化的控制指令的随机性，球面矢量选择应服从均匀分布，以单位球面上一点对应的控制指令u=[uxuyuz]T为例，在球体坐标系中有[ux=cosθsinφ,uy=sinθsinφ,uz=cosφ]，其中φ∈[-π/2,π/2]，θ∈[-π,π]为矢量u的俯仰角和方位角.由于球面微元面积为A=sinφdφdθ，可以看出球面上的矢量点与俯仰角非线性关系，是sinφ的函数，所以从均匀分布的俯仰角φ和方位角θ选取得到的矢量u并不服从均匀分布，矢量分布会集中在球面的两极，从而无法表征出随机控制指令分布.因此我们令γ=cosφ，得到dγ=sinφdφ，并改写控制指令矢量u为

(2)

其中θ∈[-π,π]，γ∈[-1,1].若θ和γ服从均匀分布，则控制指令u服从均匀分布.由此得到区域平均燃料消耗指标定义如下：

(2)

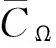
实际上，一组控制指令u对应多个可行解里的其中一组基矩阵B，不同的u对应不同的B.因此，可看成一种映射B=[b1(θ,γ)b2(θ,γ)b3(θ,γ)]T.这时燃料消耗g可表示为：

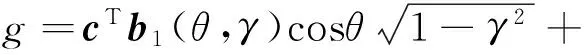
由于控制指令u的随机性，很难获得上述基矩阵B关于θ和γ的解析表达式.因此，采取分段积分的方式来逼近求得平均燃料消耗的积分值，即离散化积分区间进行概率平均求和，由于积分变量θ和γ独立，因此分割区间的选取可以分别进行，假设将方位角θ和γ按h等分，等分的份数决定积分的准确性，同时会影响积分的运算复杂度.

前文的分析是基于球体的三维坐标系，平均燃料消耗可以直接映射到三维位置或姿态控制任务的情况，这时控制矢量u为三维推力矢量或者三维力矩矢量.在需要进行六维轨道和姿态同时控制的情况下，控制矢量u=[uF(θF,γF)uM(θM,γM)]T.其中，uF为三轴推力矢量，uM为三维力矩矢量.由于控制指令的随机性，可以认为控制力矢量和控制力矩矢量是完全独立的，可以通过球面坐标的四重积分获得六维控制指令区域平均燃料消耗指标计算公式如下：

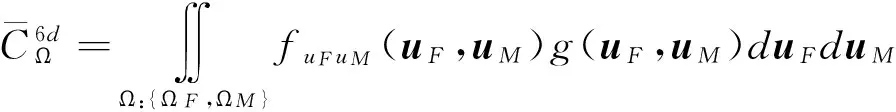
其中ΩF和ΩM为相应力和力矩控制矢量分布区域，轨道和姿态同时控制所产生的单次推进最小燃料消耗g(θF,θM,γF,γM)是如下线性规划问题的解：

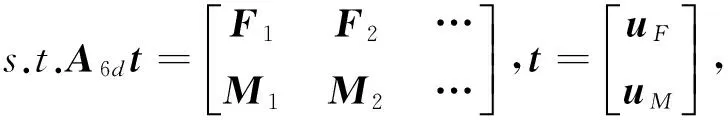
(3)

其中A6d代表六维推力器配置阵.

3 算例分析和优化思路

3.1 算例分析

以三维姿态控制为例进行分析，六维控制可以照此进行计算和分析，仅计算过程会相对复杂，这里不再赘述.现有6个推理器配置阵A1，A2，A3，A4，A5和A6如表1～6所示，推力器和力矩为归一化后的值.可以看出，推力器配置通过A+B的发动机配对使用消除力的作用，产生纯力矩进行三维姿态控制.不同的安装位置使得配置阵的力矩的矢量方向有所不同，如图1～6所示,验证比较在同一个控制指令区域的燃料消耗.

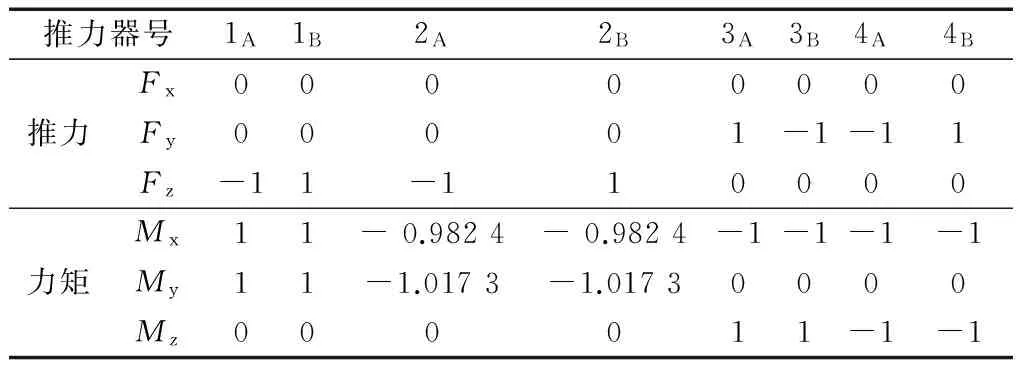
表1 推力器配置A1Tab.1 Thruster configuration A1

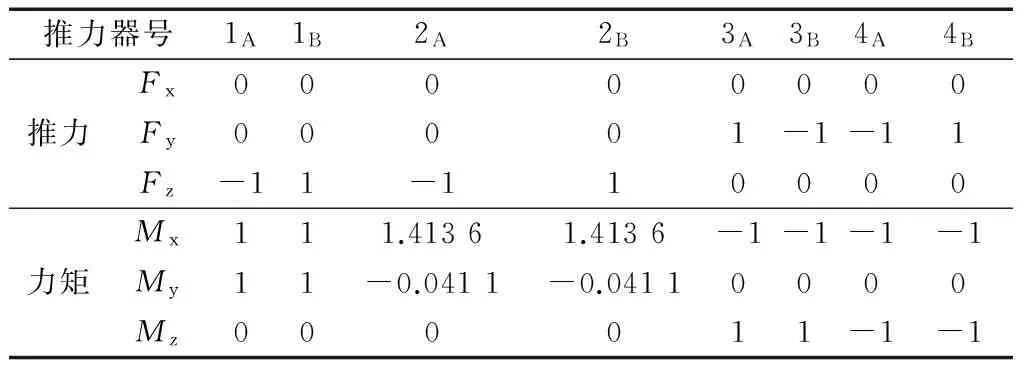
表2 推力器配置A2Tab.2 Thruster configuration table A2

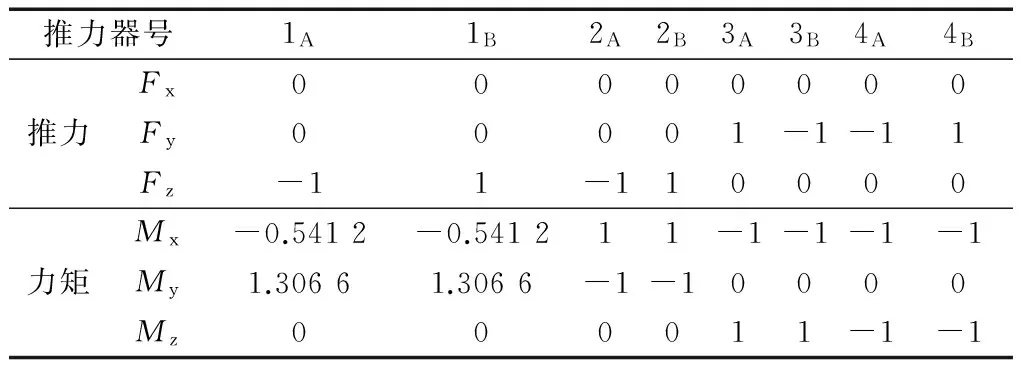
表3 推力器配置A3Tab.3 Thruster configuration table A3

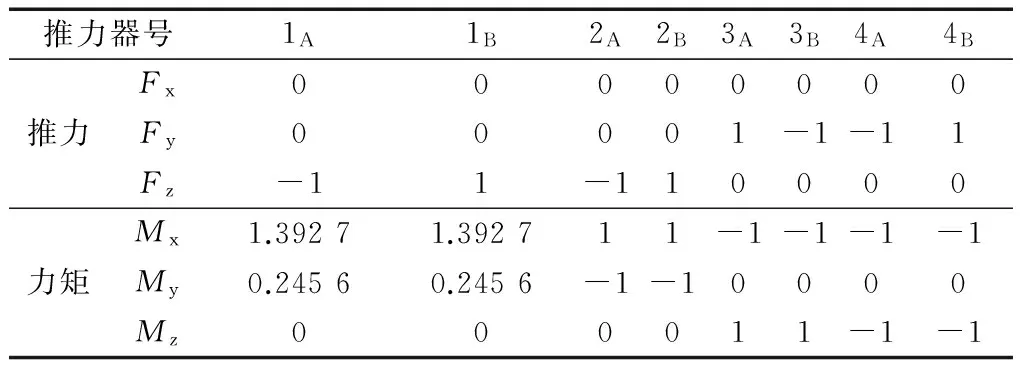
表4 推力器配置A4Tab.4 Thruster configuration table A4

根据基于最优基的最优查表法[8]，可以得到其最优推力器组合表.

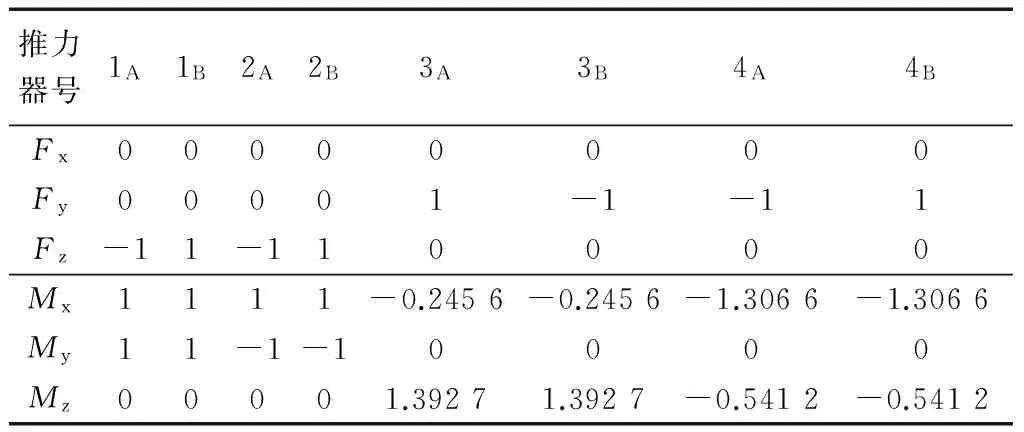
表5 推力器配置A5Tab.5 Thruster configuration table A5

表6 推力器配置A6Tab.6 Thruster configuration table A6

图1 A1力矩矢量分布Fig.1 Moment distribution of A1

图2 A2力矩矢量分布Fig.2 Moment distribution of A2

图3 A3力矩矢量分布Fig.3 Moment distribution of A3

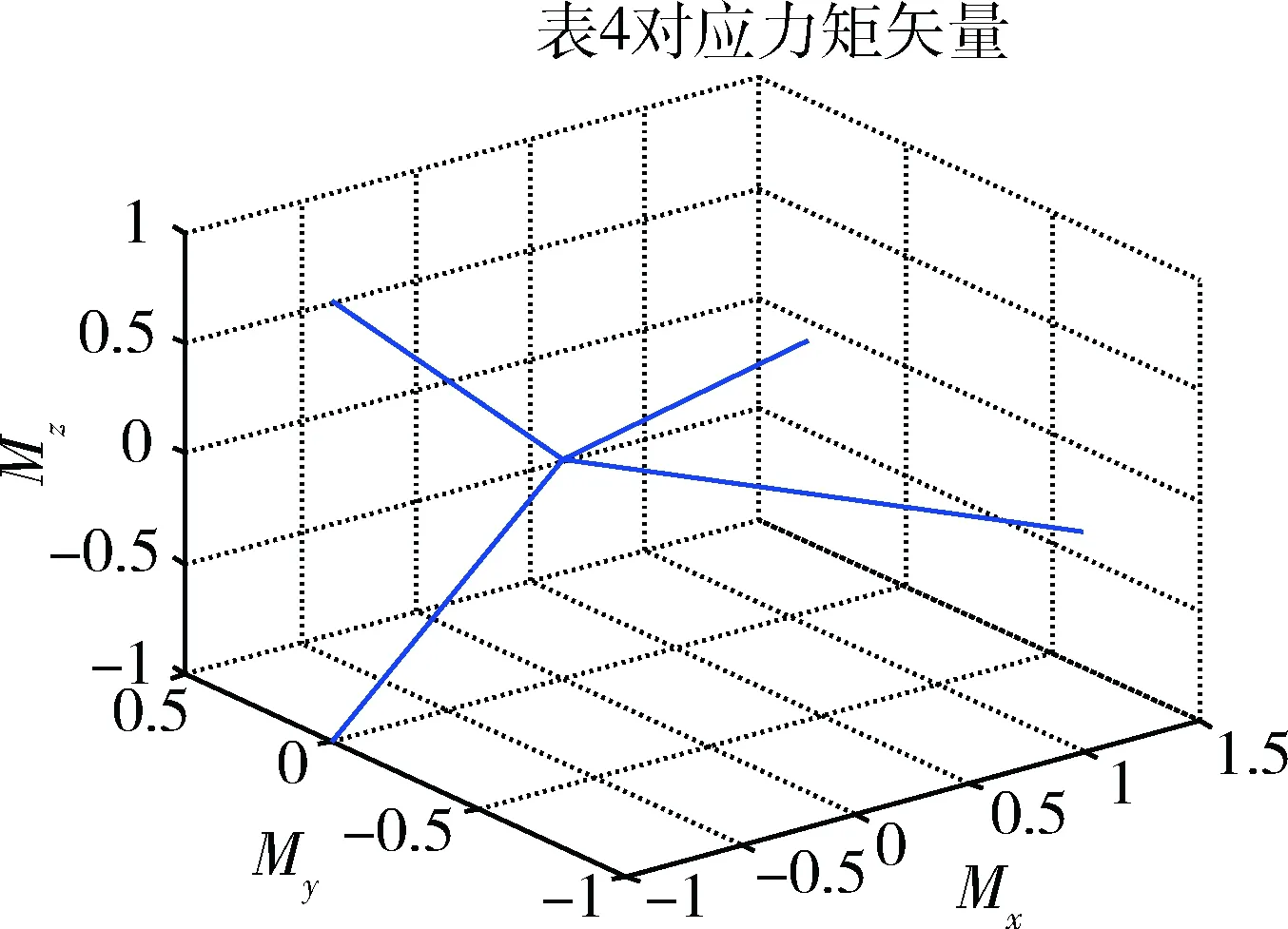
图4 A4力矩矢量分布Fig.4 Moment distribution of A4

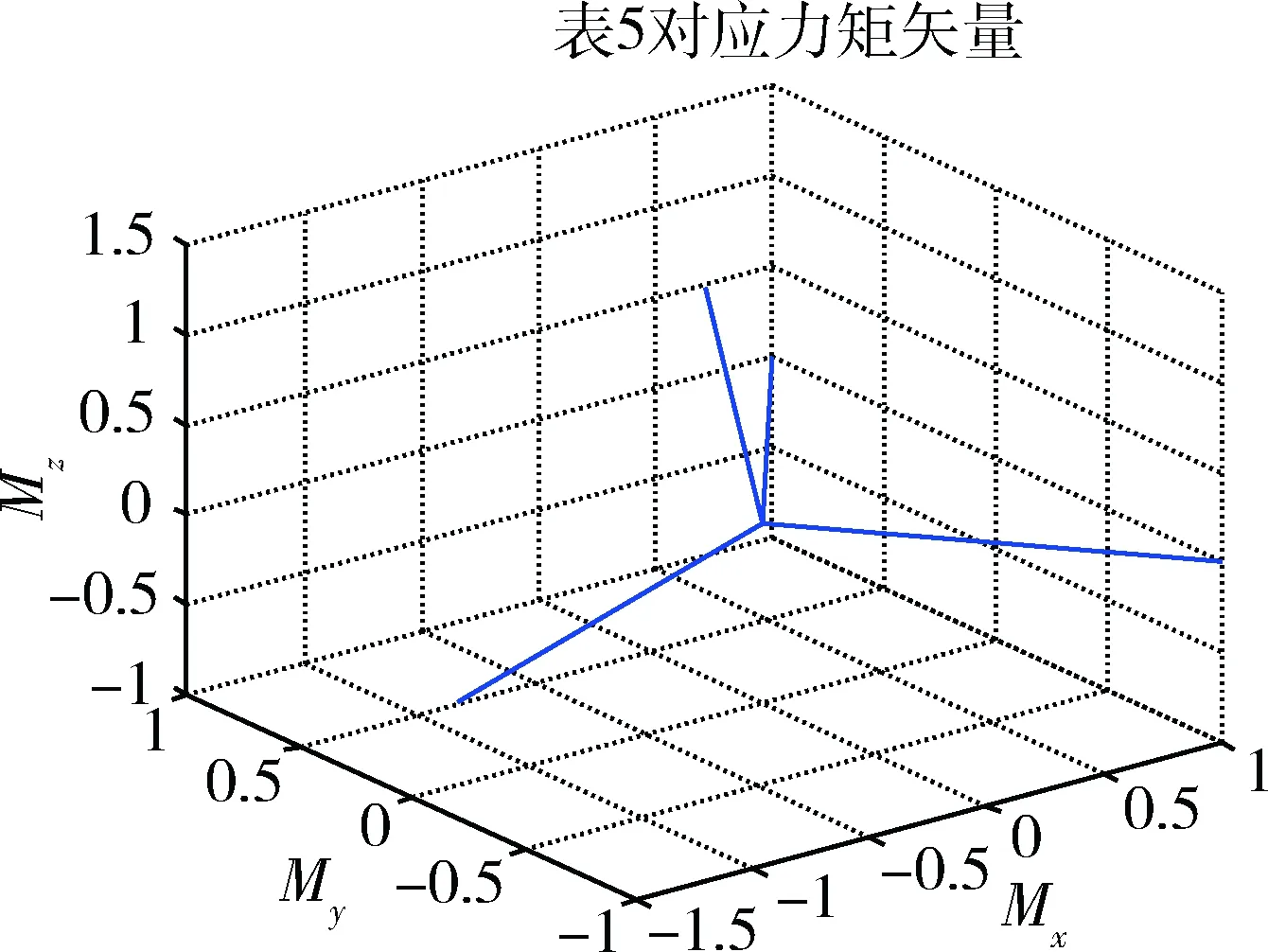
图5 A5力矩矢量分布Fig.5 Moment distribution of A5

根据上述初始条件及仿真方法，计算得到不同推力器配置在该指令区域均匀分布情况下的平均燃料消耗指标如表8所示.可以看到不同的推力器配置阵，区域平均的燃料消耗差异巨大，平均燃料消耗最大的A1燃料消耗最小A5的结果相差近27倍.

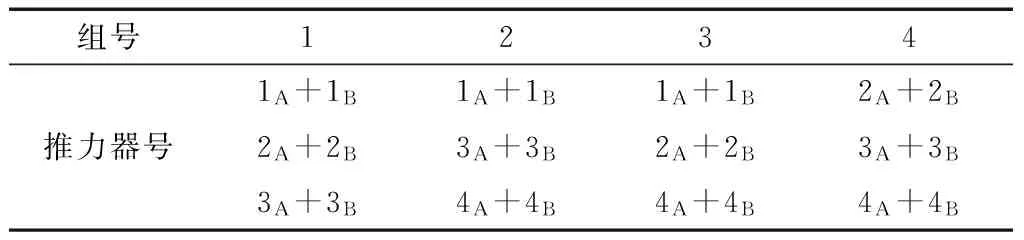
表7 最优推力器组合表Tab.7 Optimal Thruster combination table

图7 控制指令空间分布Fig.7 Distribution of command vectors

推力器配置阵A1A2A3A4A5A6平均燃耗CΩ31.21.354.094.181.164.89

3.2 优化思路

针对某一特定控制任务，通过进行细致的分析和仿真，从时间和空间上对控制指令的分布进行划分.由于我们求解的是均匀分布的平均燃料消耗，不需要精确的分布函数，只需要对任务进行方向区域的大致统计和划分，获得力和力矩六维控制指令积分变量θF,γF,θM,γM的区域范围.推力器配置阵可以根据已有的推力器安装位置、额定推力大小和约束等等信息，并根据需要的指令幅值方向和大小进行初步的设计，也可采用并参考现有推力器布局方式形成原始推力器配置阵，然后通过如下多目标规划对推力器配置阵的取值进行遍历和优化，最终选定一组具有最小平均燃料消耗的推力器配置阵.假设任务总时长为T，分段任务时间为Tl，配置优化总模型可写为如下形式：

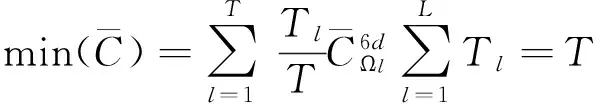
4 结 论

本文提出了区域平均燃料消耗指标，从时间和空间上对控制控制任务进行划分，把控制力和力矩矢量映射到单位球面上，针对三维和六维控制任务，分别给出了平均燃料消耗的计算方法.所提出的指标和优化思路可广泛适用于各种已有推力器配置的性能分析，对不同推力器配置的性能比较，推力器配置方案的选择以及推力器配置的进一步优化设计都具有指导意义和参考价值.

[1] ELGERSMA M, STEIN G, JACKSON M. et al. Space station attitude control using reaction control jets[C]//Proceedings of the 31stIEEE Conference on Decision and Control. New York: IEEE,1992.

[2] PETERJ W. Minimum control authority plot: a tool for designing thruster systems[J]. Journal of Guidance, Control, and Dynamics, 1994, 17(5): 998-1006.

[3] 王敏, 解永春. 航天器复杂推力器配置控制能力分析的一种新方法[J]. 中国科学技术科学, 2010, 40(8): 912-919.

WANG M, XIE Y C. Control capability analysis for complex spacecraft thruster configurations[J]. Scientia Sinica Technologica, 2010, 40(8): 912-919.

[4] RICARDO S, SANCHEZ P, ROBERTO A, et al. Robust optimal solution to the attitude/force control problem[J]. IEEE Transactions on Aerospace and Electronic Systems, 2000, 36(3): 784-791.

[5] PABLOA S, RICARDO S, SANCHEZ P. Thruster design for position/attitude control of spacecraft[J]. IEEE Transactions on Aerospace and Electronic Systems, 2002, 38(4): 1172- 1180.

[6] CRAWFORD B S. Configuration design and efficient operation of redundant multi-jet systems[C]//Proceedings of AIAA Guidance Control and Flight Mechanics Conference. Washington D.C.: AIAA, 1969: 69-845.

[7] 王敏, 解永春.航天器推力器配置的两项新性能指标[J]. 宇航学报, 2011, 32(6): 1298-1304.

WANG M, XIE Y C. New performance indices for the performance analysis of the spacecraft thruster configurations[J]. Journal of Astronautics, 2011, 32(6): 1298-1304.

[8] WANG M, XIE Y C. Design of the optimal thruster combinations table for the real time control allocation of spacecraft thrusters[C]//Proceedings of the 48thIEEE Conference on Decision and Control. New York:IEEE, 2009: 5063-5068.