半球谐振陀螺零偏温度漂移的自补偿*
2018-03-24刘吉利李建朋武志忠
刘吉利,李建朋,武志忠,李 恺
0 引 言
半球谐振陀螺是一种通过哥氏效应来获取检测对象旋转角度或角速度信息的振动式陀螺[1-2].半球谐振陀螺核心的敏感元件为半球形的谐振子,其加工材料使用的为熔融石英.熔融石英材料有着较低的热弹性阻尼,自身的品质因数很高,但作为一种温度敏感材料,其机械参数随温度的变化而变化.对半球谐振陀螺而言,一个重要的影响就是陀螺零偏随温度变化而发生漂移[3].
目前,解决半球谐振陀螺零偏温度漂移的方法主要为传统的温度建模补偿和温度控制[4].传统的温度建模补偿采用外置温度传感器的方式采集温度信息,其精度取决于陀螺温度漂移模型的准确性,但是当陀螺的温度环境(比如温度梯度、温变速率等)发生变化时,外置温度传感器采集到的温度信息不能真实的反映陀螺自身的温度情况,导致原有的温度模型不准确.因此,传统的温度建模补偿的方式误差大、实时性不高[5].另一种补偿方式是对陀螺采取温控措施,使陀螺工作在一个稳定的温度场内,这种方式无疑增加了产品的功耗、体积,而且还需设计高精度的温控方案,比较复杂[6-7].
本文提出了一种基于陀螺自身谐振频率的温度自补偿方法.该方法用半球谐振陀螺驱动模态的谐振频率来跟踪陀螺温度的变化,并对陀螺的零偏进行实时补偿.相比传统的温度建模补偿和温度控制的措施,该方法在不增加产品功耗和体积的前提下,提高了陀螺零偏温度漂移补偿的准确性和实时性.
1 半球谐振陀螺谐振频率的温度特性分析
1.1 半球谐振陀螺的谐振频率
半球谐振陀螺谐振频率可以简化为[8]:
(1)
式中,δ为半球形谐振子的圆壳厚度,D为半球形谐振子的圆壳直径(外直径),E为材料的弹性模量,ρ为材料的密度,n=2表示半球谐振陀螺工作在二阶弯曲振动模态.
当温度变化时,半球谐振陀螺谐振子的变化主要体现在两个方面:一是由于热胀冷缩引起的结构尺寸的微变形(δ、D的微变化),体现为热应力的引入[9];另一方面就是材料的机械参数,特别是弹性模量E的变化[10].下面从这两方面变化的影响来仿真、分析陀螺谐振频率的温度特性.
1.2 结构热应力变化影响的仿真分析
温度变化引起的结构热应力对陀螺谐振频率的影响,采用ANSYS软件进行仿真分析,本文建立半球谐振陀螺谐振子的三维模型,如图1所示.
该模型半球谐振陀螺谐振子的关键尺寸参数如表1所示.

图1 半球谐振陀螺的几何模型Fig.1 Geometric Model of the HRG
陀螺谐振子熔融石英的材料参数为:弹性模量为76.7 Gpa,泊松比为0.17,密度为2.2×10-6(kg/mm3),热膨胀系数为0.5×10-6/℃[11].首先对陀螺谐振子施加不同的温度载荷,仿真其在不同温度载荷点下的热应力.图2为陀螺谐振子在-40 ℃ 和80 ℃两个温度载荷点下陀螺热应力的分布情况.

表1 半球谐振陀螺模型的参数Tab.1 Mode parameters of the HRG
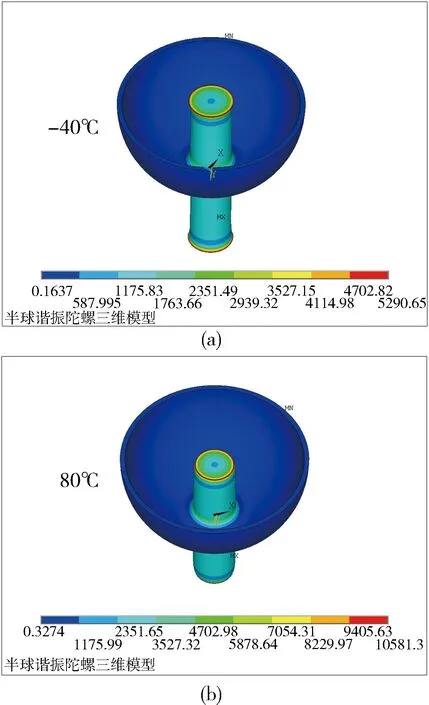
图2 半球谐振陀螺的热应力分布Fig.2 Distribution of thermal stress in the HRG
从图2可以看到,两个温度载荷点下产生的热应力沿圆壳均匀分布,且其值小于1 MPa.在叠加该热应力的基础上,对陀螺进行模态仿真分析,其工作模态的振动频率相比温度载荷施加前后几乎没有发生任何变化(仿真值均为4 517.32 Hz).由此可知,温度变化引起的结构微尺寸上的变化几乎不影响半球谐振陀螺的谐振频率.
1.3 弹性模量变化影响的理论分析
当温度变化时,陀螺材料的弹性模量会发生变化,变化量约为7.67 MPa/℃,相比其自身的数值,该变化量较小.因此,在δ,D,ρ等参数保持不变的情况下,式(1)可以展开为:

(2)

由图3可知,在-10 ℃~60 ℃温度范围内,陀螺的谐振频率变化了25 Hz,与温度正相关且具有线性关系.因此,陀螺的谐振频率完全可以用作温度传感器来使用.

图3 陀螺谐振频率与温度的关系(理论计算)Fig.3 Variations of frequency and temperature(calculated)
2 零偏温度漂移的自补偿方案
本文在已有的陀螺控制电路的基础上,增加了陀螺零偏温度漂移的自补偿模块,总体的电路架构如图4所示.

图4 自补偿方案架构Fig.4 The architecture of self-compensation scheme
补偿模块的输入包括陀螺驱动环路的谐振频率以及检测回路中VF转换的零偏输出B0.整个补偿模块在FPGA中实现,主要包含陀螺谐振频率检测以及陀螺零偏温度建模两个子模块.陀螺谐振频率检测模块将陀螺驱动回路中的频率脉冲信号转化为数字量频率信号,陀螺零偏温度建模模块通过实验的方式,得到陀螺零偏B1与数字量频率信号的关系,最后用陀螺补偿前的原始零偏输出B0减去B1,即可得到陀螺补偿后的最终零偏输出B.
2.1 陀螺谐振频率的检测
工作于力平衡模式下的半球谐振陀螺,其振形始终维持在主模态振形上.因此,补偿方案中的谐振频率采集来源于陀螺的驱动回路.半球谐振陀螺的驱动回路基于模拟控制电路,模拟解调所用的正弦波形中除了包含幅值信息外,还包含了陀螺的谐振频率信息.通过过零比较的方式,首先将该正弦信号转化为频率脉冲,再将该频率脉冲转化为补偿方案中所需的数字量频率.频率脉冲转化为数字量频率,本文采用图5所示方法.

图5 频率转换方式Fig.5 Conversion of the frequency
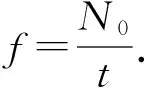
2.2 陀螺的零偏建模
半球谐振陀螺在无角速度输入的情况下,其原始零偏输出如式(3)所示[12]:
(3)
式中:K为陀螺的角增益,与陀螺的结构尺寸相关,为固定值;Δ(1/τ) 为陀螺模态间的阻尼不匹配,θτ为陀螺谐振子阻尼主轴相对于驱动轴的角度.这两个参数跟陀螺谐振子的加工误差、封装等相关,并随温度的变化而变化.对陀螺零偏的这两个参数进行测量和计算,过程比较复杂,难度较大.通常情况下,陀螺零偏温度模型的建立通过温度实验获得.
本文设置-10 ℃、5 ℃、常温、45 ℃以及60 ℃ 5个温度点,每个温度点保持至少4 h,以便真空封装下的陀螺谐振子充分预热,将每个温度点的零偏进行曲线拟合,如图6所示.
由图6可知,陀螺的零偏与温度成良好的二次多项式关系(数据与拟合曲线的相关判定系数R2为1).将陀螺零偏温度模型中温度的变化用谐振频率变化值Δf来代替,得到
B1=a×(Δf)2+b×(Δf)+c
(4)
其中,a、b、c为陀螺零偏温度模型的系数.

图6 陀螺零偏与温度的关系Fig.6 Variations of bias drift and temperature
由于每个温度点需要保持的时间较长,在保证陀螺零偏温度模型充分验证的情况下,后续实验可以适当的减少温度测量点的数目.
3 实验结果
本文在高低温温箱中开展了相关实验验证.实验设置常温、-10 ℃以及60 ℃ 3个温度点,其中常温温度点保持15 h,高低温的温度点保持至少4 h.
图7为测试得到的全温范围内陀螺的谐振频率曲线.通过图中局部放大示意图可知,本补偿方案中陀螺谐振频率检测的分辨率为0.03 Hz.
将-10 ℃、常温以及60 ℃温度点下的谐振频率值(选取每个温控点改变前一时刻的值)与温度进行一次曲线拟合,为线性关系,判定系数R2为0.99,如图8所示.
与1.3节理论仿真计算的结果相比,陀螺的谐振频率以及随温度变化的数值(-10 ℃~60 ℃温度范围内,变化了28 Hz)略有不同,这主要是因为谐振子加工尺寸偏差以及材料实际的参数不同导致的.由图8可知,实验测试得到的半球谐振陀螺的温度频率系数约为0.4 Hz /℃.因此,检测到的陀螺谐振频率所对应的温度分辨率为0.075 ℃.
选取常温下陀螺的谐振频率值为f0,与-10 ℃以及60 ℃温度点下的谐振频率值做差,最后与3个温度点下的零偏均值进行二次曲线拟合,得到如式(4)所示的二次曲线,如图9所示.
图10给出了补偿前后陀螺零偏的输出实测曲线.在-10 ℃~60 ℃温度范围内,补偿前陀螺零偏的漂移为30(°)/h,补偿后陀螺零偏的漂移为2.8(°)/h,陀螺零偏的温度稳定性提高了一个数量级.值得注意的是在实验升降温的过程中,由于温度梯度以及变温速率的影响,补偿后变温过程中陀螺零偏输出的曲线并不是很平滑,但由于波动量较小,相比最终的补偿效果可以忽略.

图7 全温范围下陀螺谐振频率的变化Fig.7 Frequency variation in full temperature range

图8 陀螺谐振频率与温度的关系(测试)Fig.8 Variations of frequency and temperature(measured)

图9 陀螺零偏漂移的温度模型Fig.9 Bias temperature drift mode of the HRG

图10 陀螺补偿前后的零偏输出Fig.10 Bias drift before and after compensation
4 结 论
本文介绍了一种基于陀螺自身谐振频率的零偏温度漂移的补偿方法,并通过实验验证了方法的可行性.采用该补偿方法,在-10 ℃~60 ℃温度范围内,陀螺零偏的温度稳定性提高了一个数量级.
[1] MATTHEWS A,Rybak F J. Comparison of hemispherical resonator gyro and optical gyros [J]. IEEE AES Magazine, 1992, 7(5): 41-46.
[2] 林凡,崔燕,陈峰浴.半球谐振陀螺的机理分析[J].中国惯性技术学报, 1996, 4(3): 44-47.
LIN F, CUI Y,CHEN F Y. Mechanism analysis of hemispherical resonator gyro[J]. Journal of Chinese Inertial Technology, 1996, 4(3): 44-47.
[3] 吕志清. 半球谐振陀螺(HRG)信号处理技术[J]. 中国惯性技术学报, 2000, 8(3): 58-61.
LYU Z Q. Signal processing technology for hemispherical resonator gyro (HRG)[J]. Journal of Chinese Inertial Technology, 2000, 8(3): 58-61.
[4] YATSENKO A,CHIKOVANI Y. Study of thermal drift modle for metallic cylindrical coriolis vibratory gyro[C]//In Proceedings of the 10thSaint Petersburg international conference on Integrated Navigation Systems.
Russia :St. Petersburg, 2003.
[5] 蔡雄,赵万良等.半球谐振陀螺组合高精度温控技术[C]//中国惯性技术学会第七届学术年会. 武汉:中国惯性技术学会,2015.
[6] 赵万良,荣义杰等.星载半球谐振陀螺惯性敏感器研究进展[C]//中国惯性技术学会第七届学术年会. 武汉:中国惯性技术学会,2015.
[7] 李广胜, 蒋英杰, 孙志强, 等.基于多项式模型的半球谐振陀螺温度漂移建模[J]. 测试技术学报, 2009, 23(6):496-500.
LI G S, JIANG Y J, SUN Z Q, et al. Temperature drift modeling of HRG based on polynomial model[J]. Journal of Test and Measurement Technology, 2009, 23(6):496-500.
[8] 张明.静电激励微机械振动环陀螺的研究[D]. 北京:中国科学院电子学研究所,2009.
ZHANG M. Electrostatically actuated micromachined vibrating ring gyroscope[D]. Beijing: The University of Chinese Academy of Sciences, 2009.
[9] 倪受东, 吴洪涛, 朱剑英, 等. 微型半球陀螺仪的误差源研究[J].传感器与微系统, 2007, 26(1): 30-32.
NI S D, WU H T, ZHU J Y, et al. Study on error source of miniature hemisphere gyrocope[J]. Transducer and Microsystem Technologies, 2007, 26(1): 30-32.
[10] 赵旭,苏中,马晓飞, 等.大温差应用环境下的MEMS陀螺零偏补偿研究[J].传感技术学报,2012,25( 8): 1079-1083.
ZHAO X, SU Z, MA X F, et al. Research on bias compensation of MEMS gyroscope under large temperature difference[J]. Chinese Journal of Sensors and Actuators, 2012,25(8): 1079-1083.
[11] SENKAL D, AHAMED M J. High temperature micro-glassblowing process demonstrated on fused quartz and ULE TSG[J]. Sensors and Actuators A , 2013,201:525- 531.
[12] CHALLONER A D, HOWARD H G, LIU J Y. Boeing disc resonator gyroscope[J]. IEEE Sensor Journal, 2014,14(10): 504-514.
