基于奇异值分解的单框架变速控制力矩陀螺角动量管理方法*
2018-03-24党庆庆徐世杰
李 焕,党庆庆,徐世杰
0 引 言
随着航天事业的发展,航天任务的多样化,各式各样的姿态控制装置应运而生.目前用于卫星姿态机动主动控制的执行机构主要包括推力器、反作用飞轮、控制力矩陀螺等.控制力矩陀螺(CMGs)由高速旋转的动量飞轮、支撑飞轮的框架和框架转动伺服系统组成.框架转动迫使动量飞轮的角动量改变方向,因而向外提供力矩输出,CMGs系统向外提供的力矩与支撑其框架伺服系统的力矩器所需输入力矩之比近似等于陀螺框架转速与航天器姿态角速度之比,故CMGs具有很高的力矩放大能力.
CMGs从框架转速是否可变可分为单框架控制力矩陀螺(SGCMGs)和变速控制力矩陀螺(VSCMGs).VSCMGs是Ford等人在1997年的AAS/AIAA的飞行力学专业会议上以“框架动量轮”的形式首次提出[1].1998年,Schaub等[2]将其命名为VSCMGs.
目前VSCMGs的操纵律设计方法在很大程度沿用了SGCMGs的设计方法,总体上讲,操纵律设计方法可分为零运动操纵律[3]、鲁棒操控律[4]、全局优化法[5]和变增益操纵律[6].
当VSCMGs仅被用作姿态控制系统的执行机构时,既可以像SGCMGs一样通过改变角动量的方向来输出大力矩,也可以像反作用飞轮(RWs)一样通过改变角动量的大小来输出力矩,前者称为CMGs模式,输出力矩大但力矩精度低;后者称为RWs模式,输出力矩小但精度高.实际上,对于常见的姿态控制任务,可以考虑的一种方案是:在大力矩输出需求时以CMGs/RWs混合模式执行,在小力矩输出时逐步锁死各CMGs框架,从而以独立的RWs模式执行.其优点是,混合模式在完成大力矩输出的同时,能够提供比SGCMGs更高的控制精度;独立的RWs模式在完成小力矩输出的同时,保证常规RWs系统的控制精度[7-9].本文围绕这一方案进行详细研究.
VSCMGs与SGCMGs相区别的显然特点是其转子转速的可变性[10-11],若操纵律设计不当,可能出现部分转子轮速低,使其力矩输出能力降低,或者部分转子轮速过高,从而易于饱和的情况,因此希望各VSCMGs的轮速能够尽量达到平衡.对VSCMGs来讲,CMGs模式与RWs模式的比例分配、轮速平衡是操纵律设计中需重点考虑的问题[12-14].这也是本文重点解决的问题.本文提出的方法将VSCMGs的CMGs模式和RWs模式分开求解同步输出,在保证VSCMGs输出精度的情况下尽量充分的利用VSCMGs的执行能力.首先,将指令力矩全部赋予CMGs模式,采用基于奇异值分解的鲁棒伪逆操纵律;并且,对于CMG接近奇异时奇异方向存在的力矩偏差采用RWs模式进行补偿;然后,设计全局收敛的转速跟踪率,且参考转速随着VSCMGs角动量的变化而变化.最后,在操纵律中加入死区补偿使所有框架角转速远离死区.
1 系统动力学建模
本文用到以下3个坐标系:惯性坐标系fi(oxiyizi),轨道坐标系fo(oxoyozo)和航天器本体坐标系fb(obxbybzb).其中,轨道坐标系原点固联在航天器质心o,ozo轴沿当地垂线指向地心;oxo轴在轨道平面内垂直于ozo轴,指向航天器运动方向;oyo轴按右手定则与oxo,ozo组成正交系,考虑到惯性系的等价性,假设在初始时刻惯性系和轨道系重合.航天器本体坐标系与航天器固联,原点ob位于航天器质心.obxb,obyb,obzb三轴固定在航天器本体上,构成右手坐标系.当航天器本体相对于轨道坐标系的3个姿态角为零时,各轴指向与轨道坐标系对应各轴指向相一致.
1.1 姿态运动学与动力学方程
对于三轴稳定航天器的对地定向运动,采用3-1-2转序,参考坐标系选为轨道坐标系oxoyozo.轨道系到本体系的姿态转换矩阵为Azxy(ψ,φ,θ),φ,θ,ψ分别为滚动角、俯仰角和偏航角.航天器本体系相对于惯性坐标系的绝对角速度矢量ωb=[ωbxωbyωbz]T在本体坐标系中的分量为
ωb=ωbo+Azxy(ψ,φ,θ)ωo
(1)
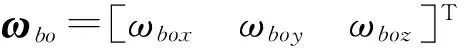
单刚体航天器姿态动力学方程描述为
(2)
式中:Ib为单刚体航天器相对于其质心ob且在本体坐标系中的转动惯量矩阵;Te为作用在航天器上的外力矩.
1.2 VSCMGs系统的动力学方程
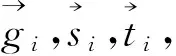

图1 VSCMGs示意图Fig.1 Schematic diagram of VSCMGs
记转子相对惯性系的角速度为ωwi,在框架坐标系fci(ocigisiti)中,ωwi可表示为
(3)
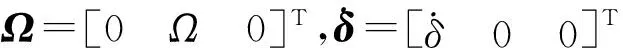
转子i相对惯性系的角动量在fci中表示
(4)
记框架相对惯性系的角速度为ωgi,在fci中
(5)
因此fci中框架相对陀螺质心的绝对角动量为
(6)
其中,Igi=diag{Iggi,Igsi,Igti}为第i个VSCMG的框架相对陀螺质心的惯量矩阵.
VSCMG角动量为转子和框架角动量之和
(7)
其中,Iwi=diag{Iwgi,Iwsi,Iwti}为第i个转子相对于惯性系的惯量矩阵,ωwi为转子相对惯性系的角速度;Igi={Iggi,Igsi,Igti}为第i个VSCMG的框架相对陀螺质心的惯量矩阵,ωgi为框架相对惯性系的角速度.将其转换到航天器本体坐标系中为
(8)
陀螺群的总角动量为[17]
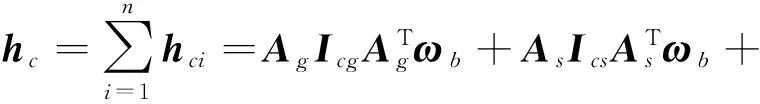
(9)

(10)
其中,算子d[x]定义为d[x]=diag{x1,x2,…,xn}.
根据动量矩定理可得系统动力学方程为
(11)

(12)
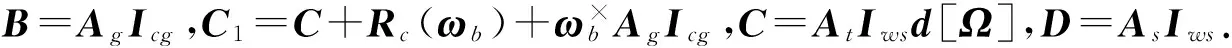
(13)
式中,C=AtIwsd[Ω],D=AsIws分别为框架转动和动量轮转子速度变换引起角动量大小变化产生的力矩矩阵,At和As为二者的力矩系数矩阵.
2 VSCMGs操纵率设计
VSCMGs操纵律(角动量管理)设计是陀螺群动力学的逆问题,即根据陀螺群框架转角的现况,合理分配各框架转速指令和动量轮转子转速指令,使陀螺群的输出力矩与航天器姿态控制系统要求的指令控制力矩相等.VSCMGs角动量管理问题将CMG模式和RW模式分开分步求解.由于操纵律是线性的,因此满足齐次性和叠加性,最后将所有求得的指令框架角速度和转子角加速度相加即可.
2.1 力矩输出部分操纵律
本节需要解决的问题有两个:一个是CMGs模式的操纵律设计;另一个是CMGs模式下的误差计算及其RWs补偿设计.为解决伪逆加零运动操纵律无法使VSCMGs脱离显奇异点的问题,给出基于奇异值分解的鲁棒伪逆操纵律的具体设计过程.
2.1.1 CMGs模式的操纵律设计
若指令力矩全部赋予CMGs模式,则有
(14)
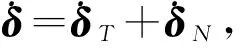
(15)

(16)

(17)
为了避免陀螺构型陷入奇异时,伪逆解不存在,可引入最小力矩误差的鲁棒伪逆操纵律
(18)

(9)
可见,力矩误差的引入只使得当系统接近奇异时,第3个奇异值由0变为ξ,而其它两个奇异值并没有改变,力矩误差只有在CMGs接近奇异时奇异值最小的方向产生.因此可使得采用此操纵律时,能在避免显隐奇异的同时使力矩误差最小,有效保证了力矩的输出精度,也保证了下面求解RWs模式下的转子角加速度解的存在性.至此,我们完成了CMGs模式下的操纵律设计.
2.1.2 RWs模式的操纵律设计
RWs模式的操纵律设计可以参考单独采用飞轮作为系统执行机构的航天器姿态控制问题.此时的指令力矩为Terror.不同于单一的飞轮,VSCMGs中的飞轮构型时变化的,此时飞轮的构型矩阵为As,他随着框架角的变化而变化,因此存在奇异问题.
飞轮操纵律将指令控制力矩分配给飞轮组中的每个飞轮,故要解算每个飞轮的指令角加速度,从而使得当驱动各个飞轮按指令运转时,飞轮组输出的合成力矩等于期望的控制力矩.
飞轮组输出的控制力矩可写为一般式
(20)

由广义逆定理求得能耗最小的控制律
(21)
由于转子个数大于控制所需自由度,故RW控制律也存在零运动.
至此完成RW模式下的操纵律设计.
2.2 零运动操纵律设计
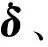
2.2.1 VSCMGs框架避奇异
VSCMGs考虑框架避奇异问题时暂不需要考虑转子转速的变化.通过零运动进行框架避奇异的基本思路是根据所定义的奇异度量,期望通过零运动的框架再构型使其值有所增大.为了保证所设计的角动量管理算法简洁明了,定义式(17)中的第3个奇异值为CMGs构型的奇异度量
κq=σ3
(22)
本文利用优化理论中的梯度法来进行零运动设计.构型奇异度量的梯度为
(23)

(24)
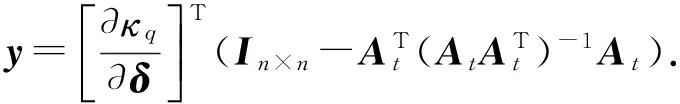
(25)
将式(25)代入式(24),得到具体的空转指令
(26)
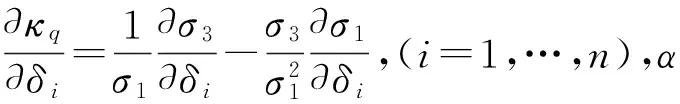
(27)
所得结果代入式(26),得相应奇异度量下的零运动操纵律.
2.2.2 VSCMGs转子转速平衡
为了充分的利用VSCMGs构型的冗余和转子的变速性能,同时防止转子转速过高或者过低,需要设计相应的转子转速跟踪率,使转子转速能够在一个比较合理的范围内Ω∈(Ωmin,Ωmax)变化.
(28)
其中,h为VSCMGs的角动量,h0max为转子最大转速时的标称角动量.λi(i=1,2,3,4)为常数,取值范围分别为λ1∈(0.8,0.95),λ2∈(1.05,1.2),λ3是常值,与VSCMGs的构型有关,金字塔构型时取2.56.
转子角加速度为
(29)
利用Lyapunov直接法分析状态量偏差在零运动下的运动规律.不难发现,该跟踪率是全局渐进稳定的.但跟踪率只有在CMGs非奇异的状态才能使用.下面对转子转速跟踪产生的力矩进行补偿.
转子转速跟踪产生的力矩
(30)
这一部分力矩采用CMG模式进行抵消,很容易计算此时所需的框架角速度
(31)
整体的框架角零运动为
(32)
2.3 CMGs忽略项补偿
以上设计操纵律时,对VSCMGs的动力学方程中的框架角加速度、本体角速度等项进行了简化处理,只保留了关于框架角速度的线性项.为了进一步提高VSCMGs的力矩输出精度,在已经求解出框架角速度的情况下,可计算出这些忽略项产生的力矩,通过RWs模式进行补偿.CMGs模式的计算误差为
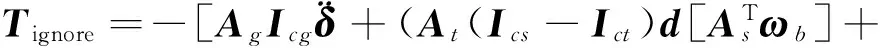
(33)
采用RW模式进行补偿
(34)
最终设计完成的转子角加速度为
(35)
相应的框架角速度为
(36)
3 仿真验证
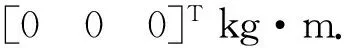

图2 金字塔构型Fig.2 Pyramid configuration

参数数值标称角动量/(N·m·s)25转子转速/(r/min)3600·7200转子标称转速/(r/min)6000最大输出力矩/(N·m)25最大框架速率/((°)/s)60最小框架速率/((°)/s)0.05
本文仿真两个算例,分别为操纵律存在死区和忽略项补偿及操纵律没有死区和忽略项补偿.仿真中的所有初始姿态角均设置为[0.4 0.5 -0.3]T,对于VSCMG模型中的电机参数只考虑死区的影响.
3.1 case 1没有误差项及死区补偿
本算例没有框架角速度和操纵律求解时的忽略项补偿,此时框架角速度和转子角加速度的求解为
(37)
仿真结果如图3~10 所示,显然在该情况下,转子转速具有较好的跟踪效果(图4),大概在50 s以后转子角速度趋于一致.并且即使是在三轴姿态同时机动的情况下(图3),转子角加速度(图5)与框架角速度(图6)都控制在合理范围内.
由于CMGs模式始终远离奇异(图7),因此力矩输出部分是由CMGs模式完成的,而RWs模式产生的力矩(图9)主要是用于转子转速跟踪.但由于缺少对死区和忽略项进行补偿,因此力矩输出误差略大(图8).
3.2 case 2有误差项及死区补偿
该算例的力矩输出采用仿真结果如图11~图18 所示.显然该情况下相比于case 1,最大的变化在于力矩输出误差(图16)相比于图8有了很大数量级的降低, 由于引入了对死区和忽略项的补偿.
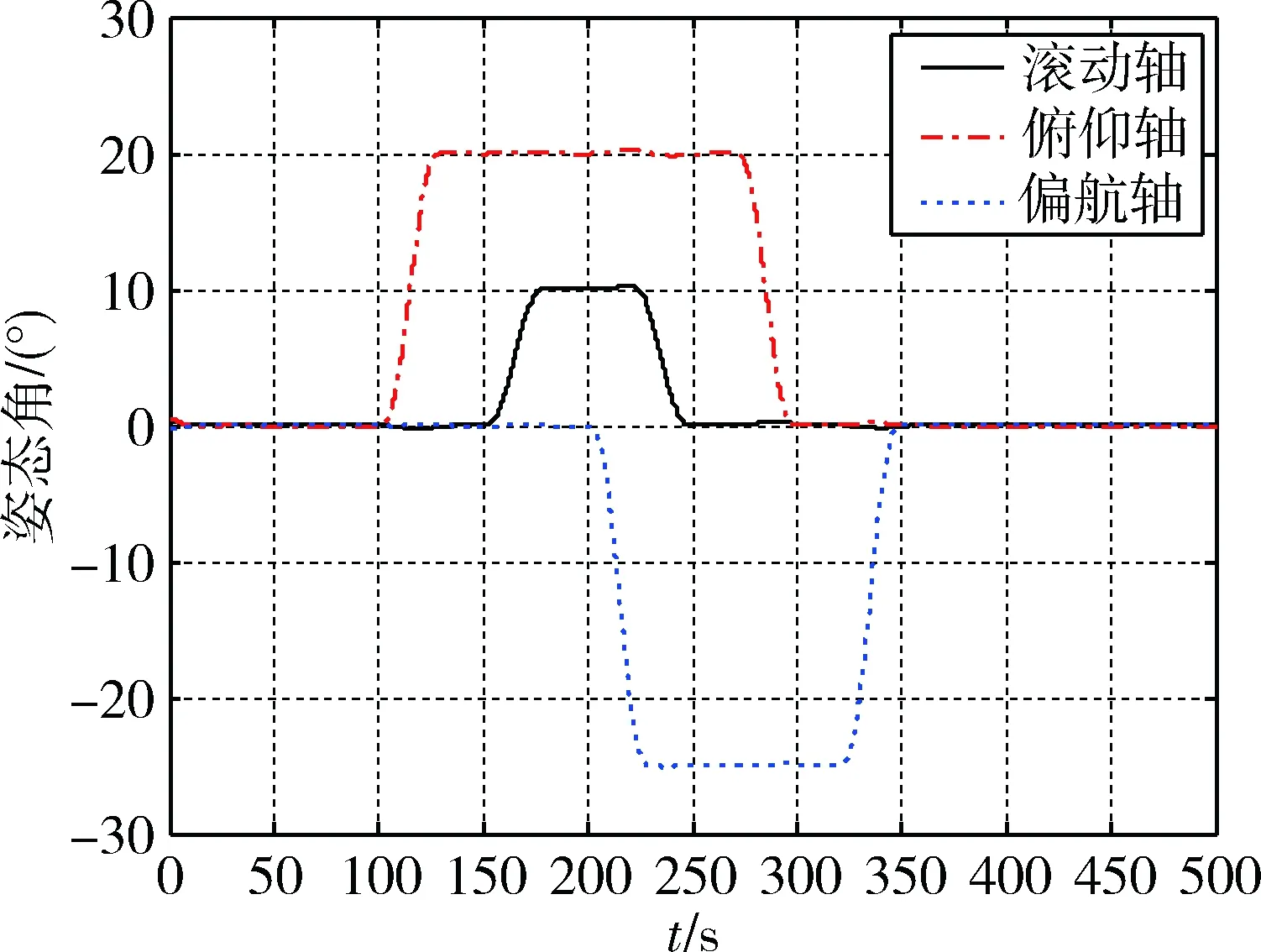
图3 case 1的姿态角Fig.3 Attitude angle in case 1

图4 case 1的VSCMGs的转子角速度Fig.4 Rotor angular velocity of VSCMGs in case 1

图5 case 1的VSCMGs的转子角加速度Fig.5 Rotor angular acceleration of VSCMGs in case 1

图6 case 1的VSCMGs的框架角速度Fig.6 Frame angular velocity of VSCMGs in case 1
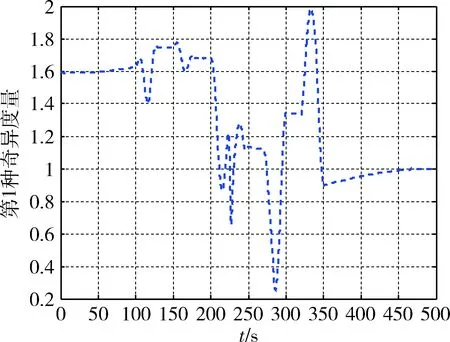
图7 case 1的CMGs奇异度量Fig.7 Singular metric of CMGs in case 1
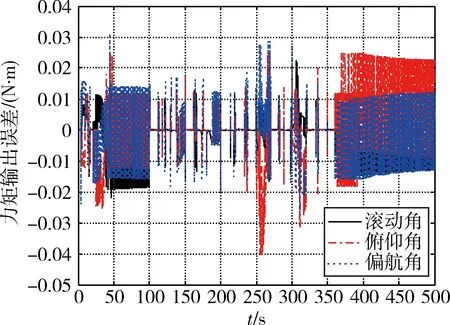
图8 case 1的力矩输出误差Fig.8 Moment output error in case 1

图9 case 1的RWs输出力矩Fig.9 Output torque of RW in case 1
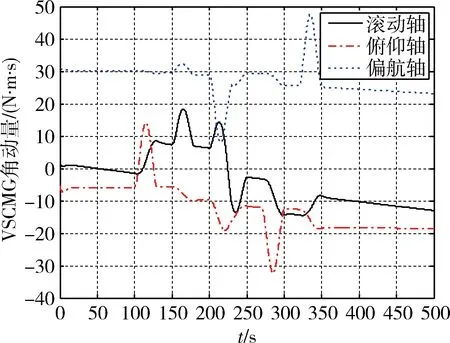
图10 case 1的VSCMGs角动量Fig.10 Angular momentum of VSCMG in case 1
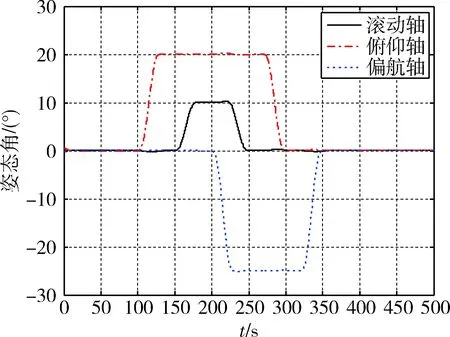
图11 case 2的姿态角Fig.11 Attitude angle in case 2
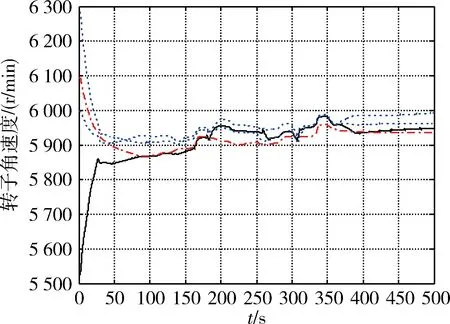
图12 case 2的VSCMGs的转子角速度Fig.12 Rotor angular velocity of VSCMGs in case 2
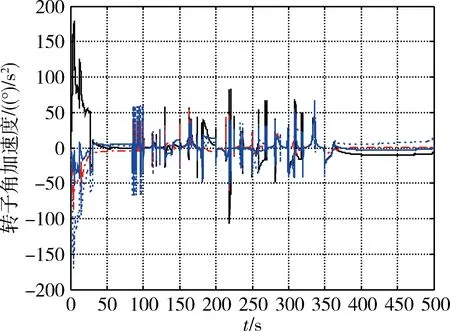
图13 case 2的VSCMGs的转子角加速度Fig.13 Rotor angular acceleration of VSCMGs in case 2

图14 case 2的VSCMGs的框架角速度Fig.14 Frame angular velocity of VSCMGs in case 2

图15 case 2中CMGs奇异度量Fig.15 Singular metric of CMGs in case 2

图16 case 2的力矩输出误差Fig.16 Moment output error in case 2

图17 case 2的RWs输出力矩Fig.17 Output torque of RW in case 2
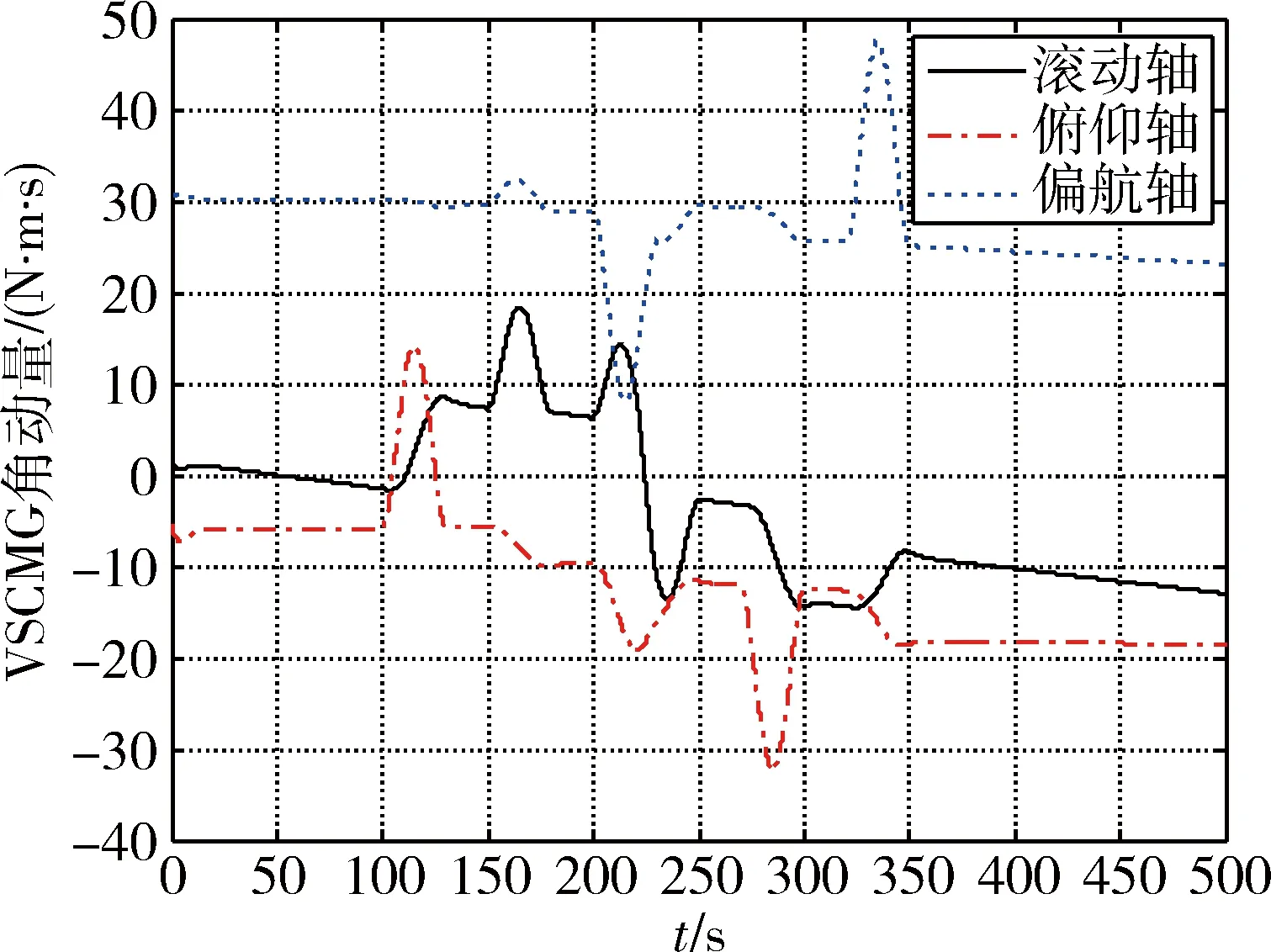
图18 case 2的VSCMGs角动量Fig.18 Angular momentum of VSCMG in case 2
但由于死区补偿和忽略项补偿均是在最后一步进行的,而转子转速跟踪率在设计时并没有考虑死区和忽略项补偿,因此对于转子角速度的收敛性有一定的影响,但总体来说,转子角速度依旧能够保持较好的一致性(图12),并且可以随着角动量的变化相应的转子角速度也发生相应的变化.由于本文考虑的是理想电机模型,因此不考虑控制中电压波动.因此,操纵律达到了期望的要求.
4 结 论
本文以VSCMGs为研究对象,对其进行姿态动力学建模和详尽的操纵律设计.通过将CMGs模式RWs模式分开分步求解,在保证VSCMGs输出精度的情况下尽量充分的利用VSCMGs的执行能力.重点解决基于奇异度量的混合模式指令力矩输出,零运动作转子轮速平衡,零运动作框架构型避奇异,框架角速度死区非线性处理以及忽略项的补偿等问题,并给出相应的理论分析.最后,以理论分析为基础,重点对VSCMGs在CMGs/RWs混合模式下的操纵律进行仿真验证.根据仿真结果可知,基于这些操纵律,VSCMGs可实现大角度快速姿态机动操作.
[1] FORD K A, CHRISTOPHER D H. Flexible spacecraft reorientations using gimbaled momentum wheels[C]//Proceedings of the AAS/AIAA Astrodynamics Conference.San Diego, AAS 97-723,1997.
[2] SCHAUB H, VADALI S R, JUNKINS J L. Feedback control law for variable speed control moment gyros[J]. The Journal of The Astronautical Sciences, 1998,46(3):307-328.
[3] JOHN E F. A Reactive torque control law for gyroscopically controlled space vehicles[R].NASA TM X-64790,N74 10419,1973.
[4] CRENSHAW J W.2-Speed, a single gimbal cmg attitude control system[C]//AIAA Guidance and Control Conference.New York,1973.
[5] YOSHIKAWA T. Steering law for roof type configuration control moment gyro system[J]. Automatica, 1977,13:359-368.
[6] RICHARD V, RIPER V, SAM P L. A new fail operational control moment gyro configuration[R]. AIAA1971-936.
[7] NAKAMURA Y, HANAFUSA H. Inverse kinematic solutions withsingularity robustness for robot manipulator control[J]. Journal of Dynamic Systems, Measurement, and Control, 1986, 108(3): 163-171.
[8] PARADISO J A. global steering of single gimbaled cmgs using a directed search[J].Journal of Guidance, Control, and Dynamics, 1992, 15(5): 1236-1244.
[9] VADALI S R, OH H S, walkEr S R. preferred gimbal angles for single gimbal control moment gyros[J]. Journal of Guidance, Control, and Dynamics, 1990, 13(6): 1090-1095.
[10] TOKAR E N. Efficient design of powered gyrostabilizer systems[R]. Cosmic Research, 1978,16-23.
[11] YOON H, TSIOTRAS P. spacecraft adaptive attitude control and power tracking with variable speed control moment gyroscopes[J]. Journal of Guidance, Control, and Dynamics, 2002, 25( 6): 1081-1090.
[12] 贾英宏. 航天器姿态与能量一体化控制研究[D]. 哈尔滨: 哈尔滨工业大学, 2004.
[13] 贾英宏, 徐世杰. 采用平行构型变速控制力矩陀螺群的航天器姿态控制[J].宇航学报, 2003, 24(5):490-495.
JIA Y H,XU S J.Spacecraft attitude control using parallel-gimbaled variable speed control moment gyros group[J].Journal of Astronautics,2003, 24(5):490-495.
[14] 张景瑞, 李俊峰. 航天器能量/姿态一体化控制器设计与及功率规划[J]. 清华大学学报, 2005, 45(2): 280-284.
ZHANG J R,LI J F.Integrated power and attitude control system (IPACS) and power controller for spacecraft[J].Journal of Tsinghua University(Science and Technology) , 2005, 45(2): 280-284.
[15] 孙志远, 金光, 张刘,等. 基于自适应高斯伪谱法的SGCMG无奇异框架角轨迹规划[J]. 宇航学报, 2012, 33(5):597-604.
SUN Z Y,JIN G, ZHANG L,et al.SGCMG non-singularity trajectory programming algorithm based on adaptive Gauss pseudospectral method[J].Journal of Astronautics,2012, 33(5):597-604.
[16] 刘军, 韩潮. 应用变速控制力矩陀螺的卫星姿态机动的非线性控制[J]. 航天控制, 2007, 25(5):33-38.
LIU J, HAN C.Nonlinear control of attitude maneuver for satellite using variable speed control moment gyros[J].Aerospace Control,2007, 25(5):33-38.
[17] HUANG X, JIA Y, Xu S, et al. A new steering approach for VSCMGs with high precision[J]. Chinese Journal of Aeronautics , 2016, 29(6):1673-1684.
