姿态异常下的星体自旋角速度确定方法*

雷拥军，李明群

0 引 言

三轴稳定卫星控制系统在轨异常时往往会触发喷气控制导致星体高速翻滚[1]，根据自旋刚体内能耗散下方向稳定性的最大轴原理[2]，星体在轨最终绕最大惯量轴旋转.在星体大旋转角速度运动下绝大部分敏感器将无法工作，甚至角速度幅值超过测量部件陀螺量程而无法获取反映实际星体角速度的测量信息，导致地面难以了解星体实际运行状态.

一旦卫星在轨姿态异常发生星体高速旋转，根据太阳翼法线、自旋轴和太阳矢量关系确定整星能源供给状态，并根据执行机构安装与自旋轴方位关系制定有效消旋及进动控制策略并选取合适执行机构，以及对消旋与进动控制实施效果及时评估等[3]，均是保证卫星系统安全性的重要手段.因而如何在姿态敏感器测量信息严重匮乏情况下准确获取自旋角速度成为在轨卫星姿态异常下的急需.

与单自旋卫星结构设计遵循把卫星最大主惯量轴转动惯量设计为远大于其它两轴的基本原则[4-5]不同，基于零角动量三轴稳定控制卫星由于星体三轴均可独立施加主动控制，从控制角度来说一般对星体三轴转动惯量设计没有特别约束要求，当最大轴与中间轴的转动惯量之差不大再加上不可避免的结构设计参数偏差时，根据设计质量特性参数计算得到的最大惯量轴将与实际存在很大偏差，从而无法作为卫星姿态异常后的紧急处置措施的依据.

为实现三轴稳定卫星在轨长期运行高可靠性及安全性，除了正常运行时作为姿态测量备份外，太阳敏感器通过测量太阳相对方位，并与星体角速度测量结合为系统姿态基准丢失后星体特定方位对日实现提供信息，因此具有体积功耗小且可靠性高的太阳敏感器在卫星上广泛使用[6-7]，太阳敏感器可作为星体姿态异常后自旋角速度确定的重要信息源.

针对三轴稳定控制卫星在轨姿态异常高速自旋情况，本文提出了一种基于太阳敏感器测量的星体自旋角速度确定方法，结合敏感器测量误差及测量原理对自旋角速率测量精度进行了分析，给出在不改变太阳敏感器遥测数据方式下保证不同自旋角速率的确定精度的策略，可为失控卫星在轨挽救所采取的消旋与进动控制实施策略制定提供依据及其效果评估途径.

1 星体自旋角速度确定原理

太阳敏感器组件一般采用由两个互相垂直安装的狭缝敏感器测量太阳矢量在敏感器坐标系下的方位.记太阳敏感器组件的测量坐标系为oxsyszs，其中敏感器的瞄准轴为zs，在与轴zs垂直的平面xsoys上，两条狭缝分别与xs和ys轴平行.

太阳敏感器的测量为太阳矢量在基准面平面或平面上的投影与瞄准轴之间夹角的正切，分别记为mx与my.根据太阳敏感器测量输出，可得太阳单位矢量在敏感器坐标系下的方位为

(1)

并由敏感器安装矩阵MSB，可得矢量在星体坐标系下的测量为

(2)

在短时间内，忽略太阳矢量在惯性空间变化，因此在不同时刻测量到的BS变化可均认为由卫星本体的转动引起.若太阳敏感器在t1、t2和t33个连续不同时刻测量输出得到的太阳矢量在星体下向量分别为S1、S2与S3，并由此可得两变化向量:

S21=S2-S1，S32=S3-S2.

记卫星自旋轴在星体系下的单位向量为e及星体绕自旋轴旋角速率为ω，则星体自旋角速度可表示为ω=ωe.在时刻t姿态矩阵为A(t)，在时刻t+Δt姿态矩阵为A(t+Δt)，则有

A(t+Δt)=ΔA(Δt)A(t)

(3)

其中

ΔA(Δt)=cosφI+(1-cosφ)eeT-sinφe×

其中，φ=ωΔt，

假设在[t1,t3]时间段内测量星体自旋轴e及自旋角速率为ω维持不变，则对于向量S1、S2与S3满足如下关系:

S2=ΔA(t2-t1)S1，S3=ΔA(t3-t2)S2

(4)

其中ΔA(t2-t1)、ΔA(t3-t2)与式(3)中ΔA(Δt)形式相同，且其中θ1=ω(t2-t1)与θ2=ω(t3-t2).

由式(4)有

eTS21=eT(ΔA(t2-t1)S1-S1)

=eT[(1-cosφ1)(eeT-I)-sinφ1e×]S1=0

同理有eTS32=0，故S21、S32均与自旋轴e垂直，其几何关系如图1所示，其中θ为两变量向量S21、S32之间的夹角，o′为向量S21、S32所在平面与自旋轴e的交点.

当自旋轴e与BS1不平行时可求得

(5)

根据自旋轴e与太阳矢量不同时刻在星体下表示BS1、BS2与BS3的夹角均相等可知，由向量S21、S32所在平面三角可求得

即得自旋角速率ω为

(6)

若能保证太阳敏感器连续测量间隔Δt均恒定时θ=θ1=θ2，则自旋角速率为

(7)

当由敏感器测量获取太阳矢量在星体系下时间序列{BSk,k=1,2,…}，根据式(5)与式(6)即可求解出卫星在星体下的自旋角速度.

2 自旋角速率确定误差与精度改进策略

考虑敏感器的测量误差时，不妨令mx与my对应测量误差分别为Δmx与Δmy，其为互不相关的零均值高斯白噪声，对应的方差分别为

σ2[Δmx]=σ2[Δmy]=r2(r>0)

考虑实际过程中rs为小量，式(1)所示太阳敏感器测量方程可写为

(8)

(9)

假设太阳敏感器连续测量间隔Δt恒定，根据图1 所示关系有θ=θ1=θ2且

(10)

其中θse为太阳矢量与自旋轴e之间夹角.

记自旋角速率测量误差为Δω，当敏感器测量及Δω·Δt为小量时,由式(7)及式(10)有

(11)

其中ΔS21与ΔS32分别为敏感器测量导致的向量S21与S32偏差，其为

ΔS21=ΔS2-ΔS1，ΔS32=ΔS3-ΔS2

ΔSi为ti(i=1,2,3)时刻敏感器测量的太阳矢量偏差，对于任意不同时刻ΔSi可认为是不相关的.

不失一般性，后续分析不妨均假设太阳敏感器坐标系与星体坐标系一致，即安装矩阵MSB为单位阵，为了简洁故略去表示向量所在坐标系的左上标符号.若实际两坐标系不重合时，以太阳敏感器坐标系重新定义星体坐标系，在重定义星体坐标系下完成相关运算后再转换回原来星体坐标系即可.

(12)

由如下关系式:

可将式(12)右端三项分别表示为

其中S21z、S32z分别表示S21、S32的第3个分量，于是式(12)可写为

当θ为小量时，有S21z≈S32z，则

由图1可知，S21在自旋轴e垂直的平面内随星体转动绕e作周期运动，且有

(13)

利用不等式(13)，E(v2)可表示为

(14)

当θ=ωΔt为小量时，式(14)可近似表示为

(15)

由式(15)易知，采用太阳敏感器测量星体自旋角速率精度除与敏感器精度直接相关外，还具有如下性质：

1)当太阳矢量与自旋轴e之间夹角θse越小时则自旋角速率测量误差Δω越大，特别是两矢量重合时则无法测量出星体自旋角速率.

2)角速率测量误差Δω为零均值且方差呈现周期变化特性，当自旋轴e与敏感器瞄准轴zs重合时方差呈现为常值特性.

3)自旋角速率确定精度E(Δω2)与实际自旋角速率ω的平方成反比关系，与太阳矢量测量的间隔时间Δt的3次方成反比关系.

如在星体消旋措施实施过程中，当星体自旋角速率越来越小时，根据上述特性3)可知由于连续两次间隔数据进行自旋角速率确定时误差将变得越来越大.对于特定的自旋角速率ω，由其确定精度与太阳矢量测量间隔时间3次方成反比关系，在维持星上遥测数据不变情况下，通过加大确定自旋姿态数据间隔是提高确定精度的有效方式.

图2给出了利用多采样间隔的太阳测量矢量进行做差处理得到自旋角速度求解的太阳矢量变化量，其中Sn、Sn+1、…、Sm、Sm+1、…、Sn+k、Sn+k+1、…为等间隔太阳矢量测量在星体下的表示，k≥1，m>n.

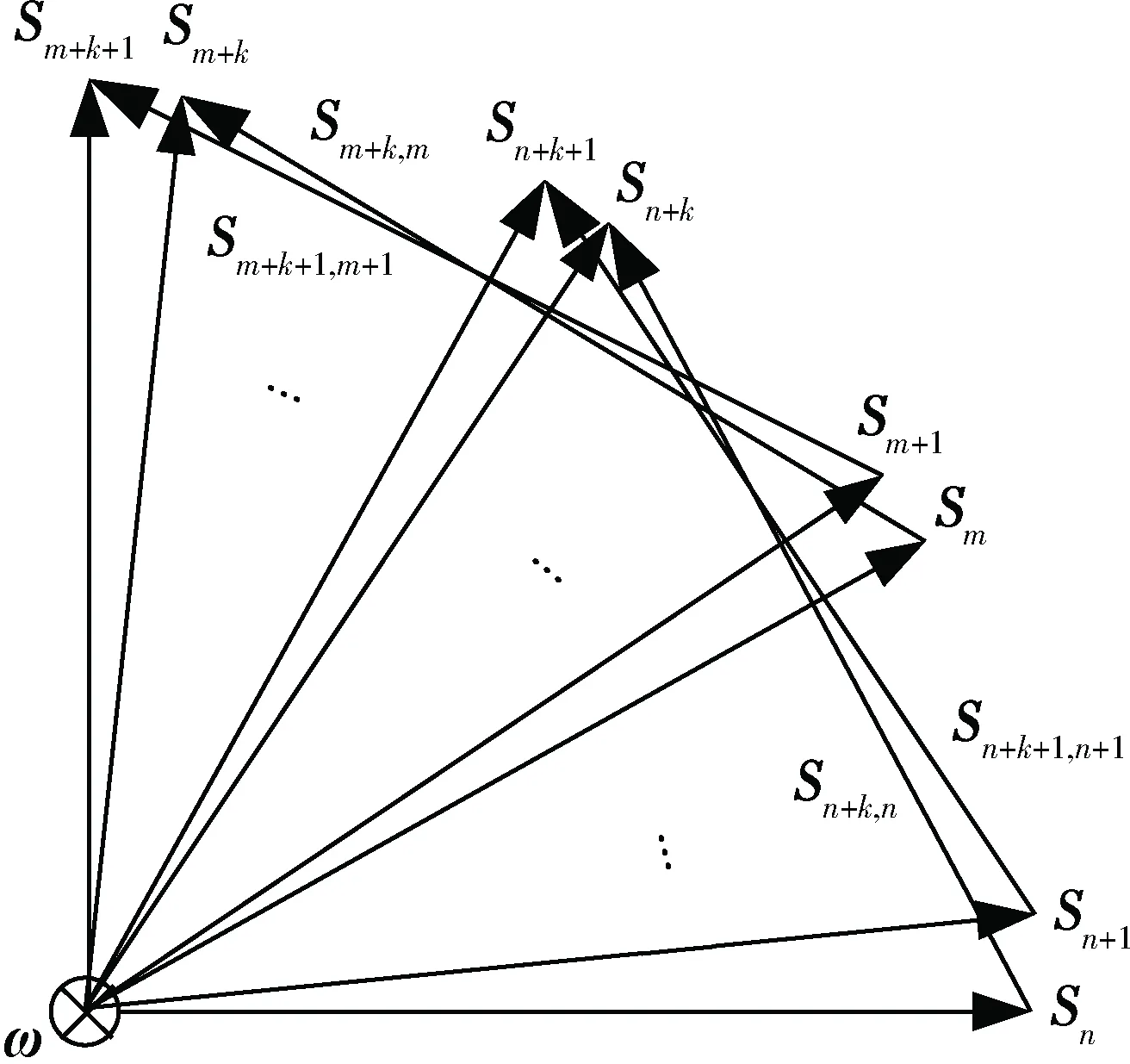
图2 考虑测量精度影响的太阳矢量变化量选择示意图Fig.2 Diagrammatic sketch of selected solar vector variations for spinning angle rate determination in case of measurement errors

依据第1节中给出的自旋轴自旋角速度测量原理，可得利用不同测量间隔数据下的自旋轴单位矢量及角速率计算公式为

(16)

(17)

其中Sm+k,m=Sm+k-Sm，Sn+k,n=Sn+k-Sn.当取m-n=1与k=1时，式(16)、(17)分别与式(5)、(7)相同.

3 仿真验证及应用情况

3.1 数学仿真验证

设定太阳敏感器测量精度为0.01°(3σ)，其光轴指向沿星体-Y轴，以采样间隔Ts=0.5 s获取测量原始数据.卫星自旋轴在星体下的坐标为[0.183 0.913 0.365]T，与太阳矢量夹角为24.1°，如图3所示.

图3 星体自旋轴与太阳矢量夹角Fig.3 Angle between spinning axis and solar vector

当星体角速度幅值为36(°)/s时，选取式(16)与式(17)中的m=2、n=1与k=1进行自旋角速度确定，将Δt=0.5 s、θse=24.1°、r=0.01°及θ=18°代入式(14)中第2个不等式右端，计算得到理论确定误差为0.717(°)/s(3σ).数学仿真验证确定的自旋轴方位及自旋角速率分别如图4～5所示，并由图5可知自旋角速度确定精度约为0.7(°)/s(3σ)，与理论结果相吻合.

当星体角速度幅值消旋降至3(°)/s时，选取式(16)～(17)的m=2、n=1与k=4，对应自旋角速度确定所使用太阳敏感器测量数据时间间隔为原始采样间隔的4倍，同前由Δt=4Ts=2 s、θse=24.1°、r=0.01°及θ=6°可计算得理论确定误差为1.583(°)/s(3σ).数学仿真验证确定的自旋角速率如图6所示，由此可知其确定误差为1.58(°)/s(3σ)，与理论结果相吻合.

图4 自旋轴在星体系的分量Fig.4 Spinning axis in satellite body-fixed reference frame

3.2 应用情况

将所提出方法应用于某在轨卫星，太阳敏感器0.5 s间隔测量数据遥测至地面.当星体角速度幅值约为36(°)/s时，直接根据遥测间隔0.5 s太阳敏感器数据进行自旋角速度确定，即将式(16)与(17)中的m=2、n=1与k=1，确定结果如图7～8所示.图7给出了由所确定结果计算得到的自旋轴与星体三轴之间夹角θex、θey与θez的变化情况，由其可知消旋时未对自旋轴方向产生影响，并由消旋后夹角变化获取了消旋所产生的角速度小幅章动特性规律；由图8 角速率确定结果可知，剔除明显野值后(野值数据为大角速度下由于一个自旋周期内敏感器连续有效输出数据过少而保留敏感器视场边缘误差较大测量数据所致)的自旋角速率确定精度约为0.5°(3σ)，且确定结果的均值可明显反映出星体角速度理论消旋降低1(°)/s的变化量.

图6 星体自旋角速率Fig.6 Spinning angle rate

图7 消旋前后自旋轴与星体系三轴夹角Fig.7 Separation angles between spinning axis with satellite body axis respectively

图8 星体消旋前后自旋角速率Fig.8 Spinning angle rate fore-and-aft despinning

当星体角速度消旋降至约为3(°)/s时，若直接采用0.5 s间隔太阳敏感器数据已无法实现自旋角速度高精度确定，因此取式(16)、(17)的m=2、n=1与k=4，确定结果如图9～10所示.由图9三轴角速度变化曲线了解到自旋时动量轮启动一定角动量偏置后的星体复杂自旋运动规律；根据图10确定的角速率可知实际测量误差约为0.8(°)/s(3σ)，且确定结果的均值能明显反映出星体角速度消旋所降低的0.3(°)/s变化量.

图9 消旋前后自旋角速度Fig.9 Spinning angle velocity fore-and-aft despinning

图10 星体消旋前后自旋角速率Fig.10 Spinning angle rate fore-and-aft despinning

3 结 论

本文根据卫星高速稳定自旋时太阳矢量在星体下变化规律分析，提出了基于星体系下太阳矢量序列变化量计算星体自旋轴方位及转速大小的自旋角速度确定方法，并且通过自旋角速度确定误差分析，获取了确定误差与实际角速率、敏感器测量数据间隔及自旋轴与太阳敏感器光轴夹角的关系，并由此得出当太阳矢量与敏感器光轴平行时则无法对自旋角速度进行确定；根据确定误差影响关系结论，给出了随自旋转速相应调整太阳矢量变化信息计算的策略，实现了不同自旋角速度下的高精度自旋角速度确定.该方法仅依赖太阳敏感器测量，算法实现简单，数学仿真验证及工程实际应用表明可解决大角速度姿态异常时测量信息匮乏时系统能源获取状态评估、消旋与进动控制策略制定的姿态信息输入及实施评估等问题.

[1] 徐福祥. 用地球磁场和重力场成功挽救风云一号(B)卫星的控制技术[J]. 宇航学报, 2001, 22(2): 1-11.

XU F X. Technique of successful rescue of FY-1B meteorological satellite by using the magnetic field and the gravitational field [J]. Journal of Astronautic, 2001, 22(2): 1-11.

[2] 耿长福. 航天器动力学[M]. 中国科学技术出版社，北京, 2006.

[3] 王新民, 张俊玲, 袁军, 等. 欠驱动三轴稳定卫星的消旋和进动控制技术[J]. 空间控制技术与应用, 2014, 40(3): 14-18.

WANG X M, ZHANG J L, YUAN J, et al. Despinning and precession control for under-actuated three-axis stabilized satellite[J]. Aerospace Control and Application, 2014, 40(3): 14-18.

[4] 王大轶，李铁寿，陈德祥. 科学双星自旋轴姿态漂移的仿真分析[J]. 航天器工程, 2007, 16(2):13-15.

WANG D Y， LI T S，CHEN D X. Simulation analysis for attitude drift of spin Satellite in Double Star Project[J]. Spacecraft Engineering, 2007, 16(2):13-15.

[5] 屠善澄. 卫星姿态动力学与控制[M]. 宇航出版社，北京, 2001.

[6] IWATA T, YOSHIZAWA T, HOSHINO H, et al. Precision attitude and orbit control system for the advanced land observing satellite[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit. Washington D.C.: AIAA, AIAA 2003-5783.

[7] 王淑一, 刘祥, 陈超. 资源三号卫星控制系统概述及在轨验证[J]. 空间控制技术与应用, 2015, 41(2): 1-5.

WANG S Y, LIU X, CHEN C.Overview of control system and on-orbit test for ZY-3 satellite [J].Aerospace Control and Application, 2015, 41(2): 1-5.