基于Zc参数的HP耐热合金高温蠕变及持久寿命的预测方法

李会芳，赵 杰，程从前，闵小华，曹铁山，许 军

(大连理工大学 材料科学与工程学院，辽宁 大连116024)

随着科技的发展和工业需求的不断增长，高温合金以其优良的抗蠕变性能与组织稳定性能[1]，在航空航天的发动机、核工业的高热部件和发电厂的燃气轮机等心脏部位获得大量应用[2-3]。随着材料服役年限的不断增长，高温合金的蠕变变形量、稳定性和可靠度，是生产设备在实际工作过程中需要参考的重要指标。如何对高温合金的蠕变变形性能进行合理、准确和快速评价，以保证其在实际工作过程中的稳定和安全，是当前工作的重点。但由于实际材料的服役年限往往在几千小时甚至上万小时，直接对材料进行同等环境条件实验是不可行的，这就需要建立适当的本构模型，利用短时间的实验数据，对高温合金长时间的高温蠕变变形和持久寿命进行可靠的预测与评估。

在过去的几十年中，前人提出了很多有关高温蠕变变形和持久寿命的预测方法[4-9]。Larson和Miller于1952年提出了Larson-Miller参数方法(L-M参数法)[10]，该方法是通过归一化时间和温度，利用高于设计需求恒定温度和恒定应力下的持久数据外推设计应力下的寿命，帮助人们解决了很多工程问题。但是该方法在预测精度上一直存在争议，在实验数据比较充足的情况下，根据高于实际服役环境的条件下获得实验数据拟合外推时，才能够得出较为准确的预测。

Evans于1982年提出了θ投影法，该方法在过去的几十年中帮助人们成功预测了一些高温耐热材料的蠕变变形[11-13]，该方法是将蠕变过程看作仅仅由“材料的软化过程”和“材料的硬化过程”两部分组成[14]。通过θ参数与应力和温度的关系，利用高温、高应力的短时蠕变数据来预测材料的长时蠕变数据。但是由于客观实验材料的组织性能的波动性[15]，试样尺寸的波动性和实验过程中实验条件的波动性会直接反映到实验数据上，这就会导致θ参数的数值存在很大的不确定性，从而直接影响长时蠕变数据预测的准确性。本课题组曾对实验数据的分散性作了详细的研究与讨论[15-16]。Prager提出的Ω法是根据蠕变变形速率来评价材料的高温蠕变变形行为，该方法认为材料的抗蠕变性能随变形量的增加逐渐减小，将Ω看成是温度和应力相关的参数[4]。Ω法虽说已在压力容器和热力管线蠕变变形预测中得到了成功的应用[14]，但是该方法也存在与θ投影法相同的问题，即Ω参数的数值会因实验数据的波动性而存在不确定性。

鉴于此，本工作以HP耐热合金为例，提出了一种基于Zc参数的高温蠕变变形预测方法。由于该预测方法同时利用多条蠕变曲线，即该蠕变变形预测方法的结果是建立在多组实验的基础上，既结合了材料的蠕变信息，又有效降低了材料性能的分散性给预测带来的影响，并且该方法仅利用了蠕变曲线的前半阶段，得到的蠕变变形值与实验结果吻合良好。同时利用此方法对材料的持久寿命进行了预测，并且与材料的实验数据进行了对比，结果表明实验数据点均匀分布于预测主曲线两侧，预测主曲线与实验数据点具有良好的关联性。

1 实验材料与方法

实验材料为离心铸造制备而成的HP耐热合金，组织观察采用JSM-5600LV型扫描电子显微镜，成分分析选用Spectro LAB LAVM10光谱仪。合金的成分组成列于表1中。

表1 实验用HP耐热合金的成分(质量分数/%)Table 1 Chemical compositions of experimental HP heat resistant alloy (mass fraction/%)

蠕变断裂实验在RWS50电子蠕变试验机上进行，实验温度为1000, 980, 950，930℃，外界环境温度为室温，实验应力为32～60MPa，蠕变试样尺寸规格根据GB/T 2039-2012加工，其拉伸段尺寸为φ5mm×25mm。

2 结果与讨论

2.1 HP耐热合金的组织与蠕变实验结果

图1为HP耐热合金的显微组织照片，可以看出，该HP耐热合金是由三部分组成，即奥氏体基体、骨架状共晶组织和晶粒内奥氏体基体上的细小析出相。晶粒内的奥氏体基体中存在大量的弥散析出二次碳化物。本工作中所选HP耐热合金为经过一定时间服役后的材料，骨架状的共晶组织存在一定的粗化，但是仍然保持网状。图2为HP耐热合金的蠕变实验曲线，可以看出，应力和温度越低，稳态蠕变速率持续的时间越长；反之，应力和温度越高，材料的蠕变时间越短。

2.2 Zc参数模型

根据以上实验可以得到不同温度和应力下的高温蠕变实验数据，将获得的蠕变实验数据按蠕变应变从小到大选取ε1,ε2,ε3…εi至少6个蠕变应变，并获得与所选应变对应的蠕变实验时间ti。图3(a)为选取的5%蠕变应变的数据点，可以看出1000℃下，不同应力的数据点存在明显的函数关系；但是不同温度下的数据点由于存在明显的分散性，不容易分析这些数据之间的关联性，利用公式(1)对图3(a)数据点中的温度T和蠕变变形时间ti进行归一化处理，最终得到如图3(b)所示的关系图，不难看出不同温度与不同应力下数据点之间的关系，拟合所有数据点，得到图3(b)中的实线。

图1 HP耐热合金的显微组织 (a)低倍组织；(b)高倍组织Fig.1 Microstructures of HP heat resistant alloy (a)low magnification;(b)high magnification

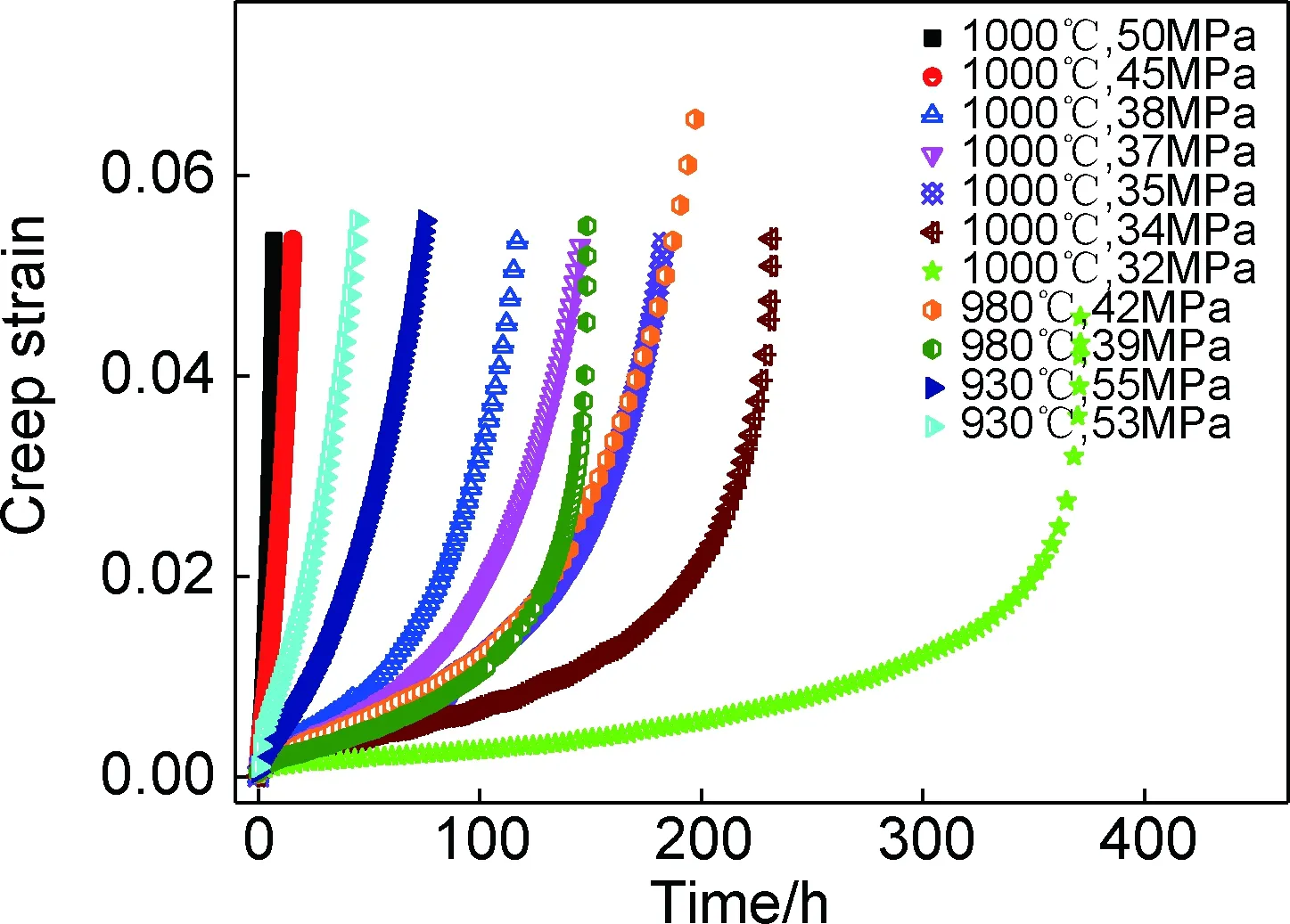
图2 HP耐热合金的蠕变实验曲线Fig.2 Creep experimental curves of HP heat resistant alloy

在每个所选的蠕变应变下，计算得到HP耐热合金的参数P值，其表达式为：

P=10-3×T×(lgti+c)

(1)

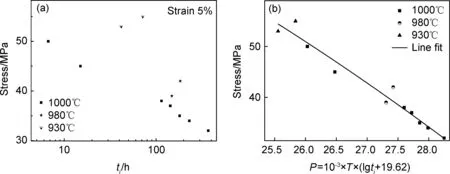
图3 不同蠕变应变下的应力与实验时间关系图 (a)原始数据点；(b)归一化处理后的数据点Fig.3 Relationship between stress and test time at different creep strains (a)original experimental data;(b)experimental data after normalization processing

式中：T为高温蠕变实验温度，K；ti为材料的蠕变实验时间，h；c为材料常数(此处所选的数值为19.62)。

通过图3(b)中的分析，可以得到，不同实验条件下的数据点虽然具有分散性，但是可以通过公式(1)的归一化将所有数据有效地联系起来。同理，利用公式(1)得到其他蠕变应变下的应力-P参数数据点，如图4所示。可以看出随着蠕变应变量的增加，图中的数据点具有明显的平移特征，因此本工作提出了基于Zc参数的高温蠕变变形预测方法。该方法认为不同蠕变应变下，应力与P参数之间存在平行的关系，因此应综合考虑数据之间的关系，建立数学模型：

σ=ai+5P-0.248P2

(2)

式中：ai为任意常数；σ为实验应力；P为参数。

利用所建立的数学模型公式(2)拟合图4中不同蠕变应变下的数据点，得到图4中的拟合曲线。Zc表示每条曲线相对于蠕变应变为0.1%曲线的偏移量。本工作中所选的Zc具体数值为：

Zci=ai-a0.1%

(3)

其中i的取值为0.1%，0.2%，0.5%，1%，2%和5%；a0.1%=67.6083。

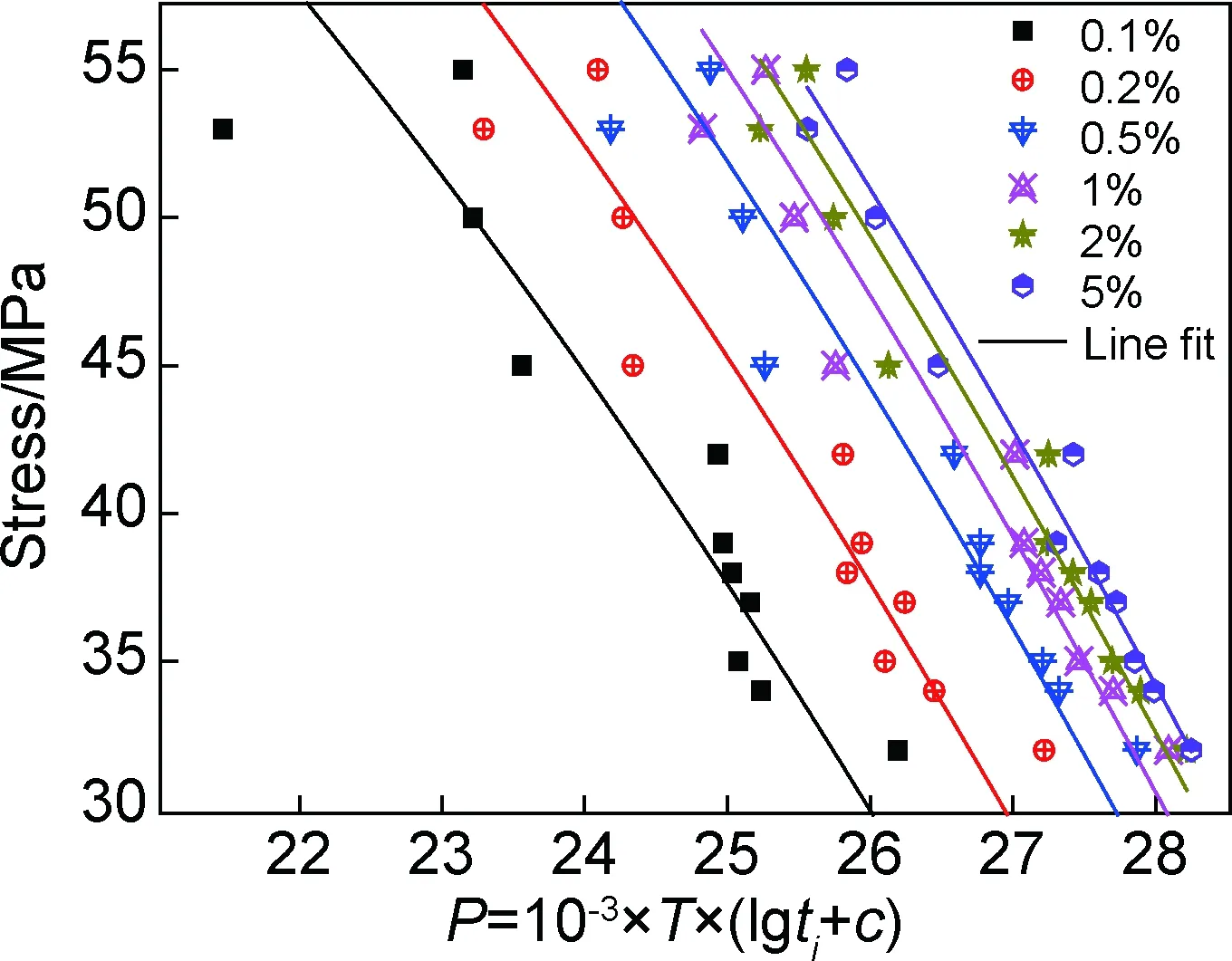
图4 不同蠕变应变下的应力与P参数关系图Fig.4 Relationship between stress and P-parameter at different creep strains

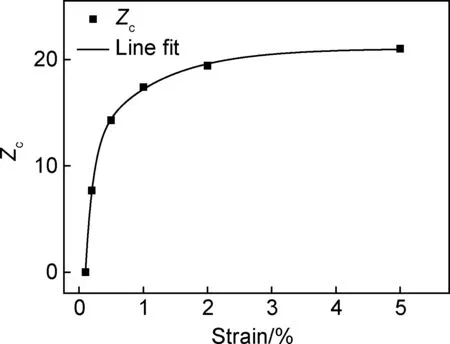
图5 Zc随蠕变应变的变化Fig.5 Variation of Zc with creep strain

从图4中通过关系式(3)得到不同应变下拟合曲线相对于0.1%曲线的Zci值，然后以Zc为纵坐标，蠕变应变为横坐标作图，得到如图5中所示的曲线，通过图5，可以进一步将不同蠕变应变下的数据归一化到一条Zc-应变曲线上，避免了数据分散性给实验分析带来的影响，可以更准确地研究材料的高温蠕变性能。利用图5，可以得到各蠕变应变εi下的Zci值，将得到的Zci值代入式(3)中，求出常数ai，进而将ai值代入式(2)中，得到每个蠕变应变下的具体模型关系式，由该关系式可以预测一定温度和应力下，HP耐热合金的蠕变变形随时间的变化。

2.3 基于Zc参数法的蠕变变形预测结果

图6是基于Zc参数法所得结果与实验结果的比较，可以看出，在不同的实验温度与实验应力下，各蠕变应变下的预测值与实验值符合良好，除个别数据点外，预测结果差异基本上位于3倍误差线(图6中的虚线)范围内。从图6中的右上角数据可以看出，当蠕变时间越长，蠕变三阶段越明显时，预测精度越高；3个蠕变应变下的预测结果误差最大数据点所占比例仅为18.1%；蠕变应变为0.5%和1%时，预测结果差异位于2倍误差线范围内的数据点所占比例达到82%，蠕变应变为5%时，预测结果差异位于2倍误差线范围内的数据点所占比例达到100%。

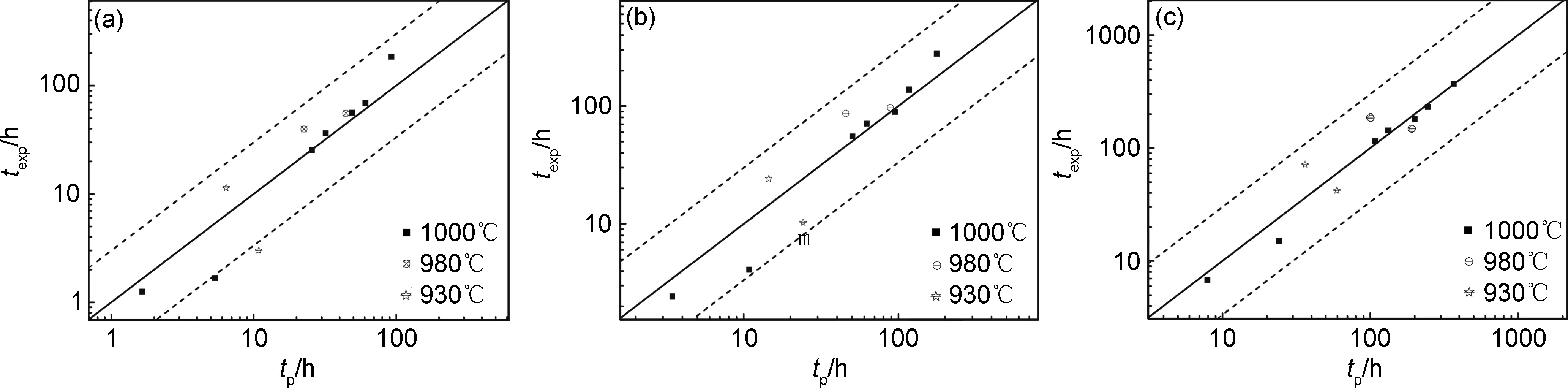
图6 不同蠕变应变下预测值与实验值比较 (a)0.5%;(b)1%;(c)5%Fig.6 Comparison between predicted and experimental results at different creep strains (a)0.5%;(b)1%;(c)5%

2.4 基于Zc参数的蠕变持久寿命预测

根据Zc参数法，选取图5中Zc变化平缓处，且应变较小的蠕变应变作为断裂应变，再根据图4选取该蠕变应变下所对应的断裂主曲线作为预测断裂主曲线。由蠕变断裂实验数据点和预测主曲线可以得到如图7所示的数据图，可以看出，真实蠕变数据点均匀分布于预测主曲线两侧，表明该预测主曲线可以较好地表征HP耐热合金的高温蠕变断裂性能。

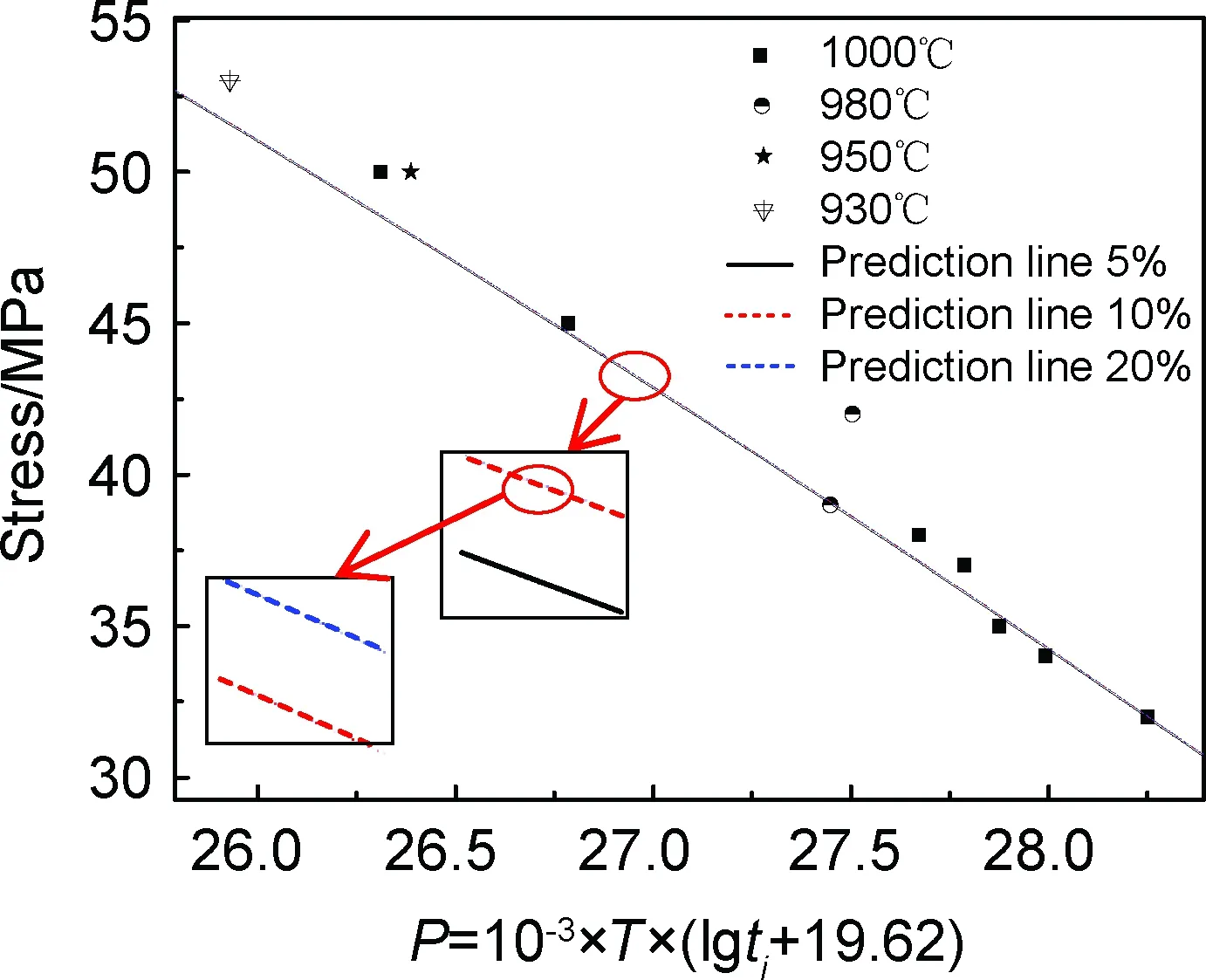
图7 应力-P参数数据点与预测曲线的比较Fig.7 Comparison between the data of stress-P parameter and the prediction line

同时，在图7中还分别列出了蠕变应变为5%，10%和20%时的预测主曲线，可以看出，当图5中的Zc变化平缓时，随着蠕变应变的增加，预测主曲线之间的差异很小，这意味着当选择的断裂应变在某一临界值时，得到的持久寿命之间的差异较小。

本工作设定温度为1000℃，设定应力为32MPa时，结合以上所述的基于Zc参数的持久寿命预测方法，选取应变为5%的公式(2)为预测主曲线，并结合公式(1)可以得到预测持久寿命为367.49h，而实验实际断裂时间为371.18h，预测时间与真实实验时间非常接近。这说明基于Zc参数方法不仅可用于预测高温蠕变变形，同时在持久寿命中也可得到相对稳定的结果。

3 结论

(1)基于Zc参数的高温蠕变变形预测方法，利用短时间的蠕变实验数据，能够较好地预测耐热合金的高温蠕变变形。

(2)利用基于Zc参数的高温蠕变变形预测方法，能够对材料的高温持久性能进行较好的预测,进一步降低了材料性能分散性和实验结果波动性给材料的高温蠕变变形预测带来的影响。基于Zc参数的高温蠕变变形预测方法能够在实验数据存在波动性的情况下，得出比较理想的持久寿命预测结果。

[1] 潘晖，赵海生. 镍基钎料钎焊K465高温合金大间隙接头组织与性能研究[J]. 材料工程，2017，45(5)：86-93.

PAN H，ZHAO H S. Research on microstructure and mechanical properties of wide-gap brazed joints of K465 superalloy using nickel-base brazing filler metal[J]. Journal of Materials Engineering，2017，45(5)：86-93.

[2] 胡春燕，刘新灵，陶春虎，等. 气膜孔分布对DD6单晶高温合金持久性能及断裂行为的影响[J]. 材料工程，2016，44(5)：93-100.

HU C Y，LIU X L，TAO C H，et al. Influence of cooling holes distribution on stress rupture property and fracture behavior of single crystal superalloy DD6[J]. Journal of Materials Engineering，2016，44(5)：93-100.

[3] 王丽丽，李嘉荣，唐定中，等. SiO2-ZrO2陶瓷型芯与DZ125，DD5和DD6三种铸造高温合金的界面反应[J].材料工程，2016，44(3)：9-14.

WANG L L，LI J R，TANG D Z，et al. Interfacial reactions between SiO2-ZrO2ceramic core and DZ125,DD5,DD6 casting superalloys[J]. Journal of Materials Engineering，2016，44(3)：9-14.

[4] PRAGER M. The omega method-an engineering approach to life assessment[J]. Journal of Pressure Vessel Technology，2000，122(3)：273-280.

[5] PARK K S, BAE D S, LEE S K, et al. Creep modeling for life evaluation and strengthening mechanism of tungsten alloyed 9-12% Cr steels[J]. Metals and Materials International，2006，12(5)：385-391.

[6] KURATA Y, UTSUMI H. Applicability of creep constitutive equations to creep curves under constant load[J]. Acta Metallurgica Sinica (English Letters)，2009，11(6)：397-404.

[7] MARUYAMA K, OIKAWA H. Comments on “exponential descriptions of normal creep curves by SGR Brown, RW Evans and B Wilshire”[J]. Scripta Metallurgica，1987，21(2)：233-237.

[8] 于慧臣，董成利，焦泽辉，等. 一种 TiAl 合金的高温蠕变和疲劳行为及其寿命预测方法[J]. 金属学报，2013，49(11)：1311-1317.

YU H C，DONG C L，JIAO Z H，et al. High temperature creep and fatigue behavior and life prediction method of a TiAl alloy[J]. Acta Metallurgica Sinica，2013,49(11)：1311-1317.

[9] Le MAY I. Developments in parametric methods for handling creep and creep-rupture data[J]. Journal of Engineering Materials and Technology，1979，101(4)：326-330.

[10] LARSON F R, MILLER J. A time-temperature relationship for rupture and creep stresses[J]. Transactions of the ASME,1952, 74：765-775.

[11] 江冯，李萍，程从前，等. θ投影法和复合模型在预测耐热钢蠕变行为的比较分析[J]. 材料工程，2015，43(7)：87-92.

JIANG F，LI P，CHENG C Q，et al. Comparative analysis of creep behavior prediction of heat resistant steel based on theta projection and composite model[J]. Journal of Materials Engineering，2015，43(7)：87-92.

[12] ZHAO Y P, GONG J M, YONG J, et al. Creep behaviours of Cr25Ni35Nb and Cr35Ni45Nb alloys predicted by modified theta method[J]. Materials Science and Engineering: A，2016，649：1-8.

[13] HARRISON W, WHITTAKER M, WILLIAMS S. Recent advances in creep modelling of the nickel base superalloy, alloy 720Li[J]. Materials，2013，6(3)：1118-1137.

[14] KIM W, KIM S, LEE C. Long-term creep characterization of Gr. 91 steel by modified creep constitutive equations[J]. Metals and Materials International，2011，17(3)：497-504.

[15] 赵杰. 耐热钢持久性能的统计分析及可靠性预测[M]. 北京：科学出版社，2011.

ZHAO J. Statistical analysis and reliability prediction of the endurance property on the heat resistant steel[M]. Beijing：Science Press，2011.

[16] 赵杰，李东明，方园园. T91/P91 钢持久性能的统计分析及可靠性预测[J]. 金属学报，2009，45(7)：835-839.

ZHAO J，LI D M，FANG Y Y. Statistical analysis and reliability prediction of creep rupture property for T91/P91 steel[J]. Acta Metallurgica Sinica，2009，45(7)：835-839.