两绝缘线悬挂两带电小球静止时的不变量

赵 军 李 力 蔡源园

(1. 重庆市清华中学,重庆 400054; 2. 重庆市融汇清华实验中学,重庆 400054)

如图1(a)所示,两绝缘细线悬挂两同号带电小球,如果静止时两球位于同一高度,容易证明m1tanθ1=m2tanθ2,即m·tanθ是不变量.于是偏角大小与两球带电荷量无关,且质量大则偏角小,反之亦然,这是众所周知的结论.

进而考虑如图1(b)的两细线长度相等的情况,偏角是否仍然仅与质量存在上述关系?

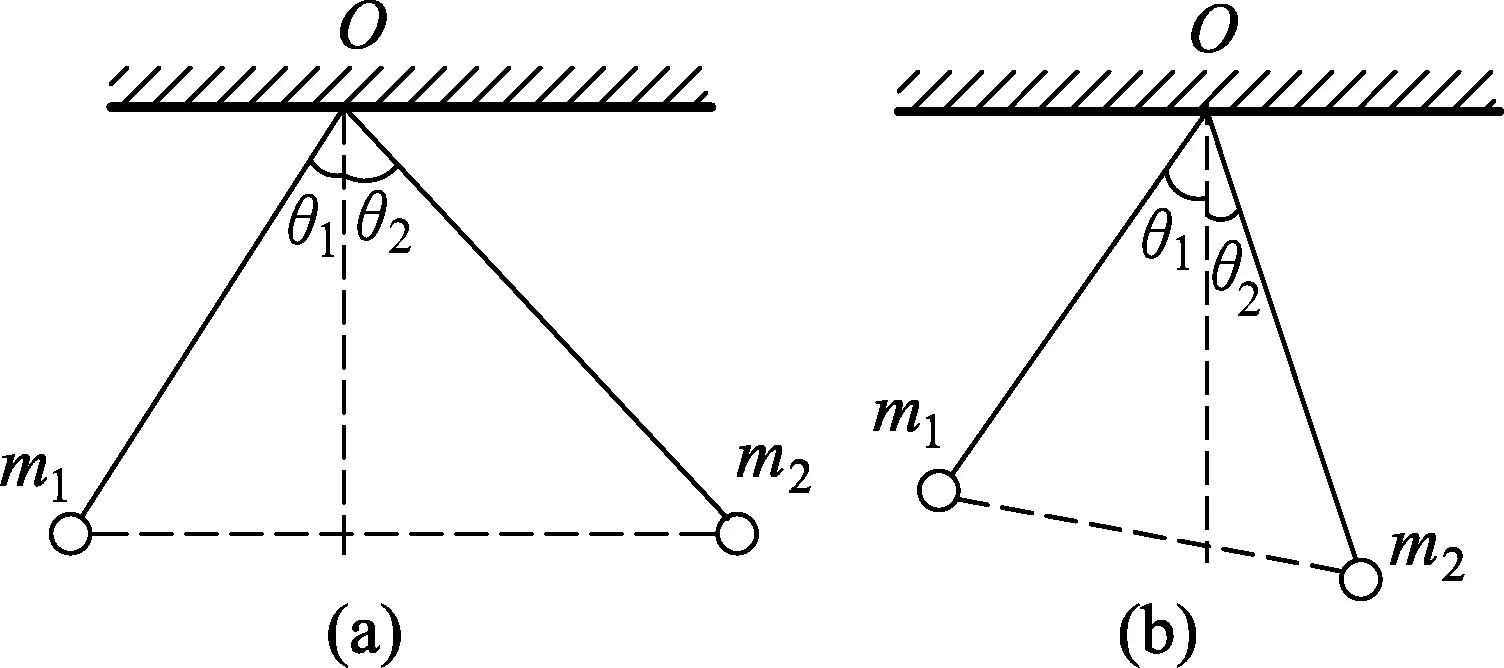
图1

对此也不难用平衡条件(比如拉密定理)推得m1sinθ1=m2sinθ2,即m·sinθ是不变量.同样有“偏角大小与两球带电荷量无关,且质量大则偏角小,反之亦然”的结论.

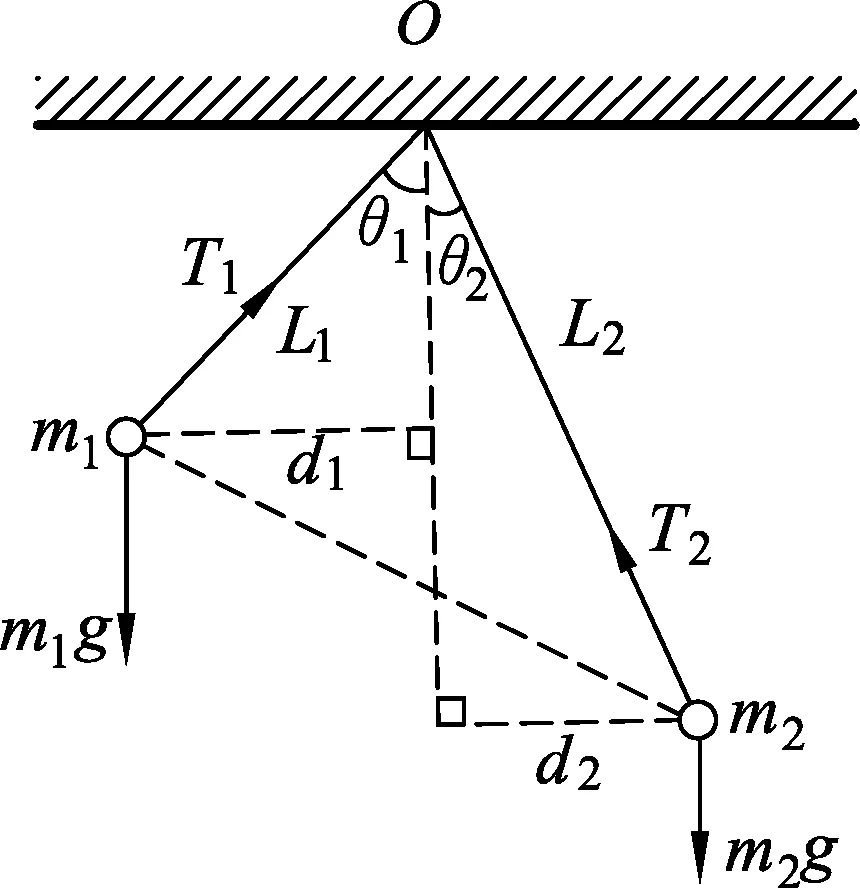
图2

于是不禁要问:如果线长不等(分别为L1,L2)且静止时两球亦不在同一高度,如图2所示,那么还有此结论么?这种一般情况下不变量又是什么呢?

这时再逐个研究单个小球的平衡,就稍嫌繁琐了．因两小球均平衡,则体系所受外力对O点的力矩代数和应该为0．两球间的库仑力是一对内力,而线对球的拉力均过O点从而力矩为0,故有m1L1sinθ1=m2L2sinθ2,可见不变量是m·Lsinθ.虽然偏角大小仍然与两球带电荷量无关,但是“质

量大则偏角小”不再成立,因为还与线长有关．容易看出,在静止时两球位于同一高度或线长相等的条件下,不变量m·Lsinθ分别转化为m·tanθ、m·sinθ,这说明图1的两种情况是特例.

由于线长不等,同号两球排斥作用产生的偏离程度,显然不能用线与竖直方向的偏角大小来表示了．注意到d=Lsinθ,故不变量可写成m·d,d为静止时小球到过悬点O的竖直线的距离(如图2),它正是这种一般情形中代替偏角描述小球偏离程度的几何量.所以,得到如下普遍成立的定理.

定理:两绝缘线同悬点悬挂两带电小球静止时,小球质量与其到过悬点的竖直线的距离的乘积m·d是不变量,与小球带电荷量无关．

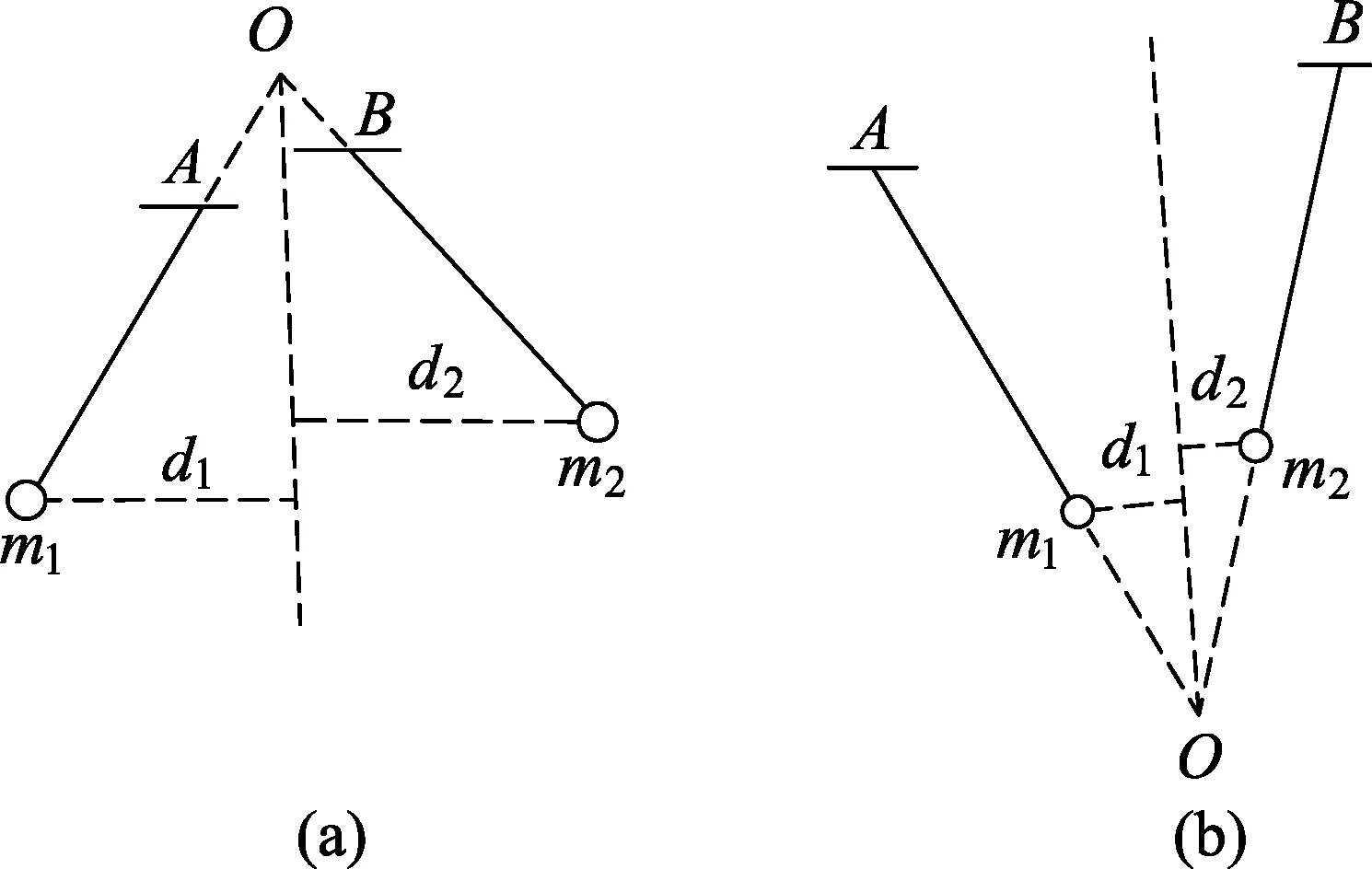
此结论还可推广,当两同号带电小球悬挂点不同甚至不等高时[如图3(a)],或者两异号带电小球相吸引的情况[如图3(b)],上述结论也是成立的.因为取两线延长线的交点为O点,则前面的证明过程同样是成立的.不过必须提醒的是,这时d应该是静止时小球到过O点竖直线的距离(如图3)．这样,在图3(a)中因d1m2;图3(b)因d1>d2,则m1

图3