双光子聚合加工系统的误差建模及辨识
2018-03-21林洁琼
林洁琼,高 瑞,靖 贤,谷 岩
(长春工业大学 机电工程学院,吉林 长春 130012)
1 引言
目前,针对三维微纳结构的制造工艺方法,国内外学术界现有的研究中,普遍认为双光子聚合(Two-photon polymerization,以下简称TPP)加工方法是最有效、最有发展前途的工艺方法[1]。三维超材料能否在重要领域的应用获得成功,关键在于如何保证双光子聚合加工系统的精度,从而获得高质量的微纳结构。
在研究微结构加工的误差影响过程中,文献[2]提出了一种新的方法,自适应数学表达模型(SMEM),描述了基于非均匀有理B样条(NURBS)机床误差。用体对角线多步运动测得位移误差。文献[3]针对旋转轴的几何误差模型提出了“误差第一模型”和“运动第一模式”,对回转轴的几何误差进行了辨识分析。为系统、快速方便地测量五轴数控机床2个旋转轴所有的几何误差项,文献[4]提出一种基于球杆仪测量的六圈法几何误差辨识方法。文献[5]提出机床几何误差参数辨识的7线法,基于此系统实现误差数据的采集和机床几何误差参数的快速辨识。文献[6]针对国内外对于非正交数控机床的斜摆轴B轴误差辨识研究较少问题,基于多体系统理论建立非正交五轴数控机床运动误差模型。此外,文献[7]研究了一种根据被加工零件的三轴机床运动误差辨识新方法。文献[8]基于平面正交光栅方法,提出了多步测量方法。文献[9]利用三面对角线矢量测量的方法,并测量了三个运动轴的定位误差,从而实现了机床误差参数的辨识。
为减少系统运动误差,进一步提高微纳结构的加工精度,研究双光子聚合加工系统的误差,根据多体理论建立误差模型,并通过实验测量出误差项以及误差项的主要来源,运用MATLAB软件对误差数据进行分析,研究几何误差的影响因素,同时利用改进九线法对双光子聚合加工系统的误差进行参数辨识,对提高加工精度和提升微纳结构的质量有重要意义。
2 双光子聚合加工系统误差分析
2.1 加工系统误几何误差分析
在TPP微制造过程中,激光功率、曝光时间、材料以及工作台定位精度等都是影响双光子聚合加工的因素。在影响双光子聚合加工系统精度的诸多误差中,几何误差所占据的百分比较大。双光子聚合加工系统在运动过程中,会存在21项几何误差项,该运动时产生的几何全部误差元素具体,如表1所示。

表1 双光子聚合加工系统的几何误差项和表达式Tab.1 Geometric Error Terms and Expressions of the Two Photon Polymerization Processing System
2.2 加工系统误二维振镜误差分析
从理论研究出发,激光扫描形式大致主要模式分为两种:(1)物镜前扫描方式;(2)物镜后扫描方式,扫描方式主要取决于反射镜和聚焦物镜的位置关系,物镜前扫描会出现枕形失真与桶形失真的复合型,物镜后扫描会出现x向的枕形失真。二维振镜工作原理,如图1所示。根据扫描角度的范围变化,理论的轮廓线应为长方形。显然,扫描轨迹最大的轮廓线为双曲线,这种误差被称为枕形误差,如图2所示。从上式可知,x方向扫描出来的轮廓误差是x轴振镜和y轴振镜偏转的角度共同决定的,y方向扫描出来的轮廓误差是y轴振镜偏转的角度β息息相关。着重分析运动副的误差和二维振镜误差产生的原因,最后得出影响加工系统精度需要重点研究的误差项,为后续的系统几何误差建模打下基础。
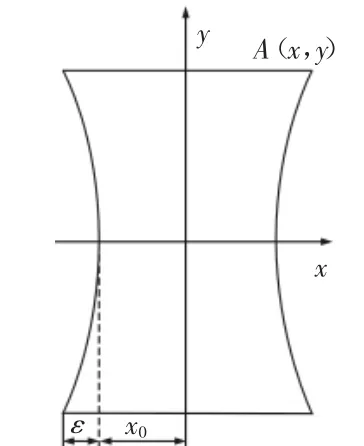
图2 二维振镜枕形失真Fig.2 Two Dimensional Vibration Mirror

图1 二维振镜扫描原理图Fig.1 Two Dimensional Scanning Principle Diagram
3 双光子聚合加工系统几何精度的测量
3.1 搭建实验测量系统及空间规划
在试验中,由于激光干涉仪具有测量较高精度、稳定性高、速度快、抗干扰能力强、操作方便、数据自动处理等优点,故采用由Renishaw生产制造XL-80激光干涉仪且基于光的干涉原理的测量技术对运动进给轴进行定位误差和直线度误差测量,利用光线回程光程差的变化得到误差变化数值。运动台的x轴的量程(0~200)μm,y轴的量程(0~200)μm,z轴的量程(0~200)μm。确定测量间距并编制程序,采用停顿3s来采集每段数据,安装激光干涉仪,并调整测量轨迹,使其达到最佳状态进行测量。以x轴为例开展试验研究,介绍其测量过程,激光干涉仪检测x轴的定位误差和直线度误差现场布置,如图3、图4所示。

图3 x轴y向和z向直线度误差测量现场Fig.3 x Axis y Direction and z Direction Straightness Error Measurement on the Spot

图4 线性定位误差测量现场Fig.4 Linear Positioning Error Measurement Site
3.2 几何误差的测量数据分析
运行程序后,对设定的轨迹进行测量,得到x轴的单项误差数据,经过MATLAB处理后,定位误差和直线度误差数据如图所示,横坐标表示运动轴的位移,纵坐标表示相对应的位置的几何误差,如图5所示。根据激光干涉仪的测量,对测量数据进行分析和处理,从x轴的三个点的位置测量的结果可以发现,x轴的定位误差从0μm到150μm的过程中,在50μm到100μm趋于稳定,上下波动除了个别变化大,最大定位误差0.17μm。x轴y方向直线度误差在0μm到40μm持续增加0.14μm范围内变化,在50μm到100μm趋于下降,之后逐步稳定。x轴z方向直线度误差从30μm到110μm的过程中趋于波动稳定,在110μm之后误差持续增加。
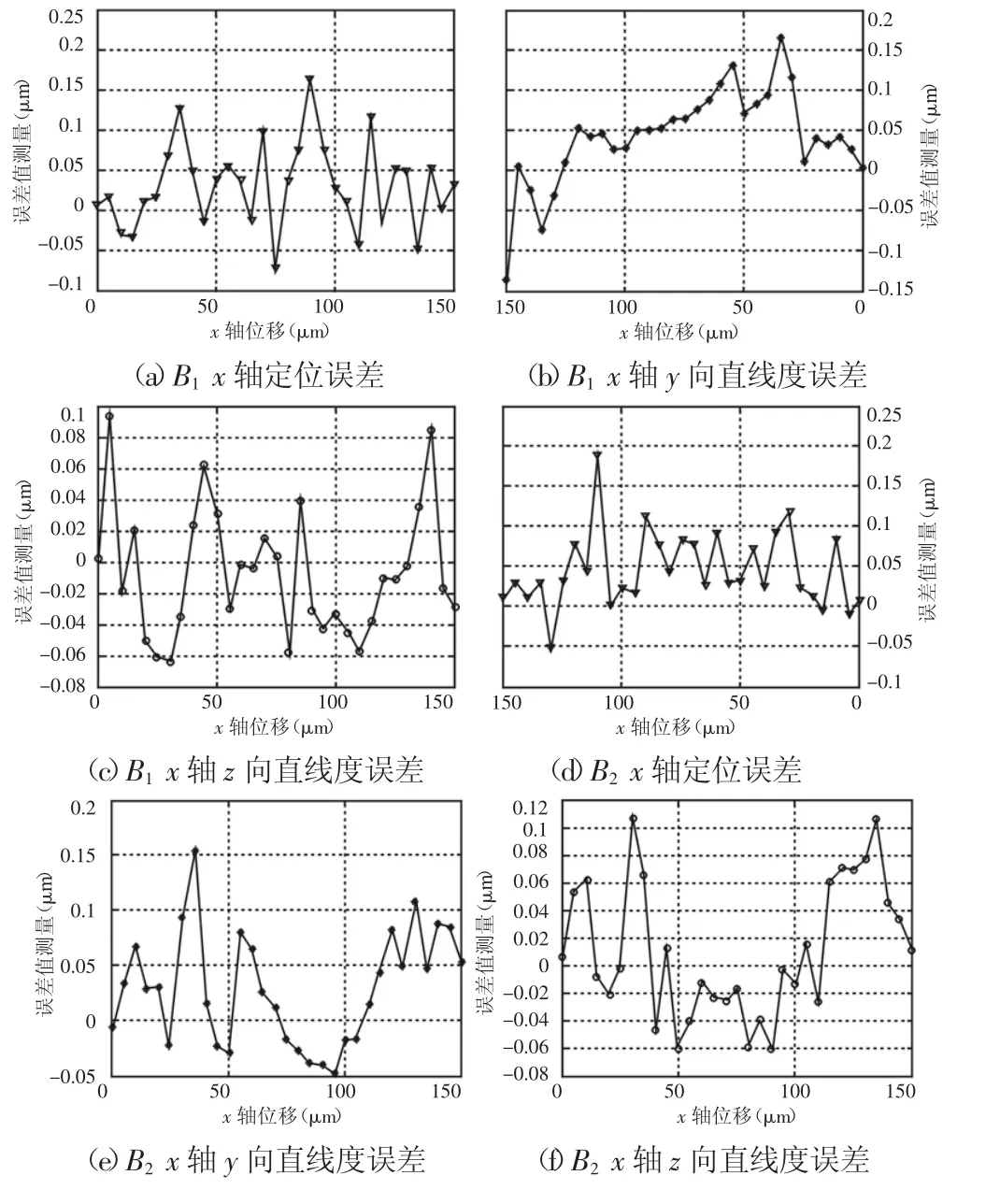

图5 误差测量结果Fig.5 Results of Error Measurement
4 双光子聚合加工系统几何误差建模与辨识
4.1 双光子聚合加工系统误差建模
系统的几何误差包括工件装夹误差、磨损误差、运动副误差、系统非刚体误差等。建立该机床综合误差模型,要基于刚体假说,重点考虑影响较大的运动副误差,忽略工件装夹和刀具安装、磨损引起的误差。x轴的坐标变换矩阵如下。x轴相对于隔振台相邻体的理想静止、运动和实际静止、运动的齐次变换矩阵分别为:

取刀具坐标系Ot-xtytzt中刀具加工点Pt,用矢量表示Pt=(xt,yt,zt,l)T;工件坐标系 Ow-xwywzw中工件被加工点 Pw,用 Pw=(xw,yw,zw,l)T矢量表示。典型体间都会建立自身的坐标系,为了简化,我们需将在平动、转动过程中产生的误差,通过刀具加工点和工件被加工点的位置矢量都统一转化到机床床身坐标系,从而推导出误差模型。用Pto,Pwo位置矢量分别表示刀具加工点和工件加工点转化到机床床身坐标系。则在系统实际加工过程中,刀具加工点在机床坐标系O0-x0y0z0中的齐次坐标变换矩阵为:
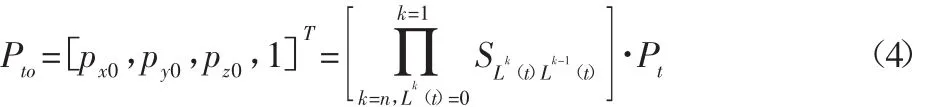
由于刀具实际加工点不可能完全重合于被加工件的理论加工点,则设Vtw为系统的空间几何误差模型:


最终可得到双光子聚合加工系统的空间几何误差模型为:根据双光子聚合加工系统的运动结构特点,确定了刀具分支和工件分支,将系统主要组成部分简化,利用齐次坐标变换原理,对于各个运动轴系之间的相互关系从低阶到高阶依次推导,建立了双光子聚合加工系统的几何误差模型,为双光子聚合加工系统的误差辨识提供了理论基础。
4.2 双光子聚合加工系统误差辨识
用改进的九线法误差辨识法对双光子聚合加工系统的误差进行辨识,改进九线法不仅局限于传统九线法的应用范围,可以通过增加线数的测量,有效降低了偶然因素对辨识结构的影响,可更深入提高求解的稳定性,能对机床精度设计与工艺优化具有一定指导意义,提高辨识算法的鲁棒性[10]。此误差辨识的数学模型为:

式中:“+”—矩阵的广义逆。
根据激光干涉仪所测数据和MATLAB软件分析,将数据带入式(7)中计算,可以辨识出x轴运动部件的空间姿态误差,如图6所示。从图6可以发现,在x轴运动的情况下,定位误差和直线度的误差较大,影响因素比例更高。同理,可以用同样的方法把y轴和z轴定位误差和直线度误差测出来,并辨识出其他几项误差,在此不一一列举。所分析出的定位误差在(-0.05~0.15)μm 范围内波动,y向直线度误差在(-0.05~0.15)μm 范围内波动,z向直线度误差在(-0.05~0.1)μm 范围内波动。

图6 误差源辨识结果Fig.6 Error Source Identification Results
5 结论
双光子聚合加工是大面积超材料最有潜力的加工方式,近年来在航空电子、医疗器械、传感器技术等领域受到广泛关注,以提高双光子聚合加工系统的精度为研究目标,主要针对系统的误差建模、误差辨识和主要误差影响因素等内容展开研究,主要结论如下:(1)分析了双光子聚合加工系统各组成部分的误差项及系统误差的主要来源,结合双光子聚合加工系统的运动关系,对误差进行了分类,并着重分析了运动副的误差和二维振镜误差产生的原因,最后得出影响加工系统精度需要重点研究的误差项。(2)搭建实验测量系统,并通过激光干涉仪对加工系统进行了几何误差测量,通过测量平台三条运动轴的定位误差与直线度并结合误差辨识技术,方便地分离出平台的几何误差元素。进一步实施误差推算,得到了误差模型所需误差项数值,为后续误差补偿提供基础,所分析出的定位误差在(-0.05~0.15)μm 范围内波动,y向直线度误差在(-0.05~0.15)μm 范围内波动,z向直线度误差在(-0.05~0.1)μm 范围内波动。
[1]董贤子,陈卫强,赵震声.飞秒脉冲激光双光子微纳加工技术及其应用[J].科学通报,2008,53(1):1-13.(DongXian-zi,ChenWei-qiang,ZhaoZhen-sheng.Femtosecondlasertwophoton micro nano processing technology and application[J].Science Bulletin,2008,53(1):1-13.)
[2]Hea Z,Fub J,Zhanga X.A uniform expression model for volumetric errors of machine tools[J].International Journal of Machine Tools and Manufacture,2016(100):93-104.
[3]Dinga S,Huanga X.Identification of different geometric error models and definitions for the rotary axis of five-axis machine tools[J].International Journal of Machine Tools and Manufacture,2016(100):1-6.
[4]付国强,傅建中,沈洪垚.五轴数控机床旋转轴几何误差辨识新方法[J].浙江大学学报:工学版,2015,49(5):848-857.(Fu Guo-qiang,Fu Jian-zhong,Shen Hong-yao.Rotation axis geometric error,a new method for identifying five axis CNC machine tool[J].Zhejiang University Journal:Engineering and Technology Edition,2015,49(5):848-857.)
[5]王移风,汪琛琛,曹衍龙.数控机床几何误差的辨识研究[J].机械设计与制造,2014(2):136-139.(Wang Yi-feng,Wang Chen-chen,Cao Yan-long.Identification of geometric errors of CNC machine tools[J].Mechanical Design and Manufacture,2014(2):136-139.)
[6]范晋伟,王志远,唐宇航.非正交五轴数控机床旋转轴误差辨识方法的研究[J].组合机床与自动化加工技术,2015(1):71-74.(Fan Jin-wei,WangZhi-yuan,Tang Yu-hang.Non orthogonal five axis NC machine tool spindle error identification method of[J].Modular Machine Tool and Automatic Manufacturing Technique,2015(1):71-74.)[7]Mostafa Pezeshki1,Arezoo B.Kinematic errors identification of three-axis machine tools based on machined work pieces[J].Precision Engineering,2016(43):493-504.
[8]Du Z,Zhang S,Hong M.Development of a multi-step measuring method for motion accuracy of NC machine tools based on cross grid encoder[J].International Journal of Machine Tools and Manufature,2010,50(3):270-280.
[9]Bui C.B,wang H.J,Lee C.H.Three-face step-diagonal measurement method for the estimation of volumetric positioning errors in a 3D workspace[J].International Journal of Machine Tools and Manufacture,2012(60):40-43.
[10]田文杰,牛文铁,常文芬.数控机床几何精度溯源方法研究[J].机械工程学报,2014,50(7):128-135.(Tian Wen-jie,NiuWen-tie,Chang Wen-fen.Research on the tracing method of geometric precision of CNC machine tools[J].Journal of Mechanical Engineering,2014,50(7):128-135.)
