基于压缩感知理论的运动声源识别方法研究

李会超，刘 鹏，刘志红，仪垂杰

（青岛理工大学 机械工程学院，山东 青岛 266033）

1 引言

目前的各种压缩方法在处理现实问题时会出现不足和缺陷，压缩感知理论应运而生。由于压缩感知理论在数据处理领域具有突出优势，所以一经问世就引起了相关领域的广泛关注，该理论指出了将模拟信号直接采样压缩为数字形式的有效途径，可以实现信息的直接采样。从理论上讲，冗余在所有的信号中都会存在，因此任何信号都具有可压缩性，只要能找到合适的稀疏基，就能够对信号进行有效地压缩采样，然后通过优化计算重建出原始信号。压缩感知理论突破了传统方法对信号压缩采样的限制，利用信号的稀疏性将算法的复杂性问题彻底解决，为信号后期的处理奠定了基础。在运动声源的识别过程中，从图像、语音信号的数据获取到传递，再到数据处理，每个过程都涉及到大量的数据。针对研究中大量数据存在导致处理过程复杂的问题，提出了在声源识别的数据处理过程中运用压缩感知理论，并通过实验证明了通过压缩感知处理后的数据可以更清晰的实现声源识别。压缩感知流程图，如图1所示。

图1 信号压缩感知流程图Fig．1 Signal Compressed Sensing Flow Chart

2 时变信号稀疏化

由压缩感知理论描述可知，如果信号在某个变换域上是可压缩的，那么原来的信号就可以通过一个观测矩阵实现从高维信号到低维空间的转换。然后在求解优化问题的基础上，将原始信号从少量的稀疏表示中重构出来。信号稀疏定义是：信号x∈Rn×1，对于正交基（Ψi：i=1，2，3…n，Ψi∈Ψ），信号在基上的投影（即变化因子）为 Si=＜x，Ψi＞，若存在某个正实数 0＜p＜2，以及正实数 E＞0，使≤E，则称信号在变换域Ψ上是稀疏的；从广义上讲，如果信号s中存在K个非零元素，则称信号x为K的稀疏信号。

信号x（t）的稀疏性或可压缩性是应用压缩感知理论的重要前提，因此，首先要知道信号的稀疏表示。傅里叶变换可以有效地稀疏表示时变信号，离散傅里叶变换（DFT）是傅里叶变换在时域和频率都呈离散的形式，将信号的时域采样变换为其DFT频率采样。对于 N 点序列｛x［n］｝0≤n≤N的离散傅里叶变换为：

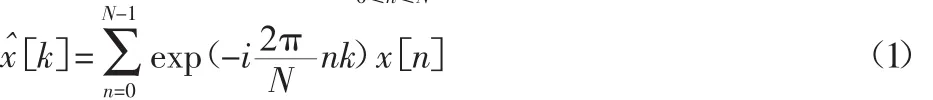
此，DFT矩阵具有正交性，能稀疏完整地表示时变信号。

3 时变信号测量矩阵

3.1 测量矩阵的特性分析

压缩感知过程的本质是将一个信号在测量矩阵的基础上进行处理，实现由高维空间到低维空间的映射转换。因为有些情况下信号的恢复程度受限制，为了尽可能精确的从测量值中恢复原始信号，E．Candès和T．Tao提出压缩感知矩阵必须满足约束等距性条件（RIP），并给出了相关定义。对于稀疏度为K的稀疏信号α，RIP定义如下：

式中：矩阵Θ=ΦΨ为感知矩阵，δK—K阶约束等距常数，如果δK∈［0，1），那么可以判断出这个感知矩阵可以满足约束等距性条件。

若一个感知矩阵是已经确定好的，要想运用公式或者数学方法来验证这个矩阵能不能满足约束等距性的条件非常困难，为了解决这一问题，Baraniuk在之后提出了约束等距特性的等价条件，也就是压缩测量矩阵Φ与稀疏表示矩阵Ψ不相关，同样可以满足重构的要求。相关的系数定义为：

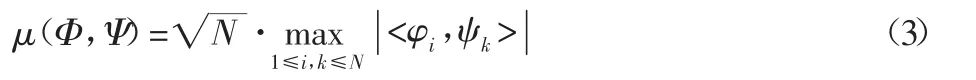
Φ与Ψ的列向量之间的相关性由相关系数进行了定义，Φ与Ψ之间的相关系数取值范围为两者之间的相关系数与原始信号被压缩测量值所携带的信息量有密切关系，相关系数越小则携带的信息量就越大，准确重构原始信号的可能性也就越大。

要验证一个矩阵是不是能作为压缩测量矩阵可以用约束等距性条件和相关特性检验，但是不能由这两个约束性来指导压缩测量矩阵的构造。

3.2 随机观测矩阵的选择

在传感矩阵中的大多数的元素来自独立同分布的随机变量。而正因为这些元素服从一些预定的分布，所以其产生的随机矩阵满足约束等距性的概率也会比较高，所需的测量次数也随之减少。随机高斯、伯努利或部分傅里叶矩阵等已经通过实验证明，均能满足约束等距性，且所用的测量次数与稀疏度成线性关系。

现将一帧512点语音信号作为实验样品，通过相同数据恢复算法，在观测矩阵和压缩比不同的情况下比较数据，得到结果，如图2所示。其中，USE、RSE、RST分别表示随机高斯观测矩阵、随机贝努利观测矩阵、部分傅里叶矩阵，并作为观测矩阵，再经过BP（基追踪算法）进行信号重构，并得到重构以后的重构语音信噪比曲线图，如图2所示。

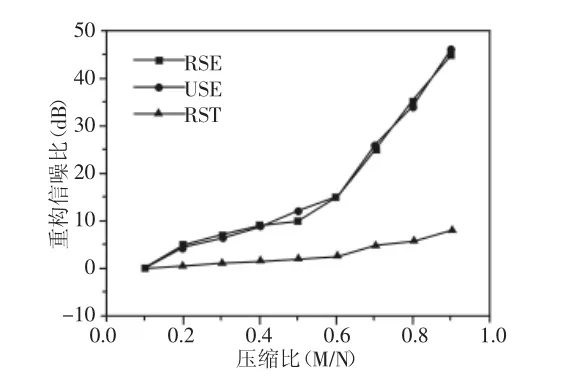
图2 基于不同观测矩阵重构语音信信噪比曲线Fig．2 Reconstructed Speech Signal to Noise Ratio Curve Based on Different Observation Matrix

从图2的曲线比较中可得：当观测矩阵选择USE、RSE、RST时，在压缩比M/N增大的同时，语音的重构信噪比也不断提高；相比而言，选用RST作为观测矩阵时重构语音性能较差。考虑到随机高斯矩阵的优越性，而且是目前最常用并能同时满足RIP约束性的观测矩阵，所以在后期的实验数据处理阶段将以随机高斯矩阵（USE）作为观测矩阵。

4 运动声信号重构算法选择

下面以四种算法分别在采样率为（0．1～0．8）时的峰值信噪比（PSNR）、相对误差（Relative-error）、匹配度（Mat-rat）以及运行时间（Time）的曲线图进行直观比较分析，如图3、图4所示。

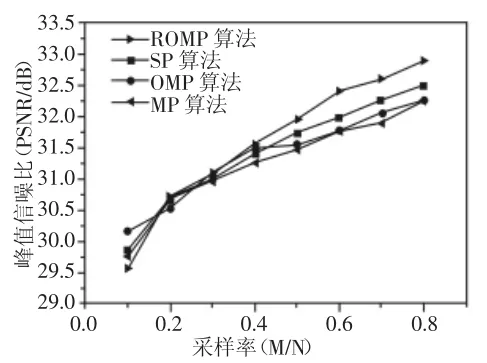
图3 峰值信噪比曲线图Fig．3 Peak Signal to Noise Ratio

图4 相对误差曲线图Fig．4 Relative Error Curve

由图3可以看出，当采样率较低时四种算法的峰值信噪比都比较低。随着采样率的增大，各种算法的峰值性噪比也逐渐增大，其中以ROMP算法增大的速率最快。采样率较高时，ROMP算法的PSNR值和其它三种算法相比明显较高，因此在采样率较高的情况下选用ROMP算法进行信号重构最为合适。峰值信噪比较低时，这几种算法都适用。由图4中曲线可以得出，当采样率较低时，相对误差都很接近。而且可以看出以上四种算法的相对误差在采样率不断提高的同时逐渐减小。由此可以得出算法的误差性能可以通过采样数目的增加得到改善。从图中可以明显看出当采样率较高时，ROMP算法的相对误差下降速度最快。匹配度与运行时间曲线图，如图5、图6所示。

图5 匹配度曲线图Fig．5 Matching Degree Curve

图6 运行时间曲线Fig．6 Running Time Curve

从图5中曲线可以看出，四种算法的匹配度都比较高，但是ROMP算法的匹配度随着采样率的上升趋势更明显，由此看出同等情况下ROMP算法优于其它三种算法。

从图6可以看出，SP算法的运行时间太长，而MP、OMP、ROMP三种算法的运行时间变化较小，且三种算法的时间差距不大。

统筹考虑以上所有分析结果，ROMP算法无论在重构质量还是在重构的速度方面都是实现信号重构应该首先考虑的选择。

5 实验测试

5.1 识别实验

分别以500Hz、1kHz、3kHz的声源进行测试，每个频率做三组实验，最后对同频率的实验结果以偏移距离、区域面积作为参考因素进行比较、分析。

实验1通过声像仪进行声源识别，针对三个频率，得到的声场图，如图7所示。

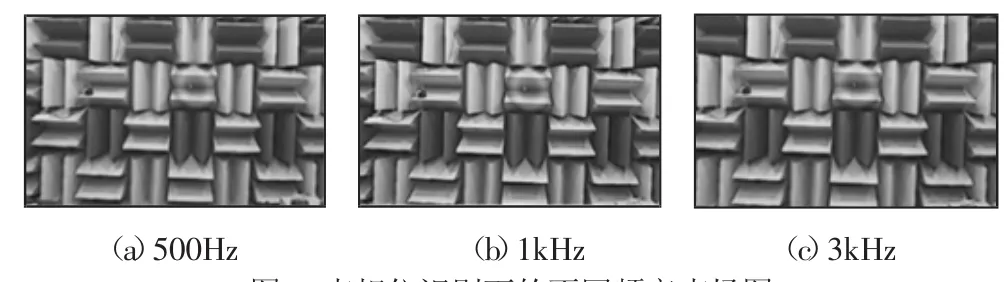
图7 声相仪识别下的不同频率声场图Fig.7 The Different Frequency of Sound Field Sound Identification Under Phase Diagram

实验2让声源以相同的速度运动，通过LMS系统获取实验数据实现声源识别，最终得到的识别效果，如图8所示。

图8 LMS测试系统识别下的不同频率声场图Fig.8 The Different Frequency of Sound Field Map Recognition Based on LMS Test System

实验3首先通过LMS系统获取实验数据，利用离散余弦变换以采样率0.2对收集到的原始图像和语音信号进行稀疏化处理，再以高斯随机矩阵作为测量矩阵得到原始信号的测量值，然后通过ROMP重构算法得到处理后的信号。最后通过模拟软件对压缩重构的信号进行分析，实现到声源识别，经过处理后得到的效果图，如图9所示。

5.2 识别效果分析

以上数据是不同频率的声源在运动过程中随机选取的一点，并用三种不同的方式对声源识别研究得到的结果。下面分别以偏移距离、区域面积以及测量声压级范围来判断声源识别效果的优劣，其中偏移距离表示的是识别的声源所在位置与麦克风阵列中心点位置的偏移量，数值越小说明声源点越接近理想的中心位置。区域面积是对声源识别性能的判断，首先可以判断是否存在虚假声源，因为本实验在消声室进行，可以不考虑虚假声源。其次在偏移距离一定的情况下，区域面积越大说明对声场的描述越详细即识别的效果越好。下面分别对500Hz、1kHz以及3kHz声源的整个运动过程选取具有一定代表性的点做分析，结果，如图10、图11所示。

图10 不同频率下的偏移距离图Fig.10 The Offset Distance Map Under Different Frequency

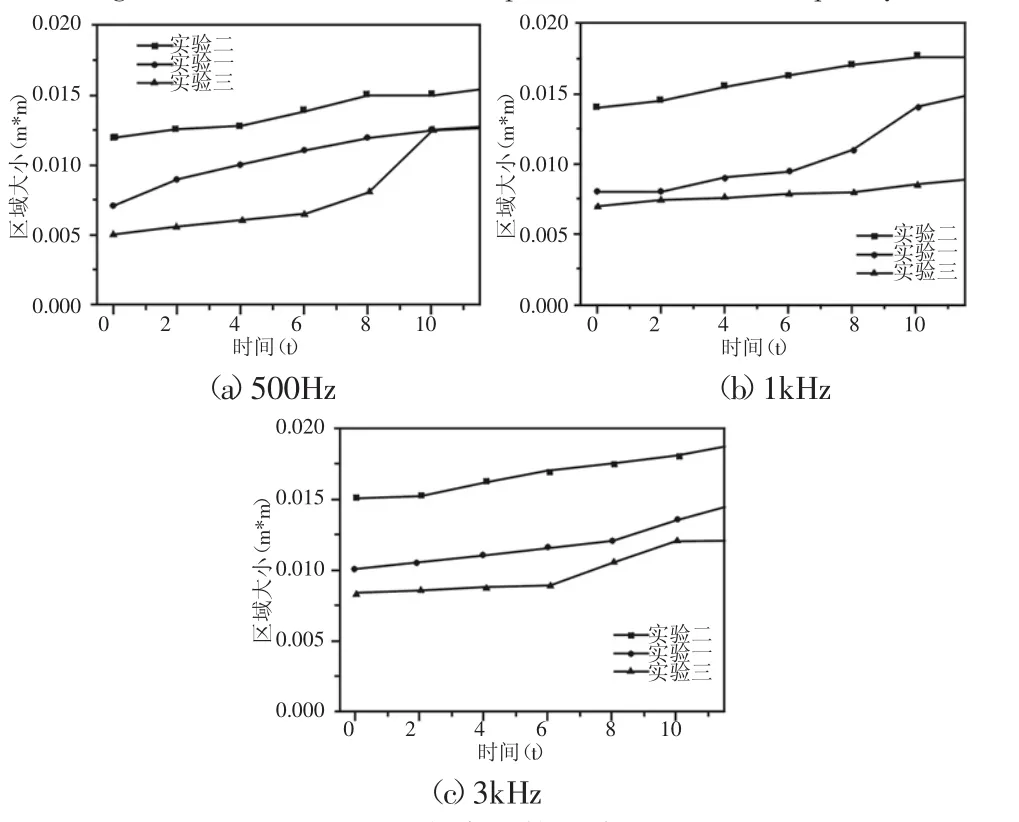
图11 不同频率下的区域面积图Fig.11 Regional Area Map at Different Frequencies

从以上数据分析得出：基于压缩感知理论实现的声源识别相对于其他两种实验方法而言，产生的偏移量较大，但是随着时间的变化，信号的收集趋于稳定，在第8s以后，偏移距离几乎不再变化，且从数据来看和其它两种方法几乎可以达到相同的偏移量。从区域面积的角度分析，面积也是随着时间在变化，并逐步趋于稳定。

6 结论

通过对常见的几种稀疏字典，测量矩阵以及重构算法的分析研究，得出了适用于运动运动声场的压缩和重建的最佳理论基础，即用离散傅里叶变换作为稀疏基矩阵，用高斯随机矩阵作为测量矩阵，用ROMP算法作为重构算法。通过三种不同的实验方法针对相同条件下的运动声源进行识别，实验结果表明经过稀疏重构以后的数据可以更加清晰的实现运动声源的识别，尤其是高频声源。为将来的高速、变速、多点声源的识别研究提供指导意义。

［1］Lustig Metal.Compressed sensing MRI［J］.IEEE Signal Processing Magazine，2008，25（2）：722-732.

［2］E.Candes.Compressive sampling Proceedings of the International Congress of Mathematicians［J］.Madrid，Spain，2006，3（2）：1434-1452.

［3］David L Donoho.Compressed Sensing［J］.IEEE Transactions on Information Theory，2006，52（4）：289-306.

［4］D.L.Donoho，Y.Tsaig，I.Drori，J-L.Starck.Sparse solution of under determined linear equations by stage-wise Orthogonal Matching Pursuit［J］.IEEE Trans.Inf.Theory，2012，58（2）：1094-1121.

［5］E.J.Candes，Y.Eldar，D.Needell，P.Randall.Compressed sensing with coherent andredundant dictionaries［J］.Applied and Computational Harmonic Analysis，2011，31（1）：59-73.

［6］F.Krahmer，R.Ward.New and improved Johnson-Linden embed-dings via the Restricted Isometrics Property［J］.SIAMJ.Math.Anal.，2011，43（3）：1269-1281.

［7］石光明，刘丹华，高大化.压缩感知理论及其研究进展［J］.电子学报，2009，37（5）：1070-1081.（Shi Guang-ming，Liu Dan-hua，Gao Da-hua.Compressive sensing theory and its research progress［J］.Electronic Journal，2009，37（5）：1070-1081.）

［8］李树涛，魏丹.压缩传感综述［J］.自动化学报，2009，35（11）：1369-1377.（Li Shu-tao，Wei-Dan.Summary of compressive sensing［J］.Journal of Automation，2009，35（11）：1369-1377.）

［9］刘志红，仪垂杰.旋转运动声辐射的解析方法［J］.机械设计与制造，2015，（12）：65-68.（Liu Zhi-hong，Yi Chui-Jie.The analytical method of mechanical design and manufacture of［J］.Machinery Design&Manufacture，2015（12）：65-68.）