1100铝合金双滚轮滚压包边模拟及实验研究
2018-03-21李萍井碧臣黄彪杨卫正薛克敏
李萍,井碧臣,黄彪,杨卫正,薛克敏
(1. 合肥工业大学 材料科学与工程学院,合肥 230009;2. 合肥工业大学 智能制造技术研究院,合肥 230009;3. 合肥工业大学 工业与装备技术研究院,合肥 230009)
包边是一种连接车身外板和内板的常见工艺,主要用在车门类总成,如车身四门两盖等,其优点主要体现在2个方面:一是滚压包边压合夹具可以根据产品的需要进行更换;二是可以根据需要,采用一模多机或是一机多模的工艺方案加工产品,因此研究机器人滚压包边技术有利于促进覆盖件在汽车上的使用。Livatyali[1—2]对包边工艺的流程进行了模拟,并在此基础上进行了优化实验,改良了翻边冲头和包边工具的结构,从而提升了包边质量。EDAG公司设计了滚压包边工具并申请了相关专利[3]。ABB公司研发了压力可控的滚压包边工具,通过实时控制滚轮施加在板件上的作用力提高滚压包边质量[4]。胡星等人结合实验和有限元仿真,研究了滚压包边过程中破裂极限准则[5]。JEE公司研发了机器人弹性滚压包边工具,成功完成了某商用车门盖的滚压包边[6]。N. Le Maout等[7]使用有限元分析方法研究了包边成形的过程,讨论了包辛格效应、材料各向异性等对包边结果的影响。Hu[8]等根据实验研究了铝合金材料的滚边断裂极限,结果表明,用Cockcroft & Latham塑性断裂准则预测滚边板料成形性能是有效的。李淑慧[9]等分析了铝合金滚边过程中循环硬化现象,结果表明在包边前材料的弯曲区域已发生了加工硬化,但在翻边区域材料的塑性变形很小。杨竹君[10]研究了单滚轮滚压包边工艺参数对滚压包边成形质量的影响。卢鹏[11]通过模拟及实验,研究了滚压包边工艺参数对铝合金材料成形质量的影响。国内外学者对滚压包边的研究都集中在单滚轮的包边过程,但对采用双滚轮同时进行板材滚压的研究较少。双滚轮相对于传统滚压包边的优点主要是柔性大,对外轮廓形状复杂的板材也能顺利地进行滚压包边加工,可以节约大量的生产成本,并大大缩短产品研制周期。文中针对汽车用隔热件的主要材料1100铝合金进行研究,采用有限元模拟和实验相结合的方法,研究了双滚轮情况下,滚压包边参数(翻边高度、TCP-RTP距离、滚轮半径、圆角大小等)对铝合金滚压包边成形质量的影响。
1 双滚轮滚压包边模型的建立
1.1 双滚轮滚压包边模型
双滚轮滚压包边是用板料下方的滚轮来代替传统滚压包边工艺的下模具,只需要用夹具固定住板材,利用滚压包边机器手带动滚轮进行板材的包边成形,在模拟中对整体模型进行简化,仅模拟出滚轮对板材的作用,不考虑工装夹具的位置,因为夹具一般设置在非变形区,对滚压包边不会产生影响,且工装夹具的约束作用,在模型的接触设置中会以“glue”的方式来体现。外板厚度为1 mm,长度为50 mm,包边的内板厚度为1 mm,长度为50 mm,内外板间隙为2 mm,西华大学王丽娟[12]的研究表明,为了避免波浪起皱过大,滚轮半径不宜小于15 mm,因此本次模拟在此基础上选择半径为10, 15, 20, 25 mm的滚轮,使用Simufact软件进行研究,在模拟中x方向为沿板宽方向,y方向为垂直板面方向,z方向为板长即滚轮滚动方向,双滚轮模型见图1。
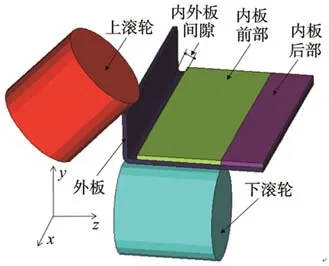
图1 双滚轮滚压包边模型Fig.1 Double-roller rolling hemming model
1.2 双滚轮模拟材料参数及边界条件
在本次模拟中,上、下滚轮及内板设置为刚体,外板板材的材质为1100铝合金,1100铝合金的弹性模量为69 GPa,泊松比为0.33,密度为2710 kg/m3,屈服应力≥100 MPa,抗拉强度为125 MPa。
使用Simufact软件自带的材料库中的“aluminum 1100(20 ℃)”即常温下的1100铝合金材料进行模拟。设置网格为六面体网格,网格大小为 0.2 mm×0.625 mm×0.625 mm,在变形量最大、最容易出现成形缺陷的外板折弯处采用局部网格细化,其网格大小为 0.1 mm×0.3 mm×0.3 mm,网格总数量为285 60个,各个部位网格密度见图 2。摩擦因数统一设置为 0.2。本次模拟采用二道次滚压包边,即第一道次由翻边后的90°板材滚压成 45°,二道次从45°滚压至 0°的成形方式进行滚压包边模拟。
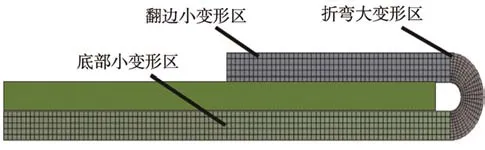
图2 各变形区及对应网格密度Fig.2 Each deformation zone and corresponding mesh density
在模拟中内板与外板采用“glue”接触,上、下滚轮与外板采用“touch”接触,内板固定不动,内板后部的下边缘(见图1)与外板上边缘glue接触,内板前部下边缘与外板上边缘“touch”接触。模拟开始时,滚轮先以45°压入外板,达到TCP-RTP值时,上下滚轮同时开始绕滚轮轴心旋转,并沿着板材轮廓向前进给,完成第一道次90°~45°包边;然后上滚轮旋转45°与下滚轮平行,再向下压入,直至外板与内板贴合,此时上下滚轮再同时旋转沿一道次进给方向返回至起点,完成二道次45°~0°包边。
1.3 模型的验证
取一组参数进行模拟并用同样的参数进行实验,分别在滚压完成后的板材上每隔5 mm取点,共取10个点,分别测量每个点的波浪起皱量及伸缩量,并分别将波浪起皱的实验值和模拟值作为横、纵坐标,拟合出如图3a所示曲线;同理绘制出图3b所示伸缩量的拟合曲线。对波浪起皱量,其r=0.984 58,最大误差为8.75%;对伸缩量,其r=0.989 91,最大误差为9.15%,证明了此有限元仿真模型的可靠性。
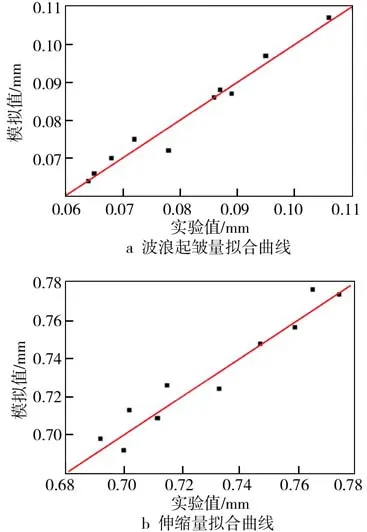
图3 实验与模拟的拟合曲线Fig.3 Fitting curve of experiment and simulation
2 双滚轮的模拟设计及数据处理
2.1 模拟及数据收集
在设置仿真模拟过程中,主要研究滚压包边参数对滚压包边后板件的波浪起伏和板件的伸缩量。根据华南理工大学卢鹏的研究[13],对传统单滚轮滚压包边影响最重要的参数分别为翻边高度、TCP-RTP、滚轮半径、圆角半径及滚压速度等,因此本次模拟选取上述5个因素并分别选取4个代表性的值,构成一个五因素四水平的 L16(45)正交模拟试验,利用 Simufact软件进行了16组仿真,分别计算出每一组的波浪起皱量以及伸缩量的数值,具体结果见表1。其中,波浪起皱量表征了滚压完成后的板材表面的平整程度,伸缩量表征了滚压完成后板材缩进或胀出程度。波浪起皱量及伸缩量的测量方法见图4。

图4 波浪起皱量及伸缩量的测量示意Fig.4 Measurement of corrugation amount and expansion amount of wave
在翻边的边缘均匀地取n个点,测量这个点距离内板上边缘的距离H,则波浪起皱量S计算见式(1)。用S的值描述整个翻边的波浪起皱程度,S越小表示板件越平整。

伸缩量的计算原理与波浪起皱量一样,只是测量的值L为滚压包边完成的板件折弯区外边缘最大轮廓到内板的距离,其计算见式(2)。

用T值描述整个翻边的缩进胀出程度,T越小表示板件越伸缩量越小,成形质量越好,本次模拟的模型长度为50 mm,因此每隔1 mm取一个测量点,共取50个点,进行数据统计,结果见表1。
2.2 数据处理及结果讨论
计算第 1列一水平对应的波浪起皱量数据的均值,填入表2均值1第1列位置,计算第1列水平二的波浪起皱量数据均值,填入表2均值2第1列位置,均值3和均值4的第1列数据同理可得;计算第2列一水平对应波浪起皱量数据均值,填入表2均值1第2列,以后的同理计算填入,以此得出表2如下。
根据表2中各均值,分别按列把每一列的最大值与最小值相减,得出每一列的极差,亦即每一种因素不同水平下其波浪起皱量的差别,此极差值越小,表明此因素对波浪起皱量影响越小。上述5种因素对波浪起皱量的影响为:翻边高度>TCP-RTP值>滚轮半径>圆角半径>滚压速度。由表2绘制每种因素对波浪起皱量影响的效应图,见图 5a。如滚轮半径在10~25 mm之间时,波浪起皱量随滚轮半径增大而增大,当滚轮半径为15 mm时达到最大,随后开始减小。其他几种因素的影响不再赘述。

表1 正交试验仿真数据及结果Tab.1 Data and results of orthogonal test simulation

表2 各因素、水平对应波浪起皱量影响均值Tab.2 Influences of factors and levels on the mean of corrugation amount of wave
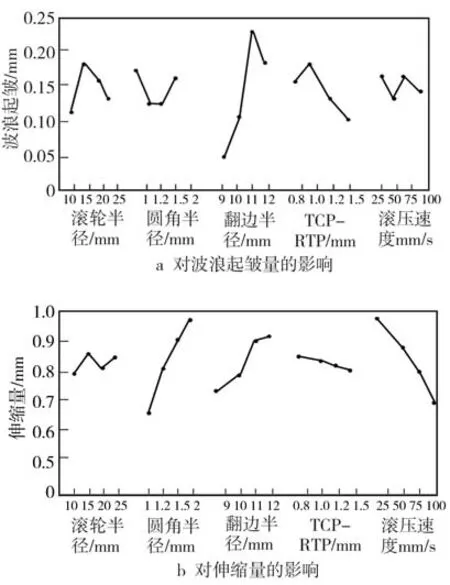
图5 各因素对滚压包边缺陷的影响Fig.5 Effect of each factor on defect of rolling Hemming
以同样的方法得出各因素、水平对应伸缩量均值及极差见表3,由表3可以看出,圆角半径因素的极差最大,达到了0.315,极差最小的因素为TCP-RTP值,其极差为 0.056。几种因素对伸缩量的影响程度为:圆角半径>滚压速度>翻边高度>滚轮半径>TCP-RTP值,并由表 3可以得出各因素对伸缩量的影响,见图5b。
由图5可以看出,当滚轮半径从10 mm向15 mm增大时,波浪起皱量和伸缩量均增大,从15~20 mm时波浪起皱量与伸缩量均减小,但当滚轮半径由20~25 mm时,伸缩量会变大,因此滚轮半径为20 mm的滚轮可以兼顾波浪起皱量及伸缩量;随着圆角半径增大,伸缩量呈上升趋势,因此圆角半径不宜过大,同时波浪起皱量在圆角半径为1~1.2 mm迅速降低,在1.2~1.5 mm时继续缓慢降低,因此综合考虑选取圆角半径为1.2 mm;由图5a及5b可以看出,翻边高度应该选用较小的值,但翻边高度过小会导致大变形区占比过大,影响实验结果,因此选取翻边高度为10 mm;随着 TCP-RTP值增大,波浪起皱量及伸缩量均呈现减小趋势,因此在TCP-RTP选择最大值1.5 mm;滚压速度对波浪起皱量影响较小,而对伸缩量影响较大,随着滚压速度增加,在25~100 mm/s范围内伸缩量减小,因此100 mm/s的滚压速度最优。
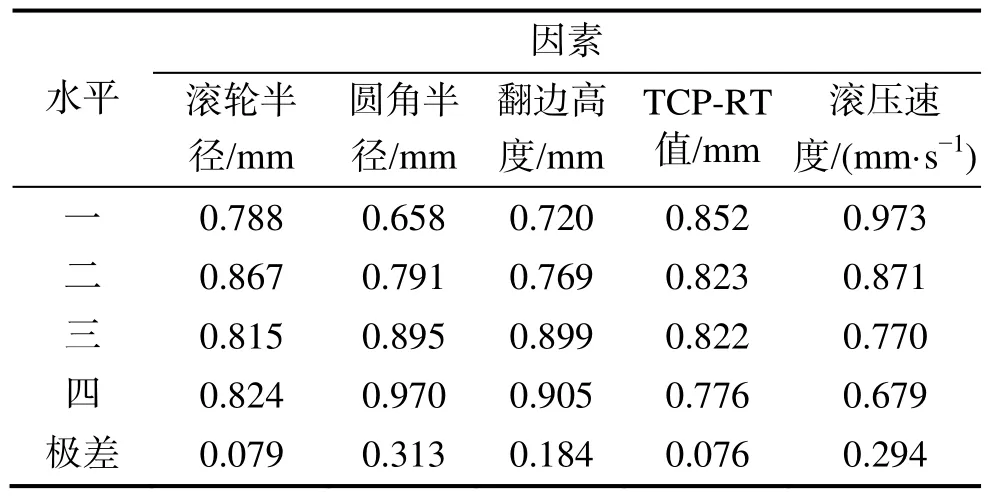
表3 各因素、水平对应伸缩量均值Tab.3 Mean value of expansion amount under all factors and levels

图6 滚压包边应力Fig.6 Stress in rolling hemming
2.3 缺陷形成机理及演化规律
滚轮由右向左滚压,将其经过的区域分为3个,A点所在区域为滚轮滚压完成且不受滚轮现在位置影响的区域(a区),B点区域为滚轮刚滚压经过的区域(b区),C点位于滚轮正在滚压的区域(c区),见图6a,图6a中左下角为方框部分的局部放大,右下角为左下角对应的背面区域。A点在x方向上受到b区及a区其周围点对其的压力,y方向上受b区变形时对其的压力,z方向上受b区对其的拉力;C点主要受滚轮对其的y方向的压力,x方向受到c区的拉力,而z方向受到b区及左边未变形区的拉力;B点在x方向受到来自c区的拉力,z方向受到a区和c区对其的压力。在a, b, c区均变形后,其板材纤维均被拉长,板材在z方向上相互挤压,而a及c区对b区的挤压以及b区下方板材对上表面板材的挤压导致b区的突起,形成褶皱,也就是宏观上的波浪起皱。滚压过程中a, b, c区不同时刻(图6b中20%为滚压包边进行20%时的应力曲线,下同)z方向的应力分布情况见图6b,可以看出,滚轮在滚边工艺进行40%后逐渐滚离b区,b区应力由此开始迅速增大,结合图6a可以得出,在此模型中,当板材z方向上受力大于30 MPa后,板材会呈现起皱状态。A、B、C三点的应力状态见图6c。
滚压包边过程中x方向的受力情况见图 6d,虚线下方为滚压完成后板材的伸缩缺陷,右下为方框区域放大图。滚压包边过程中不同时刻伸缩区的应力分布情况见图6e,可以看出,当滚压包边工艺进行20%以后产生伸缩缺陷的区域在x方向上受到的压力迅速增大,板材在x方向上的压力引起x方向板材纤维的伸长,这种延展导致了板料滚压以后产生伸缩缺陷。结合图6d可以得出,当x方向压应力大于20 MPa后,板材会出现明显的伸缩缺陷。
3 实验与模拟结果对比分析
3.1 最优数据组的模拟
以2.2中选取的最优参数组进行双滚轮滚压包边成形模拟及实验,实验中滚轮半径为20 mm,圆角半径为1.2 mm,翻边高度为10 mm,TCP-RTP值为1.5 mm,滚压速度为100 mm/s。模拟采用Simufact软件进行,其模拟过程及结果见图7。

图7 最优参数模拟过程Fig.7 Simulation process of optimal parameters
根据模拟结果采用取点方法测算出其波浪起皱量为0.046 mm,伸缩量为0.527 mm,此结果优于正交试验中绝大部分组别的结果。
3.2 双滚轮实验
实验采用 3自由度滚压包边机器人进行双滚轮滚压包边实验,上滚轮先保持45°压入,当上滚轮压入到设定TCP-RTP值即1.5 mm时,上下滚轮同时向前滚压,完成第一道次 90°~45°滚压;然后上滚轮旋转45°,水平压入板材,当压入到2个外板加1个内板距离后,上下滚轮同时向前滚动,第二道次即45°~0°滚压,完成双滚轮滚压包边过程。实验所用滚轮及1100铝合金板材及实验过程见图8。

图8 实验器材及滚压过程Fig.8 Experimental equipment and rolling process
在双滚轮滚压包边实验完成后,采用模拟中采用的取点测量方法,在图8的板材中同样取50个点,分别测量出每个点的波浪起皱量及伸缩量,最终得出此组实验的波浪起皱量为0.042 mm,伸缩量为0.498 mm。由此可得出实验与模拟的波浪起皱系数相差8.69%,伸缩量相差 5.82%,因此可以认为实验与模拟结果相当吻合。实验结果的波浪起皱系数即波浪起皱量相对于板厚(1 mm)的比例为4.20%,伸缩系数即伸缩量相对于板宽(10 mm)比例为 4.98%,明显小于一般铝合金滚压包边8%~12%左右的成形缺陷[13],证明了此双滚轮模具的合理性及工艺的可行性,且具有实际的生产意义。
4 结论
1)通过正交试验模拟及数据处理,得出双滚轮滚压包边模型各关键参数对波浪起皱量及伸缩量的影响。对波浪起皱量大小影响程度为:翻边高度>TCP-RTP值>滚轮半径>圆角半径>滚压速度;对伸缩量大小影响程度为:圆角半径>滚压速度>翻边高度>滚轮半径>TCP-RTP值。
2)波浪起皱的形成机理主要是前一个已变形区域(a区)及正在变形区(c区)对刚变形完成区域(b区)的挤压,导致板材纤维拉长引起的。对1100铝合金,当其z方向应力大于30 MPa后会产生起皱现象。伸缩量主要是由于滚轮滚压过程中滚轮对板材的压力导致板材纤维沿x方向拉长,当x方向压力达到20 MPa以后会出现显著的伸缩缺陷。
3)通过最优参数进行双滚轮的模拟与实验,分别得出实验结果与模拟结果的差值比率,波浪起皱量为8.69%,伸缩量为5.82%。波浪起皱系数为4.20%,伸缩系数为4.98%,证明了此双滚轮模具的合理性及工艺的可行性。
[1]LIVATYALI H, ALTAN T. Prediction and Elimination of Springback in Straight Flanging Using Computer Aided Design Methods: Part 1. Experimental Investigations[J]. Journal of Materials Processing Technology,2001, 117(1): 262—268.
[2]LIVATYALI H, LAXHUBER T, ALTAN T. Experimental Investigation of Forming Defects in Flat Surface-convex Edge Hemming[J]. Journal of Materials Processing Technology, 2004, 146(1): 20—27.
[3]QUELL E, HOHMANN M, BURZLAFF M. Roller Folding Head: U.S., 7152292[P]. 2006-12-26.
[4]PERSSON J. Tool for Automatic Roll Folding: U.S.,6640599[P]. 2003-11-04.
[5]HU Xing. Fracture Limit Prediction for Roller Hemming of Aluminum Alloy Sheet[J]. Materials and Design, 2010(32): 1410—1416.
[6]林巨广, 施成攀, 牛赵龙, 等. 机器人弹性滚边工具:
中国, 201011000730X[P]. 2011-04-13.
LIN Ju-guang, SHI Cheng-pan, NIU Zhao-long, et al.Robotic Roll-edge Tools: China, 201011000730X[P].2011-04-13.
[7]MAOÛT N L, MANACH P Y, THUILLIER S. Influence of Prestrain on the Numerical Simulation of the Roller Hemming Process[J]. Journal of Materials Processing Technology, 2012, 212(2): 450—457.
[8]HU X, LIN Z Q, LI S H, et al. Fracture Limit Prediction for Roller Hemming of Aluminum Alloy Sheet[J]. Materials & Design, 2010, 31(3): 1410—1416.
[9]LI S, HU X, ZHAO Y, et al. Cyclic Hardening Behavior of Roller Hemming in the Case of Aluminum Alloy Sheets[J]. Materials & Design, 2011, 32(4): 2308—2316.
[10]杨竹君. 机器人滚边工艺及系统研究[D]. 合肥: 合肥工业大学, 2012.YANG Zhu-jun. Study on Robot Roller Hemming Process and System[D]. Hefei: Hefei University Technology, 2012.
[11]卢鹏. 铝合金车身覆盖件滚边过程仿真及工艺参数优化[D]. 广州: 华南理工大学, 2015.LU Peng. Roller Hemming Simulation and Process Optimization about Panel of Aluminum Alloys Body[D].Guangzhou: South China University of Technology,2015.
[12]王丽娟. 机器人滚压包边成形缺陷的研究[D]. 成都:西华大学, 2013.WANG Li-juan. Research on the Forming Defects by Robotic Roller Hemming[D]. Chengdu: Xihua University,2013.
[13]卢鹏, 兰凤崇, 周云郊. 机器人铝合金滚边参数对其质量影响的研究[J]. 机械设计与制造, 2015(9): 101—103.LU Peng, LAN Feng-chong, ZHOU Yun-jiao. Research on the Influence of Rolling Parameters of Robot Aluminum Alloy on Its Quality[J]. Machinery Design and Manufacturing, 2015(9): 101—103.
