双金属复合管充液压形成形研究

林才渊，赵倩，初冠南

（哈尔滨工业大学（威海），山东 威海 264200）

双金属复合管可充分利用两种材料的性能，如铜/钢复合、钢/铝复合、铝/镁复合等，被广泛应用于航空、航天、电子等工业领域。目前，复合管的制备技术很多，其中大部分都是利用局部或整体塑性成形来进行复合的，能够制得双金属管材在非工作状态下呈紧密配合状态。根据现有研究情况可知，对于双金属复合管后续的加工成形研究还比较少，尤其是成形变截面中空管材类结构件。随着绿色制造和轻量化技术的发展，同时具有高强度和轻质量这类双层管结构件的需求量将日益增长[1—3]。

S. M. H. Seyedkashi[4]通过理论推导，得出了双层管液压内高压胀形破裂前的最大内压和避免起皱的最小内压的理论计算公式。孙显俊[5]等人利用有限元模拟，研究内压和摩擦对Fe/Al双金属复合三通管内高压胀形过程中减薄率的影响，并根据模拟进行了相应的试验。孔得红[6]等人采用气压胀形-冷缩结合工艺，获得正六边形截面 Mg/Al双金属复合异型管工艺。上述两种工艺均存在难以克服的缺点，如液压胀形所需成形压强大、成形极限小，气压胀形需要高温、成本大等。此外，Mohebbi[7]等人对旋压成形铜/铝复合管结构进行了理论模拟与试验验证，其工艺简单、成形效率高，但仍需要加热，因此，如何低成本、高效成形双金属复合管中空结构件迫在眉睫。为此，初等人[8—11]提出了充液压形方法，并将其应用在了高强钢和镁铝合金成形上。充液压形相较于传统气液胀形成形最大的优点在于其所需的内压更低，约为后者的5%～15%，所需合模力约为后者的50%，所需设备的吨位也大大减小。另外，由于在前者成形过程中，其内压很小，不会出现管材胀形，所以其壁厚均匀性更好。鉴于以上优点，文中采用充液压形技术成形Fe/Al双金属复合管，同时探讨其成形规律。

该技术在实际应用中由于是在弯矩作用下成形，极易发生回弹现象，进而导致内外管层间隙的出现，极大限制了后者的推广。考虑到内压是成形的关键参数之一，直接决定结果的成败，但前述研究均未探讨内压与成形件管层间隙的规律。此外，成形件壁厚均匀性也是决定该技术能否应用的标准之一。

1 充液压形技术思想

充液压形的技术原理见图1。首先，管坯通过预成形压成椭圆截面，并在内部施加一支撑内压，然后模具持续合模，在整个过程中，管坯在弯矩作用下逐渐贴模，见图 1a。模具合模一定程度后，管材与模具完全贴模，见图1b。

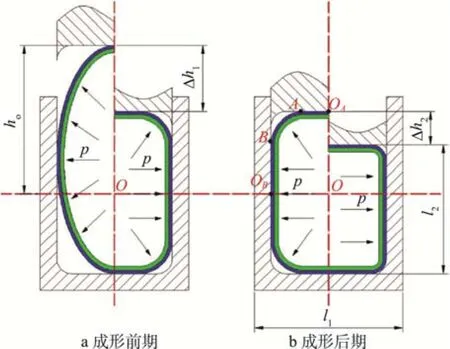
图1 充液压形原理Fig.1 Hydroforming principle

2 复合管成形数值模拟

2.1 研究方案制定

Fe/Al双金属复合管内层采用6063铝合金，外层采用DP600高强钢，两管材力学性能参数见表1。复合管初始管长50 mm，内层管壁厚为1.2 mm，直径为50 mm，外层管壁厚为1 mm，直径为54 mm，两者单边间隙2 mm。双层金属复合管液压成形过程分为内外层管胀接以及复合管成形2个阶段。内外层管胀接是指对内层管施加液压力，利用内外层管材料发生不同程度的变形，使外层管与内层管实现胀接，而为了保证双层管紧密结合，初始胀形内压需满足式(1)。同时，为了保证充液压形阶段管材直壁处不起皱的内压条件，见式(2)[12]，计算可得成形内压远大于胀形所需内压，进而保证初始胀形后内外管已经紧密贴合。根据上述实验思想，设计相应模拟方案。

式中：σs为准静态成形下的流动应力；t为管材壁厚；r为圆角半径；L为直壁长度；p1为管材胀形初始内压；p2为保证管材直壁不起皱最小内压。

表1 双金属复合管材料力学性能Tab.1 Mechanical properties of bimetal composite tubes

模拟模具所用形状见图1，l1=35 mm，l2=53.7 mm，圆角半径R=4.5 mm。Yang等研究了内压加载方式对铝合金成形性能的影响[13]，提出恒压加载成形壁厚分布最均匀，且该加载方式更适用于实际情况。故本研究设计了8组恒压条件下不同压力值加载曲线，见图2，同时考虑了内压为0时的加载条件。

图2 加载曲线Fig.2 Loading paths

2.2 模拟结果分析

不同压力下模拟得到的成形件回弹后结果见图3。内压为 0时，侧壁失稳起皱且内层管和外层管间隙很大。当内压为5 MPa及以上时，两管侧壁无起皱现象，但两者之间仍存有间隙，且随着内压的增大，间隙逐渐减小。经过测量，可以获得内外层管之间的间隙随着内压变化的精确值。不同成形内压回弹后双层管的形状及等效应力见图4。可见随着内压的增大，内外层管材的间隙逐渐变小。

由于胀形阶段，内压已经使内管与外管紧密贴合，因此间隙出现的直接原因为管材的回弹，且显然可见，内压大小决定着间隙的大小。根据充液压形的成形原理可知，弯矩是变形的驱动力，这是该技术和内高压成形的根本区别，因此成形中回弹是不可避免的。下面对这一成形规律进行详细分析。

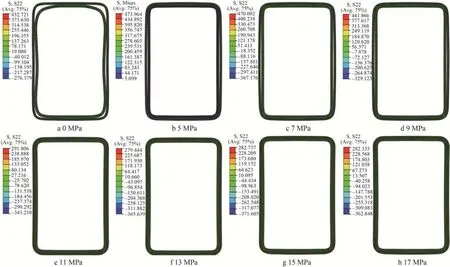
图3 不同内压下双层管回弹模拟结果Fig.3 Simulation results of double tube springback under different internal pressure

图4 回弹后管层间隙量Fig.4 Tube gap after springback

3 成形规律分析

为了能更好分析内外层管在不同内压条件下的回弹情况，提取模拟结果中两者的轮廓形状，并绘制成二维图，见图5，测量其回弹前后的尺寸，即可得回弹量。

考虑到结果中，两管直壁处间隙较大，故在本研究中仅选取直壁处的回弹进行力学分析。内压对回弹的影响见图6。外层管和内层管的回弹规律存在较大差异。

随着内压的增大，外层管的回弹方向发生了变化。当内压小于9 MPa时，回弹后的外层管宽度变大，且回弹量随着内压的增加，呈先增大后减小的趋势，当内压为 7 MPa时，回弹量达到最大；当内压大于9 MPa时，回弹后的外层管宽度减小，且回弹量随着内压的增加而增大，并逐渐趋向稳定。内层管的回弹方向未发生变化。其回弹量随着内压的增大，先减小后增大，当内压为5 MPa时，其回弹量达到最小值。结合内外层管回弹规律，可以看出两管之间的间隙主要由内外层之间的回弹量差值决定。随着内压的增大，复合管之间的间隙总体趋势逐渐减小。

图5 内外层管回弹二维Fig.5 Two dimensional drawing of inner and outer tube springback

图6 内压对回弹的影响Fig.6 Influence of internal pressure on springback

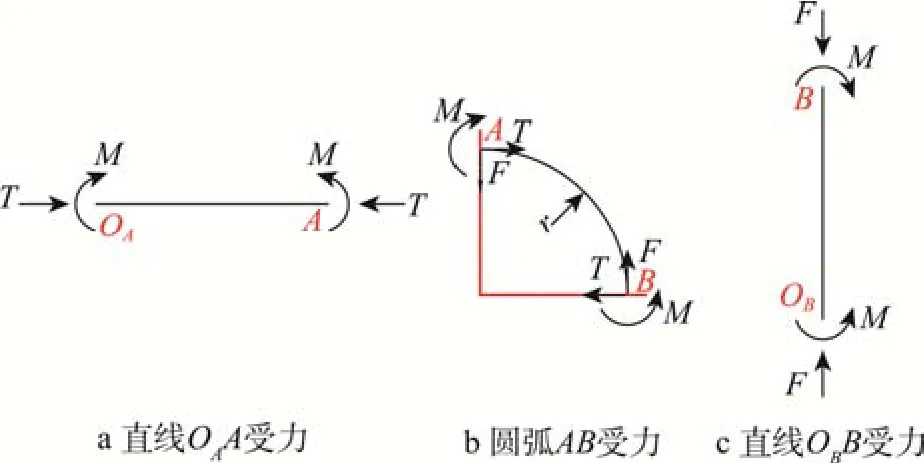
图7 受力分析Fig.7 Force analysis diagram

3.1 成形力学分析

取成形过程中的任意时刻进行分析，截面形状可认为是由已贴模的直线段和未贴模的圆角部分组成。相比于弯曲产生的应力，较小支撑内压所产生的摩擦应力可忽略，因此本研究忽略了摩擦的影响，并考虑到结构的对称性，取1/4进行受力分析。直线段OAA、OBB和圆弧AB的受力见图7，同时受压力和弯矩的作用。这是充液压形和气液胀形成形的根本区别。由于圆弧AB不是简单的几何形状，再加上成形过程中材料的非线性强化，力F、T和弯矩M难以给出解析解，因此本研究通过Abaqus有限元软件分析成形过程中内压对应力和弯矩的影响情况。所用单元类型为SR4，网格大小1 mm×1 mm。

通过图6发现，在7 MPa时，外管回弹量达到最大，在11 MPa时，外管的回弹方向发生改变，因此下面将通过模拟结果简要分析一下在这两个不同内压下，管材的受力情况及其对回弹的影响。考虑到回弹是由于弯矩导致的，而弯矩是通过管材环向应力沿横截面的分布积分所得，故需要分析后者在不同内压及压下量的具体情况。同时，为使结果对比明显，选取直壁处回弹量最大处横截面上的环向应力进行分析。

当内压为7 MPa时，内外管的直壁处环向应力各自的分布情况见图8。内压对环向应力分布影响见图6。对于p=7 MPa的条件，当压下量Δh为4 mm时，即上模位移量为4 mm时，外管直壁处外侧环向应力达到−250 MPa，而内侧环向应力达到363 MPa，两者应力差达到 613 MPa，而这也是弯矩产生的主要原因。出于计算方便的考虑，假设内外层管材应力分布呈线性分布，同时假设壁厚为1 mm，可得到此时弯矩大小为−53 N·mm。对于内层管直壁处，当上模位移量为4 mm时，其外侧环向应力达到24 MPa，而内侧环向应力达到4 MPa，两者应力差为20 MPa，求得弯矩为1.7 N·mm，相较于外管，内管的弯矩很小。当压下量达到 11 mm时，即成形结束，根据上述的计算方法，可以得到外管的弯矩大小为−50 N·mm，则其回弹方向为负，外管的弯矩大小为2.5 N·mm，回弹方向为正。根据上述计算，解释了当内压为 7 MPa时，内外层管的回弹方向相反。

图8 7 MPa内外管受力情况Fig.8 Force condition of 7 MPa tube inside and outside

同理，对p=11 MPa时进行理论分析，内外管受力情况见图9。当压下量Δh为4 mm时，外管直壁处弯矩大小为48 N·mm，内管直壁处弯矩大小为22 N·mm。当压下量Δh为11 mm时，外管弯矩大小为25 N·mm，内管弯矩大小为0.33 N·mm。同理，解释了当内压为11 MPa时，内外管的回弹方向相同。同时，内压为11 MPa时，内外管直壁处弯矩均小于当内压为7 MPa时，因而后续的回弹也相应的减小。

3.2 内压对壁厚分布的影响

壁厚均匀性也是对成形件的精度要求之一。外管DP600和内管6063成形后的壁厚分布以及整个复合管壁厚分布见图10，测量按照图10中箭头从下往上测量，即从A到B顺序。从图10b可知，由于压强大于内管6063的屈服压强，内管发生整体塑性胀形，根据体积不变原则，可以计算出胀形后内管壁厚为1.71 mm。同时可以发现，内压对内外管的壁厚分布影响还是非常有限的。不仅仅内外管的壁厚分布规律相似，复合管整体的壁厚分布规律同前两者也是相同的。这可见胀形后的6063内管和外管之间的接触非常紧密，变形同步性比较高。

图9 11 MPa内外管受力情况Fig.9 Force condition of 11 MPa tube inside and outside

在沿环向壁厚测量中，可见上下两个圆角处壁厚和直壁处壁厚分布差异较大，这主要是由于摩擦影响。模具的运动方式决定了在该实验中，摩擦力作用方向是与运动方向相反的，因而摩擦力对管材的作用力方向向下。故下圆角A处，等效应力较大，容易达到屈服状态，所以材料更容易屈服，材料更容易流动，这也就增加了壁厚的不均匀性，所以材料在下圆角处堆积明显。同时内外管的上下直壁处，壁厚减薄较为严重。其主要原因，由于需要将管材放于模具内，预成形压扁导致其在上下直壁位置处发生弯曲，从而是该处壁厚发生减薄。

从上述分析可见，内压对成形件的壁厚分布影响并不明显，同时成形件的壁厚均匀性也较为一致，相较于其他成形方式更适合于实际应用。

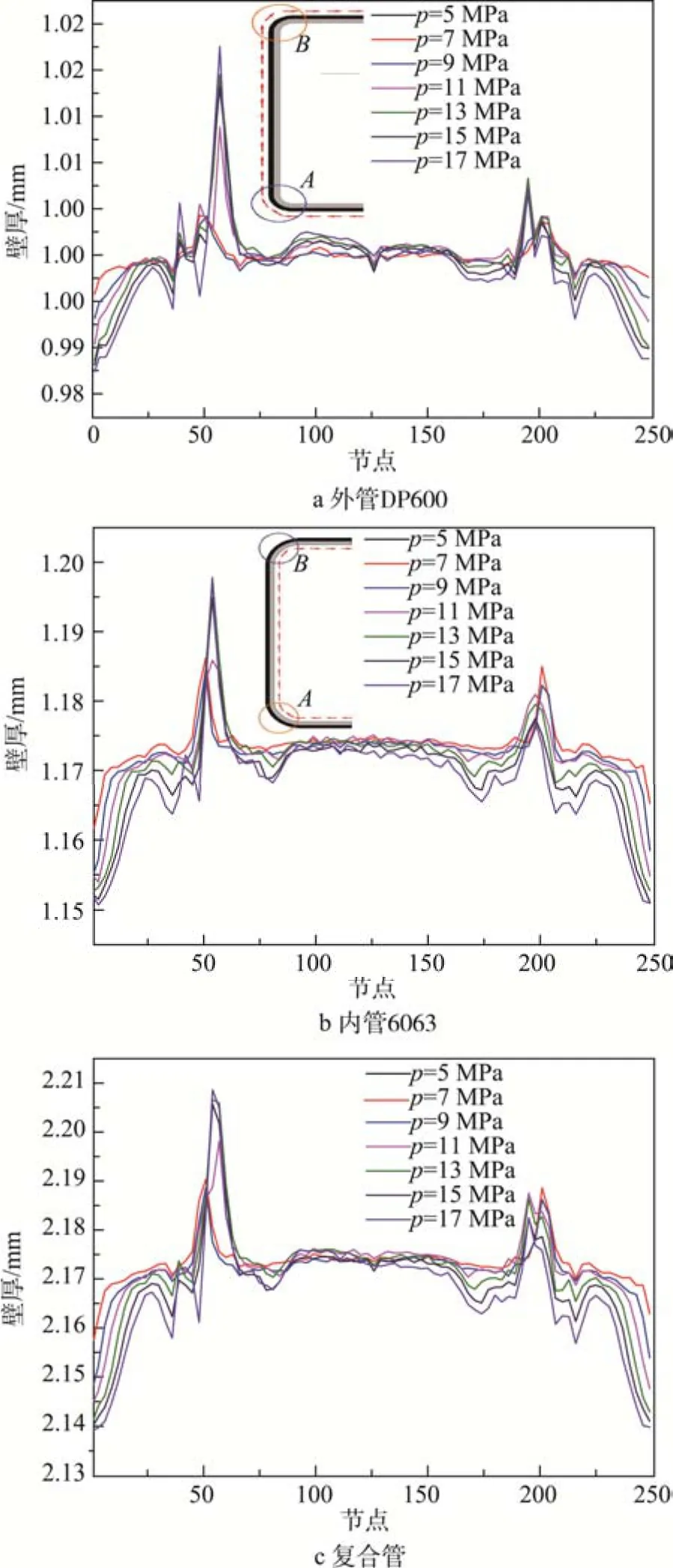
图10 复合管壁厚分布Fig.10 Wall thickness distribution of composite pipe

4 实验结果

根据模拟计算结果可知，实际成形过程中可以通过改变内压大小来控制Fe/Al双金属复合管的成形质量，内压力越大其成形效果越好。

同模拟制定方案相同，实验管材内管为6063铝合金，外管为 DP600高强钢，处于密封考虑，内管两端长度相较于外管长。为了将管材放入模具中，先将管材进行预处理，即将其压成椭圆，随后立即进行热处理退火，消除残余应力对后续实验的影响。不同内压下实验结果见图 11，随着内压的增大，内外层管之间的间隙逐渐减小，这与模拟结果的趋势是相一致的。

图11 不同内压下实验结果Fig.11 Experimental results under different internal pressure

5 结论

1)相较于气液胀形，充液压形由于弯曲作用力的引进，使其成形所需的内压更小，因而更适用于双金属复合管，且所需压力仅为17 MPa。

2)双层金属复合管充液压形的主要缺陷形式为回弹导致的内外层管接合不紧密。弯矩是导致回弹发生的主要原因，增大内压可减小间隙缺陷。在本研究中，当内压小于2 MPa时，容易因为内压过小而导致内外管发生弯曲起皱；而随着内压的增加，则可以很好地减小甚至消除内外管间隙。

3)对于Fe/Al双金属复合管而言，两者回弹形式存在较大差异。DP600外层管，随着内压的增大，回弹方向会发生变化，且回弹整体趋势随着内压的增大而趋于稳定值；6063内层管，随着内压的增大，其回弹方向不会发生改变，回弹量会随着内压的增大先减小后增大，并同外层管类似，回弹量趋于稳定值。虽然回弹是导致间隙存在的主要原因，但对于 Fe/Al双金属复合管材而言，内压的增加可以减小间隙，形状误差小于0.0316 mm，在实际生产实践中基本可以满足精度要求，可以忽略不计。

4)相较于内高压成形，充液压形成形双金属复合管还具有成形件壁厚分布均匀的优点。其壁厚相差最大仅为0.06 mm，已满足实际应用需求。

5)通过上述的实验与理论分析，基本掌握了Fe/Al双金属复合管充液压形的成形规律，并通过实验进一步地验证本规律的可行性。与传统双金属复合管成形方式相比，充液压形成形该类材料中空零件时，成形所需内压小，成形精度大，加工效率高，非常适合在实际生产中应用并推广，而这也是本研究中最为重要的成果之一。

[1]WANG M Z, ZHANG X R, FAN X J, et al. Study on Forming Process of Copper/Steel Bimetal Composite Pipe[J]. Mechanical Management & Development, 2012,3(127): 52—53.

[2]闫辰侃, 池成忠, 梁伟. 铝镁叠层板的热轧成形及热冲压成形性能研究[J]. 塑性工程学报, 2013, 20(5): 88—90.YAN Chen-kan, CHI Cheng-zhong, LIANG Wei. Research on Hot Rolling Forming and Hot Formability of Aluminum Clad Agnesium Sheets[J]. Journal of Plasticity Engineering, 2013, 20(5): 88—90.

[3]JIANG S, ZHANG Y, ZHAO Y, et al. Investigation of Interface Compatibility During Ball Spinning of Composite Tube of Copper and Aluminum[J]. International Journal of Advanced Manufacturing Technology, 2016,88(1): 683—690.

[4]SEYEDKASHI S M H, PANAHIZADEH V, XU H, et al.Process Analysis of Two-layered Tube Hydroforming with Analytical and Experimental Verification[J]. Journal of Mechanical Science and Technology, 2013, 27(1):169—175.

[5]孙显俊. Fe/Al复合管液压胀形数值模拟及试验研究[J].锻压技术, 2010, 35(3): 66—70.SUN Xian-jun. Fe Simulation and Practice of the Hydro-Bulging Process for Fe/Al Clad Tube T-Shape[J].Forging & Stamping Technology, 2010, 35(3): 66—70.

[6]孔得红. AZ31/7475双金属复合管气压胀形-冷缩结合工艺研究与力学分析[D]. 哈尔滨: 哈尔滨工业大学, 2017.KONG De-hong. Research on Gas Blow Forming-Cooling Contraction Bonding Process and Mechanics of AZ31/7475 Bimetallic[D]. Harbin: Harbin Institute of Technology, 2017.

[7]MOHEBBI M S, AKBARZADEH A. Fabrication of Copper/Aluminum Composite Tubes by Spin-bonding Process: Experiments and Modeling[J]. The International Journal of Advanced Manufacturing Technology, 2011,54(9): 1043—1055.

[8]李伟, 初冠南, 丁名区, 等. 带筋管整体成形力学条件研究[J]. 精密成形工程, 2016, 8(5): 76—80.LI Wei, CHU Guan-nan, DING Ming-qu, et al. Mechanical Conditions of Stiffened Tube during Hydro-assisted Forming[J]. Journal of Netshape Forming Engineering,2016, 8(5): 76—80.

[9]初冠南, 赵立栋, 魏玮, 等. AZ41镁合金管材充液压形规律探究[J]. 精密成形工程, 2016, 8(5): 71—75.CHU Guan-nan, ZHAO Li-dong, WEI Wei, et al. Hydrobulging Forming of AZ41 Magnesium Alloy Tube[J].Journal of Netshape Forming Engineering, 2016, 8(5): 71—75.

[10]初冠南, 张坤, 陈刚. 带筋管充液压形实验研究[J]. 精密成形工程, 2015, 8(1): 31—35.CHU Guan-nan, ZHANG Kun, CHEN Gang. Hydro-assisted Forming for Stiffened Tube with Ultra-ratio of Radius to Thickness[J]. Journal of Netshape Forming Engineering, 2015, 8(1): 31—35.

[11]李伟, 初冠南, 王红. 带筋管充液压形主要缺陷形式及控制方法[J]. 塑性工程学报, 2016, 23(6): 64—70.LI Wei, CHU Guan-nan, WANG Hong. Main Defects of Hydro-Assisted Press Forming of Stiffened Tube and Control Method[J]. Journal of Plasticity Engineering,2016, 23(6): 64—70.

[12]NIKHARE C, WEISS M, HODGSON P D. Buckling in Low Pressure Tube Hydroforming[J]. Journal of Manufacturing Processes, 2017, 28: 1—10.

[13]YANG Lian-fa, TAO Zhi-hua, HE Yu-lin. Prediction of Loading Path for Tube Hydroforming with Radial Crushing by Combining Genetic Algorithm and Bisection Method[J].Journal of Engineering Manufacture, 2015, 229(1): 110—121.