跳跃扩散Cox-Ingersoll-Ross利率模型

盛 洁，闫理坦

（东华大学 理学院，上海201620）

短期利率模型的成功性（体现在如Vasicek模型和Cox-Ingersoll-Ross模型等），主要在于模型在解析债券和债券期权定价上的可能性。经典的时齐利率的模型包括Vasicek（1977）、Dothan（1978）和Cox-Ingersoll-Ross（1985）模型。这些经典模型的表达式均为连续时间扩散随机微分方程，拥有如下形式

为了更加准确地描述利率数据变化的随机现象，随后带跳的扩散过程得到了发展，并被广泛应用于实时变化的股价、收益率、固定收益、能源等市场，及信用相关的固定时间序列，如贷款、企业债券等。现有大量证据表明金融过程中存在跳。早在1996年，Bates[1]就研究了货币市场中DM期权的跳过程；2002年Andresen[2]等人以及2003年Eraker[3]等人研究了股票市场的跳过程；Duffie和Singleton[4]研究了风险信用问题中的跳过程；2004 年，Johannes[5]、Piazzesi[6]研究了债券市场的跳过程；Barndorff-Nielsen 和 Shephard[7]、Chen[8]、Anderson[9]等人研究了收益的波动中的跳过程。从统计角度看，跳跃扩散过程是相对扩散过程的一个更一般的模型，更贴近真实情况，且对真实情况有更好的处理效果（White[10]研究结果显示带跳模型可以对真实的数据更好地近似）。而在经典的时齐短期利率模型中，Cox-Ingersoll-Ross模型在Vasicek的基础上在扩散系数中加入了平方根项，从而保证了它的瞬时短期利率始终为正，这与Vasicek模型相比更符合利率的实际情况。

因此，该文主要研究的是带跳的Cox-Ingersoll-Ross模型（以下简称为JCIR模型），以求更加贴近实际的利率数据情况。

1 跳跃CIR模型

在CIR模型中加入跳跃项，同时又保留对债券价格的分析可追踪性，Jamshidian附息国债和掉期期权分解部分可行性等其他的一些性质。假设

其中J是纯跳过程，跳跃发生率λ＞0，R+上跳跃尺度的分布为π。值得注意的是，限制了跳跃是正的，保留基本CIR过程的利率为正的特性。假设π是一个指数分布，期望为μ＞0，且其中M为强度为λ的时齐泊松过程，Ys呈参数为μ的指数分布。λ越大，发生跳跃频率越高，μ越大，跳跃的尺度越大。为了更直观的观察，（1）式还可以写成

其中W是标准布朗运动，Nt是泊松过程，跳的尺度J服从均值为μ的指数分布，跳发生时间服从均值为l=1/λ 的指数分布。 Wt和 Jt相互独立，跳跃尺度和跳跃发生时间相互独立。 则参数 θ=（k，γ，σ，μ，l）∈Θ⊆Rd，Θ是紧集。 借用 George[11]的结果，（2）式的转移密度特征函数（p=1，q=0）（给定 X0=x0，时间间隔为 δ）

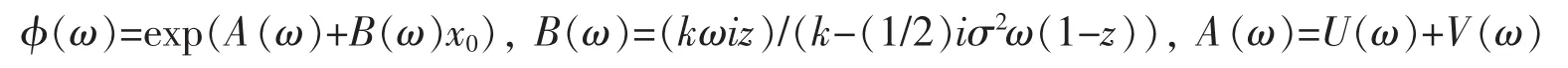
其中

2 Laplace逆变换

先来回顾一下逆变换的基本概念。设随机变量X为实值变量，有分布函数F，即F（t）=P（X≤t）。则X的特征函数（CF）为实数参数的复值函数

只需在特征函数上做一点小调整即可得到f的Fourier变换，也就是说，φ（-s）是f的标准Fourier变换，F的Fourier-Stieltjes变换。 若 f（t）定义在正实数上，则 φ（is）是 f的 Laplace变换、F 的 Laplace-Stieltjes变换。即对于密度函数的Laplace变换和Fourier变换可视为它的特征函数。事实上，无论是从理论上还是从实践上，Laplace逆变换效率更高，运算速度更快，也有更好的误差控制，与Fourier逆变换比唯一的不足是它只适用于正随机变量。然而CIR过程可以保证利率始终为正，因而文中选用Laplace逆变换。Laplace逆变换因其简单易操作的特性，而常被应用于各种领域，先从Laplace变换来看

若f（x）是非负连续随机变量X的概率密度函数，则X的特征函数为

因此，可由特征函数得f（x）的Laplace变换

由上述可见，若某非负连续随机变量的特征函数已知，即可通过Laplace逆变换求出它的概率密度函数。标准的Laplace逆变换为（7）式中Laplace变换函数的Bromwick等高线积分（选取特定的等高线并将其表达为实数域上取实值函数的积分）。任取等高线s=a使得没有奇异点，则

文中选取的Laplace逆变换的数值方法是Abate与Whitt[12]的欧拉法，它基于Dubner与Abate[13]和Simon与Stroot[14]的研究，使用Bromwick积分求各公式欧拉和。为了得到Laplace变换后的计算f（t）在点t的实数值。Abate与Whitt[12]给出数值算法

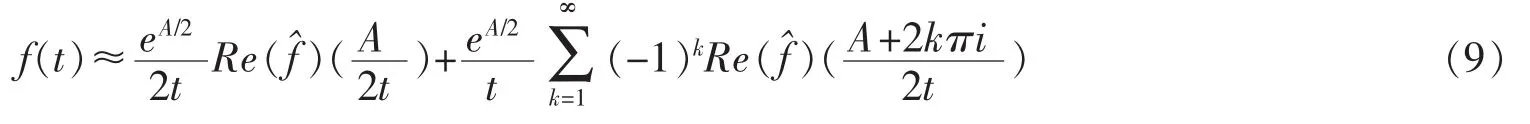
并用 E（m，n+1，t）-E（m，n，t）来估计误差。

3 贝叶斯估计的Monte Carlo模拟计算

由于大部分流行模型的似然函数都是未知的，短期利率模型的估计一直存在挑战。因而经常会选择使用近似的似然函数，但是这一操作会导致在估计的过程中产生偏差，所以文中使用似然函数的逼近的同时也使用了Monte Carlo方法来扩大数据量缓和离散和逼近带来的偏差。并且由Philip Gray[15]的研究结果显示，这种方法的贝叶斯估计后验密度的参数估计与真实后验密度极其相似。针对文中的目标短期利率模型，经验估计存在以下几个难题：（1）因JCIR的随机过程的转移密度是未知的，所以基于观察样本的似然函数的估计方法是存在问题的，而若是运用近似似然函数，则会在参数估计时引发偏差；（2）即便准确的似然函数已知，传统方法如极大似然估计一般采取大样本的结果来推导模型参数的联合分布，而这些渐进近似的有限样本表现主要还是未知的；（3）在数据采样频率（一般是按日、按周或按月）与连续时间假设的无限小时间间隔之间存在着显著差异，使用离散样本进行估计也可产生偏差。

在第二节中，已介绍了JCIR过程的转移密度特征函数，因而通过第三节的Laplace逆变换的数值方法得到转移密度函数的近似函数，如此算是初步解决了第一难题；估计参数的渐近正态性和渐近无偏性会在后续图表中有所显示；最后离散化所带来的偏差，文中将使用Markove Chain Monte Carlo（以下简称MCMC）法来对联合后验密度进行参数估计，同时运用Tanner和Wong[16]数据增强法则，在每对观察点间加入过程的模拟值点来使利率的观察样本得到扩大，从而减小离散化带来的偏差。对于JCIR过程在（4）式等距间隔h取样，并参考第四节中模型的第一种模拟方法，它的Euler离散近似为

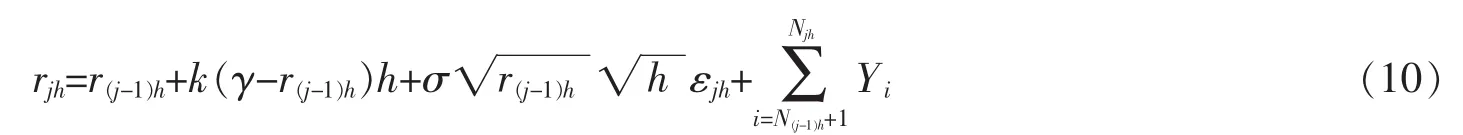
其中εjh～N（0，1）。近似似然函数则可由第二节中JCIR转移密度特征函数经第三节中的Laplace逆变换所得到的转移密度代替。

Euler近似的有效性来源于，当h趋于零时：（1）离散化的近似方程弱收敛于原随机微分方程；（2）Euler近似的似然函数收敛于原随机方程的似然函数，但是作为转移密度的近似误差太大，因为虽然近似中隐含假设随机过程在两观察点之间的路径为线性的，许多短期利率模型的路径却不是线性的。因此，Euler近似使用与观测值同样的频率来对过程进行离散是不合适的。为缓和偏差，根据Elerian、Chib和Shephard[17]的研究，通过增添一系列模拟点来增大观测数据。也就是为了减少离散带来的偏差，人为地制造一个频率足够高的样本来模拟JCIR路径：假设着手于一个在等距间隔h下有n个观测点的短期利率样本，用近似转移密度来模拟在每对数据观测点间的m个扩充数据，且仍假设扩充数据也是在等距间隔τ=h/（m+1），故这之后所有数据都可以按照间隔τ来查取。全体样本（观测值加上扩充值）总共由υ=nm+n个点组成，再加上初始值（假设r0是固定的）。令观测数据和扩充数据分别表示为robs和raug，观测数据点（扩充点）对应jτ/h，j=0，…，υ处的整数（非整数）值。想要估计模型参数（θ）以观测数据（robs）为条件的后验密度，基本上要将扩充数据（raug）看作未知参数。而模型参数和扩充数据的联合密度则由反复迭代条件密度 p（θ|raug，robs）和 p（raug｜θ，robs）得到。在一般条件下，这些条件密度的迭代收敛于真实联合分布 p（θ，raug｜robs），因此，目标后验密度 p（θ|robs）可由积分掉扩充数据后得到。

在τ划分的时间间隔下，（2）式的Euler近似如下

而假设 Yi服从正态分布 N（a，b2），则

又由M的独立性，有

根据贝叶斯法则，等价于

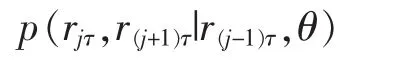
同样地，根据贝叶斯法则等价于

在 2003 年 Jones[19]提出了一种调整方式：先从 p（rjτ|r（j-1）τ，θ）生成可能在 r（j-1）τ之后的循环，接着仅留下（接受）在临近（r（j+1）τ之前的循环，且这个的接受概率由条件密度 p（r（j+1）τ|rjτ，θ）决定

鉴于（11）式的近似转移密度是正态（标准）的由上面（15）式生成的密度是平凡的。而Metropolis-Hasting算法则表明，每一次生成nm个扩展数据迭代点都可以简单的通过重复上述过程来遍历扩充数据组的每个元素。

结合上述的MCMC数值方法，目标联合后验密度的构造方法可以如下总结：

（1）从（12）式到（13）式，使用 p（θ[i]|raug，robs）迭代；

（2）在以 θ[i]为条件，参照（15）式的 Metropolis-Hastings 算法做迭代；

（3）以（16）式中给出的概率α为阀值来取（接受）迭代的

（4）然后重复上述过程直到得到一系列的（θ，raug）迭代。

在一般情况下，这个序列收敛于真实联合后验密度 p（θ，raug｜robs），而目标后验密度 p（θ｜robs）可将其中的扩充数据（raug）积分出去从而得到。

4 模拟结果

该节所展示的便是模型（2）在运用欧拉离散结果（11）式后得到的 θ≡（κ，γ，σ2，M）的贝叶斯估计，估计过程由上一节呈现。

表1显示的是模型参数的后验密度的均值与标准差。数据分类为30日、90日和180日银行承兑汇票（简写为BABs）以及13周和26周国债（简写为T-note），均来源于澳洲联储。BABs日度、周度和月度数据系列分别有6 512、1 526和307个观察样本，T-notes则为3 992、938和190个。参数的后验密度是由5 000个MCMC迭代和的m=2数据扩充估计来的。由表中数据比较可观察出，均值回归速度κ从0.09变化到0.16，BAB远期均值利率约在7%，比T-note略高（T-note约为4%）。波动率在不同BAB下浮动很大，在T-note下则较为一致。

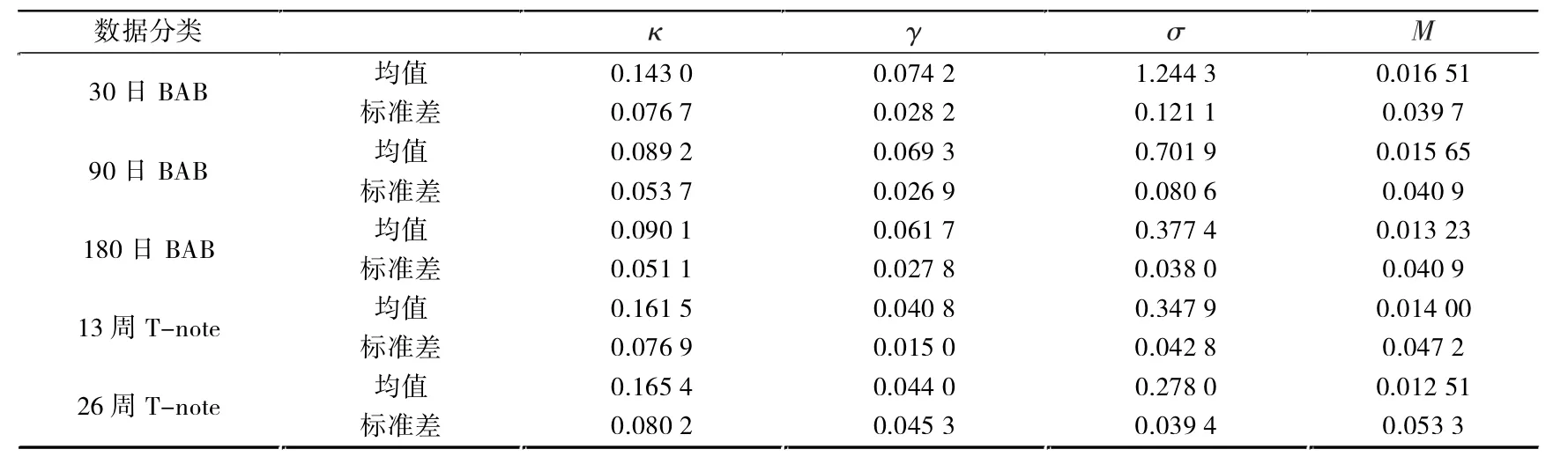
表1 不同数据分类下的参数估计

运用近似后验密度5 000次MCMC迭代法进行的点估计。近似密度由在每对观察数据之间模拟的的扩充数据点得到。BAB代表bank accepted bills，数据来源于澳洲联储1986年7月至2012年2月，总共1 526周度观察。T-note代表treasury note，由政府发放，数据从1996年6月开始直至2012年2月，总共938周度观察。

表2在与表1使用同样的数据来源下，比较了30日BAB数据分类时用不同的样本频率的估计结果。在不同频率的样本下参数估计十分稳定，唯一的例外是日度波动率，与表1中不同数据分类的波动率规律相比减小幅度较大。

表2 不同样本频率下的参数估计

运用近似后验密度5 000次MCMC迭代法进行的点估计。近似密度由在每对观察数据之间模拟的m=2的扩充数据点得到。数据来源于30日BAB的1 526周度观察，1986年7月至2012年2月。

[1]BATES D S.Jumps and stochastic volatility：Exchange rate processes implicit in deutsche mark options[J].Review of Financial Studies，1996，9：69-107.

[2]ANDERSON T G，BENZONI L，LUND J.An empirical investigation of continuous-time equity return models[J].The Journal of Finance，2002，57：1239-1284.

[3]ERAKER B，JOHANNES M，POLSON N.The impact of jumps in volatility and returns[J].The Journal of Finance，2003，58：1269-1300.

[4]DUFFIE D，SINGLETON K.Credit Risk[M].New Jersey：Princeton，2003.

[5]JOHANNES M.The statistical and economic role of jumps in continuous-time interest rate models[J].The Journal of Finance，2004，59：227-260.

[6]PIAZZESI M.Bond yields and the federal reserve[J].Journal of Political Economy，2005，113：311-344.

[7]BARNDORFF-NIELSEN O E，SHEPHARD N.Power and bipower variation with stochastic volatility and jumps[J].Journal of Financial Econometrics，2004，2：155-173.

[8]CHANG J，CHEN S X.On the approximate maximum likelihood estimation foar diffusion processes[J].The Annals of Statistics，2012，39：2820-2851.

[9]ANDERSON T G，BOLLERSLEV T，DIEBOLD F X.Roughing it up：Including jump components in the measurement，modeling，and forecasting of return volatility[J].The Review of Economic and Statistic，2007，89：701-720.

[10]WHITE H.Maximum likelihood estimation of misspecified models[J].Econometrica：Journal of the Econometric Society，1982，50（1）：1-25.

[11]DOTSIS G，PSYCHOYIOS D，SKIADOPOULOS G.An empirical comparison of continuous-time models of implied volatility indices[J].Journal of Banking and Finance，2007，31：3584-3603.

[12]ABATE J，WHITT W.Numerical inversion of laplace transforms of probability distributions[J].ORSA Journal on Computiong，1995，7：36.

[13]DUBNER H，ABATE J.Numerical inversion of laplace transforms by relating them to the finite fourier cosine transform[J].Journal of the ACM（JACM），1968，15：115-123.

[14]SIMON R，STROOT M，WEISS G.Numerical inversion of laplace transforms with application to percentage labeled experiments[J].Compute Biomed Res，1972，6：596-607.

[15]GRAY P.Bayesian estimation of short-rate models[J].Australian Journal of Management，2005，30：1-20.

[16]TANNER M A，WONG W H.The calculation of posterior distributions by data augmentation[J].Journal of the American Statistical Association，1987，82：528-549.

[17]ELERIAN O，CHIB S，SHEPHARD N.Likelihood inference for discretely observes nonlinear diffusions[J].Econometrica，2001，69：959-993.

[18]ERAKER B.MCMC analysis of diffusion models with application to finance[J].Journal of Business and Economic Statistics，2001，19：177-191.

[19]JONES C S.Nonlinear mean reversion in the short-term interest rate[J].Review of Financial Studies，2003，16：793-843.

[20]ZELLNER A.An Intriduction to Bayesian Inference in Econometrics[M].New York：John Wiley，1971.