微重力下低温贮箱内推进剂相变仿真模型研究

王 夕，王 珏，容 易，黄 辉



微重力下低温贮箱内推进剂相变仿真模型研究

王 夕1，王 珏2，容 易1，黄 辉1

（1. 北京宇航系统工程研究所，北京，100076；2.中国运载火箭技术研究院，北京，100076）

低温推进剂具有沸点低、易汽化的特点，相变是低温推进剂长时间在轨蒸发量控制问题中需要考虑的首要影响因素。相变模型对低温推进剂蒸发仿真起到重要作用，构建合理的相变模型成为低温流体蒸发量仿真重要的研究方向。基于4种相变理论，采用FLUENT软件二次开发的方法，建立基于相平衡和非平衡理论的4种相变模型，开展微重力下液氢推进剂蒸发的数值模拟，并与国外探空火箭试验进行比较和验证。研究结果表明：比较4种相变模型对贮箱内压力升高速率预示的准确性，得出了适用于微重力下低温推进剂仿真的相变模型。

低温推进剂；相变；微重力

0 引 言

在液体运载火箭的推进剂中，低温推进剂具有比冲高、沸点低、难于贮存的特点，因此限制了其长时间的在轨使用。对低温推进剂长时间在轨蒸发量控制问题的研究，可以采用试验和仿真的方法。鉴于低温和微重力试验的难度，基于已有商业软件的数值仿真是对贮箱内低温推进剂开展研究的有效途径。

目前，低温推进剂蒸发的数值研究受到广泛的关注。在低温推进剂蒸发量的所有影响因素中，相变是重要的考虑因素，相变过程的建模是蒸发量控制研究的焦点问题，而发展相变数值模型的基础是描述相变物理过程的理论模型。相变的理论模型包括相平衡模型和非平衡模型。相平衡模型中，假设液相和汽相之间达到平衡时，界面各相之间的温度相等，处于平衡状态[1]；而在非平衡模型中，Schrage[2]使用基于Maxwell速度分布来分析液/汽界面的传质过程，将界面的相变考虑为两相界面对液/汽分子的捕获和逃逸的非平衡过程；李震东[3]、Tanasawa[4]等总结了发生在液/汽相界面处的相变传质理论，归纳为相平衡模型和非平衡模型；刘秋生[5]等使用简化的Hertz-Knudsen方程对热毛细作用主导的流动进行了研究，对微重力下的相变问题具备参考价值。

基于以上两类相变理论，建立了相应的仿真模型，并用于低温贮箱推进剂蒸发的仿真中。其中，相平衡模型在低温贮箱CFD仿真中应用广泛。程向华[6]等根据相平衡建立了液氧贮箱的二维模型，分析了液氧热分层的形成过程及原因；Zilliac[7]等对贮箱进行建模，根据热力学平衡原理建立相变模型。相比于相平衡模型在低温推进剂相变仿真的广泛使用，非平衡模型的使用很少。Olga[8]等应用非平衡模型开展了液氢贮箱内径向喷雾的仿真，但并没有将非平衡模型与相平衡模型进行对比研究。

实际的相变物理过程在界面处存在温度跳变和非平衡的瞬态作用，与相平衡模型存在一定的差异，这些差异对低温推进剂蒸发数值模拟仿真准确性的影响仍未被讨论，比较不同相变仿真模型的准确性和适用性对低温流体仿真具有重要作用。

本文基于已有的相变理论展开了CFD建模工作，通过FLUENT用户自定义函数，建立基于不同相变理论的蒸发模型，并通过适当的假设修正蒸发模型，开展了贮箱内液氢蒸发仿真，与国外Areobee探空火箭试验[9]进行了对比，并分析了不同的相变模型在低温流体仿真中的应用。

1 数值模型

本文参照Aerobee探空火箭液氢蒸发试验[9]开展了数值模拟的对比研究，基于相平衡理论和3种非平衡理论，通过界面假设和蒸发假设，建立了仿真软件FLUENT下的相变模型，模拟试验贮箱内压力上升，验证并比较不同模型的结果，得到适用于微重力下低温推进剂蒸发量预示的数值仿真模型。

1.1 控制方程

采用二维轴对称模型，对液氢贮箱推进剂受热蒸发的过程进行分析。控制方程为连续方程、N-S方程和能量方程，对于每一相，有：

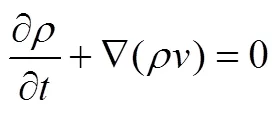
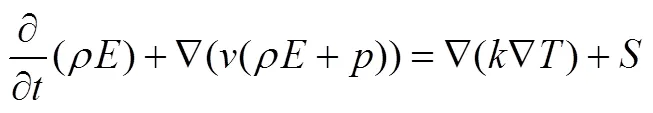
式中为密度；为速度；为动力粘度；为时间；为压力；为能量；为系统加速度；为温度；为体积力；为能量源项。

液相密度采用Boussinesq近似，其余物性作为温度的函数分段插值，气相则采用理想气体模型。

（4）

考虑到蒸发过程流速小，因此流动采用层流模型。

微重力下需要考虑表面张力作用，采用连续表面张力模型如下：

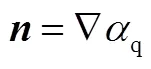
1.2 相变模型

相变模型是本文主要研究对象，基于两种假设，开展对4种相变模型的研究。

a）界面假设：相变仅发生在相界面处；

b）蒸发假设：只有在液相温度高于饱和温度时，才发生相变，不考虑冷凝的发生。

1.2.1 模型1

考虑使用相平衡模型[6]，液相的超过饱和温度的能量将全部转化为相变，模型1方程为

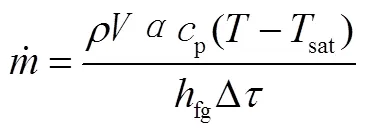
1.2.2 模型2

Schrage[2]推荐的非平衡模型，即Hertz-Knudsen方程为

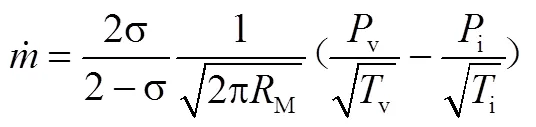
净质量流率为正值，表明气液界面上有净的质量从气相变为液相，即相界面上发生凝结；反之，如果净质量流率为负值，则相界面上将发生蒸发。

1.2.3 模型3

刘秋生[5]等提出采用非平衡热力学方法计算表面张力主导流动下的界面蒸发流量。蒸发界面假设为不变形，采用线性近似后的Hertz-Knudsen方程来描述蒸发界面的蒸发流量，即模型3：

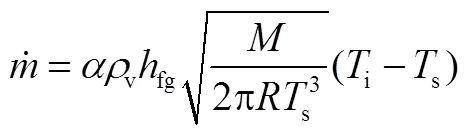
1.2.4 模型4

采用相变模型[4,10]，即模型4为

根据Tanasawa[4]的推荐值及实际计算的结果比较，取系数为0.2。

1.3 网格无关性验证

对采用的二维轴对称网格（见图1）开展网格无关性验证（见图2），使用相变模型1，比较3种不同网格数量，网格数分别为5000，10 000和20 000。

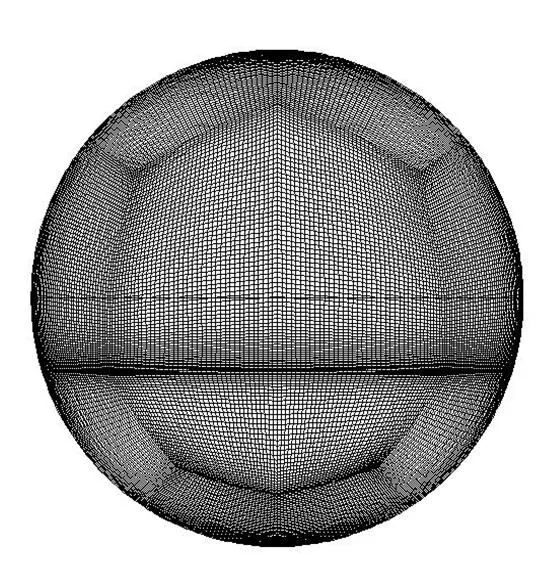
图1 采用的网格

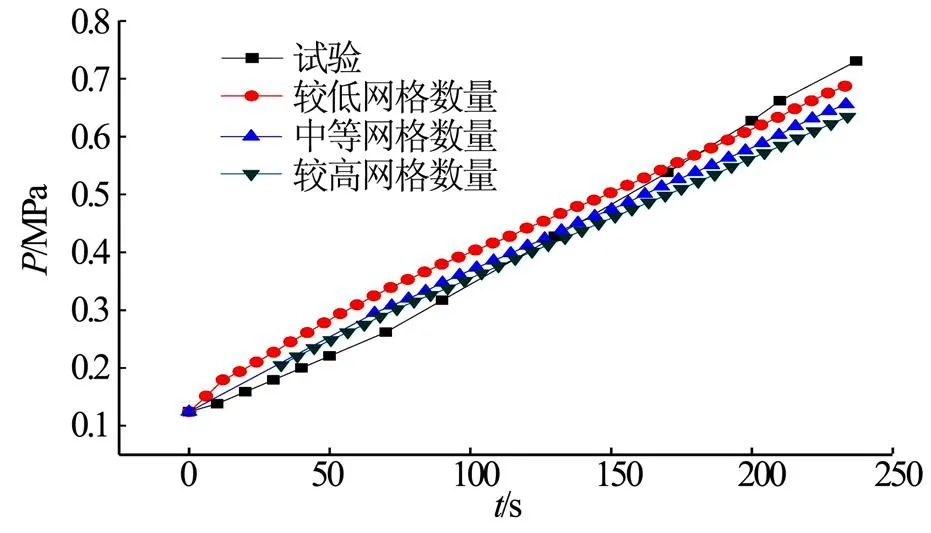
图2 网格无关性验证曲线

3种网格压力上升的偏差较小，其中与较高网格数量相比，中等网格数量的最终压力差值占总压力升高的4.17%，该偏差可以被忽略，结果较为一致。考虑到网格数的增加对计算效率的影响，采用中等网格数量开展数值仿真。

2 结果与分析

对4种相变模型开展研究，对比不同模型下贮箱内压力上升速率与试验实测值的偏差，同时对贮箱内的流体行为开展研究。仿真条件如表1所示，选取与试验相同的初始压力，并将初始温度设置为该压力下饱和温度。假设贮箱为均匀受热，选取试验中平均热流密度作为壁面热流边界条件。

表1 数值模拟条件

Tab.1 Conditions of Simulation

性能参数 球形贮罐直径/cm22.86 体积充填率34.3% 平均热流密度/（W·m-2）473.19 重力/（m·s-2）0.01 初始压力/MPa0.1241 总受热时间/s237

由于采用了两种假设，本文将对界面假设和蒸发假设的合理性展开讨论，并基于两种假设，对采用的4种相变模型的对比分析。

2.1 界面假设

界面假设将相变界定在界面处，是否采用界面假设将对结果产生影响。采用/不采用界面假设代表两种不同的相变原理。

汽化过程可分为界面蒸发和沸腾蒸发两种方式。当模型不采用界面假设，液相温度只要温度超过饱和温度，在任何位置均可发生汽化，这样的模型更接近于沸腾。然而，在实际过程中，液体内部发生沸腾并产生气泡需要达到一定的活化能，并非达到饱和温度即开始汽化，在较低热流密度的条件下相变往往以界面蒸发为主。热量传递到界面需要一定的时间，当界面蒸发主导相变时，不采用界面假设将高估汽化传质速率，即使与实际的沸腾过程相比，由于未考虑气泡生成的过热度，不采用加密假设的模型同样会高估汽化传质速率。

采用模型1和模型4来比较有/无界面假设的贮箱压力上升结果如表2所示。在237 s内，无界面假设的模型得到的贮箱压力和平均压力升高速率均高于试验值，而采用界面假设的模型得到的结果更接近于试验值。结果表明，不采用界面假设的模型将高估汽化传质速率，使压力快速升高；采用界面假设的模型更为合理，进一步支撑了假设的合理性。对照试验以界面蒸发过程为主，与沸腾过程有本质的区别，汽化过程仅发生在界面处，采用界面假设的模型也更符合实际。

表2 界面假设压力上升结果对比

Tab.2 Pressure Rise Result of Interface Assumption

模型终压/MPa压力升高速率/(Pa·s-1) 试验0.7302752557.7 模型1（无界面假设）0.8424493031.0 模型4（无界面假设）0.8882393224.2 模型1（界面假设）0.7569942670.4 模型4（界面假设）0.7682602718.0

在低温推进剂贮箱的相变仿真中，是否采用界面假设，取决于流体的形态。若贮箱受热较小，主要形态为界面蒸发，则使用界面假设；若贮箱受热较大，主要形态为沸腾过程，则应当考虑不采用界面假设。

2.2 蒸发假设

蒸发假设的实质是忽略冷凝的作用。在实际过程中，发生在气相内部（非界面处）的均匀冷凝一般很难发生，而非均匀冷凝则发生在有过冷界面存在的情形下[2]。而试验中不存在大过冷度的过冷界面，若认为只要低于饱和温度即发生冷凝，则可能高估冷凝的作用，造成计算偏差。因此，不采用纯蒸发假设可能高估冷凝的作用。

采用模型1和模型3来比较有/无蒸发假设的贮箱压力上升结果如图3所示。

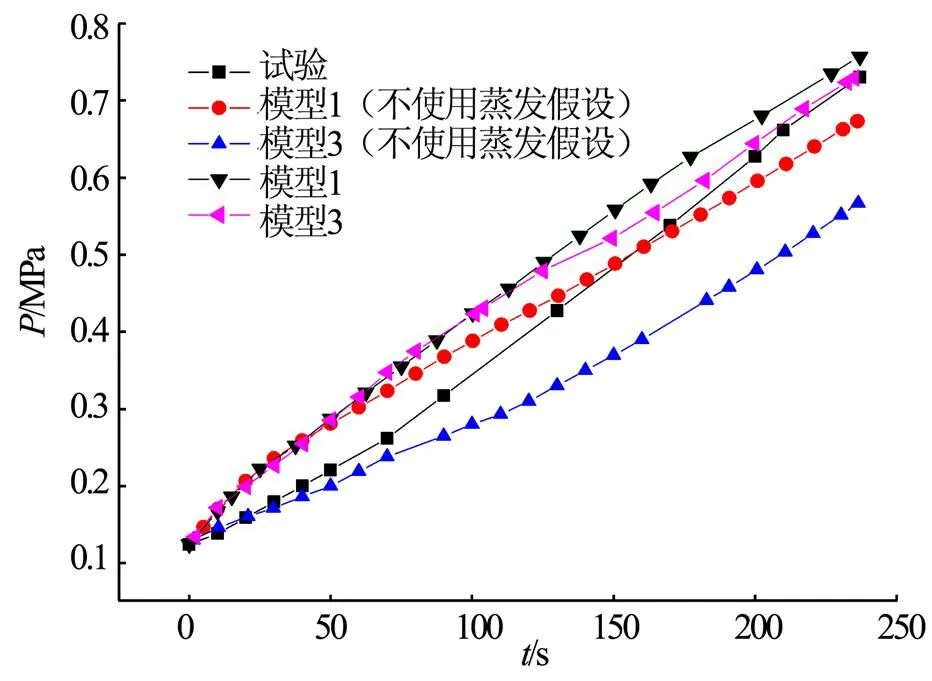
图3 蒸发假设压力上升结果对比曲线

图3中，最终的压力值和平均压力上升速率可用于比较分析。由于试验中加热器启动需要一定的时间，温度由开始加热到逐渐稳定，因此在试验初始阶段，加热的热流更小。而仿真中，热流边界条件设置为平均热流密度，并保持恒定值，因而图中曲线在100 s处压力比数值模拟结果低是合理的，最终压力是较为合理的比较参数。

由图3可知，不采用蒸发假设时，模型3的最终压力结果远低于试验值，而模型1的最终压力同样低于试验值。不采用纯蒸发假设的模型，高估了冷凝的作用，造成净汽化速率的降低，压力上升速率减缓，导致了与试验的偏离。

采用蒸发假设的模型1和模型3的最终压力值与试验值更接近，结果更准确。通过有/无蒸发假设的对比分析，在没有过冷壁面存在的条件下，采用蒸发假设的相变传质模型更合理。

2.3 4种相变模型的结果分析

在界面假设和蒸发假设下，对4种蒸发模型开展了对比研究，以分析模型的准确性以及相平衡模型和非平衡模型的差别。

4种模型结果对比如表3所示，4种模型的压力结果如图4所示。

表3 4种模型结果对比

Tab.3 Results of Four Models

模型最终压力/MPa平均压力升高速率/（Pa·s-1）偏差 试验0.730 2752557.7— 模型10.756 9942670.44.4% 模型20.657 5342250.8-12% 模型30.734 5462575.70.7% 模型40.768 2602718.06.3%

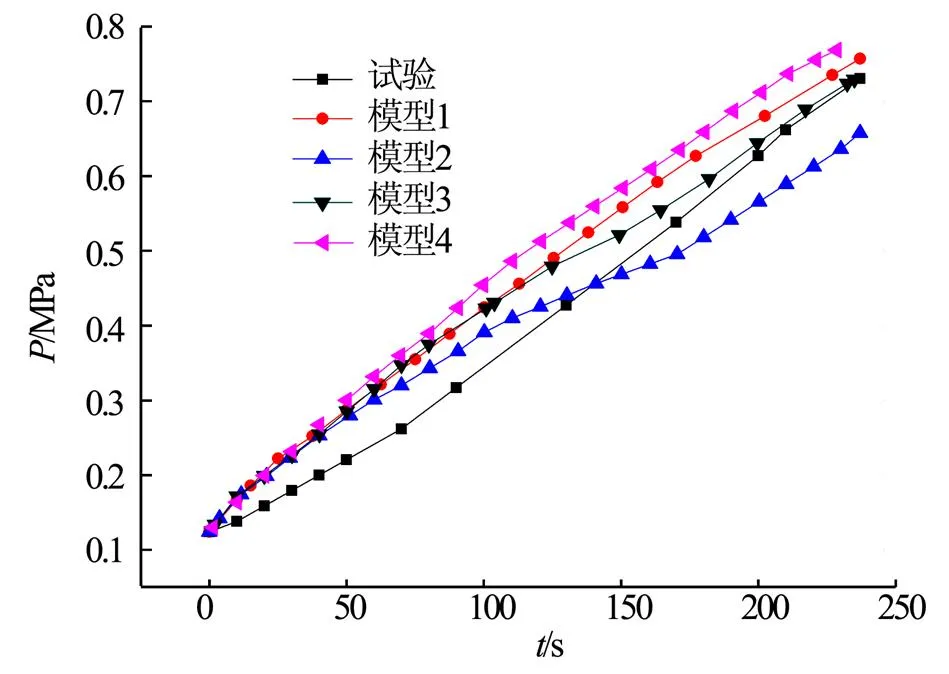
图4 4种模型压力结果

由表3可知，模型2的平均压力升高速率偏差最大，为-12.0%。由于在相变模型中考虑了压力，而压力是较为敏感的参数，同时考虑压力和温度也增加了模型的复杂性，其计算结果可能出现较大的偏差。

模型4的压力升高速率结果偏差为6.3%，比模型2的偏差更小，比其他两种模型略为偏大，略高于试验贮箱压力结果。模型1是相平衡模型，而其他3种模型均为非平衡模型。模型1的偏差为4.4%，结果优于模型2、模型4，略高于试验贮箱压力结果。

模型3的压力升高速率与试验的偏差最小，偏差为0.7%，最适合用于微重力下液氢贮箱蒸发量的预示。

通过4种模型的对比和分析发现，模型1、模型3及模型4的偏差均小于7%，对微重力下低温推进剂贮箱蒸发量预示的偏差均可被接受。其中，模型3考虑了在热毛细力主导下的界面蒸发，对微重力下的情形更为适用，其结果相比于其他3种模型具备明显的优势，偏差最小，适用于微重力下低温推进剂贮箱蒸发量预示和对贮箱压力升高的数值模拟，具备良好的准确性。

在国内外对低温推进剂蒸发的研究中，使用非平衡相变模型的较少，一般使用相平衡模型对蒸发过程进行数值模拟。根据以上的分析，相平衡模型具备在趋势上预测贮箱压力的能力，其仿真结果偏差在可接受的范围内，这些研究的结果并不会在趋势上受蒸发模型的影响。

在微重力这样的特殊环境中，模型3相比于相平衡模型和其他非平衡模型具备准确性优势。因此，在特定环境下，采用与环境相适应的非平衡模型将进一步提高仿真的准确性。

3 结 论

本文利用国外Aerobee探空火箭试验数据对微重力下液氢贮箱内相变仿真开展CFD建模工作，根据不同的相变理论，通过两种假设，对不同相变模型开展比较分析，得到如下结论：

a）在较低热流、贮箱内以界面蒸发为主导的情况下，宜采用界面假设；在没有过冷壁面存在的条件下，对低温推进剂受热蒸发相变的数值模拟宜采用蒸发假设。

b）本文比较了4种相变模型对封闭液氢贮箱内压力升高的预测，其中包括1种相平衡模型和3种非平衡模型，结果表明，模型1、3、4均能在趋势上对微重力下液氢封闭贮箱压力升高趋势进行预测，可有效模拟贮箱中的流体形态和温度分布。相平衡模型1具备对贮箱内压力升高趋势的预测能力。

c）非平衡模型3仿真结果更接近试验，对微重力下液氢蒸发的数值模拟具备良好的准确性，在微重力环境下的仿真中具备优势。在特定环境下，采用与环境相适应的非平衡模型将进一步提高仿真的准确性。

[1] 吴双应, 曾丹苓, 黄双, 等. 微层蒸发模型的非平衡热力学分析[J]. 热科学与技术, 2005, 4(4): 283-288.

Wu Shuangying, Zeng Danling, Huang Shuang, et al. Non-equilibrium thermodynamic analysis of micro-layer evaporation model[J]. Journal of Thermal Science and Technology, 2005, 4(4): 283-288.

[2] Schrage R W. A theoretical study of interphase mass transfer[M]. NewYork: Columbia University Press, 1953.

[3] 李震东, 赵建福, 鲁仰辉, 等. 池沸腾现象中热毛细对流的成因[J]. 空间科学学报, 2008, 28(1): 38-43.

LI Zhendong, Zhao Jianfu, Lu Yanghui, et al. Origin of thermocapillary convection in pool boiling[J]. Chinese Journal of Space Science, 2008, 28(1):38-43.

[4] Tanasawa I. Advances in condensation heat transfer[J]. Advances in Heat Transfer, 1991, 21: 55-139.

[5] 刘秋生, 汪洋, 纪岩. 蒸发相变与界面流动耦合机理研究[J]. 工程热物理学报, 2010(10): 1751-1754.

Liu Qiusheng, Wang Yang, Ji Yan. Coupling mechanism of evaporation phase-change and interfacial flow[J]. Journal of Engineering Thermophysics, 2010(10): 1751-1754.

[6] 程向华, 厉彦忠, 陈二锋, 等. 新型运载火箭射前预冷液氧贮箱热分层的数值研究[J]. 西安交通大学学报, 2008, 42(9): 1132-1136.

Cheng Xianghua, Li Yanzhong, Chen Erfeng, et al. Numerical investigation of thermal stratification in liquid Oxygen tank for new-style launch vehicle during ground precooling[J]. Journal of Xi'an Jiaotong University, 2008, 42(9): 1132-1136.

[7] Zilliac G, Karabeyoglu M A. Modeling of propellant tank pressurization[R]. AIAA, 2005-3549, 2005.

[8] Kartuzova O, Kassemi M, Agui J H, et al. A CFD model for the Multipurpose Hydrogen Test Bed (MHTB) ground-based self-pressurization and pressure control experiments[C]. Atlanta: 11th AIAA/ASME Joint Thermophysics and Heat Transfer Conference, 2014.

[9] Knoll R H, Smolak G R. Weightlessness experiments with liquid hydrogen in aerobee sounding rockets, uniform radiant heat addition-flight 1[R]. NASA TM X-484, 1962.

[10] ANSYS FLUENT 13.0 Theory Guide[M]. Canonsburg, PA, ANSYS. Inc., 2011.

Computational Research on Phase Change Model forCryogenic Propellant in Microgravity

Wang Xi1, Wang Jue2, Rong Yi1, Huang Hui1

(1. Beijing Institute of Astronautical Systems Engineering, Beijing, 100076; 2. China Academy of Launch Vehicle Technology, Beijing, 100076)

Boil off is a characteristic of cryogenic propellant, and the phenomenen of phase change is the major factor of cryogenic propellant storage on orbit. As the phase change model plays a key role in cryogenic fluid Computational Fluid Dynamics(CFD) simulation, the usage of reasonable phase change model will be important. Based on four different phase change theory, the commercial software FLUENT are used and four different phase change models are presented by user defined secondary developing code. A CFD research on liquid hydrogen evaporation in microgravity is present, comparing with NASA sounding rocket experiment. Finally, a reasonable phase change model is commended by comparing the pressurizing rate of the four models, which can be used in cryogenic fluid management simulation.

Cryogenic propellant; Phase change; Microgravity

1004-7182(2018)01-0036-05

10.7654/j.issn.1004-7182.20180107

V511

A

2016-12-14；

2017-02-20

王 夕（1989-），男，博士，工程师，主要研究方向为运载火箭总体设计