氢氧膨胀循环发动机启动仿真研究

翟一帆，罗巧军



氢氧膨胀循环发动机启动仿真研究

翟一帆，罗巧军

（北京航天动力研究所，北京，100076）

基于IRC方法对液体火箭发动机进行模块化建模，在此基础上搭建了闭式膨胀循环发动机启动仿真模型，对发动机的启动过程进行了研究。研究结果表明：仿真模型与试车数据吻合较好，仿真模型得到了验证，调节涡轮旁通阀的时序可以有效改善启动过程中燃烧室压力超调。

液体火箭发动机；闭式膨胀循环；启动仿真；动态仿真

0 引 言

随着中国航天事业的不断发展，愈发复杂的空间任务对发动机提出了新的要求，如推力大范围调节、多次重复启动等。发动机动态仿真，作为在发动机全生命周期中的重要技术手段，在诸如方案论证比较、故障模式研究、试验异常点寻因、系统性能优化等方面具有重要的作用。

启动过程中，发动机在很短时间内由初始状态爬升到主级工况，系统参数将发生大范围的剧烈变化。启动阶段的各组件工作在非稳态的恶劣条件下，极易发生故障，导致整个发动机系统出现问题。

本文采用一维分段集中参数方法[1]，使用AMESim软件进行模块化建模，建立了发动机关键组件的动态模块，并以此搭建闭式膨胀循环液体火箭发动机系统模型，针对发动机的启动过程进行仿真，并与试车数据进行了比较。

1 管路IRC方法

发动机系统是将各典型组件通过流体（液体或气体）管路串联而成的热力系统，流体管路的特性对发动机系统的动态特性具有重要影响。

在低频动力学范围内，流体管路的动力学模型主要采用集中参数模型的方法处理。集中参数模型虽然较为粗糙，但求解容易，因此在工程上得到广泛的应用。通过使用集中参数法，Kanmuri等[2]建模并分析了LE-5发动机的启动过程；Binder等[3]建立了RL10A-3-3A发动机的瞬态仿真模型；刘红军等[4]建模并分析了补燃循环发动机启动过程；陈宏玉等[5]建模并分析了补燃循环发动机推力调节过程。

IRC方法是以温度、压力、质量流量和焓流量为基本变量的一维单相流体控制方程的分段集中参数方法。对于发动机启动过程，在不用考虑中高频的振荡中IRC方法可以使用。

使用IRC方法，将管流在空间上进行有限个单元的划分，对单元采用集中参数处理，认为单元内流体的状态参数或运动参数是瞬时一致的和均匀的。

单元划分可分为状态单元和运动单元两种。状态单元内，流体的压力、密度、温度、内能等状态参数一致，称之为容性单元（C单元）；运动单元内，流体的运动速度一致，称之为（惯性）阻性单元（IR单元）。

使用IRC方法划分后，连续管路等效为C单元与IR单元交错串联形成的管路，如图1所示。

图1 一维流动IRC划分

C单元以质量流量、焓流量为输入量，以温度、压力为输出量；IR单元以温度、压力为输入量，以质量流量、焓流量为输出量。C单元与IR单元间参数传递过程如图2所示。

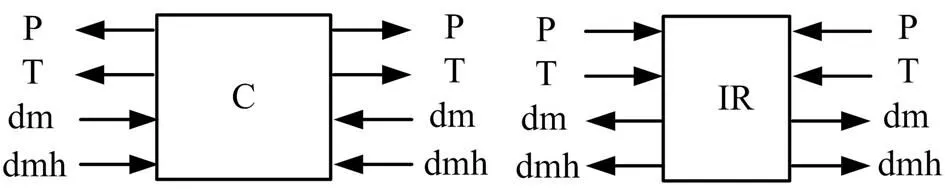
图2 C单元与IR单元参数传递过程示意

在运动单元（IR单元）内，若不考虑流体的压缩性，则单元退化为阻性单元（R单元）；若不考虑流体的流动损失，则单元退化为惯性单元（I单元）。

2 发动机组件的模块化建模

2.1 管 路

2.1.1 C单元

对管道某一选中单元，单元边界截面为固定截面，则一维质量守恒方程为

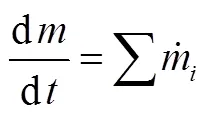
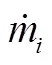
状态参数在单元中均匀分布，并假设管壁是刚性的，即不考虑容积变化，有：

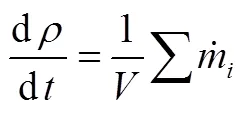
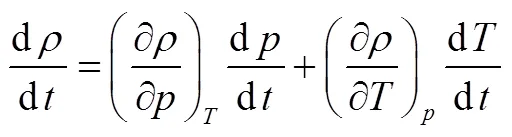
则：

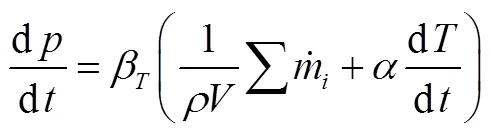
一维能量守恒方程为

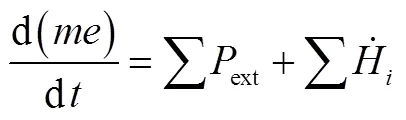
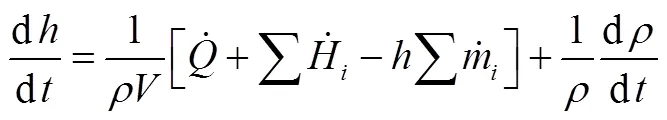
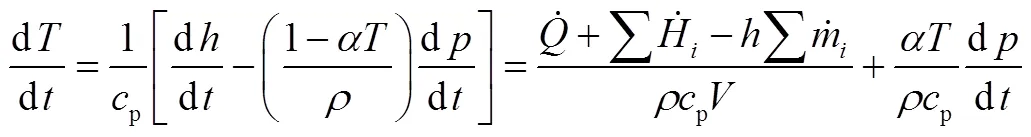
联立式（4）、式（7）可得到C单元计算式，即：

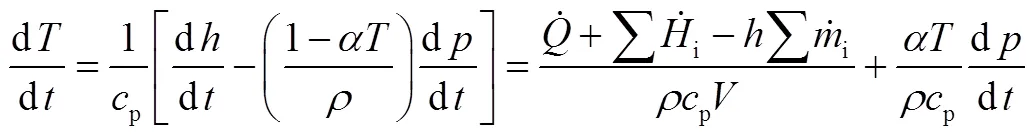
2.1.2 I单元

在发动机供应系统中，主要在不可压或弱可压流体单元中考虑流体的惯性，本节中假设单元工质为不可压缩流体。对管道某一选中单元，单元边界截面为固定截面，忽略摩擦，流路分段内动量方程为

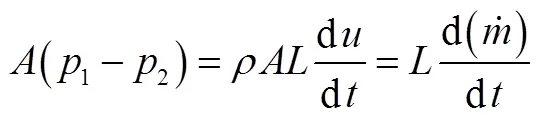
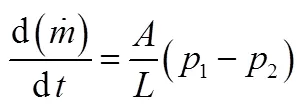
焓流量的计算为

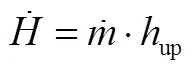
式中 下标up为入口参数。

2.1.3 R单元

a）对液路R单元，采用一般节流孔流量公式计算质量流量，即：

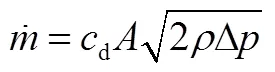
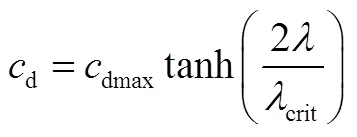
b）对气路R单元，采用声速喷嘴流量公式计算质量流量，即：

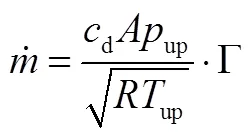
其中：

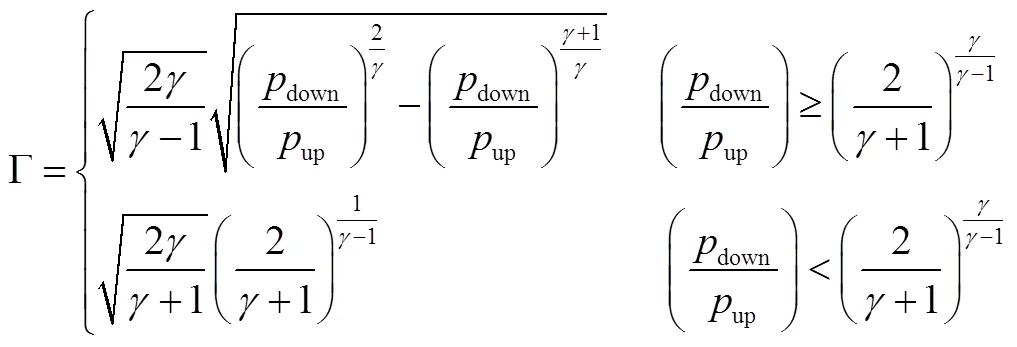
2.2 汽蚀管

汽蚀管属于节流件，因此使用R单元模型对之建模。式（12）未考虑汽蚀与非汽蚀的转换，因此汽蚀管质量流量使用下式计算：

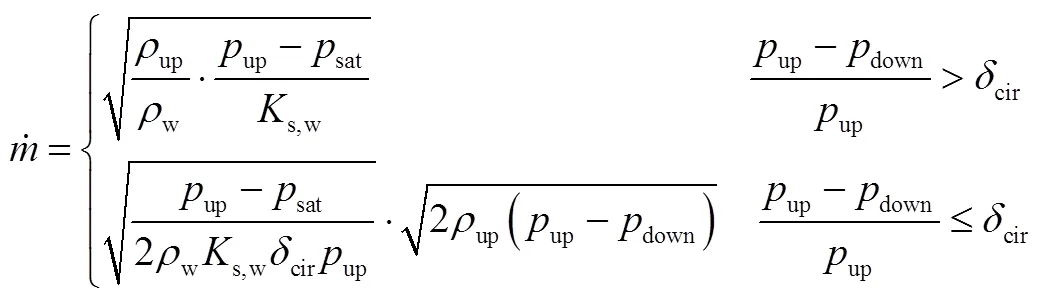
2.3 夹套冷却剂侧

考虑到工质为液氢，可能在夹套内升温气化过程中经历两相转变，因此使用两相流换热管道。在两相流换热管道中，主要讨论工质处于两相和单相（超临界）状态下的换热计算方法，并讨论单相流动中层流和湍流的不同。

2.3.1 单相流动

单相流动采用Gnielinski模型[6]计算对流换热系数，即：

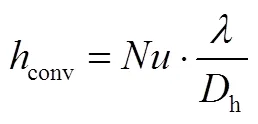
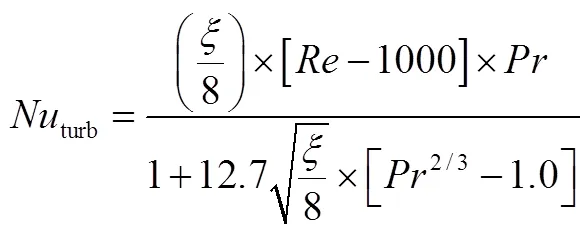
2.3.2 两相流动

两相流动不仅要考虑流动的层湍流情况，还要考虑液相在壁面沸腾或气相在壁面冷凝。

当壁面温度低于过流工质温度时，工质会在壁面冷凝。对于冷凝过程，对流换热系数采用Shah[8]相关系数计算，即：

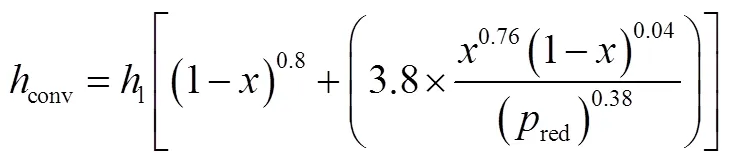
当壁面温度高于过流工质温度时，工质会在壁面沸腾。对于沸腾过程，对流换热系数采用VDI[9]模型计算，即：

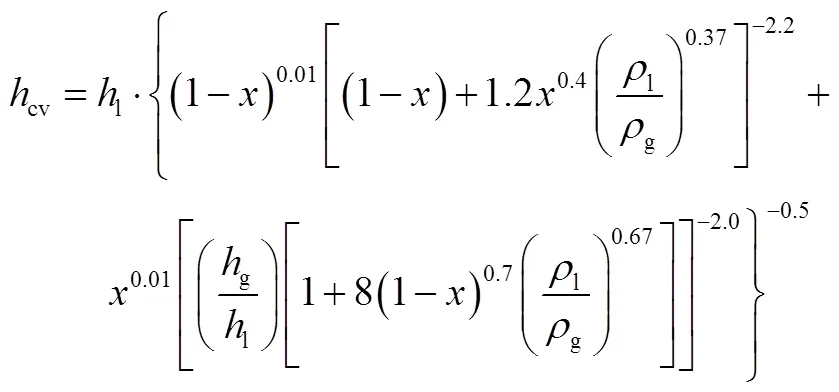
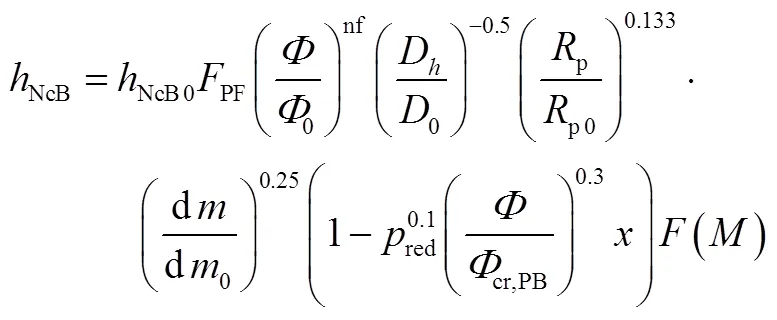
3 发动机系统模型

闭式膨胀循环发动机因为取消了预燃室和燃气发生器，因此系统简单、可靠性高。由于从再生冷却夹套引出的气氢温度不高，所以涡轮工作环境远优于分级燃烧循环和燃气发生器循环，涡轮泵系统研制技术难度低。

液氢从贮箱经氢泵增压后进入再生冷却系统吸收热量，出口吸热的气氢工质依次驱动氢、氧涡轮做功，通过转子带动泵工作，最后经过喷注器喷入推力室燃烧。液氧经氧泵增压后进入氧主汽蚀管，之后流经氧主阀通过喷注器喷入推力室燃烧。

液氢/液氧膨胀循环发动机系统示意如图3所示。

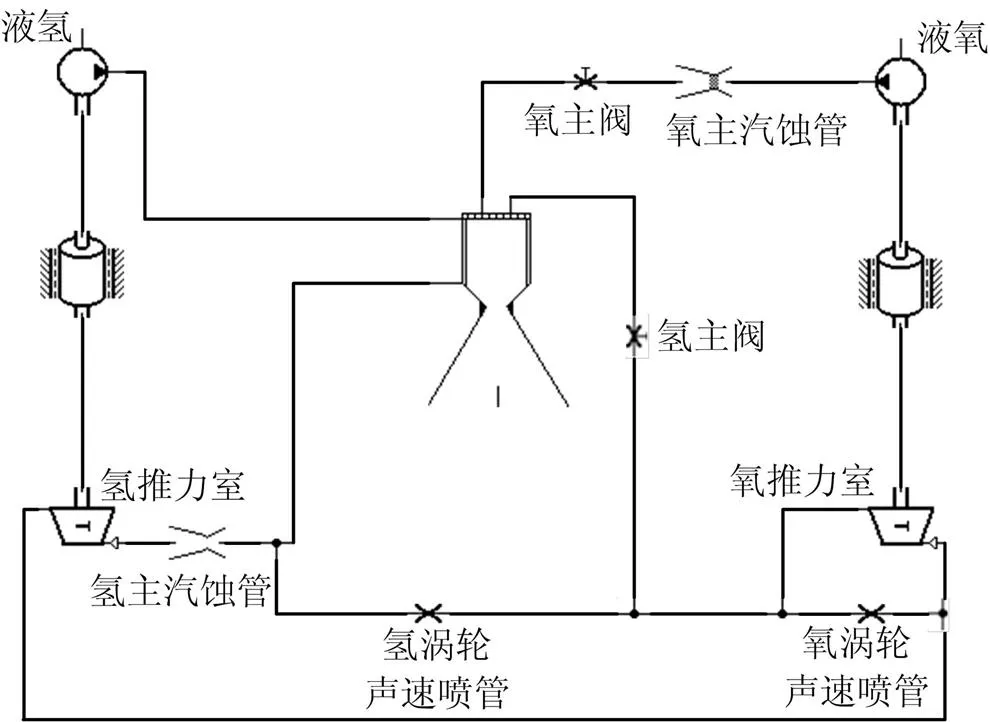
图3 闭式膨胀循环系统示意

使用AMESim软件进行建模，仿真模型如图4所示。

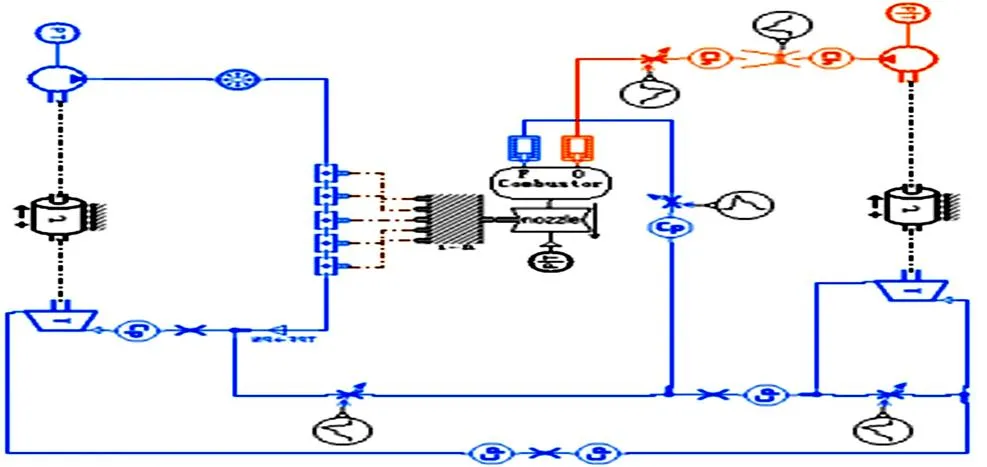
图4 AMESim仿真系统

4 仿真结果与分析

采用第3节建立的仿真模型，对某型发动机进行了启动仿真计算。

该发动机启动过程中，首先依靠推力室冷却夹套壁面的热容加热氢工质，夹套出口的气氢流经氢氧涡轮做功，推动两涡轮泵转子转速的爬升，然后氢氧流经喷注器喷入推力室燃烧，使室温升高。

以氢主阀打开时间为0 s，则点火器工作时间覆盖氢主阀打开时间，覆盖氢工质开始进入燃烧室的时间，且氧主阀早于氢主阀打开，氧主阀时序不用进行设计。考虑到阀门作动时间很短，将氢主阀打开视作一个阶跃信号输入，来对启动过程各动态指标进行计算。

启动过程的仿真结果与试车结果比较如图5所示。由图5可知，发动机启动仿真在爬升段吻合较好。

在启动初始段的压力平台仿真中，仿真模型未能仿真出实际情况，这主要是由于仿真模型中发动机各自动器组件如阀门等，使用的是准稳态模型，均未考虑其动态特性，同时，未考虑室压较低对燃烧效率和喷注器喷注效率的影响。

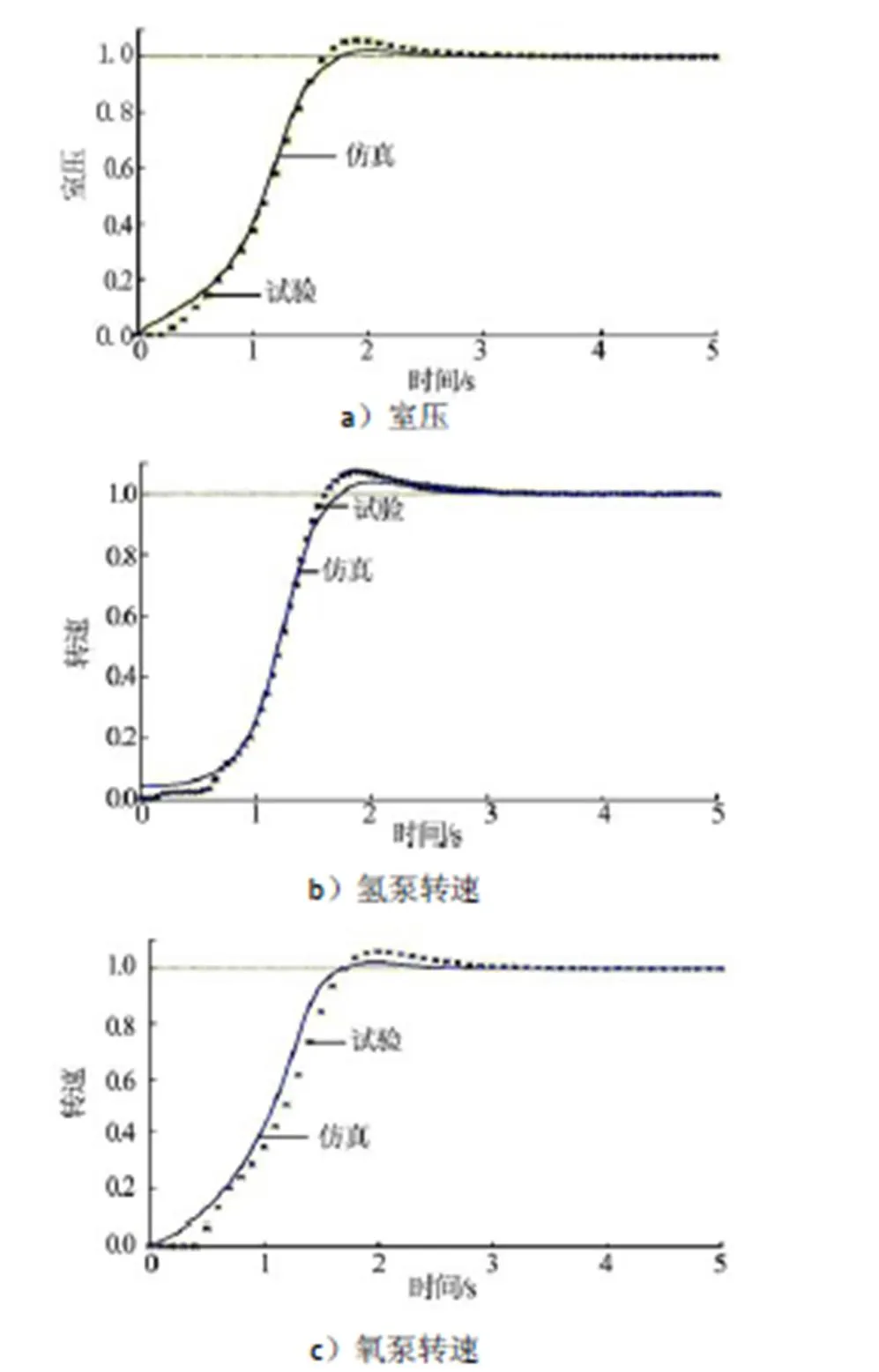
图5 仿真与试验结果对比曲线

在启动压力超调的仿真中，仿真模型也出现了压力超调。压力超调的出现主要是由涡轮泵系统的惯性引起，而且发动机中涡轮旁通采用声速喷嘴进行节流，无法调节开度。

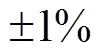
由图5a可知，仿真与试车都出现了启动压力超调，为了消除这个压力超调，将两涡轮旁通声速喷嘴以调节阀代替。设置阀门为三位阀（全关/半开/全开），其中半开为额定工况阀芯位置，阀门作动时间设置为50 ms。结果表明，设置阀门在1.55 s由全关转为全开，2.05 s由全开转为半开的时序，可成功消除启动压力超调。实际应用中，考虑到发动机散差，阀门全开、半开时序的设定应与室压相关联。

表1 仿真与试车结果动态参数比较

Tab.1 Dynamic Parameters Between Simulation and Trial

动态性能延迟时间/s上升时间/s峰值时间/s调节时间/s超调量 室压仿真1.200.832.020.567.32% 试车1.220.791.850.943.80% 氢泵转速仿真1.101.102.020.406.00% 试车1.20.91.90.92.34% 氧泵转速仿真1.801.021.970.382.31% 试车1.21.02.00.96.15%

该时序下发动机启动仿真与原启动仿真的对比如图6所示。

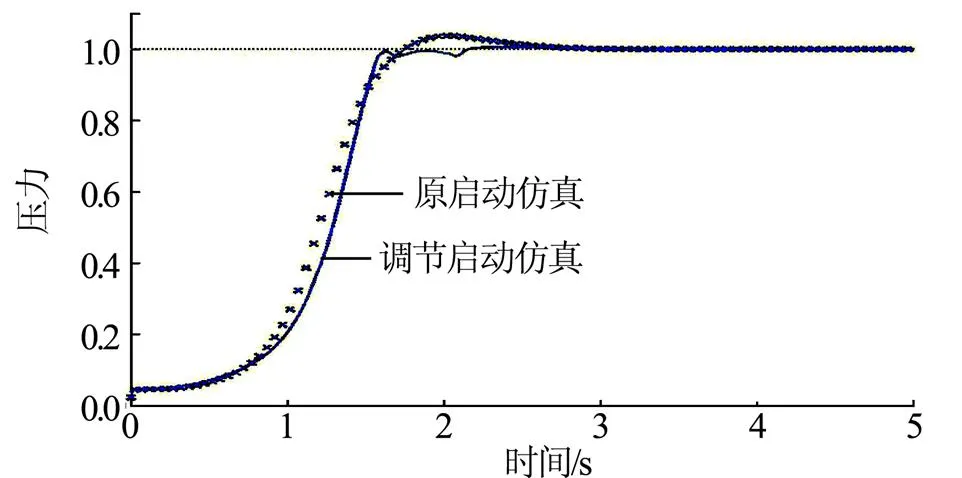
图6 设置调节阀消除启动压力超调曲线

由图6可知，使用两个涡轮旁通阀，并设置正确的时序方案，较原声速喷嘴方案，能够成功消除燃烧室启动压力超调。

5 结 论

本文使用基于IRC方法简化的仿真模型，对发动机组件进行了模块化建模。在此基础上，搭建了闭式膨胀循环发动机的启动仿真模型，结果与近期试车试验较为吻合。在仿真模型中，使用两个涡轮旁通调节阀代替声速喷嘴模型，发现可以通过设置正确的时序减小甚至完全消除启动压力超调。仿真模型的验证，可以进一步对发动机推力调节动态过程进行研究。

[1] 李锦江. 一种低温发动机系统动态仿真的快捷方法[J]. 导弹航天与运载技术, 2011(6): 13-17.

Li Jinjiang. An available technique for dynamic simulation of cryogenic rocket engines[J]. Missles and Space Vehicles, 2011(6): 13-17.

[2] Kanmuri A, et al. Start transient analysis of turbopum-fed LOX/LH2rocket engine(LE-5)[R]. N86-19371, 1983.

[3] Binder M P. A transient model of the RL-10A-3-3A rocket engine[R]. NASA CR-195478 (AIAA 95-2968), 1995.

[4] 刘红军, 等. 补燃循环发动机启动特性仿真研究[J]. 推进技术, 1999，20(3): 5-9.

Liu Hongjun, et al. Start-up simulation of a liquid propellant staged combustion rocket engine[J]. Journal of Propulsion Technology, 1999, 20(3): 5-9.

[5] 陈宏玉, 等. 补燃循环发动机推力调节过程建模与仿真研究[J]. 火箭推进, 2014, 40(1): 18-24.

Chen Hongyu, et al. Modeling and simulations on the thrust regulation process of staged combustion cycle rocket engine[J]. Journal of Rocket propulsion, 2014, 40(1): 18-24.

[6] Gnielinski V. New equations for heat mass transfer in turbulent pipe and channel flows[J]. International Chemical Engineering, 1976, 16(2): 359-368.

[7] Churchill S W. Friction factor equation spans all fluid flow regimes[J]. Chemical Engineering, 1977, 84(24): 91-92.

[8] Shah M M. A general correlation for heat transfer during film condensation inside pipes[J]. International Journal of Heat and Mass Transfer, 1979, 22(4): 547-556.

[9] Steiner D, Taborek J. Flow boiling heat transfer in vertical tubes correlated by an asymptotic model[J]. Hear Transfer Engineering, 1992, 13(2): 43-69.

[10] 胡寿松. 自动控制原理(第五版)[M]. 北京: 科学出版社, 2007.

Hu Shousong. Automatic control theoruy(5th edition)[M]. Beijing: Science Press, 2007.

Start-up Simulation of LOX/LH2Closed Expander Cycle Engine

Zhai Yi-fan, Luo Qiao-jun

(Beijing Aerospace Propulsion Institute, Beijing, 100076）

Based on IRC method, models of liquid rocket engine components are create. Then the closed expander-cycle engine start-up simulation model is set up. Rocket engine start-up process has been studied. Result shows that the simulation model matched the trial very well, the simulation model has been verified. By modulation of two turbo bypass valves, engine chamber start-up pressure peak is eliminated.

Liquid rocket engine; Closed expander cycle; Start-up simulation; Dynamic simulation

1004-7182(2018)01-0049-05

10.7654/j.issn.1004-7182.20180110

V43

A

2016-11-17；

2017-03-13

翟一帆（1993-），男，助理工程师，主要研究方向为液体火箭发动机系统