Geometrically exact nonlinear analysis of pre-twisted composite rotor blades

Li’n SHANG,Pinqi XIA,*,Dewey H.HODGES

aCollege of Aerospace Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China

bGuggenheim School of Aerospace Engineering,Georgia Institute of Technology,Atlanta,GA 30332,USA

1.Introduction

Modeling a pre-twisted composite rotor blade is complicated,not only because of the geometric non-linearity,but also because of the cross-sectional warping and the transverse shear deformation caused by anisotropic material properties.A pretwisted composite rotor blade was generally simplified into a one-dimensional beam analysis and two-dimensional crosssectional analysis.In the one-dimensional beam analysis,either a moderate deflection beam theory or a large deflection beam theory was adopted.The moderate deflection beam theory neglects the higher-order terms by an ordering analysis so that the strain-displacement relations and the relationship between the deformed coordinate and the undeformed coordinate can be expressed by the displacements and their derivatives.Hence,the established equations of motion are very complex,containing many terms.The large deflection beam theory does not use any restrictive hypothesis regarding deformations or angles other than a small-strain assumption.Thus,it can be used to solve problems of large deflections.In the two-dimensional cross-sectional analysis,a direct analysis method or a finite element method can be used.The direct analysis method is based on shell theory and usually is used to simplify a realistic composite blade to the form of a thinwalled or thick-walled beam.Hence,the direct analysis method is often used for preliminary design and/or optimization of composite blade.On the other hand,a finite element method can model realistic composite blades(e.g.,with foam-filled core,leading-edge weight,etc.)and is often used in detailed design.

Hong and Chopra1simplified a composite blade as a singlecell laminated beam to establish a composite blade model in which strain-displacement relations based on the moderate deflections by Hodges and Dowell2were used,and the shear stress through the thickness of the beam was neglected.Based on the modeling of Hong and Chopra,Panda and Chopra3studied the effect of elastic couplings on the dynamic characteristics of a blade in forward flight.Smith and Chopra4improved the model of Hong and Chopra1by including the torsion-related out-of-plane warping,transverse shear deformation and two-dimensional ply elasticity.By using the improved model,Smith and Chopra5,6established a hingeless rotor model to study the effects of elastic couplings caused by the tailoring of composite materials for improving the aeroelastic stability of rotor and reducing the vibratory load of rotor.Based on the aforementioned research,Chopra et al.7established a thick-walled composite blade model for arbitrary cross-sectional shape and material properties.

Hodges8established the geometrically exact nonlinear equations of motion for a one-dimensional beam by using Hamilton’s principle.Rodrigues parameters were used to express the finite rotation matrix of beam cross section.These established equations of motion can analyze large deflections.They included unknown variables for displacement,rotation,cross-sectional stress resultants,moment resultants,and linear and angular momenta.Hodges et al.9established a generalized classical beam model which is suitable for inhomogeneous,anisotropic,slender,prismatic beams by combining the rotation tensor decomposition method and the variational asymptotical method.The model consists of one-dimensional geometrically exact nonlinear beam analysis and twodimensional linear cross-sectional analysis.Except for the small strain assumption,no deformation and angle assumptions were adopted in the model.The transverse shear deformation, arbitrary cross-sectional warping and elastic couplings were considered in the model.Hence,the model can analyze large deflections.Cesnik10added the initial twist and curvature into the model established by Hodges et al.9and established both generalized classical and generalized Timoshenko beam models for analysis of both slender and arbitrary beams,respectively,by using different coordinate systems. Popescu11pointed out that the generalized Timoshenko beam model established by Cesnik10was not asymptotically correct,and established an approach to transform the generalized classical beam model into the asymptotically correct generalized Timoshenko beam model for prismatic beams by using the equilibrium equations and a minimization method.Yu12further improved the generalized Timoshenko beam model established by Popescu11by adding the initial twist and curvature into the model,using the more feasible perturbation method instead of a minimization method in the transforming process and eliminating the limitation that the beam axis must be chosen at the centroid of cross section.However,in the process of transforming the generalized classical beam model into the generalized Timoshenko beam model,Yu12neglected some higher-order terms in the expression of strain energy which may have nonnegligible effects for some beam structures.Based on the aforementioned research,Hodges13systematically improved the model for composite beams with arbitrary cross-sectional shape and material properties.Ho et al.14,15established the perturbation method including all transformation terms of the strain energy on the basis of research by Yu12,insuring the accuracy of the analysis.

Friedmann et al.16–18established a composite blade model for arbitrary cross-sectional shape and material properties based on finite element method.The model was based on the moderate deflection beam theory and considered the pretwist,transverse shear deformation and out-of-plane warping.Yin and Xiang19,20studied the effects of transverse shear and warping on rotor aeroelastic stability by using the method of Friedmann et al.16–18and analyzed the influence of elastic couplings on the aeroelastic response and loads of composite rotor in forward flight.Friedmann et al.21introduced the twodimensional cross-sectional analysis model developed by Hodges et al.13–15into the composite blade model which was based on the moderate deflection beam theory.Based on the improved formulations of Friedmann et al.21,Shi et al.22developed a modified 14 degree of freedoms beam element to predict the blade structural deformation.

In the above mentioned studies,several differences can be observed:(A)The cross section analyses by Chopra et al.1,4,7belong to the direct analysis method,and Hodges et al.13–15and Friedmann et al.16–18used the finite element method to perform the two-dimensional cross section analysis;(B)The one-dimensional beam analyses by Chopra et al.1,4,7and Friedmann et al.16–18were based on the moderate deflection beam theory,and Hodges et al.13–15used the large deflection beam theory to analyze the one-dimensional beam;(C)Chopra et al.1,4,7and Friedmann et al.16–18assumed the specific distributions of cross-sectional warping for composite blade,and Hodges et al.13–15transformed the geometrically nonlinear elastic analysis into the two-dimensional cross section analysis and the one-dimensional geometrically exact nonlinear analysis by using the variational asymptotical method and determined the arbitrary warping of beam cross section during the transforming process.Therefore,compared with the models of composite blade by Chopra et al.1,4,7and Friedmann et al.16–18,the generalized Timoshenko beam model by Hodges et al.13–15is more suitable for modeling composite blades.

In this paper,the geometrically exact nonlinear modeling for the generalized Timoshenko beam with arbitrary crosssectional shape,generally anisotropic material behavior and large deflection has been presented based on the Hodges’method.The concept of decomposition of rotation tensor was used to calculate the strain at an arbitrary point in the beam.The variational asymptotical method was used to determine the arbitrary warping of beam cross section.The generalized Timoshenko strain energy was derived from the equilibrium equations and the second-order asymptotically correct strain energy.Hamilton’s principle was used to establish the geometrically exact nonlinear equations of motion of beam.In the process of transforming the second-order asymptotically correct strain energy into the generalized Timoshenko strain energy,the two assumptions adopted by Yu12are abandoned and the second-order asymptotically correct strain energy is transformed into the generalized Timoshenko strain energy more accurately by using the perturbation method of Hodges et al.15The established model of beam was used to analyze the static and dynamic behavior of pre-twisted composite blades and compare with the experimental data by Bao and Chopra23–26for verifying the modeling method.The influences of transverse shear deformation on the static deformation and natural frequencies of the pre-twisted composite blade were analyzed.

2.Geometrically exact modeling of generalized Timoshenko beam

2.1.Geometrically nonlinear elastic analysis

to describe the beam deformation.The orthogonal unit base vectors corresponding to frames A,b and T are Ai,biand Ti(i=1,2,3)respectively as shown in Fig.1.b1is tangent torand b2,b3are along the coordinate axesx2,x3.T1is tangent toR,meaning that the transverse shear deformation is classified as part of the warping field.

It is supposed that a pointQon the undeformed beam reference linerhas the position vector r relative to a fixed pointPin frame A,and then an arbitrary point in the undeformed cross section at the pointQhas the position vector^r relative to the pointP,and^r is given by

The schematic of beam deformation is shown in Fig.1.x1is the arc-length coordinate along the undeformed beam reference liner.S（x1）denotes the cross section at an arbitrary point on the reference linerand its normal line is tangent tor.The point coordinates in the cross sectionS（x1）are denoted asx2,x3.sis the arc-length coordinate along the deformed beam reference lineR.Absolute deformation frame A,local undeformed frame b and local deformed frame T are introduced

Fig.1 Schematic of beam deformation.

where the subscript α=2,3.If a point with the position vector r before deformation has the position vector R after deformation,and a point with the position vector^r before deformation has the position vector^R after deformation,then^R can be expressed as

The displacement field expressed by Eq.(2)has four redundant degrees of freedom.To uniquely determine the displacement field,the following four constraints are applied to the cross-sectional warping:

In Eq.(3),w= ［w1,w2,w3］TandSis the area of the reference cross section.The constraints expressed by Eq.(3)mean that the cross sectional warping does not produce the rigid body displacements of the cross section and the rigid body rotation of the cross section around vector T1.

The classical one-dimensional generalized strains are defined as

In Eq.(5), （·）′denotes the derivative with respect tox1.k=kibiand¯K=¯KiTiare the curvature vectors of the undeformed beam and the deformed beam respectively.¯γ11,¯κ1,¯κ2and¯κ3are the classical one-dimensional generalized strains corresponding to the extension,twist and two directional elastic bending respectively.Let¯ε=［¯γ11,¯κ1,¯κ2,¯κ3］T.

In terms of Eqs.(1),(2),(5)and(6),the three-dimensional Jaumann-Biot-Cauchy strain of an arbitrary point in the beam can be calculated by using the decomposition of rotation tensor method.26The strain’s expression in the frame b is

where Γ = ［Γ11,2Γ12,2Γ13,Γ22,2Γ23,Γ33］Tand the detailed expressions of the coefficient matrices can be found in Ref.13.

2.2.Second-order asymptotically correct strain energy

From the strain by Eq.(7),the strain energy of the cross section can be expressed as

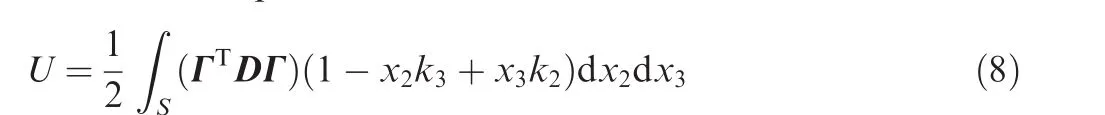
where D denotes the stiffness coefficient matrix of the material.

To establish the beam model suitable for arbitrary crosssectional shape and material property,the finite element method is used to discretize the cross-sectional warping field:

where N（x2,x3）is the shape function matrix and V（x1）denotes the vector consisting of all unknown nodal warping in the cross section.Then,the strain energy of the cross section can be further expressed as

where the detailed expressions of the matrix E and the matrices D with subscripts can be found in Ref.13.

The matrix ψ in Eq.(4)can be discretized by using the same shape function matrix N（x2,x3）,i.e.ψ =N（x2,x3）Ψ,and then the constraints Eq.(3)become

Determining the warping vector V（x1）by using the variational asymptotical method and minimizing the strain energy of Eq.(10)under the constraints Eq.(11),unknown nodal warping vector of the cross section and the second-order asymptotically correct strain energy are expressed respectively as

2.3.Generalized Timoshenko strain energy

In this section,the Timoshenko one-dimensional generalized strains containing one-dimensional generalized transverse shear strains are introduced. Then, the generalized Timoshenko strain energy is derived from the second-order asymptotically correct strain energy in terms of the equilibrium equations and the relationships between the Timoshenko onedimensional generalized strains and the classical onedimensional generalized strains.

Local deformed frame B with orthogonal unit base vectors Biis introduced at an arbitrary point on the reference lineRof beam after deformation.B1is normal to the reference cross section after deformation.The Timoshenko one-dimensional generalized strains are defined as

From the definitions of the classical one-dimensional generalized strains and the Timoshenko one-dimensional generalized strains,the relationships among ¯ε, ε and γscan be expressed as

Substituting Eq.(16)into Eq.(13),the second-order asymptotically correct strain energy expressed by the Timoshenko one-dimensional generalized strains ε and γscan be obtained as

The standard expressional form of generalized Timoshenko strain energy is

Combining Eqs.(17),(18)and equilibrium equations and solving a set of nonlinear equations containing the unknown matrices X,Y and G by the perturbation method of Ho et al.,15the generalized Timoshenko strain energy expressed by Eq.(18)can be obtained.

2.4.Geometrically exact nonlinear equations of motion and their solutions

In this section,the Hamilton’s generalized principle is used to derive the one-dimensional geometrically exact nonlinear equations of motion:

whereTandUare the kinetic and strain energy per unit length of the beam respectively,δ¯Wis the virtual work of external loads per unit length,and δ¯Λ is the virtual action at the ends of the beam and at the ends of the time interval.The strain energy per unit length has been described in Sections 2.2 and 2.3.The expressions of the velocities and the kinetic energy per unit length are described as follows.

The velocity of an arbitrary pointMin the beam can be expressed as

From Eqs.(20)–(22),the kinetic energy per unit length can be expressed as

where ρ is the density of the material,and Δ is the identity matrix of the 3rd order.

In Eqs.(26)–(28),γ= ［γ11,2γ12,2γ13］T,κ = ［κ1, κ2, κ3］T,S is the stiffness matrix of beam cross section,FB,MB,PBand HBare the cross-sectional stress resultant,moment resultant,linear momenta and angular momenta in the frame B respectively.The Rodrigues parameters θAare used to express the finite rotation matrix C of the beam cross section.The physical meanings and the detailed expressions of the parameters which are not introduced in Eq.(25)can be seen in Ref.13.

The equations of motion by Eq.(25)can be solved by using the finite element method.Dividing the beam intoNelements,and conducting the discretization and simplification,a set of equations are obtained as

3.Analysis of pre-twisted composite blades

In this section,the modeling method described in Section 2 is applied to analysis of pre-twisted composite blades designed and tested by Bao and Chopra.23–26The obtained theoretical results are compared with experimental data to validate the accuracy of present modeling method for analysis of a pretwisted composite blade.Then,the static analysis of pretwisted composite blades is extended to a large deflection analysis to demonstrate that the present modeling method can be used for analysis of pre-twisted composite blades with large deflections.It is noted that the present method has some advantages over the beam approach of Ref.25:(A)The present method can exactly model a realistic composite blade with filled foam core and leading-edge weight as shown in Fig.2 through the discretization of the blade cross section by using the finite element method as Eq.(9),while the beam approach of Ref.24,which is the method presented in Ref.7,is based on the shell theory and can only model the parts of the blade cross section which can be simplified as shell elements.(B)For the present method,the detailed three-dimensional stresses can be recovered by using Eqs.(7),(9),(12),(16)and(26),and the obtained cross-sectional stress resultant FBand moment resultant MB,while for the beam approach of Ref.25,the strain-displacement relation for the wall of a cylindrical shell of arbitrary geometry is used to obtain the strains.Hence,the present method can accurately recover the detailed threedimensional stresses.(C)The present method is geometrically exact and can be used for solving the large deflection problems such as the numerical analyses shown later,while the beam approach of Ref.25can only handle moderate deflection prob-lems because higher-order terms are neglected based on an ordering scheme.

Bao and Chopra23–26designed five Mach scale pre-twisted composite blades and measured the tip flapwise bending slope and twist of these blades.The tested blade was cantilevered at root and loaded with tip flapwise bending force or torque as shown in Fig.2(a).The cross section of the blade consisted of an IM7/8552 graphite/epoxy D-spar,IM7/8552 graphite/epoxy weave skin,IM7/8552 graphite/epoxy web,Rohacell IG-71 fore cell foam core and Rohacell IG-31 aft cell foam core as shown in Fig.2(b).At some spanwise locations along the blade,the tungsten alloy leading-edge weights with airfoil profiles were embedded in the blade to shift the blade crosssectional center of gravity to the aerodynamic center.The main geometry parameters of these blades are given in Table 1.The five pre-twisted composite blades correspond,respectively,to zero coupling between flap-bending and torsion(FBT-0),positive coupling between flap-bending and torsion(FBT-P),negative coupling between flap-bending and torsion(FBTN),two segmented coupling between flap-bending and torsion(FBT-P/N:positive outboard,negative inboard)and three segmented coupling between flap-bending and torsion(FBT-P/0/N:positive outboard,uncoupled midspan,negative inboard).The elastic couplings were caused by the layup of the D-spar.The positive coupling between flap-bending and torsion refers to the situation that the upward flap-bending causes the nose down twist.The detailed layup of the blades is listed in Table 2.

The measured and predicted tip flapwise bending slope and twist of FBT-0 and FBT-P blades under the tip flapwise bending force and torque are shown in Figs.3 and 4 respectively.It can be seen from Figs.3 and 4 that the calculated results agree very well with the experimental results.Also,according to the calculated results and the comparisons with the experimental results by the authors,the correlations between the calculated and experimental results of the other composite blades were very well,which verifies the accuracy of present modeling for static analysis of pre-twisted composite blade.For the FBT-0 blade,there was no twist under tip flapwise bending force and no bend under tip torque.The tip twist magnitudes of the FBT-P and FBT-N blades under the same tip flapwise bending force were almost the same but the directions of the twist were opposite;the tip flapwise bending slope magnitudes of the FBT-P and FBT-N blades under the same tip torque were almost the same but the directions of the slope were opposite.The coupling relations between flapwise-bending and torsion of the FBT-P/N and FBT-P/0/N blades were the same as that of FBT-N blade,but the coupling magnitudes of the three blades were different.Hence,the composite blades can be designed through the layup of D-spar to obtain the desired elastic couplings.

Bao and Chopra23–26mounted the five pre-twisted composite blades on an articulated rotor hub28and measured the fundamental torsional frequencies for the non-rotating case.In this paper,the fan plots of the pre-twisted composite blades were predicted by using the present modeling with the same boundary conditions.Because there is elastic coupling in the blades,each natural frequency corresponds to a mode shape that consists of one or more types of motion.Here,a frequency is named in accordance with the dominant motion in the associated mode shape.The predicted fan plot and the measured fundamental torsional frequency for the nonrotating FBT-0 blade are shown in Fig.5.The predicted fundamental torsional frequency for the non-rotating FBT-0 blade is 182 Hz which is close to the measured frequency 186 Hz,with 2.1%error.According to the calculations by the authors,the predicted fundamental torsional frequencies of the other pre-twisted composite blades in non-rotating situation are also close to the measured frequencies,which verifies the dynamic analysis accuracy of present modeling for a pre-twisted composite blade.It should be noted that for pre-twisted composite blades analyzed in this paper,the rotational speed 2300 r/min corresponds to the tip velocity 220 m/s which is a normal tip velocity of the blade.From Fig.5,the blade natural frequencies are inconsistent with the rotating frequency and its multiples at the rotational speed 2300 r/min of the blade.Hence,there is no resonance of the blade at the rotational speed 2300 r/min.

Fig.2 Schematic of composite blade.

Table 1 Main geometry parameters of composite blade.

Table 2 Layup of composite blades.

The static nonlinear large deflection responses of the pretwisted composite blades under tip flapwise bending force and torque were calculated.The calculated nonlinear tip flap-bending deflections of FBT-P and FBT-P/0/N blades are shown in Figs.6 and 7,respectively.The calculated linear results are also plotted in Figs.6 and 7 for comparison.According to the calculations by the authors,the tip flapbending deflections of the other pre-twisted composite blades are similar to those of FBT-P and FBT-P/0/N blades.

Fig.3 Tip flapwise bending slope and twist of FBT-0 blade.

Fig.4 Tip flapwise bending slope and twist of FBT-P blade.

4.Influence of transverse shear deformation

The influence of the Transverse Shear Deformation(TSD)is from the 6×6 fully coupled stiffness matrix of the blade cross section.To ignore the influence of the TSD,the cross-sectional stiffness matrix can be changed to a 4×4 reduced stiffness matrix by the following operational steps:(A)inverting the fully coupled stiffness matrix to obtain a flexibility matrix;(B)ignoring the rows and columns corresponding to one-dimensional generalized transverse shear strain in the flexibility matrix to obtain a reduced 4×4 flexibility matrix;(C)inverting the 4×4 reduced flexibility matrix to obtain a 4×4 reduced stiffness matrix.In this section,the pre-twisted composite blades designed and tested by Bao and Chopra23–26were used to study the influence of the transverse shear deformation.

For the FBT-0 and FBT-P blades,the calculated static responses without and with the TSD are almost the same as shown in Figs.3 and 4.According to the calculations by the authors,the influences of the TSD on the other pre-twisted composite blades are similar to those on the FBT-0 and FBT-P blades.Hence,the TSD has little influence on the static responses of the pre-twisted composite blades.It has been known that the influence of TSD is related to the length to chord ratio of the blade.To further investigate the TSD,the static responses without and with TSD were calculated with different length to chord ratios of the blade.The length to chord ratio of the blade was varied by changing the length of the blade and retaining the cross section size and material distribution of the blade.The blades were loaded by tip flapwise bending force 2.5 N or tip torque 0.4 N·m.The ratios of tip flap-bending deformation without the TSD to that with the TSD via length to chord ratios of the blade for the FBTP and FBT-N blades are shown in Figs.8 and 9,respectively.It can be seen from Figs.8 and 9 that the influence of the TSD reduces gradually with the increase of the length to chord ratio of the blade.The calculated results of the other pre-twisted composite blades are similar to those of the FBT-P and FBT-N blades.

The length to chord ratio of the pre-twisted composite blades designed and tested by Bao and Chopra23–26is 11.5.Hence,the influences of the TSD on the blades are very small as the calculated results in this paper.Therefore,the influence of TSD on the static response of pre-twisted composite blades is related to the length to chord ratio of the blade.When the ratio is sufficiently large,the influence of TSD can be neglected and the 6×6 fully coupled stiffness matrix can be replaced with the 4×4 reduced stiffness matrix to calculate the static response of the blade.

The caused percentage errors of the first five flap frequencies,the first four lag frequencies and the first torsion frequency of the FBT-0 and FBT-N blades by neglecting the TSD are listed in Table3.The error is defined by|ωns- ωs|/ωs× 100%,where ωsand ωnsare the frequencies of the blades with and without TSD respectively.It can be seen from Table 3 that the TSD has little influence on the lower frequencies of the FBT-0 and FBT-N blades except for the first two natural frequencies which are corresponding to the rigid body lag and flap and not affected by the TSD.For a certain rotational speed,the influences of the TSD and the errors of the natural frequencies increase gradually with the increase of the order of the mode.According to the calculations by the authors,the influences of TSD on the other pre-twisted composite blades are similar to those on the FBT-0 and FBT-N blades.

Fig.5 Fan plot of FBT-0 blade.

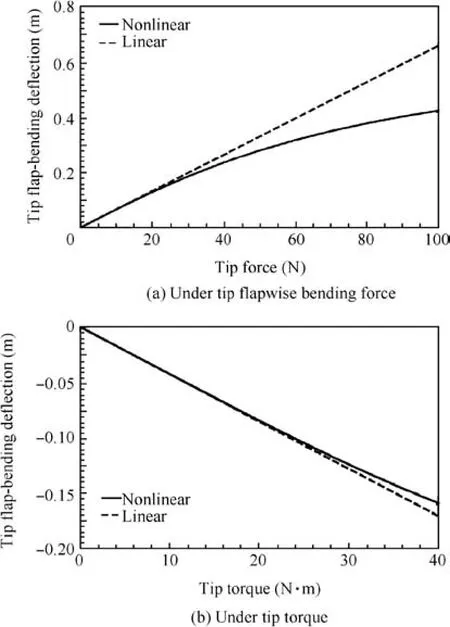
Fig.6 Calculated static tip deflection of FBT-P blade.

Fig.7 Calculated static tip deflection of FBT-P/0/N blade.

To further investigate the effect of TSD on the natural frequencies,the caused errors of the natural frequencies by ignoring the TSD were calculated at different lengths of the blade while retaining the cross section size and material distribution of the blade.The errors of the first five flap frequencies,the first four lag frequencies and the first torsion frequency for the FBT-P blade are listed in Table 4.For a certain length of the blade,the errors increase gradually with the increase of the order of the mode.For a certain cross section of the blade,the errors increase gradually with the decrease of the length of the blade.The natural frequency errors of the other pre-twisted composite blades at different blade lengths are similar to those of FBT-P blade.

Fig.8 Tip flap-bending deformation ratios without TSD to that with TSD for FBT-P blade.

Fig.9 Tip flap-bending deformation ratios without TSD to that with TSD for FBT-N blade.

Table 3 Frequency errors caused by neglecting TSD at different rotational speeds.

Table 4 Frequency errors of FBT-P blade caused by neglecting TSD at different blade lengths.

5.Conclusions

(1)The modeling for geometrically exact nonlinear static and dynamic analyses of generalized Timoshenko beam with arbitrary cross-sectional shape,generally anisotropic material behavior and large deflection has been presented and applied to the static and dynamic analysis of the five pre-twisted composite blades.The analytical accuracy has been validated by consistent correlation of the calculated results with experimental data for the five pre-twisted composite blades.The desired elastic couplings of pre-twisted compositeblades can be achieved by the proper layup of the blade D-spar.

(2)The effects of the transverse shear deformation on the static deformation and natural frequency of pretwisted composite blades are related to the length to chord ratio of the blade and reduce gradually with the increase of the length to chord ratio of the blade.The errors in the natural frequencies caused by neglecting transverse shear deformation increase gradually with the increase of the order of the mode.When the ratio is sufficiently large,the influence of transverse shear deformation can be neglected,and the 6×6 fully coupled stiffness matrix can be replaced with the 4×4 reduced stiffness matrix to calculate the static responses and the lower blade natural frequencies.

Acknowledgment

This study was supported by the National Natural Science Foundation of China(No.11572150).

1.Hong CH,Chopra I.Aeroelastic stability analysis of a composite rotor blade.J Am Helicopter Soc1985;30(2):57–67.

2.Hodges DH,Dowell EH.Nonlinear equations of motion for the elastic bending and torsion of twisted nonuniform rotor blades.Moffett Field:Ames Research Center and U.S.Army Air Mobility R&D Laboratory;1974.Report No.:NASA TN D-7818.

3.Panda B,Chopra I.Aeroelastic stability of a composite blade in forward flight.Vertica1987;11(1):187–210.

4.Smith EC,Chopra I.Formulation and evaluation of an analytical model for composite box-beams.J Am Helicopter Soc1990;36(3):23–35.

5.Smith EC,Chopra I.Aeroelastic response,loads and stability of a composite rotor in forward flight.AIAA J1993;31(7):1265–73.

6.Smith EC,Chopra I.Air and ground resonance of helicopters with elastically tailored composite rotor blades.J Am Helicopter Soc1993;38(4):50–61.

7.Jung SN,Nagaraj VT,Chopra I.Re fined structural model for thin and thick-walled composite rotor blades.AIAA J2002;40(1):105–16.

8.Hodges DH.A mixed variational formulation based on exact intrinsic equations for dynamics of moving beams.Int J Solids Struct1990;26(11):1253–73.

9.Hodges DH,Atilgan AR,Cesnik CES,Fulton MV.On a simplified strain energy function for geometrically nonlinear behavior of anisotropic beams.Compos Eng1992;2(5–7):513–26.

10.Cesnik CES.Cross-sectional analysis of initially twisted and curved composite beamsDissertation.Atlanta:Georgia Institute of Technology;1994.p.27–69.

11.Popescu B.Asymptotically correct refinements in numerical crosssectional analysis of composite beams[dissertation].Atlanta:Georgia Institute of Technology;1998.p.13-75.

12.Yu W.Variational asymptotic modeling of composite dimensionally reducible structures[dissertation].Atlanta:Georgia Institute of Technology;2002.p.21-91.

13.Hodges DH.Nonlinear composite beam theory.Reston:AIAA;2006.p.35–141.

14.Ho J,Hodges DH,Yu W.Energy transformation to generalized Timoshenko form for nonuniform beams.AIAA J2010;48(6):1268–72.

15.Yu W,Hodges DH,Ho J.Variational asymptotic beam sectional analysis—An updated version.Int J Eng Sci2012;59(10):40–64.

16.Yuan K,Friedmann P,Venkatesan C.A new aeroelastic model for composite rotor blades with straight and swept tips.Proceedings of the 33rd AIAA/AHS/ASME/ASCE/ASC structures,structural dynamics&materials conference;1992 Apr 13;Dallas,USA.Reston:AIAA;1992.

17.Yuan K,Friedmann P,Venkatesan C.Aeroelastic behavior of composite rotor blades with swept tips.Proceedings of the American Helicopter Society 48th annual forum;1992 Jun 3-5;Washington,D.C.,USA.Fairfax:American Helicopter Society;1992.

18.Yuan K,Friedmann P,Venkatesan C.Aeroelastic stability response and loads of swept tip composite rotor blades in forward flight.Proceedings of the 35th AIAA/AHS/ASME/ASCE/ASC structures,structural dynamics&materials conference;1994 Apr 18;Hilton Head,USA.Reston:AIAA;1994.

19.Yin W,Xiang J.Aeroelastic stability for helicopter rotor blades with consideration of transverse shear deformation and warping.ActaAeronauticaetAstronauticaSinica2006;27(6):1130–4[Chinese].

20.Yin W,Xiang J.Aeroelastic response and hub load of composite hingeless rotor in forward flight with elastic couplings.Acta Aeronautica et Astronautica Sinica2007;28(3):605–9[Chinese].

21.Friedmann P,Glaz B,Palacios P.A moderate de flection composite helicopter rotor blade model with an improved cross-sectional analysis.Int J Solids Struct2008;46(10):2186–200.

22.Shi Y,Xu Y,Xu G,Wei P.A coupling VWM/CFD/CSD method for rotor airload prediction.Chin J Aeronaut2017;30(1):204–15.

23.Bao J,Nagaraj VT,Chopra I.Design and hover test of low vibration Mach scale rotor with twisted composite tailored blades.Proceedings of the 44th AIAA/ASME/ASCE/AHS structures,structural dynamics&materials conference;2003 Apr 7;Norfolk,USA.Reston:AIAA;2003.

24.Bao J.Development of Mach scale rotors with composite tailored couplings for vibration reduction[dissertation].College Park:University of Maryland;2004.p.54-150.

25.Bao J,Nagaraj VT,Chopra I.Development of Mach scale rotors with tailored composite coupling for vibration reduction.J Aircraft2006;43(4):922–31.

26.Bao J,Nagaraj VT,Chopra I.Wind tunnel test of five sets of Mach scale composite tailored rotor with flap-bending/torsion couplings for vibration reduction.J Am Helicopter Soc2008;53(3):215–25.

27.Danielson DA,Hodges DH.Nonlinear beam kinematics by decomposition of the rotation tensor.J Appl Mech1987;54(2):258–62.

28.Bi NP.Contributions to the experimental investigation of rotor/-body aerodynamic interactions[dissertation].College Park:University of Maryland;1991.p.108.