A self-similar solution of a curved shock wave and its time-dependent force variation for a starting flat plate airfoil in supersonic flow

Zijun CHEN,Jing LIN,Chenyun BAI,b,Ziniu WU,b,*

aDepartment of Engineering Mechanics,Tsinghua University,Beijing 100084,China

bInstitute of Aeroengine,Tsinghua University,Beijing 100084,China

1.Introduction

In some flight problems,a wing may involve a sudden unsteady motion,for example,a sudden acceleration from rest or a sudden change of angle of attack in a steady flow.This may come from motions of command surfaces,1,2or step motions due to aeroelasticity3or striking of gust.4,5Essential flow characteristics and force behaviors may be studied as those of a starting flow problem.6Seen from a body- fixed frame,the initial flow is uniform,but the fluid velocity normal to the surface of the wing suddenly vanishes.Generation of free vortices and acoustic or shock waves makes the flow unsteady,and the force is highly time-dependent(see for Refs.7,8).

The supersonic starting flow of a flat plate at a small angle of attack was studied long ago by Heaslet and Lomax.6By regarding the time as an equivalent space direction,they obtained a linear wave equation and found the exact solutions for the pressure and time-dependent lift coefficient.Lomax et al.9then extended the linear theory to consider the indicial lift of two-or three-dimensional wings at both subsonic and supersonic flow speeds.Lengthy expressions were provided for the calculation of the pressure and indicial functions of lift and moments.The pressure load and the time-dependent aerodynamic response to a step change in an airfoil motion have also been of great concerns in aeroelasticity applications.10–14

According to Heaslet and Lomax,6for a small angle of attack,there is an unsteady Mach wave(simple wave)generated from the surface of a flat plate,and the windward side is a compressive wave while the leeward side is an expansion wave,both of which can be given by the inviscid piston theory.15–17In the meantime,there is a leading edge steady Mach wave on both sides of the plate.Between the wall and these Mach waves,the flow is uniform.The interaction between these steady and unsteady waves leads to a secondary wave on both sides of the plate,and each secondary wave gives a non-uniform flow.

Recently,Bai and Wu18,19extended the solution of Heaslet and Lomax6to a high angle of attack.As shown in Fig.1 for a specific flow condition,below the plate,we have a straight oblique shock wave and an unsteady horizontal shock wave(Ma∞is the freestream Mach number,α is the angle of attack,V∞is the velocity of freestream,and τ is the dimensionless time).The flow between these waves and the wall is uniform.Between these waves,there is a secondary shock wave,and the flow between the secondary shock wave and the wall is uniform.

Above the plate,there is a steady Prandtl-Meyer wave and a vertically-moving rarefaction wave.The flow between these waves and the wall is uniform.Between these waves,there is a secondary rarefaction wave,and the flow between this secondary wave and the wall is uniform.

In the linear case,Heaslet and Lomax6gave an analytical solution which was then modified by Bai and Wu19to take into account the effects of shock waves and rarefaction waves in the uniform-flow regions.Fig.1(a)and Fig.2 display a typical flow structure and force evolution in time(cAis the chord length,Cpis the pressure coefficient,Cnis the normal force coefficient).It is seen that the secondary wave is a local expansion on the windward side and a local compression wave on the leeward side.The normal force is nearly constant in time during an initial period,then increases following a curve with a change of slope,and finally reaches a steady state value.

There are two problems that remain unstudied.The first is the structure of the curved shock wave.The second is the mechanism by which the force exhibits near constancy for an initial period of time.Moreover,the reason that the force curve changes slope at various stages has not been identified.

In this paper,we will build a self-similar solution for the secondary(shock)wave and use such a solution to explain the initial force behavior.We also give characteristic times at which the force curve changes slope.The present paper is restricted to a theoretical study for inviscid flow.

In Section 2,the solutions in the uniform regions given by Heaslet and Lomax6and Bai and Wu19are briefly recalled.In Section 3,we will derive the curved shock solution in a nonlinear case,using similarity assumption.The analytical solution will be compared to the numerical solution by CFD.In Section 4,we study the mechanism by which the initial period of the force curve is almost constant,and provide the characteristic times at which the force curve changes slope.

2.Solutions in uniform flow regions and characteristic wave speeds

Fig.1 Supersonic starting flow(the flow involves a steady Oblique Shock Wave(OSW)and a Prandtl-Meyer expansion Wave(PMW)from the leading edge,a vertically-moving Normal Shock Wave(NSW)below the plate,and a vertically-moving Rarefaction Wave(RW)above the plate.The interaction between the steady and unsteady waves leads to secondary waves(region 5 and region 6).In a linear case,these waves degenerate to Mach waves).

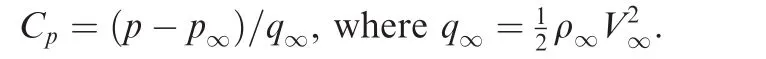
Fig.2 CFD solution of starting flow at Ma∞ =2,α =10° (the number of chords traveled).

For a linear case,the solution was given by Heaslet and Lomax.6For a nonlinear case,the solution was given by Bai and Wu.18,19

For a linear case,the flow on both sides of a plate(of chord lengthcA)is divided into three regions:Regions I,II,and III.These regions are bounded by the characteristic linesx= （u∞±a∞）t.Here,xmeasures the distance along the plate from the leading edge.Region I,between the leading edge andx= （u∞-a∞）t,has an Ackeret-type solution with a pressure coefficientCpalong the wall inversely proportional to the well-known Prandtl-Gluert compressibility factor

Region III,betweenx= （u∞+a∞）tand the trailing edge,has a pressure coefficientCpinversely proportional to the Mach number,that is,

Here,the sign ‘+” refers to the lower surface and ‘-” refers to the upper surface.

For a nonlinear case,the essential flow structures are illustrated in Fig.1.We have four basic waves:an oblique shock wave below the plate,a Prandtl-Meyer expansion wave above the plate,an unsteady normal shock wave below the plate,and a rarefaction-type simple wave above the plate.Between these basic waves and the plate,we have four uniform flow regions,denoted as Regions 1,2,3,and 4.The solutions in these uniform regions are given by Bai and Wu,19but for completeness we still outline the detailed expressions below.

(1)Steady oblique shock wave solution(Region 1).The solution in this region is denoted with subscript 1.The classical oblique shock wave theory gives

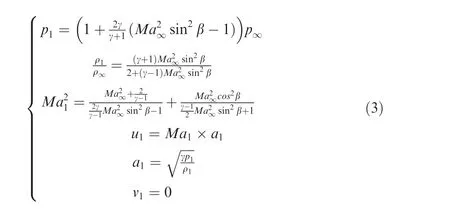
where β is the shock angle determined by

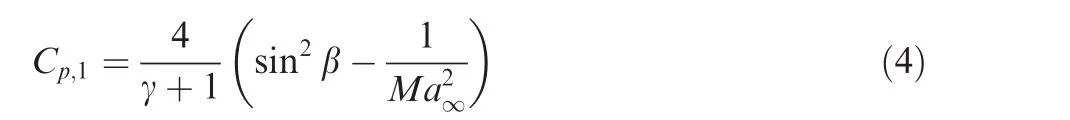
(2)Steady Prandtl-Meyer expansion wave(Region 2).The Mach number Ma2follows the Prandtl-Meyer relation α = ν（Ma2）- ν（Ma∞）with

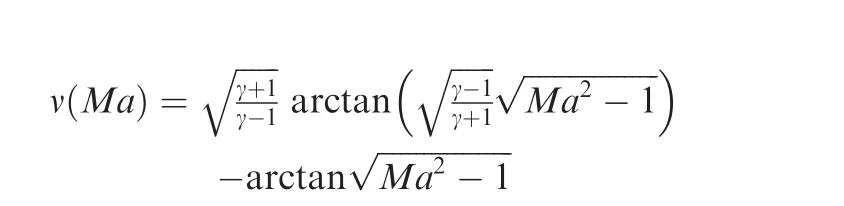
The pressure and density follow the isentropic relations as

(3)Unsteady normal shock wave solution(Region 3).This is a moving shock produced by the vanishing of the vertical component of the velocity v3,and the solution is

(4)Unsteady rarefaction wave(Region 4).This is a rarefaction wave produced with the constraint v4=0,and the solution is

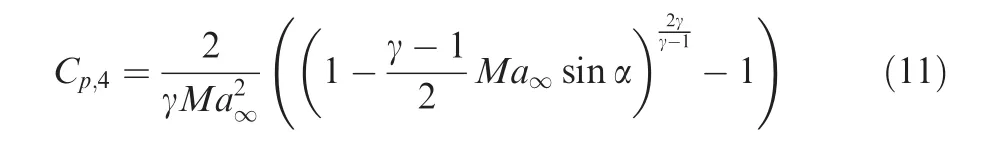
Now consider the characteristic wave speeds in each uniform region.For regioni,withi=1,2,3,4,the characteristic wave speed for the left-going wave is defined by

and the characteristic wave speed for the right-going wave is defined by

3.Shock solution of the non-uniform flow region

For a small angle of attack,Heaslet and Lomax6built a linear theory for the non-uniform region(secondary wave),and this linear solution was connected to the solutions of the uniform regions(basic waves).Bai and Wu19obtained a nonlinear solution for the secondary wave through using the same function form of the linear solution but with the connected uniform region solutions replaced by the corresponding shock wave or expansion wave solutions.This nonlinear solution did not provide any information about the structure of the curved shock wave.Here,we firstly recall these solutions and then build a nonlinear solution for the windward side through establishing a model for the curved shock wave.

3.1.Recall of the modified linear solution

For a small angle of attack,Heaslet and Lomax6built a linear theory for the non-uniform region and obtained

In the nonlinear case,Bai and Wu19put

and rewrote Eq.(15)as

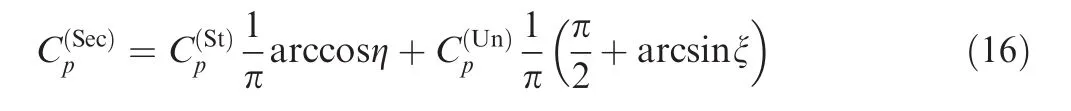
3.2.Self-similar solution of the curved shock wave

As illustrated in Fig.3,the entire shock wave is composed of an oblique shock wave part,a curved shock part,and a straight normal shock wave part.LettingPbe an arbitrary point on the curved shock wave,with the starting and ending points denoted byA（ti）andB（ti）at instantti(i=1,2,3),we now build a self-similar solution of this curved shock wave.

The velocities of the end pointsAandBare

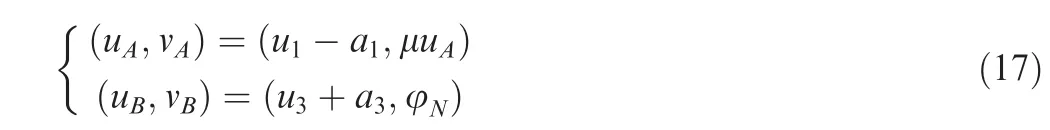
Here,μ is defined by μ =tan（β - α）(with β - α measuring the angle between the oblique shock wave and the wing)and φNis the speed of the normal shock wave.By Eqs.(8)and(7),the explicit expression for the shock speed φNis obtained as

For a self-similar solution,the velocity components （uP,vP）of any pointPof the shock wave satisfyuP=cuxP,vP=cvyPwherecuandcvare constants independent of the positionP.Since （uB,vB）are known,we may write

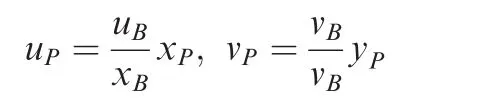
The normal speed φN,Pof the curved shock at pointPwith the unit normal(nPx,nPy)(to be evaluated below)can be estimated as

The pressure in the secondary wave follows the shock relation as

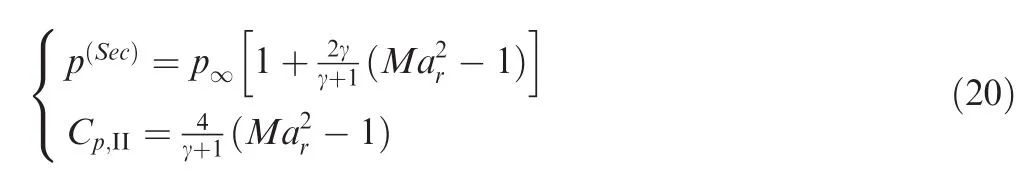
whereMaris the Mach number based onvrwhich is the upstream normal velocity of fluidV∞,n=nPxu∞+nPyv∞relative to the shock speed φN,P,i.e.,Mar=vr/a∞and

Now let us describe a method to evaluate the unit normal nP= ［nPx,nPy］and the shape of the curved shock wave.The positions of pointsAandBare given by （xA,yA）= （uAt,vAt）and （xB,yB）= （uBt,vBt）.The shocks at pointsAandBare assumed to be continuous both for the position and the slope,that is,

Fig.3 Shock wave below plate is composed of three parts:a straight oblique shock wave(OA),a curved shock wave(AB),and a straight normal shock wave(BC).

With these constraints imposed,the curved shock betweenAandBmay be approximated by a cubic curve as

The unit normal of the curved shock is thus nP= ［nPx,nPy］with

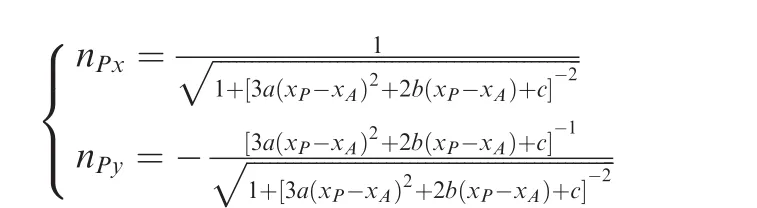
Now,consider two different Mach numbers,Ma∞=5 andMa∞=3,with the same angle of attack α =20o.In Fig.4,we display the shock wave obtained by CFD computation and by the approximate expression of Eq.(21).It is seen that the approximation from Eq.(21)of the shock wave matches reasonably well with the CFD results.

In Fig.5,we display the pressure distributions along the lower surface of the plate.It is seen that the linear theory by Heaslet and Lomax6significantly underestimates the pressure coefficient,while the shock approximation from Eq.(19)gives a pressure comparable to CFD results.

CFD results with other choices of Mach numbers and high angles of attack yield similar conclusions.

4.Normal force behavior

For a linear case,Heaslet and Lomax6provided an explicit expression for lift and showed that during the initial period of time （u∞+a∞）t＜cA,the lift of the plate is constant.Bai and Wu19remarked that even for a nonlinear case,the initial force is almost constant according to CFD results.However,their modified linear model does not predict such a constancy of the initial force.Here,we use similarity assumption and curved shock expression to study the initial force behavior.We also provide the characteristic times at which the force evolution curve changes slope.

4.1.Self-similar solution of the curved shock wave

For the initial period of time

the secondary waves have not yet reached the trailing edge.Firstly,consider the force due to the pressure load on the windward surface.

On the lower surface,the pressure coefficientCp,1in Region 1(0 ＜x＜ （u1-a1）t)is constant,and the pressure coefficientCp,3in Region 3(（u3+a3）t＜x＜cA)is also constant.Hence,the normal force coefficient due to the pressures of these two regions is

Fig.4 Shock waves at several instants.The shock wave by CFD is displayed as contours lines of pressure(these lines are dense near the shock wave).The shock wave by Eq.(21)is displayed as circles.

Fig.5 Comparison between curved shock solution and CFD solution for pressure distribution along lower side of wall.

Under self-similar flow assumption,the pressure coefficient in the secondary waves can be written as

The normal force coefficient due to the secondary wave is

where Ψ,defined by

is independent of time.Hence,the normal force coefficient due to the pressure on the lower surface in total is

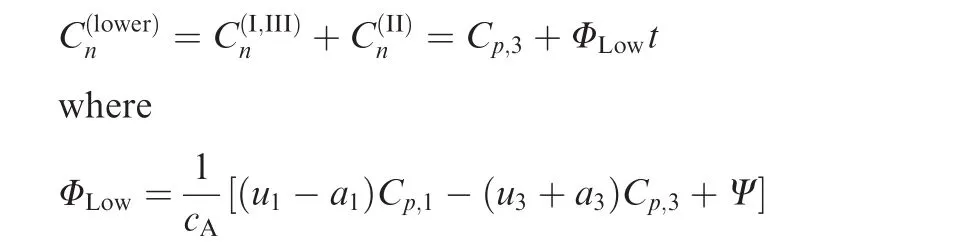
As a result,the normal force coefficient is linear with respect to time for the initial period satisfyingt＜t0,if selfsimilar flow assumption inside the secondary waves is used.

4.2.Slope of the initial force curve

Now we study the magnitude of the slope （ΦLow- Φupp）.This study is useful to understand the near constancy of the initial stage of the force curve observed by numerical simulation.Here,we only consider the force contribution from the lower surface.A similar study for the upper surface should give similar conclusions.

When the Mach number is high enough,the vertical momentum loss across the shock wave may be used to give an approximation of the force due to the lower surface pressure load.This momentum loss is

wherevr=V∞,N-φN,pis the velocity of the inflow stream normal and relative to the shock,and deis a differential element on the shock wave.

The force coefficient due to the momentum loss on the windward side can thus be approximated by

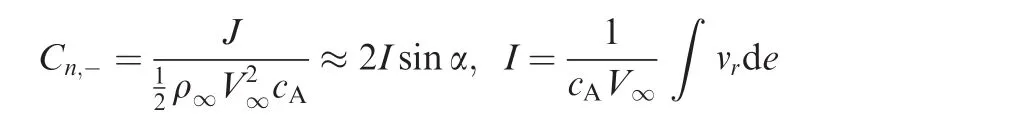
The functionIcan be decomposed asI=I1+I2+I3with

whereA,B,andCare points shown in Fig.3.For the steady oblique shock waveOA,vr=0.For the secondary waveAB,vris given by Eq.(20).For the unsteady normal shock waveBC,vr=V∞,N-φN.Putting these expressions forvrinto Eq.(23),we get

where μ =tan（β - α）.Hence,

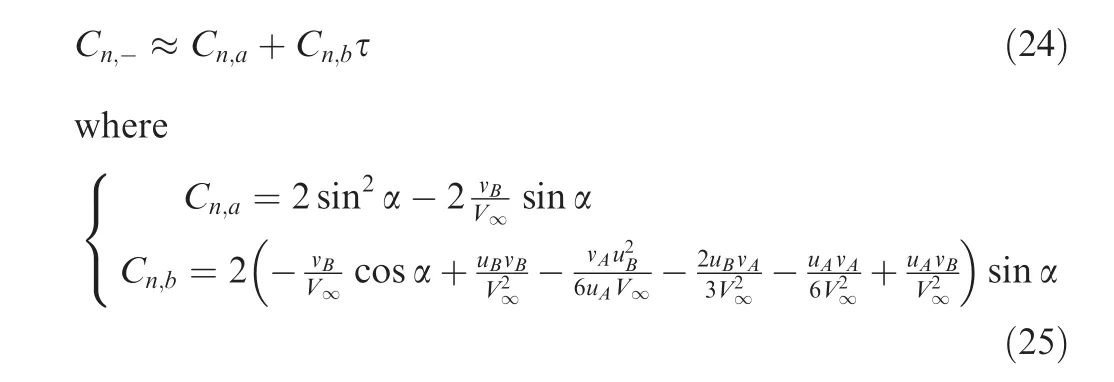
The expressions foruA,vA,uB,andvBare given by Eq.(17).

Table 1 gives the values ofCn,aandCn,bfor several conditions.It is seen that forMa∞large enough,the slopeCn,bis small in comparison withCn,a.

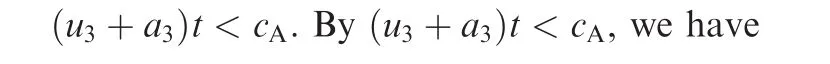
It can be shown thatu3+a3＞u∞+a∞,and thus

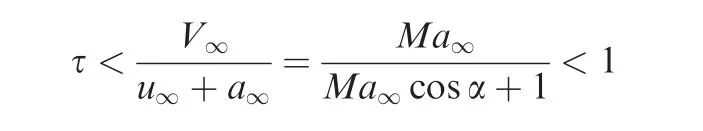
Table 1 Constant part Cn,aand slope Cn,bfor various conditions.

for sufficiently largeMa∞.This means that τ＜ 1 for（u3+a3）t＜cA,so that the small value of the slopeCn,bmakes the force coefficient defined by Eq.(24)almost constant in time before the secondary wave reaches the trailing edge.A similar analysis for the force contribution by waves above the plate would lead to a similar conclusion.In fact,for largeMa∞,the force contribution is dominated by the lower surface compression wave.This may explain the initial force plateau observed in CFD simulations(displayed in Fig.2(b)).

4.3.All time behavior and characteristic times of change of slope

In the linear case,Heaslet and Lomax6proved that the time dependent force curve is composed of a constant segment(equal to the initial value),an arcsine-type curved segment,and another constant segment(steady state value).

In the nonlinear case,Bai and Wu19used CFD computation to show that this curve is composed of a straight segment and various stages of nonlinear parts before a steady-state constant is reached(see Fig.2(b)).The physics of the appearance of various stages has not been discussed.Now let us study the instants characterizing these stages.

The right boundary of the lower secondary wave reaches the trailing edge at

The right boundary of the upper secondary wave reaches the trailing edge at

The left boundary of the upper secondary wave reaches the trailing edge at

The left boundary of the lower secondary wave reaches the trailing edge at

The peak of the upper secondary wave arrives at the trailing edge at τI,which lies between τ2and τ3.The peak of the lower secondary wave arrives at the trailing edge at τJ,which lies between τ1and τ4.Since the inequalities in Eq.(14)hold for any set ofMa∞and α,it can be verified that:τ1＜ τ2＜ τI＜ τJ＜ τ3＜ τ4.

For a specific condition ofMa∞=3 and α =10o,solving Eqs.(3),(5),(7)and(10)gives the velocity and sound speed required in calculating the characteristic wave speeds by Eqs.(12)and(13).Using Eqs.(26)–(29),we get τ1≈ 0.7377,τ2≈ 0.7678,τ3≈ 1.3602,τ4≈ 1.7873.

Fig.6 The force curve for Ma∞ =3 and α =10° obtained by CFD.The theoretical values of the four characteristic times τ1,τ2,τ3,and τ4are marked on the curve.Points τIand τJ correspond to the points of the minimum or maximum local pressure at the trailing edge,respectively.

Fig.6 displays the force curve obtained by CFD and with the four theoretical characteristic times τ1, τ2, τ3,and τ4marked.We observe a clear change of slope at these characteristic times.Note also that the force curve changes slope at τI(due to the arrival of the pressure peak of the upper secondary wave)and τJ(due to the arrival of the pressure peak of the lower secondary wave).

4.4.Viscous effect

In the present study,we have neglected the viscous effect which should develop a boundary layer along the wall.At a high Mach number,the boundary layer may become thick due to aerodynamic heating.This thick boundary layer has interaction with the shock wave,a phenomenon known as viscous interaction.A simple treatment within the context of the simple model would be adding a displacement thickness to the wall which in turn modifies the effective angle of attack in application of a viscous model.In case that the Reynolds number is large and that there is no flow separation,such an effect should be small.

whereReis the Reynolds number.The force variation is accomplished within τ=O（1）for the present application.Thus,with a Reynolds number typically of the order of 106or higher,δ is of the order of 10-3cA,so the effect of viscosity may be considered to have no essential importance.If flow details should be considered,for instance in the leeward side,the problem taking viscosity into account defines a viscous rarefaction wave problem for which a solution is very difficult.21

5.Conclusions

This paper has studied the flow structure of a secondary shock wave resulting from an interaction between steady and unsteady shock waves for a flat plate attaining suddenly an angle of attack in supersonic flow.A self-similar solution is obtained for the curved shock wave.Using self-similar assumption,it is proven that the initial period of the force variation curve is linear with respect to time with a very small slope.This explains the numerical observation that the force is almost constant in time at the initial stage.The subsequent arrivals of the edges and peaks of the two secondary waves give six characteristic times at which the force curve changes slope.This conclusion matches very well with numerical computation by CFD.

In this paper,we only considered an inviscid flow model.Viscosity shall have some influence.For instance,the unsteady waves in a linear case have been previously given by the inviscid piston theory.15–17Recently,the piston theory has been developed taking into account viscous effect correction.22More recently,the flow parameters in the uniform flow regions separated by secondary waves have viewed as an initial discontinuity to develop a Riemann solution,and it has been found that the secondary wave on the leeward side is bounded by a left-going shock wave.23

Acknowledgements

The authors thank the reviewers and editors for their valuable comments to improve the manuscript.This work was supported by the Double First-Rate Project of Tsinghua University(2017)(No.11472157)and partly by the National Basic Research Program of China(No.2012CB720205).

1.Phillips WF.Mechanics of flight.Hoboken:John Wiley&Sons;2004.

2.Hernandes F,Soviero PAO.A numerical model for thin airfoils in unsteady compressible arbitrary motion.J Brazilian Soc Mech Sci2007;29(3):253–61.

3.Bisplinghoff RL,Ashley H,Halfman RL.Aeroelasticity.New York:Dover;1996.

4.Biot MA.Loads on a supersonic wing striking a sharp-edged gust.J Aeronaut Sci1949;16(5):296–300.

5.Mastroddi F,Stella F,Cantiani D,Vetrano F.Linearized aeroelastic gust response analysis of a launch vehicle.J Spacecraft Rockets2011;48(3):420–32.

6.Heaslet MA,Lomax H.Two-dimensional unsteady lift problems in supersonic flight.Washington,D.C.:NASA;1949.Report No.:NACA TN-1621.

7.Bai CY,Li J,Wu ZN.Unsteady lift for impulsively started transonic/supersonic flow.ASME international mechanical engineering congress2015.New York:ASME;2015.

8.Wu ZN,Bai CY,Xu SS,Li J,Lin J,Chen ZJ,et al.Impulsively starting flow problem:from incompressible to hypersonic flow.Acta Aeronaut Astronaut Sin2015;36(8):2578–90[Chinese].

9.Lomax H,Heaslet MA,Fuller FB,Sluder L.Two-and threedimensional unsteady lift problems in high-speed flight.Washington,D.C.:NASA;1952.Report No.:NACA Report 1077.

10.Leishman JG.Validation of approximate indicial aerodynamic functions for two-dimensional subsonic flow.J Aircraft1988;25(10):914–22.

11.Leishman JG.Unsteady lift of a flapped airfoil by indicial concepts.J Aircraft1994;31(2):288–97.

12.Nagarajan H,Leishman JG.Unsteady aerodynamics of a flapped airfoil in subsonic flow by indicial concepts.J Aircraft1996;33(5):855–68.

13.Sitaraman J,Baeder JD.Computational-fluid-dynamics-based enhanced indicial aerodynamic models.JAircraft2004;41(4):798–811.

14.Jaworski JW,Dowell EH.Supersonic indicial lift functions from transform methods.AIAA J2007;45(8):2106–11.

15.Ashley H,Zartarian G.Piston theory-a new aerodynamic tool for the aeroelastician.J Aeronaut Sci1956;23(12):1109–18.

16.Liu DD.From piston theory to a unified hypersonic-supersonic lifting surface method.J Aircraft1997;34(3):304–14.

17.Dowell EH,Bliss DB.New look at unsteady supersonic potential flow aerodynamics and piston theory.AIAA J2013;51(9):2278–81.

18.Bai CY,Wu ZN.Hypersonic starting flow at high angle of attack.Chin J Aeronaut2016;29(2):297–304.

19.Bai CY,Wu ZN.Supersonic indicial response with nonlinear corrections by shock and rarefaction waves.AIAA J2017;55(3):883–93.

20.Shivamoggi BK.Theoretical fluid dynamics.New York:John Wiley&Sons;1997.

21.Matsumura A,Nishihara K.Asymptotics toward the rarefaction waves of the solutions of a one-dimensional model system for compressible viscous gas.Jpn J Appl Math1986;3(1):1–13.

22.Liu W,Zhang CA,Han HQ,Wang FM.Local piston theory with viscous correction and its application.AIAA J2017;55(3):942–54.

23.Bai CY,Wu ZN.Hybrid Riemann-self-similar flow structure by steady and unsteady wave interaction.AIAA J2017.https://doi.org/10.2514/1.J055995.