Modeling and control for cooperative transport of a slung fluid container using quadrotors

Hassan SAYYAADI,Ali SOLTANI

School of Mechanical Engineering,Sharif University of Technology,Tehran 11155-9567,Iran

1.Introduction

Control of partially filled liquid containers on desired trajectories under effect of liquid sloshing has aroused interest of many researchers.For example in study,1a general framework to control space manipulators with complex payloads such as payloads with sloshing fluid has been introduced.In another study,2two methods for controlling surface of liquid in an open container carried by a robot arm have been proposed by considering fundamental mode of liquid oscillation.An infinite impulse response filter to alter the acceleration profile and tilting the container parallel to the beginning and ending wave are the implemented methods to control the liquid surface properly,which have been examined experimentally.Furthermore,in another research,3a reduced 7th order robustH∞controller has been designed to control launch vehicle with sloshing fuel in presence of disturbances,structured and unstructured parameter uncertainties.In order to construct a high speed transfer system for a liquid container that satisfies the reduction of endpoint residual vibration and has robustness against changes in the static liquid level,a suitable nominal model has been adopted and an appropriate reference trajectory has been determined by the optimization in another research.4Based on the command inputs and using the suitable nominal model,anH∞feedback control system has been applied to this process,and its effectiveness has been shown through simulations and experiments.Furthermore,an active control method that takes into account the rotational and translational motion of the container has been presented,which can achieve complete suppression of sloshing during the whole transfer process.Moreover,to suppress sloshing in the container during acceleration and deceleration along an inclined transfer path,authors in the study5have presented a method to actively control the container’s rotational motion.The effectiveness of the proposed method has been demonstrated through simulations and experiments.Also,research6presents a trajectory control design method to suppress residual vibration in transfer systems without the need to directly measure vibration which needs a large number of complicated sensors.The proposed method consists of two parts.First part is about shaping frequency characteristics of the controller to suppress the vibration.In the second part,various parameters of the control elements are determined by solving an optimization problem with penalty terms expressed by the constraints of both of the time and frequency domains.The effectiveness of the control design method is shown by experiments.Furthermore,in another study7and in a similar work,8a method is proposed for the design of a switching surface in presence of mismatched uncertainties.Also,a design method for a sliding mode observer based on high gain is proposed in this paper to reconstruct the states of the system for implementation of the sliding mode control.The proposed method is implemented for slosh-free motion of a container in simulations and experiments.In another research,9authors have studied modeling and control problem for planar maneuvering of space vehicles with fuel slosh dynamics.A multi-mass–spring model is considered for characterization of the most prominent sloshing modes.Moreover,a Lyapunov-based nonlinear feedback control law has been designed to achieve the control objective which has been examined in simulations.In another work,the authors have investigated the point-to-point liquid container transfer control problem for a robot with two prismatic and one revolute joints.10In continuation of their research,11they proposed a solution for thrust vector control problem for an upper-stage rocket with fuel slosh dynamics.In both of these studies,10,11performance of the proposed control laws has been examined by simulations.In a recent work,12authors have presented two methods to reduce an infinite number of sloshing modes in a moving liquid container.The first method is command smoothing to eliminate slosh by using the first mode frequency,while the second one is a combined input shaping and command-smoothing architecture.The input shaper reduces slosh for the first mode and the command smoother suppresses slosh for the third and higher modes.Experiments have validated the simulated dynamic behavior and the effectiveness of the methods.

Unmanned Aerial Vehicles(UAVs)are implemented in various operations such as search and rescue operations,military missions and urban operations.13In these missions,it may be necessary that UAVs carry a payload.Load transport may be performed by a single quadrotor14–31or by a team of UAVs.32–37In some of these studies,load is gripped by UAVs.28,32,37However,in most of the studies about load transport by aerial robots,the load is suspended from UAVs.14–27,29–31,33–36If the load is cable suspended,the system of equations of motion will be hybrid because the cables can be slack or taut during the motion.Therefore,dynamics of the system will be switching.Hybrid nature of slung load systems has been investigated in some studies.29,38Moreover,cable suspended load and UAV system can be considered as ann-link robotic manipulator with flexible links.Interesting researches about such robots can be found in the literature.39–41In the following,some of the studies about slung load transport by UAVs are described in more detail.For instance,dynamic modeling and control of a helicopter with a slung load has been investigated in work.23Authors have modeled behavior of representative trim variable values(i.e.cable angle and longitudinal and lateral cyclic blade pitch angles)and modes(i.e.flight dynamics and load modes)due to changes of some model parameters(e.g.cable length,load mass,and equivalent flat plate area).Moreover,they have designed variance constrained controllers for the system.Most of the works about suspended load control by quadrotors have been reported by GRASP laboratory.For example,in study,32control laws for grasping and transporting a payload on threedimensional trajectories by a team of quadrotors have been presented and tested in experiments appropriately.Also,in another study,29trajectory generation and control of a quadrotor with a cable suspended point-mass load especially in planar transports have been studied,and proposed controllers were examined experimentally.In the work,18authors have extended their geometric control laws for threedimensional transport.In a research about aerial transport of slung payloads,33feasible trajectories for cooperative transport of cable suspended payloads(rigid bodies or pointmasses)from quadrotors have been generated by demonstrating that system is a hybrid differentially flat system.Authors in their another paper34have designed a controller for quadrotors to transport a cable suspended mass-point load on a desired trajectory while maintaining a relative formation.Also,a similar research36has been reported for rigid body load case when number of quadrotors are more than or equal to six.In a more restricted mission,35proper control law has been proposed for trajectory control of a cable suspended rigid body load by a team of quadrotors when number of members is more than or equal to three.

In all of the mentioned aerial transport researches,the payload is considered as a rigid body or mass-point,and its inert properties are assumed to be constant.However,if the payload contains sloshing fluid,this assumption will not be correct and the proposed control laws lose their effectiveness in precise trajectory tracking surely.For instance,by proposing a nonlinear model for dynamic behavior of tank vehicles with sloshing fluid in the study,42it has been demonstrated that tank vehicle may be unstable under certain operations and road conditions.

Therefore,modeling and control problem for planar aerial transport missions of a sloshing fluid container suspended from a team of quadrotors via massless links are studied in the present study.In spite of the existing studies in the literature,controllers are designed in the present study,so that quadrotors can stabilize the slung container at a desired pose and suppress sloshing modes of the liquid simultaneously.To consider fluid sloshing in dynamic modeling of the system,sloshing modes are modeled by multi spring-mass systems.The proposed control scheme consists of a load pose and fluid sloshing controller,controllers of the links directions and attitude controllers of the quadrotors.Controller of the load pose and fluid sloshing together with the controller of the links directions determine thrust forces and desired attitudes of the quadrotors.Then,each quadrotor uses its attitude controller to track its desired attitude.This paper is organized as follows:

In dynamic modeling section,equations of motion of the considered system are formulated by Euler-Lagrange method.In the next section,control laws are proposed.Moreover,Lyapunov stability theorem along with a theorem of singularly perturbed systems is implemented to prove stability of the closed loop system of tracking errors in appendices.In simulation section,stabilizing mission of a container suspended from three quadrotors via three massless rigid links is organized to verify performance of the designed controllers.To have more accurate verification,initial conditions and properties of container and fluid are brought from the literature.Furthermore,capabilities of the proposed control law are compared with the existing results in the literature.Finally,summary of the paper is presented briefly.

Fig.1 Multi-mass-spring model of liquid sloshing and container suspended from quadrotors via massless rigid links.

2.Dynamic modeling

This section formulates dynamics of a team ofnquadrotors moving a liquid filled container via rigid massless links in a vertical plane including prominent liquid sloshing modes.

Remark 1.Actually,links cannot be completely rigid and massless in practice.However,if mass of the links is small enough,their inertial effects on dynamics of the system can be neglected.Therefore,links are assumed to be massless in many studies such as researches35,36similarly.Furthermore,if magnitudes of forces and torques acting on a link are small in comparison with its stiffness,rigidity assumption will be reasonable.This assumption has been made in studies35,36too.

Centers of masses of the quadrotors and container and attachment points of the rigid links are supposed to be in the same vertical plane as shown in Fig.1,θ represents angle between positive directions ofy-axes of body fixed and inertial frames,φirepresents angle betweenith link and positive direction ofy-axis of inertial frame and qQirepresents unit vector along thrust ofith quadrotor.Therefore,quadrotors should not perform any yaw or pitch motion at all.In other words,yaw and pitch angles of the quadrotors should be controlled at zero.Furthermore,the links have been pivoted to the container and center of mass of the quadrotors.Therefore,links do not affect rotational motion of the quadrotors.Mass and rolling moment of inertia for each quadrotor are denoted bymQiandJQirespectively whilemcandIcrepresent container mass and moment of inertia aboutxaxis of its body fixed frame respectively.In particular,sloshing liquid is modeled as a multi-mass-spring system where oscillation frequencies of mass-spring elements representmmodes of sloshing.Therefore,fluid is modeled by moment of inertiaI0assigned to a rigidly attached massm0and point massesmi,i=1,2,...,m,whose relative positions along container-fixed lateral axis are denoted bysi.Each sloshing mode is modeled via restoring force-kisi(kirepresents stiffness ofith sloshing mode equivalent spring)which acts on the massmiwhenever the mass is displaced from its neutral positionsi=0.For simplicity,it is assumed that the center of mass of the container is at the same location as the center of mass of the undisturbed liquid.Vertical locations of liquid masses in the container fixed frame denoted byh0andhiare represented with respect to the center of mass of undisturbed liquid.The parametersm0,mi,I0,h0,hi,kidepend on the shape of the container,the characteristics of the liquid,and the fill ratio of the container.

Moreover,to preserve the static properties of the liquid,the sum of all the masses must be the same as the fluid massmf,and the center of mass of the model must be at the same elevation as that of the liquid,i.e.

As demonstrated in Fig.1,^j and^k are transverse and cylindrical axes of the container fixed frame respectively.In the following,position vector of the container center of mass in inertial frame is denoted by rcwhile airepresents position vector of the attachment point of theith link in the body fixed frame of the container.Moreover,lidenotes length of theith link.Furthermore,rotation matrix of inertial frame to the body fixed frame of the container Rcand unit vector along theith link qpiare determined by

Definitions of θ and φiare obvious from Fig.1.Consequently,position of the masses of the system in inertial frame can be found from the following equations:

in which rQirepresents position vector ofith quadrotor center of mass in inertial frame,rmirepresents position vector of equivalent mass forith sloshing mode in inertial frame and rm0represents position vector of static fluid center of mass in inertial frame.

Therefore,kinetic energies of each quadrotorTQi,fluidTfand containerTccan be computed as

in whichzciszcoordinate of container center of mass in inertial frame,zQiiszcoordinate ofith quadrotor center of mass in inertial frame,gis gravity acceleration.

Now,LagrangianLsyscan be defined as

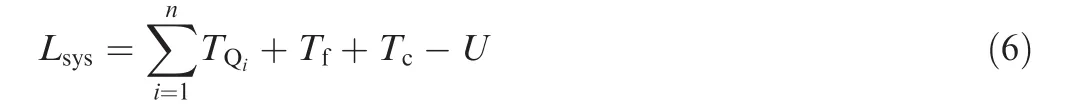
Applying Lagrange’s formulation with dissipation and input forces and torques,equations of motion can be obtained as

Fig.2 Thrust forces and rolling torques.

In Eq.(7),matrix M（χ）can be represented as

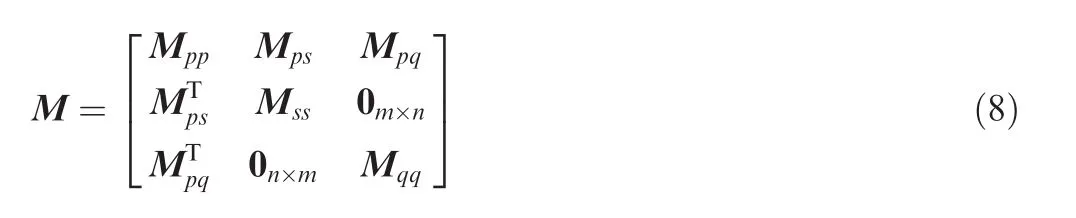
in which matrices Mpp,Mps,Mpq,Mssand Mqqare defined by the following equations:

in which D（·）represents diagonal matrix of a vector.

in which l represents vector of lengths of links.

where

in which qpiis unit vector alongithlink.

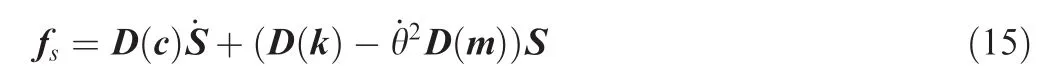
in which c,k and m represent vector of damping coefficients of sloshing modes,stiffness of sloshing mode equivalent spring and equivalent mass of sloshing.

Moreover,matrix E in equations of motion(7)is determined by

Also,vector u in Eq.(7)is composed by thrust force vectors of quadrotors as the following equation:

in whichuiis net thrust force of theith quadrotor while qQiis unit vector of its direction.

3.Control design

In this section,proper control laws are designed so that quadrotors stabilize the container at a desired pose and suppress the fluid sloshing.Also,relative directions of the links with respect to the container should be stabilized at a desired attitude.

Tracking error of the container pose e is defined as

in which pdis desired pose of container.

Also,tracking errors for angles of the links are defined by

in whicheφirepresentsith link angle error.

in which the superscript d means desired.

3.1.Controller structure

Controller of the system is a hierarchical controller composed of container pose and sloshing controller,links’directions controller and quadrotors’attitude controllers.Container pose and sloshing controller together with links’directions controller determines thrust forces of the quadrotors and desired directions of the thrust forces of the quadrotors.On the other hand,quadrotors track the desired attitude by implementing their attitude controllers.

3.2.Quadrotor attitude tracking controller design

In this section,attitude controller of the quadrotor is proposed so that origin of the closed loop system of quadrotor attitude tracking error will be almost global exponential attractive.

Proposition 1.(Stability of Quadrotor Attitude Controlled Flight Mode).We consider rolling moment of each quadrotor which is defined as

for any positive constantKΩ,Kqand 0＜ ε＜ 1.And we suppose that initial conditions satisfy the following inequalities:

Proof.See Appendix A.□

Remark 3.Actually,Eqs.(23)and(24)define region of attraction for the origin of the closed loop system of attitude tracking error.Importance of the required initial conditions is described in Appendix A.One should note that these conditions are not too restrictive,because initial condition(23)only imposes that angle between desired direction of the thrust and its initial value should be less than 180°.Furthermore,region of attraction defined by Eq.(24)can be extended by increasingKqor decreasing ε.Therefore,origin of closed loop system of attitude tracking error is almost global exponential attractive.

3.3.Controller design for container pose,sloshing and links’directions

To control pose of container,fluid sloshing and directions of the links,thrust force and desired attitude of each quadrotor are adopted as

where B†is Pseudo inverse of matrix B which is defined as

Remark 4.Pseudo inverse of matrix B exists if rank of matrix is three.Necessary condition for this is that number of quadrotors is more than or equal to threen≥3.To ensure that matrix rank remains equal to three,it is sufficient that rank of matrix is initially 3 and relative directions of the links with respect to the container frame are stabilized at their initial orientation.

Remark 5.Maximum number of the quadrotors are not limited theoretically.However,systems with numerous quadrotors need high speed processors to calculate Pseudo inverse to determine udpin real time.Furthermore,maximum number of quadrotors is limited by the bandwidth of the communications.

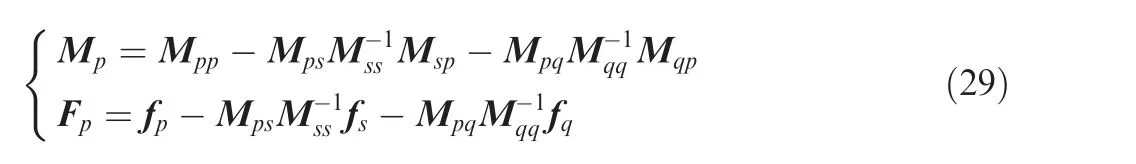
In Eq.(27),matrix Mpand vector Fpare determined by

Furthermore,vector v in Eq.(27)is computed via

in which γiare positive real constants and matrices H and Y are defined as

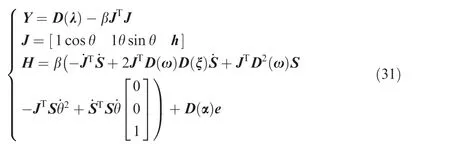
in whichKφandK˙φare positive real constants,eφand˙eφare vector of errors of links’angles and first derivative of eφwith respect to time.

Proposition 2.(Stability of container pose,liquid sloshing and links’directions tracking errors).By adaption of magnitudes and desired directions for thrust forces as Eq.(25),ε*can be found such that for all ε＜ ε*,zero equilibrium point of tracking errors of links directions（eφ,˙eφ）=（0,0）will be exponentially stable while（e,˙e,S,˙S）=（0,0,0,0）will be an asymptotically stable equilibrium point for closed loop system of tracking errors of container pose and sloshing modes.

Proof.See Appendix B.□

4.Simulation

In this section,designed feedback control laws are examined in stabilizing a container by three identical quadrotors considering only two modes of sloshing.To verify the performance of the proposed control laws,initial conditions and physical properties of container and sloshing liquid are adopted from Ref.10as

Values of the control parameters α,λ,β and γ are the same as values selected in Ref.10for them:

Fig.3 Time response of container pose.

wherea=1 m is radius of the container andb=2 m is height of the container edge from its center of mass.Physical properties of the quadrotors are imported from Ref.43to the simulation as

Considering conditions introduced by Eqs.(23)and(24),initial conditions for directions of thrust vectors of the quadrotors are set as

Fig.4 Time response of s1and s2.

Fig.5 Time response of links’directions relative to container.

Fig.6 Time response of attitude error functions of quadrotors ηi,i=1,2,3.

Fig.7 Thrust forces of quadrotors.

Control parameters for the links’directions and quadrotor attitudes are chosen as

Fig.8 Rolling torques of quadrotors.

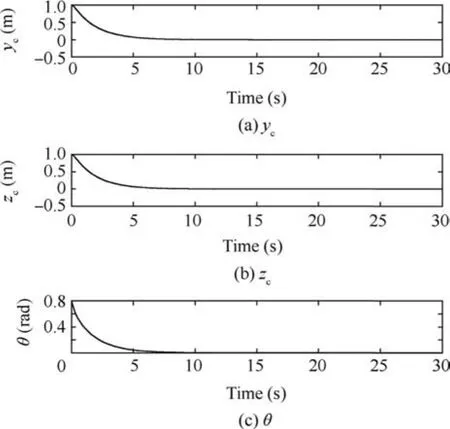
Fig.9 Time response of container pose by controller proposed in Ref.36

Fig.10 Time response of s1and s2pose by controller proposed in Ref.36

To compare capabilities of the proposed control law with the existing slung load transport controllers in the literature,the load stabilization mission is simulated by the controller proposed in Ref.36,As depicted in Figs.9 and 10,although attitude and position of the container are stabilized by the controller,liquid sloshing is not controlled at all.In the other words,the proposed controller in the present study can control the load position,attitude and fluid sloshing simultaneously while the controller proposed in Ref.36controls only the position and attitude of the load.

5.Conclusions

In this study,aerial transport problem of a liquid filled container suspended via rigid massless links from quadrotors has been investigated.Feedback control laws have been introduced so that quadrotors can stabilize container at the desired pose and eliminate liquid sloshing.Also,feedback control laws enable quadrotor to control links’directions relative to the tank.Stability of zero point for closed loop system of tracking errors has been established by Lyapunov stability theorem along with an argument about singularly perturbed systems.Moreover,effectiveness of the designed control laws has been examined in simulation.Moreover,superiority of the proposed control laws over an existing slung load controller is demonstrated in simulations.Experimental verification of the proposed control laws may be challenging due to measurements of sloshing states needed for feedback,which can be solved by designing a proper observer.Also,designing controllers which are robust against parametric uncertainties and disturbances may be included in future works.

Appendix A

Therefore,a Lyapunov function is introduced as

Appendix B

Consequently,point（eφ,˙eφ）=（0,0）is an exponentially stable equilibrium point for the closed loop system presented by Eq.(B2).

According to the equations of motion of system,one can find that

Then,dynamics of the container pose can be presented by

Definition of Mp,Fpand B can be found from Eqs.(29)and(28)respectively.As described formerly,in the slow model up≡udpand so from Eq.(27),it can be concluded that

A Lyapunov functionVcan be candidate as in which it is assumed that

Then,Vwill be positive definite.For example,consider two modes of sloshing and λ1= λ2= λ3= λ,and then sufficient conditions for satisfying Eq.(B7)are

Time derivative ofVusing the equations of motion for the slow system and the feedback control law will be

which satisfies˙V≤0.Using LaSalle’s principle,45it is easy to prove asymptotic stability of the origin of the closed loop system defined by Eq.(B5)and the proposed feedback control law(30).Using theorem 11.2 of Ref.45,there exist ε*such that for all 0＜ ε＜ ε*,differences between states of full model and slow model are all in order ofO（ε）uniformly. □

1.Carton P,Chre´tien JP,Maurette M.Simulation and control of space manipulators bearing complex payloads.IFAC ProcVolumes1989;22(7):127–32.

2.Feddema JT,Dohrmann CR,Parker GG,Robinett RD,Romero DJ,Schmitt DJ.Control for slosh-free motion of an open container.IEEE Cont Syst1997;17(1):29–36.

3.Xing GQ,Bainum PM,Li F.Design of a reduced order H∞robust controller for an expendable launch vehicle in the presence of structured and unstructured parameter uncertainty1.Acta Astronaut1997;41(2):121–30.

4.Yano K,Terashima K.Robust liquid container transfer control for complete sloshing suppression.IEEE Trans Cont Syst Technol2001;9(3):483–93.

5.Yano Ki,Higashikawa S,Terashima K.Motion control of liquid container considering an inclined transfer path.Cont Eng Pract2002;10(4):465–72.

6.Yano K,Terashima K.Sloshing suppression control of liquid transfer systems considering a 3-D transfer path.IEEE/ASME Trans Mechatron2005;10(1):8–16.

7.Bandyopadhyay B,Gandhi PS,Kurode S.Sliding mode observer based sliding mode controller for slosh-free motion through PID scheme.IEEE Trans Ind Electron2009;56(9):3432–42.

8.Kurode S,Spurgeon SK,Bandyopadhyay B,Gandhi PS.Sliding mode control for slosh-free motion using a nonlinear sliding surface.IEEE/ASME Trans Mechatron2013;18(2):714–24.

9.Reyhanoglu M,Rubio HJ.Nonlinear dynamics and control of space vehicles with multiple fuel slosh modes.Cont Eng Pract2012;20(9):912–8.

10.Reyhanoglu M,Rubio HJ.Nonlinear modeling and control of slosh in liquid container transfer via a PPR robot.Commun Nonlinear Sci Numer Simul2013;18(6):1481–90.

11.Rubio HJ,Reyhanoglu M.Thrust-vector control of a three-axis stabilized upper-stage rocket with fuel slosh dynamics.Acta Astronaut2014;98:120–7.

12.Zang Q,Huang J,Liang Z.Slosh suppression for in finite modes in a moving liquid container.IEEE/ASME Trans Mechatron2015;20(1):217–25.

13.Lindsey Q,Mellinger D,Kumar V.Construction with quadrotor teams.Auton Robot2012;33(3):323–36.

14.Dai S,Lee T,Bernstein DS.Adaptive control of a quadrotor UAV transporting a cable-suspended load with unknown mass.53rd IEEE Conference on Decision and Control;2014 Dec 15–17;Los Angeles,USA.Piscataway:IEEE Press;2015.p.6149–54.

15.Faust A,Palunko I,Cruz P,Fierro R,Tapia L.Automated aerial suspended cargo delivery through reinforcement learning.Artif Intell2014;247:381–98.

16.Cruz P,Fierro R.Autonomous lift of a cable-suspended load by an unmanned aerial robot.2014 IEEE Conference on Control Applications(CCA);2014 Oct 8–10;Juan Les Antibes,France.Piscataway:IEEE Press;2014.p.802–7.

17.Fusato D,Guglieri G,Celi R.Flight dynamics of an articulated rotor helicopter with an external slung load.J Am Helicopter Soc2001;46(1):3–13.

18.Sreenath K,Lee T,Kumar V.Geometric control and differential flatness of a quadrotor UAV with a cablesuspended load.52nd IEEE Conference on Decision and Control;2013 Oct 10–13;Firenze,Italy;Piscataway:IEEE Press;2013.p.2269–74.

19.Goodarzi FA,Lee D,Lee T.Geometric control of a quadrotor UAV transporting a payload connected via flexible cable.Int J Cont Autom Syst2015;13(6):1486–98.

20.Goodarzi FA,Lee D,Lee T.Geometric stabilization of a quadrotor UAV with a payload connected by flexible cable.2014 American Control Conference;2014 June 4–6;Portland,USA;Piscataway:IEEE Press;2014.p.4925–30.

21.Faust A,Palunko I,Cruz P,Fierro R,Tapia L.Learning swingfree trajectories for UAVs with a suspended load.2013 IEEE International Conference on Robotics and Automation;2013 May 6–10;Karlsruhe,Germany;Piscataway:IEEE Press;2013.p.4902–9.

22.Tang S,Kumar V.Mixed integer quadratic program trajectory generation for a quadrotor with a cable-suspended payload.2015 IEEE International Conference on Robotics and Automation(ICRA);2015 May 26–30;Seattle,USA;Piscataway:IEEE Press;2013.p.2216–22.

23.Oktay T,Sultan C.Modeling and control of a helicopter slungload system.Aerosp Sci Technol2013;29(1):206–22.

24.Feng Y,Rabbath CA,Su CY.Modeling of a micro UAV with slung payload.In:Valavanis KP,Vachtsevanos GJ,editors.Handbook of unmanned aerial vehicles.Dordrecht:Springer,Netherlands;2015.p.1257–72.

25.Notter S,Heckmann A,McFadyen A,Gonzalez F.Modelling,simulation and flight test of a model predictive controlled multirotor with heavy slung load.IFAC-PapersOnLine2016;49(17):182–7.

26.Potter JJ,Adams CJ,Singhose W.A planar experimental remotecontrolled helicopter with a suspended load.IEEE/ASME Trans Mechatron2015;20(5):2496–503.

27.Palunko I,Faust A,Cruz P,Tapia L,Fierro R.A reinforcement learning approach towards autonomous suspended load manipulation using aerial robots.2013 IEEE International Conference on Robotics and Automation;2013 May 6–10;Karlsruhe,Germany;Piscataway:IEEE Press;2013.p.4896–901.

28.Pounds PEI,Bersak DR,Dollar AM.Stability of small-scale UAV helicopters and quadrotors with added payload mass under PID control.Auton Robot2012;33(1):129–42.

29.Sreenath K,Michael N,Kumar V.Trajectory generation and control of a quadrotor with a cable-suspended load-A differentially- flat hybrid system.2013 IEEE International Conference on Robotics and Automation;2013 May 6–10;Karlsruhe,Germany;Piscataway:IEEE Press;2013.p.4888–95.

30.Palunko I,Fierro R,Cruz P.Trajectory generation for swing-free maneuvers of a quadrotor with suspended payload:A dynamic programming approach.2012 IEEE International Conference on Robotics and Automation;2012 May 14–18;Saint Paul,USA;Piscataway:IEEE Press;2012.p.2691–7.

31.Bisgaard M,la Cour-Harbo A,Johnson EN,Bendtsen JD.Vision aided state estimator for helicopter slung load system.IFAC Proc2007;40(7):425–30.

32.Mellinger D,Shomin M,Michael N,Kumar V.Cooperative grasping and transport using multiple quadrotors.In:Martinoli A,Mondada F,Correll N,Mermoud G,Egerstedt M,Hsieh MA,et al.,editors.Distributed autonomous robotic systems:The 10th international symposium.Heidelberg:Springer,Berlin Heidelberg;2013.p.545–58.

33.Kumar V,Sreenath K.Dynamics,control and planning for cooperative manipulation of payloads suspended by cables from multiple quadrotor robots.Robot:Sci Syst2013;1–8.

34.Lee T,Sreenath K,Kumar V.Geometric control of cooperating multiple quadrotor UAVs with a suspended payload.52nd IEEE Conference on Decision and Control;2013 Oct 10–13;Firenze,Italy;Piscataway:IEEE Press;2013.p.5510–5.

35.Lee T.Geometric control of multiple quadrotor UAVs transporting a cable-suspended rigid body.53rd IEEE Conference on Decision and Control;2014 Dec 15–17;Los Angeles,USA;Piscataway:IEEE Press;2015.p.6155–60.

36.Wu G,Sreenath K.Geometric control of multiple quadrotors transporting a rigid-body load.53rd IEEE Conference on Decision and Control;2014 Dec 15–17;Los Angeles,USA;Piscataway:IEEE Press;2015.p.6141–8.

37.Parra-Vega V,Sanchez A,Izaguirre C,Garcia O,Ruiz-Sanchez F.Toward aerial grasping and manipulation with multiple UAVs.J Intell Robot Syst2013;70(1):575–93.

38.He W,Ge SS.Cooperative control of a nonuniform gantry crane with constrained tension.Autom2016;66:146–54.

39.He W,Chen Y,Yin Z.Adaptive neural network control of an uncertain robot with full-state constraints.IEEE Trans Cybern2016;46(3):620–9.

40.He W,Dong Y,Sun C.Adaptive neural impedance control of a robotic manipulator with input saturation.IEEE Trans Syst Man Cybern:Syst2016;46(3):334–44.

41.He W,Ouyang Y,Hong J.Vibration control of a flexible robotic manipulator in the presence of input deadzone.IEEE Trans Ind Inform2017;13(1):48–59.

42.Dai L,Xu L,Setiawan B.A new non-linear approach to analysing the dynamic behaviour of tank vehicles subjected to liquid sloshing.Mech Eng,Part K;J Multi-body Dyn2005;219(1):75–86.

43.Bouabdallah S.Design and control of quadrotors with application to autonomous flying[dissertion].Lausanne:EPfL University;2007.

44.Bullo F,Lewis AD.Geometric control of mechanical systems.New York-Heidelberg-Berlin:Springer-Verlag;2004.

45.Khalil HK.Nonlinear systems.New Jersey:Prentice Hall;2002.