翼板刚度与埋深对加翼桩水平承载性能影响分析

陈灿明，何建新，王曦鹏，苏晓栋，黄卫兰

作为海上风电基础的钢管桩为了承受巨大的风、浪、流等水平荷载，其直径越来越大，施工难度也显著增加［1－2］。加翼桩作为大直径单桩基础的改进型式，通过设置翼板，在保证桩基水平承载力的基础上减小基桩桩径，从而降低施工难度和节约成本，进一步推动海上风电的发展。2016年南京水利科学研究院设立了中央级公益性科研院所基本科研业务费专项资金项目《用于提高水平承载能力的加翼桩研究》，研究加翼桩翼板面积、形状、刚度、埋深等因素对加翼桩水平承载力的影响，为新型结构的工程应用提供技术支撑。本文主要介绍翼板刚度和埋深对加翼桩水平承载性能影响的计算分析结果［3－4］。

1 计算模型与相关参数

以江苏某海上风电场大直径单桩基础为计算模型，大直径钢管桩桩长73．0 m，入土深度55．0 m，桩径5．0 m，壁厚0．08 m。加翼桩采用一桩四翼对称布置，翼板材质和厚度与桩体相同，规定翼板长度为水平向，宽度为竖向，加翼桩结构见图1。

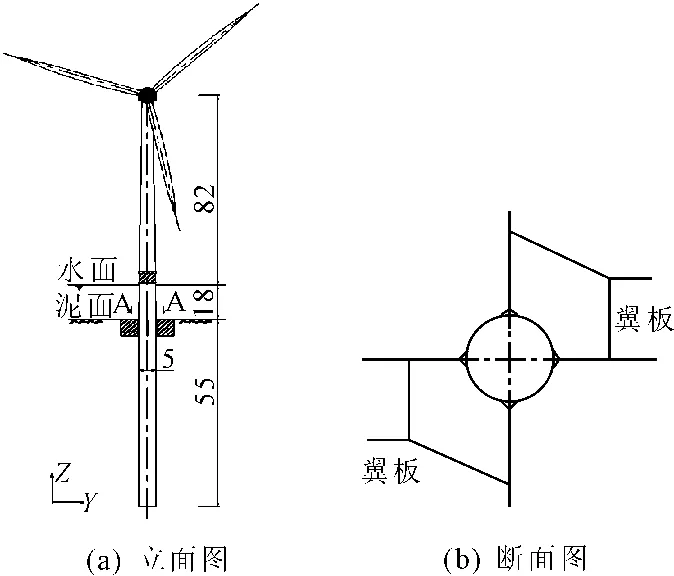
图1 加翼桩结构示意图

基于ABAQUS软件，建立三维实体有限元模型，水平向桩周土体取25倍桩径，土层总厚度取1．3倍入土深度。网格沿深度方向0．1 m～1．0 m间距划分，桩周环向按0．5 m间距加密网格。土体全局范围按每隔10．0 m划分一个单元，桩周土体作网格细化处理，桩体和土体单元采用C3D8R单元。钢板采用线弹性本构模型，地基土采用Mohr－Coulomb弹塑性本构模型。桩－土接触面采用主面－从面接触对算法计算，接触面单元设置为法向“硬接触”，摩擦系数μ按罚刚度法计算［5－7］。有限元模型以土体底面中心为坐标系原点，土体底面所在平面为 XY平面，基桩轴线为Z向，水平荷载沿 X轴通过翼板中心线加载。模型底部边界设置固定约束，四周边界设置水平位移约束。以某5MW级海上风电机组为模型，考虑水平向风、浪、流等荷载，按50年一遇荷载组合工况，计算时将水平荷载简化为集中力沿一组翼板中心线作用于距泥面18 m的桩顶横截面中心。

钢管桩及翼板为Q345钢，密度7 850 kg／m3，弹性模量206 GPa，泊松比0．3。地基为粉质黏土，密度 1 960 kg／m3，黏聚力 25．0 kPa，内摩擦角 14°，泊松比0．3，土体弹性模量按4倍压缩模量取值为30．0 MPa［8－9］。假定加翼桩最大应力达到材料允许强度或桩身泥面处倾斜率达到4‰时，为水平极限承载状态［10－11］。

对建立的模型进行可靠性验证，通过海洋高桩基础水平大变位模型试验结果［12－13］的对比，水平荷载作用下桩身屈服前后不同深度桩身弯矩和位移试验值与模型计算值吻合较好。

2 翼板刚度的影响分析

翼板刚度直接影响水平荷载作用下与土体相互作用后产生的弯曲变形，由于材料特性、厚度、结构形式等因素影响其刚度，计算时为了简化以面积5 m×5 m、壁厚0．08 m、上缘与泥面同高的钢翼板为基准，取相对刚度（EI／E0I0）为 0．6、0．8、1．0、2．0 和4．0的翼板进行计算分析，分别以 FPEI1、FPEI2、FPEI3、FPEI4和 FPEI5表示。

2．1 桩身位移

根据计算，得到翼板刚度与泥面处水平位移关系曲线见图2，12．0 MN荷载作用下翼板相对刚度4．0的加翼桩水平位移云图见图3。计算结果表明：泥面处水平位移随翼板刚度增大而减小，但影响程度总体较小，翼板相对刚度4．0比相对刚度为0．6的加翼桩在1．5 MN和12．0 MN荷载作用时泥面处水平位移分别只降低1．4%和2．3%。

桩身水平位移初始零点位置随翼板刚度增大而升高，1．5 MN～12．0 MN作用时桩身水平位移初始零点出现在泥面下4．04D～4．92D范围。

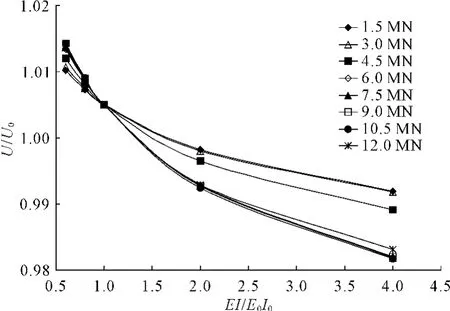
图2 翼板刚度与泥面处水平位移

2．2 桩身弯矩

根据计算，得到翼板刚度与桩身最大弯矩曲线见图4。

图3 加翼桩FPEI5水平位移云图（H＝12．0MN）

图4 翼板刚度与桩身最大弯矩

加翼桩桩身最大弯矩随翼板刚度增大而先减小后增大，但总体影响效果较小，12．0 MN荷载作用下翼板相对刚度4．0比相对刚度0．6的加翼桩桩身最大弯矩值仅降低1．6%。

加翼桩最大弯矩位置随水平荷载增大而降低，随翼板刚度增加而升高，水平荷载1．5 MN～13．5 MN作用时最大弯矩位置在泥面下0．68D～1．64D；极限荷载作用时，最大弯矩位置在泥面下1．49D～1．52D。

2．3 桩身应力与水平极限承载力

根据计算，得到不同翼板刚度加翼桩在12．0 MN水平荷载作用下的应力云图见图5，水平荷载作用下桩身最大应力和泥面处倾斜率见表1，不同刚度翼板加翼桩水平极限承载力与相应应力计算结果见表2。从表1、表2可得以下结论：

（1）翼板刚度对加翼桩桩身最大应力影响相对较大，翼板刚度越大桩身最大应力越大，12．0 MN荷载作用下翼板相对刚度4．0比相对刚度0．6的加翼桩桩身最大应力增大了14．9%。

（2）翼板刚度对桩身与翼板连接处的应力影响较桩身应力的影响更大。随着翼板刚度与桩身刚度比增大，翼板与桩身连接处应力增大迅速，12．0 MN荷载作用下翼板相对刚度4．0比相对板刚度0．6时增大了221．8%。

（3）桩基泥面处倾斜率随翼板刚度增大而减小，12．0 MN水平荷载作用下翼板相对刚度4．0比相对刚度0．6的加翼桩桩基泥面处倾斜率降低了2．6%。

（4）加翼桩水平极限承载力随着翼板刚度增大而先增大后减小，当翼板刚度与桩身刚度接近时，极限承载力受泥面处倾斜率或桩身最大应力控制，而当翼板刚度明显大于桩身刚度时，极限承载力受翼板与基桩连接处最大应力控制，根据计算结果，相对刚度1．0～2．0为合理的翼板与桩身刚度比。

图5 不同翼板刚度加翼桩桩身应力云图（H＝12．0 MN）

3 翼板埋深的影响分析

以面积5 m×5 m、壁厚0．08 m的钢翼板为模型，分别取翼板埋深 Z（上缘至泥面的距离）为0 m、1．0 m、2．5 m 和 4．0 m（分别以 FPZ0、FPZ1、FPZ2 和FPZ3表示）的加翼桩模型计算，提取桩身变形、弯矩、结构应力、泥面处桩身倾斜率和极限承载力等结果进行分析［14－15］。

3．1 桩身位移

根据计算，得到翼板埋深Z与泥面处水平位移曲线见图6，12．0 MN水平荷载作用下翼板埋深1．0 m时加翼桩水平位移云图见图7。

表1 不同翼板刚度桩身最大应力和泥面处倾斜率

表2 不同翼板刚度极限状态下水平承载力与最大应力

图6 翼板埋深与泥面处水平位移关系

图7 翼板埋深1．0 m水平位移云图（H＝12．0MN）

由图6、图7可看出，加翼桩泥面处水平位移随翼板埋深增大先减小后增大，翼板埋深为1．0 m（0．2D）时加翼桩泥面处水平位移最小。12．0 MN水平荷载作用下翼板埋深1．0 m（0．2D）时比埋深为0．0 m的加翼桩泥面处水平位移降低5．6%，比翼板埋深 2．5 m（0．5D）和 4．0 m（0．8D）的加翼桩泥面处水平位移降低9．7%和12．5%。

桩身水平位移初始零点位置随翼板埋深 Z增大先升高后降低，水平荷载1．5 MN～12．0 MN作用时水平位移的初始零点位置在泥面下3．98D～4．85D 范围。

3．2 桩身弯矩

根据计算，得到翼板埋深Z与桩身最大弯矩值关系曲线见图8。由图8可看出，加翼桩在水平荷载作用下最大弯矩值位置随着翼板埋深 Z的增大而先升高后降低，极限荷载作用时最大弯矩位置在泥面下（1．52～ 1．54）D。

桩身最大弯矩随翼板埋深 Z增大先减小而后增大，翼板埋深1．0 m时最小。12．0 MN水平荷载作用下翼板埋深为1．0 m时分别比翼板埋深为0．0 m、2．5 m和4．0 m的加翼桩桩身最大弯矩值降低1．5%、2．0%和3．5%。翼板埋深对桩身最大弯矩值的影响相对较小。

图8 翼板埋深与桩身最大弯矩值关系曲线

3．3 桩身应力与水平极限承载力

根据计算，得到翼板不同埋深加翼桩在12．0 MN荷载作用下桩身应力云图见图9，水平荷载作用下桩身最大应力和泥面处倾斜率计算结果见表3，不同翼板埋深加翼桩水平极限承载力及相应应力见表4。

由表3、表4及图9可知随着翼板埋深 Z的增大，桩身最大应力逐渐由桩前受压区转移至桩后受拉区，桩前受压区最大压应力出现在桩前下缘与基桩连接处，桩后受拉区最大拉应力出现在桩后上缘与基桩连接处。

表3 不同翼板埋深加翼桩桩身最大应力与泥面处倾斜率

表4 不同翼板埋深加翼桩水平极限承载力与相应应力

图9 不同翼板埋深加翼桩桩身应力云图（H＝12．0 MN）

翼板埋深对加翼桩桩身最大应力的影响规律不甚明显，但埋深为0．0 m时桩身最大应力最小，12．0 MN 作用下，埋深为 0．2D、0．5D、0．8D 比埋深为 0．0 D时的最大桩身应力分别增加 10．1%、8．7%和15．5%。

加翼桩桩身倾斜率随翼板埋深 Z的增大先减小后增大，翼板埋深0．2D时加翼桩桩身泥面处倾斜率最小。12．0 MN水平荷载作用下，翼板埋深0．2 D时比翼板埋深为0．0 D和0．8D的加翼桩桩基泥面处倾斜率分别降低了5．3%和9．6%。

加翼桩水平极限承载力随着翼板埋深 Z的增大先增大而后减小，翼板埋深0．2D时加翼桩水平极限承载力最大，为13．12 MN。

4 结 语

以海上风电场大直径加翼桩为模型，基于ABAQUS有限元构建了加翼桩的三维数值仿真模型，选择5种翼板刚度、4种翼板埋深，研究了其对加翼桩桩身位移、桩身弯矩、桩身应力及水平极限承载力的影响。

（1）随着翼板刚度的增加，加翼桩泥面处水平位移随之减小，而桩身弯矩先减小后增大，但影响程度不大。12．0 MN荷载作用时，翼板相对刚度4．0时比相对刚度0．6时加翼桩水平位移减小2．3%，桩身弯矩仅降低1．6%。

（2）翼板刚度对桩身最大应力、桩身与翼板连接处应力影响较大，12．0 MN荷载作用下翼板相对刚度4．0时比相对刚度0．6加翼桩桩身最大应力增大了 14．9%，桩身与翼板连接处的应力增大了221．8%。

（3）加翼桩水平极限承载力随着翼板刚度增大先增大而后减小，当翼板刚度与桩身刚度接近时，极限承载力受泥面处倾斜率或桩身最大应力控制，而当翼板刚度明显大于桩身刚度时，极限承载力受翼板与基桩连接处最大应力控制，相对刚度1．0～2．0为合理翼板与桩身刚度比。

（4）加翼桩泥面处水平位移随着翼板埋深增大先减小而后增大，而最大弯矩值位置随着翼板埋深Z的增大而先升高后降低。翼板埋深对水平位移的影响大于对弯矩的影响，翼板埋深1．0 m（0．2D）时比埋深4．0 m（0．8D）加翼桩泥面处水平位移降低12．5%，桩身最大弯矩降低 3．5%（12．0 MN）。

（5）翼板埋深为0．0 m时加翼桩桩身最大应力最小，埋深 Z对桩身最大应力的影响规律不明显。翼板埋深 1．0 m（0．2D）时比埋深 0．0 m、4．0 m（0．8D）桩身泥面处倾斜率分别降低了5．3%和9．6%。

（6）加翼桩水平极限承载力随着翼板埋深Z的增大先增大而后减小，翼板埋深0．2D时加翼桩水平极限承载力最大。

［1］ 黄维平，刘建军，赵战华．海上风电基础结构研究现状及发展趋势［J］．海洋工程，2009，27（2）：130-134．

［2］ 王 伟，杨 敏．海上风电机组地基基础设计理论与工程应用［M］．北京：中国建筑工业出版社，2014．

［3］ 王曦鹏，陈灿明，苏晓栋，等．水平静荷载作用下翼板对基桩工作性状影响的有限元研究［J］．水道港口，2016，37（6）：609-614．

［4］ 王曦鹏．加翼桩水平承载力影响因素及计算方法研究［D］．南京：河海大学，2017．

［5］ 于仁斌，范庆来，郑 静．海上风机加翼桩水平受荷简化分析模型研究［J］．地下空间与工程学报，2016，12（S1）：113-119．

［6］ 费 康，张建伟．ABAQUS在岩土工程中的应用［M］．北京：中国水利水电出版社，2010．

［7］ 王继成，潘晓东，丁翠红．翼板、承台埋深对桩水平承载力的影响研究［J］．人民长江，2007，38（8）：162-164．

［8］ 于丽鹏．基于FLAC3D模拟的土体弹性模量取值分析［J］．水利与建筑工程学报，2014，12（2）：162-166．

［9］ 张江涛，豆红强，王 浩．滨海软土地区综合管廊基坑开挖钢板桩支护性状分析［J］．水利与建筑工程学报，2016，14（6）：120-125．

［10］ 中海石油研究中心．海上固定平台规划、设计和推荐作法——工作应力设计法：SY／T 10030—2004［S］．北京：石油工业出版社，2004．

［11］ 水电水利规划设计总院．风电机组地基基础设计规定：FD 003—2007［S］．北京：中国水利水电出版社，2007．

［12］ 朱 斌，朱瑞燕，罗 军，等．海洋高桩基础水平大变位性状模型试验研究［J］．岩土工程学报，2010，32（4）：521-530．

［14］ 苏航州，段 伟，段晓伟，等．水平荷载作用下 GRF桩基础受力特性的数值分析［J］．水利与建筑工程学报，2015，13（3）：200-204．

［15］ 孙 希，黄维平．基于数值模拟的海上风电大直径桩桩土相互作用研究［J］．水力发电，2015，41（3）：72 －75．