改进的DataMatrix码L形边精确定位方法
2018-03-20郭浩铭田劲东
李 东,郭浩铭,田劲东,田 勇
深圳大学光电工程学院,广东深圳 518060
DataMatrix(DM)码因具有尺寸小、纠错能力强,以及较强的抗污染和抗畸变能力,被广泛用于工业和物流领域中.DM码依靠一个L形特征边和一对切换边组成定位图形,通过定位图形可在复杂背景中定位出DM码,并以此对DM码进行采样和识别,DM码的定位图像和数据区域如图1.

图1 DM码符号Fig.1 DM code symbol
目前,对于DM码的定位和条码方向确定主要通过定位DM码的L形特征边实现[1-2].Hough变换(Hough transform,HT)是一种经典的直线检测方法,常用于定位DM码的L形边[3-7].但在实际应用中由于非直线目标边缘像素的存在,容易污染Hough变换域,干扰实际直线的检测,甚至出现伪峰,产生“虚假直线”问题.另外,Hough变换法由于存在Hough变换域的量化误差,其精度受空间和时间开销所限制,单独依靠Hough变换法进行直线定位不适于实时性能要求高的嵌入式设备.
为提高传统Hough变换法的定位精度,乔寅骐等[8]提出利用最小二乘法拟合直线参数,并将其用于随机Hough变换投票方法,通过对采样点周围ρ-θ域进行最小二乘法拟合,以提高投票精度,由于随机Hough变换法是一种通过牺牲采样点换取较高定位速度的方法,并未解决Hough变换法的系统误差.郭斯羽等[9]提出结合Hough变换与改进最小二乘法的直线拟合方法,通过Hough变换法得到直线的大致区域,再通过迭代剔除距离拟合直线最远的点,以保证样本的准确性,以期得到较好的拟合直线,该方法解决了Hough变换法的系统误差,但由于精度和耗时与人为设定的样本点数量有关,不适用于实际应用中复杂的图像情况.WILLIAM[10]提出将迭代加权最小二乘法(iteratively reweight least squares,IRLS)用于直线拟合的方法,且MICHIEL等[11]论证了加权最小二乘法的鲁棒性.
本研究在分析传统Hough变换优缺点的基础上,从剔除干扰边缘,减少Hough变换运算量,提高定位边精度3方面入手,提出一种结合Hough变换法和迭代加权最小二乘法的DM码L边方法,定位流程如图2,其中,m1,m2, …,mn均为候选轮廓.实验结果表明,该方法能在嵌入式设备上快速、准确地定位DM码L边.
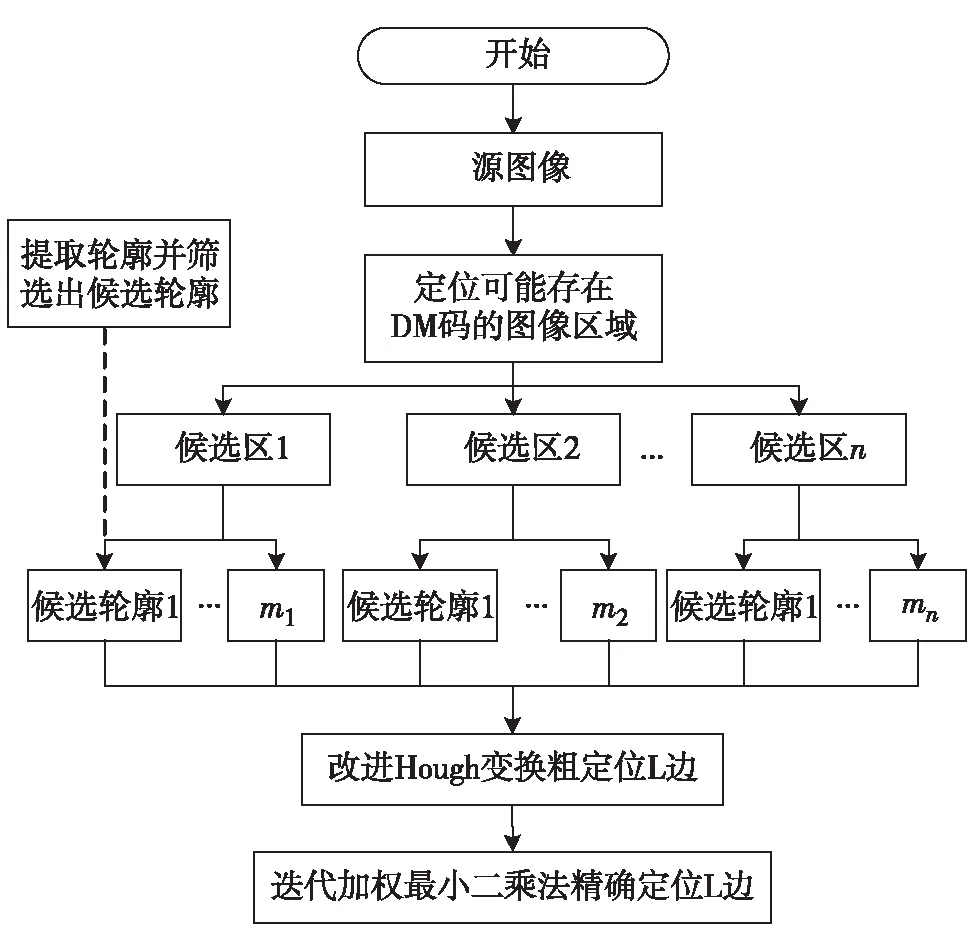
图2 DM码精确定位流程Fig.2 The flowchart of DM code precise positioning
1 DM码区域粗定位
基于纹理特点对二维条码进行定位的方法主要是通过定位角点密集区域实现,其优点是抗干扰能力强,能快速定位二维条码存在的区域,常通过基于SUSAN和Harris算子提取角点实现[12],而角点检测(features from accelerated segment test, FAST)方法因运算速度快而常用于对实时性能要求高的嵌入式系统[13].
为快速获取图像中的角点信息,本研究使用FAST-9检测方法对图像进行角点提取[14].在得到角点图后进行网格划分,对每个格子内的角点进行统计,以得到单位空间内的角点密度,最终获得角点密度图G,其中,每一块区域用gi表示.图3(a)的角点密度图G如图3(b).
因经过预处理后,背景多为平坦或直线区域,角点密度不大,故可取一个整体阈值区分角点密集与稀疏的部分.将分布图看作一幅灰度图像,背景为角点稀疏区域,即灰度值小的区域,前景为角点较密集的区域,即灰度值较大的区域.最大类间方差(OTSU)法是一种通过计算最大类间方差以获得分割图像前景与背景灰度阈值的方法,本研究采用该方法进行图像分割,突出角点密集区域,效果如图3(c).
实际应用中DM码周围可能存在其他角点丰富区域,若这些区域与DM码接近,则在角点分布图G中可能存在部分连接块gi. 为断开这些连接,本方法通过对图像进行填孔操作和开运算操作.最终效果如图3(d),其中,亮色区域为角点分布图G中的角点密集部分,即DM码的搜索候选区.可见,其正好囊括DM码的主体部分.

图3 粗定位DM码Fig.3 (Color online) Rough locating of DM code
为提高DM码搜索的速度,对上述得到的候选区按照可能存在DM码的概率进行排序.
首先,筛选出可能存在条码的区域,假设认为条码都是正方形的,所以,可对连通域的形状进行约束.设连通域的宽高比小于r, 且具有的格子数量大于设定的阈值.

(1)
连通域的排序方法如下:对连通域按p1值从大到小排序,若有两个连通域的p1值相等,则按p2值从大到小排序.排序后的图像区域如图3(e),以连通域所在的外界矩形区域(矩形框内部图像)作为后续处理的图像区域.
对排序好的连通域依次进行后续的DM码定位处理,可快速找到DM码,提高计算效率.特别是当视场中DM码的数量已知时,本方法可减少无效区域的搜索计算,缩短DM码定位时间.
2 提取轮廓
DM码L边由两条相交直线构成,对L边的定位一般都需要进行边缘提取,再做Hough变换查找直线.DM码的外轮廓点集区域是用于L边定位的有效数据.然而,由于DM码区域内部含有大量的小码块,直接做边缘提取会产生很多无效的码块边缘信息,这些边缘点不仅增加边缘提取和Hough变换的运算量,更易污染Hough变换域,影响特征边的定位,因此,需要进行预处理,消除DM码内部码块边缘,并获取外轮廓点集.
形态学开运算因其具有融合断开区域,且保留原来图像轮廓的特点,常用于消除图像细节.考虑到开运算的结构元素大小需根据所处理图像的特征尺寸确定后,才能取得好的效果.因此,对于不同成像大小的DM码无法设置一个固定的通用值.为解决这个问题,本研究提出一种自适应处理方法,对前面所提取的DM码候选区域进行归一化缩放,从而保证固定尺寸的结构元,能对存在DM码的候选区产生较好的融合效果.
以下以图3(e)的区域1为例,按上述思路进行轮廓提取.根据角点密度提取出候选区域后,根据候选区域的坐标在原图中提取出待处理图像,并缩放到256×256的图像尺寸;对图像进行二值化处理,得到条码特征明显的二值图像;使用1个尺寸为9×9的结构元进行开运算处理,以消除条码内部的细节.结果如图4,该图已经过一次反色处理,黑色区域为背景.

图4 消除DM码细节Fig.4 Elimination of DM code details
对细节融合后的图像求边缘及边缘的连通域C. 为提高定位的鲁棒性,可以对提取出的边缘连通域加入约束,本研究提出以图像中轮廓的宽高比和轮廓所占面积作为轮廓的约束条件.
对连通域集合C根据式(2)和式(3)进行筛选,得到集合S.
S= {s|f(s)
(2)
(3)
其中,s表示集合C的元素;sw与sh表示连通域s的宽和高;f(s)表示目标轮廓的宽高比;g(s)表示轮廓所占的面积.
如前所述,对连通域按存在DM码的可能性排序,将尽可能减少处理时间.由于当前图像是在原图中粗定位得到的,目标条码应在当前图片中占有较大的像素面积,故可将图像中轮廓所占的面积作为判断轮廓是否条码的可信程度.本方法按元素包括的面积g(s)对集合S排序.
3 特征边定位
传统Hough变换方法需遍历图像域中的每一个边缘点,运算效率低.在嵌入式设备中,三角函数运算开销较大,通常采用查表的方法代替计算三角函数,以提高响应速度,但由于寻址操作并不能进行软件流水加速,所以,在1个循环中重复查表同样会降低设备运行效率.另外,当ρ的计算值为负数时, 并不在Hough变换域内, 当前计算为无效值.
3.1 改进Hough变换粗定位L边
本方法根据三角函数关系和直线在极坐标下的特性,减少三角函数的查表次数和限制θ的定义域区间,在不减少统计点的基础上提高运算效率.
对于Hough变换域下的曲线h(θ,ρ), 与图像域中的点(x,y)具有以下换算关系
ρ=xcosθ+ysinθ

(4)
根据三角函数性质将式(5)转换成式(6),其中,θ∈[0, 90). 将图像域根据左上角为坐标原点,向右为x轴正方向,向下为y轴正方向,建立直角坐标系.式(5)中的I、II、III、IV表示坐标轴原点在直线上的投影点所在的象限.

(5)
其中,ρ1(θ)=xcosθ+ysinθ;ρ2(θ)=xsinθ-ycosθ.
由此容易分析得图像域中的直线只可能经过第Ⅰ、Ⅱ及Ⅳ象限,故极角的取值范围为[0°,180°]∪[270°,360°],即式(5)可进一步化简为
(6)
传统Hough变换方法的查表次数与乘法次数均为2×n×360; 而改进的Hough变换方法分别为2×n×90和4×n×90(取角度步长为1°).可见,当前方法的查表次数仅为传统方法的1/4,乘法次数为传统方法的1/2.
3.2 迭代加权最小二乘法精确定位L边
Hough变换方法是将图像域中的点映射成Hough变换域中的三角函数曲线,在图像域中位于同一直线上的点,在Hough变换域中的曲线会相交于同一点.由于Hough变换域的每一个单元是一个自定义精度的统计格子,此量化过程会给直线定位引入量化误差.另外,由于图像域中的线段不一定属于单一直线,可能由于印刷问题或畸变导致直线出现锯齿或弯曲,在Hough变换域中的投票值不集中于一个格子,导致从Hough变换域映射回图像域的直线与原直线存在偏移或偏转.
IRLS法是对最小二乘法的改进,该方法通过在每次迭代中根据点到拟合直线的距离对样本进行加权,从而使拟合直线逐渐收敛于真实直线,不受干扰点影响.为精确得到DM码的L边,本方法采用迭代加权最小二乘法对Hough变换法得到的直线区域内的点集进行拟合,具体算法步骤如下.
步骤1根据Hough变换域中得到的目标点计算图像域中的直线方程l1和l2,以及两直线的交点c.
步骤2从点c出发,分别向直线l1和l2各自的方向生长,统计一定区间内的像素值,以确定DM码L形边辐射的方向O1和O2.
步骤3从点c出发,分别以O1和O2为生长方向,对点集s进行查找,并将点保存在点集Ln中,n=1, 2.
步骤4设权为1,对点集L进行最小二乘法拟合,得到直线lfn0.
步骤5计算点集Ln中的点到直线lfni的距离,以各点距离的倒数为权,得到集合wni,i=0,1,….
步骤6使用集合wni对点集Ln加权,重新使用最小二乘法计算拟合直线,得到直线lfn(i+1).
步骤7计算两直线lfn(i+1)与lfni之间的误差,若小于设定误差值ε,则退出迭代,否则i=i+1, 重复步骤5.
4 实验与分析
为验证本研究所提出方法的性能,设计以下试验.在TI公司的TMS320DM648处理器上进行,处理器的主频为864 MHz,采集的图片分辨率为640×480像素.
图5(a)、(b)和(c)是传感器采集到的原始图像,列举了在低对比度、背景复杂及透视畸变的情况下,本方法的识别能力.图5(a)是电池充电器插座外壳上使用激光刻蚀造成的DM码,其被文字环绕,且条码与背景对比度低;图5(b)是一张说明书上印刷的DM码,图像中存在大量文字和线条;图5(c)是图5(b)的目标物体在倾斜角度下拍摄的图像,目标条码产生严重的透视畸变.
图5(d)、(e)和(f)分别是图5(a)、(b)和(c)的定位结果.这些测试案例说明,本方法在复杂背景、低对比度及透视畸变的情况下,依旧具有高准确度和高鲁棒性的特点.
传统几何定位方法通过对图像进行Hough变换定位L边,然后查找平行的切换边得到DM码的4个顶点位置,再通过采样得到数据矩阵,进行解码,从而识别出条码的内容.
为对比本方法与传统几何定位方法在性能上的区别,设计如下实验.实验在TI公司的TMS320DM648处理器上进行,处理器的主频为864 MHz,采集的图片分辨率为640×480像素,使用1个旋转平台,让相机在不同角度对目标条码进行识别.使用传统的几何定位方法和本研究提出的定位方法分别进行测试,连续读取10 000张图片后,得到几何方法的识别率和平均耗时分别为41.8%和253 ms,本研究方法的识别率和平均耗时分别为99.9%和64 ms.
传统的几何定位方法对于简单图案能快速定位,但对于背景复杂或干扰较多的情况,由于非边缘点参与计算,影响Hough变换对特征边的定位效果,导致条码识别率不高.本研究所提方法通过2次轮廓筛选和2次直线定位,在复杂环境中也可高速精确地定位DM码,较传统方法在识别率和耗时上有着明显提高.

图5 DM码定位结果Fig.5 (Color online) Results of DM code location
结 语
本研究提出一种DataMatrix二位条码L形特征边定位方法,实现对复杂背景情况下DM码的快速、准确定位.本方法通过4个主要步骤对L形特征边进行定位:① 根据角点分布粗定位候选区并排序,对候选区,减少算法的运算量,提高运算速度;② 对候选区做自适应的形态学处理,减少DM码内部细节,提高边缘定位精度和速度;③ 提出改进的Hough变换方法进行DM码L边粗定位,大幅提高计算效率;④ 提出采用迭代加权最小二乘法对Hough变换法定位的L边区域进行精确拟合.实验结果表明,本算法对低对比度、背景复杂及透视畸变等DM码图像定位具有高准确性和强鲁棒性,计算效率提高约4倍.
/
[1] 李 梅.物联网科技导论[M].北京:北京邮电大学出版社,2015:17-19.
LI Mei. Introduction to science and technology[M]. Beijing: Beijing University of Posts and Telecommunications Press, 2015:17-19.(in Chinese)
[2] 胡晓岽,何加铭.Data Matrix码识别技术研究[J].杭州电子科技大学学报,2008,28(5):124-126.
HU Xiaodong, HE Jiaming. The technology research of decoding DataMatrix code[J]. Journal of Hangzhou Dianzi University, 2008, 28(5): 124-126.(in Chinese)
[3] 王根源,吴祥坤,胡 坤,等.DataMatric码的嵌入式识别算法[J] .吉林大学学报信息科学版,2016,34(3):419-426.
WANG Genyuan, WU Xiangkun, HU Kun, et al. Embedded recognition of DataMatrix code by using cross correlation matching algorithm and Hough transform[J]. Journal of Jilin University Information Science Edition, 2016,34(3): 419-426.(in Chinese)
[4] MOSS C, CHAKRABARTI S, SCOTT D W. Parts quality management: direct part marking of data matrix symbol for mission assurance[C]// Aerospace Conference. Big Sky, USA: IEEE, 2013:51-52.
[5] 陈文艺,陈蓓敏.基于复杂背景的二维条码提取技术[J].西安邮电大学学报,2014,19(2):48-51.
CHEN Wenyi, CHEN Beimin. Extraction technology of 2-D barcode under complicated background[J]. Journal of Xi’an University of Posts and Telecommunications, 2014, 19(2): 48-51.(in Chinese)
[6] 袁远松,赵小敏,杨东勇.DataMatrix条码的畸变校正[J].计算机系统应用,2008(10):47-50.
YUAN Yuansong, ZHAO Xiaomin, YANG Dongyong. The correction of DataMatrix barcode distortion[J]. Journal of Xi’an University of Posts and Telecommunications, 2008(10): 47-50.(in Chinese)
[7] 王 伟,何卫平,雷 蕾,等.污染及多视角下DataMatrix码精确定位[J].计算机辅助设计与图形学学报,2013,25(9):1345-1353.
WANG Wei, HE Weiping, LEI Lei, et al. Accurate location of polluted DataMatrix code from multiple views[J]. Journal of Computer-Aided Design & Computer Graphics, 2013, 25(9): 1345-1353.(in Chinese)
[8] 乔寅骐,肖健华,黄银和,等.基于最小二乘法修正的随机Hough变换直线检测[J].计算机应用,2015,35(11):3312-3315,3320.
QIAO Yinqi, XIAO Jianhua, HUANG Yinhe, et al. Randomized Hough transform straight line detection based on least square correction[J]. Journal of Computer Applications, 2015,35(11): 3312-3315, 3320.(in Chinese)
[9] 郭斯羽,翟文娟,唐 求,等.结合Hough变换与改进最小二乘法的直线检测[J].计算机科学,2012,39(4):196-200.
GUO Siyu, ZHAI Wenjuan, TANG Qiu, et al. Combining the Hough transform and an improved least squares method for line detection[J]. Computer Science, 2012, 39(4):196-200.(in Chinese)
[10] WILLIAM A P. Statistical teaching aids[D]. Worcester(USA): Worcester Polytechnic Institute, 2006.
[11] MICHIEL D, ANDREAS C, MIA H, et al. Robustness of reweighted Least Squares Kernel Based Regression[J]. Journal of Multivariate Analysis, 2010, 101(2): 447-463
[12] 周 乐.基于SUSAN检测算子的二维条码定位方法[J].微型机与应用,2012,31(9):35-37.
ZHOU Le. Location method of two-dimensional bar code based on the SUSAN detection operator[J]. Microcomputer & Its Applications, 2012, 31(9): 35-37.(in Chinese)
[13] 齐凤山,蒋廷耀.基于Harris的二维码图像角点检测方法改进[J].软件导刊,2016,15(5):199-201.
QI Fengshan, JIANG Tingyao. Improvement on 2-D code image corner detection based on Hasrris[J]. Software Guide, 2016,15(5): 199-201.(in Chinese)
[14] 郭莉沙,李俊山,朱英宏,等.基于多尺度FAST-9的图像快速匹配算法[J].计算机工程,2012,38(12):208-217.
GUO Lisha, LI Junshan, ZHU Yinghong, et al. Fast image matching algorithm based on multi-scale FAST-9[J]. Computer Engineering, 2012, 38(12): 208-217.(in Chinese)
