基于时延优化的软件定义网络控制层部署策略

樊自甫，姚 杰，杨先辉

(重庆邮电大学 下一代网络应用技术研究所，重庆 400065)(*通信作者电子邮箱542438256@qq.com)

0 引言

随着网络信息技术的飞速发展，传统网络架构无法满足日益增长的网络带宽以及数据分析等业务需求，亟须一种新型的支持动态扩展的创新网络架构，软件定义网络(Software Defined Network, SDN)随之应运而生。SDN是由美国斯坦福大学Cleanslate研究组提出的一种基于集中控制的新型网络架构,通过把网络的控制面和转发面分离，用集中控制器取代了原来的路由协议自协商方式，极大地提升了网络的管控效率，开放了网络能力。

在SDN架构中，控制器负责整个网络的集中化控制，对于把握全网资源视图、改善网络数据交付都具有非常重要的作用。随着SDN在大规模网络中的部署[1]，单一集中式的控制器已无法满足来自全网所有交换机的流处理请求，SDN在大规模网络中的部署面临着来自控制平面扩展性方面的严峻挑战[2]。在SDN中引入多台控制器是解决SDN性能瓶颈、难以横向扩展以及可靠性问题的主流趋势。然而，这种由多台控制器构成的分布式SDN控制层也带来了一些新的思考。其中一个核心问题是如何确定控制器的数量、部署位置以及如何划分每个控制器的管理区域，即SDN控制层的部署问题。

1 相关工作

针对SDN控制层的部署问题，当前学术界主要从最小化传播时延、提升网络可靠性以及均衡各控制器负载等几个方面展开。由于网络设备间的时延将会影响到转发规则的安装次序以及不同控制器间的状态同步，进而引发控制逻辑的不一致，大量研究者在考虑控制层部署问题时将时延作为首要优化目标。

文献[3]首次提出了SDN控制层的部署问题，并指出在传播时延占主导地位的广域网中，控制层的部署策略将严重影响到网络的收敛时间。作者在文章中引入了平均传播时延及最坏情况下的传播时延两种时延指标，采用真实的Internet 2拓扑分析了不同的控制器数量以及部署位置对交换机与控制器间传播时延产生的影响。文献[4]在最小化平均传播时延模型的基础上，将交换机的处理时延纳入考虑范围，并依据模糊集理论建立了一种新的时延优化模型。文献[5]采用谱聚类算法将广域网拓扑分区处理，继而在各个分区中找到合理的控制器部署位置，该算法在一定程度上降低了广域网中的传播时延。文献[6]同时考虑了流表建立时间以及控制器间的同步时延，对最小化时延模型作了进一步的优化。文献[7]采用K-Critical算法，通过构建robust树解决控制层的部署问题，该算法在保证网络时延的同时一定程度上提升了控制层的鲁棒性。

以上文献对SDN控制层的部署研究作出了一定的贡献，但仅仅只考虑了正常网络状态下时延对控制层的影响。本文以时延作为主要优化目标，并将网络中的链路故障因素纳入考虑范围。首先，以最坏情况时延作为控制层部署策略的衡量指标，综合考虑网络正常运行以及单链路故障等多种网络状态下的最坏情况时延，提出了一种新的时延指标，即网络状态时延并以此作为优化目标建立相应的数学模型。其次，提出了两种解决上述模型的启发式算法——基于贪婪算法的控制层部署算法(Controller Placement Algorithm based on Greedy Algorithm， GA-CPA)和基于粒子群算法的控制层部署算法(Controller Placement Algorithm based on Particle Swarm Optimization， PSO-CPA)。最后，利用真实网络拓扑数据进行仿真，对两种部署算法得到的最佳部署方案以及网络状态时延进行对比、分析。

2 数学模型建立

2.1 前提假设

依据SDN控制层关键技术的当前研究成果及控制层部署问题的主流研究思路作出以下几点合理假设。

假设1 由于带外模式通常会带来可靠性的下降，而且在工程上也难以实现。在大规模SDN中，控制网络的建立通常采用带内连接模式[8]，因此，本文研究场景设定为采用带内连接的广域SDN。

假设2 为进一步降低时延，同时增强控制网络的可靠性与安全性，控制器采用co-locate方式部署，即控制器的部署位置从网络中所有交换机位置及其邻近位置中选取，逻辑上可将控制器与其直接相连的交换机视为同一位置，因此，可以忽略两者间的传播延时。

假设3 由于控制网络的首要目的是快速、有效地传递控制信息，本文假定控制信息的主备路径均通过最短路径生成。此外，考虑到跨域通信的影响，当链路出现失效，若本域内存在另外一条可达路径，默认此路径为链路失效恢复所采用的备份路径。

假设4 通过对现有网络故障相关资料的梳理，发现大多数网络故障由极少量网络元件的失效引发，文献[9]通过对多个骨干网的实际测量指出，约70%的网络故障是由于单条链路的失效引起，多条链路同时失效的概率极低，因此，本文主要考虑单链路失效引发的网络故障。

2.2 控制层部署问题模型

对于给定的广域SDN可以通过无向图G(V,E)表示，其中V={v1,…,vi,…,vn}代表网络中所有交换机节点的集合，E={e1,…,ei,…,em}表示交换机节点间的双向链路集合。控制器集合通过C={c1,…,ci,…,ck}表示，其中C⊂V，即控制器的部署位置从交换机节点位置中选取。假设网络中需要部署的控制器数量为k，通过区域划分可以将网络G(V,E)分为k个互无交集的SDN控制域，每个控制域由一台控制器管理，即G={D1,…,Dj,…,Dk}。对于控制域Di内的控制器ci，其管理的交换机集合为Θci={vi1,…,vij,…,vil}。用d(vij,ci)表示网络正常状态下交换机vij与其所属的控制器ci通过最短路径通信产生的传播时延。d′(vij,ci)表示链路故障状态下交换机vij与控制器ci通过最短路径通信产生的传播时延。假定每条链路的状态仅考虑正常与故障情况，定义S={s0,s1,…,sj,…,sm}为网络状态集合，其中包含一个所有链路均正常工作的网络正常状态s0,以及m个相互统计独立的单链路故障状态{s1,s2,…,sm}。假设每条链路均有一定的概率出现故障，对于链路集合E中的链路ei，其故障概率可用pei表示。

由于网络中的链路故障将会导致部分交换机与控制器间的传播时延剧烈恶化，甚至难以满足正常通信的需求，因此，本文将网络中所有交换机与其所属控制器间通过最短路径通信所获得的传播时延的最大值，即最坏情况时延[3]作为主要衡量指标，其表达式如下：

(1)

由于每条链路仅有两种状态，因此，对于链路集合中的第i条链路ei，其正常工作的概率为(1-pei)，那么，网络正常工作的概率可表示为：

(2)

在该状态下经过概率加权后的最坏情况时延Lwc(s0)可表示为：

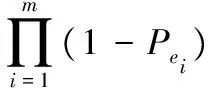
(3)

在考虑链路故障状态时，对各条链路的故障概率作标准化处理，链路ei的归一化故障概率可通过式(4)获得：

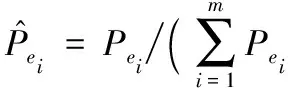
(4)

那么，由于链路ei失效而导致的网络故障，其概率可表示为：

(5)

在采用SDN架构的网络中，交换机与控制器间的通信路径通过链路层发现协议(Link Layer Discovery Protocol， LLDP)建立。一旦链路故障发生，故障链路两端的交换机尝试通过其相邻交换机向控制层作出故障报告，由控制层重新为其计算控制信息的通信路径或通过自愈收敛。这意味着，只要交换机与控制器间仍有任意一条路径存在，交换机就不会失去控制，因此，当链路发生故障，此时经过概率加权后的最坏情况时延可通过式(6)获得：

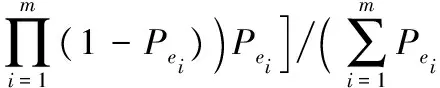
(6)

此外，在一种极端场景下，由于网络中某条链路发生故障导致该链路相关交换机与控制器失联成为孤立节点，即该交换机无法与控制器再次取得联系。针对这种情况可采用1+1备份的方式保证网络的可靠性[10]，因此不在本文考虑范围。

通过上述分析，提出一个新的时延指标，即网络状态时延(Network States Latency， NSL)，其公式如下：

(7)

由此，可得出本文模型：

minLNSL(S)

(8)

(9)

(10)

yvici,xvicj∈{0,1}

(11)

Di∩Dj=∅

(12)

Θc1∪Θc2∪…∪Θck=V

(13)

其中式(8)为本文的优化目标，即最小化网络状态时延(NSL)。该模型可视为一种多目标优化，即通过合理的部署策略保证较多网络状态下的最坏情况时延最小；式(9)将网络中的控制器数量限制为k个；式(10)确保网络中每个交换机有且只有一个控制器对其进行管理；式(11)为二元约束变量，若控制器ci部署于交换机vi的位置上，yvici为1，反之则为0；若交换机vi所属的控制器为cj，二元变量xvicj为1，反之则为0式(12)确保划分后的控制区域互不相交；式(13)则保证了控制区域的划分应覆盖网络中的所有交换机。

3 模型求解算法设计

最小化最坏情况时延的控制层部署问题[3]，可视为一类设施选址问题。这一类问题已被证明为NP-hard问题，难以在多项式时间内求解[11]。由于本模型是基于最小化最坏情况时延模型的一种改进，因此提出两种启发式算法，分别为基于贪婪算法的控制层部署算法(GA-CPA)以及基于粒子群算法的控制层部署算法(PSO-CPA)对模型进行求解。

3.1 基于贪婪算法的控制层部署算法

基于贪婪算法的控制层部署算法(GA-CPA)通过迭代的方式依次完成k个控制器的部署以及每个控制区域的划分。其中每一次外层循环的输入均基于上一次循环的最终输出结果。其具体步骤如下所示。

算法1 基于贪婪算法的控制层部署算法(GA-CPA)。

1)输入网络拓扑G(V,E)、控制器数量k、候选控制器位置集合C*←V、链路故障概率Pei← 0、当前控制器集合C← ∅、控制器ci所控制的交换机集合Θci← ∅；

2)计算网络正常状态下任意两交换机节点间的最短路径d(vi,vj)，生成最短路径矩阵matrixD[vi][vj]；

3)在C*中随机选取控制器的部署位置，根据最近邻原则完成控制区域划分，依据式(3)计算网络正常状态下经概率加权后的最坏情况时延Lwc(s0)；

4)为链路ei赋予故障概率pei，重新生成最短路径矩阵，根据式(6)计算此链路故障状态下经概率加权后的最坏情况时延Lwc(si)；

5)遍历链路集合E，依据式(7)计算该部署方案下的网络状态时延LNSL(S)；

6)遍历控制器候选位置集合C*，重复步骤2)至步骤5)，选择网络状态时延最小的位置作为首个控制器c1部署的位置；

7)更新控制器候选位置集合C*← {C*-c1}，更新当前控制器位置集合C← {C+c1}，在C*中选择第二个控制器的部署位置，直至k个控制器均完成部署，输出k个控制区域以及每个区域中控制器所在的位置，算法结束。

3.2 基于粒子群算法的控制层部署算法

依据实际问题，将粒子群中的粒子映射为控制器的部署方案。假设网络中部署k个控制器，那么粒子pi拥有一个k维的位置属性Xi=(xi1,xi2,…,xij,…,xik)与一个k维的速度属性Vi=(vi1,vi2,…,vij,…,vik)，其中控制器cj表示为粒子pi的第j维分量，其位置属性与速度属性分别为xij、vij。对于粒子pi，其局部最优解可表示为Pbesti=(pbesti1,pbesti2,…,pbestij,…,pbestik)。全局最优解则通过对比每个局部最优解获得，可表示为Gbest=(g1,g2,…,gj,…,gk)。粒子的适应度函数通过式(7)获得。

算法通过对粒子中每一维度的位置、速度更新，实现粒子的运动。式(14)、(15)分别表示粒子pi中第j维分量的位置与速度在第n+1次更新时的方式：

(14)

(15)

(16)

算法2 基于粒子群算法的控制层部署算法(PSO-CPA)。

Synthesis, properties and industrial applications of amino acid surfactants(To be continuted) 11 10

1)输入网络拓扑G(V,E)、控制器数量k、算法循环次数上限tmax、最大惯性权重wmax、最小惯性权重wmin。

2)初始化粒子与种群。随机选取k个位置部署控制器，依据最近邻原则将其余交换机节点分配给距其最近的控制器从而形成一种部署方案，随机选取N种部署方案形成粒子数目为N的种群。

3)初始化粒子速度。对于粒子pi，以其位置属性中的任一维度xij为核心，向其直接相连的交换机节点随机选择一次。记录xij到所选择节点的方向与距离作为粒子在该维度上的初始化速度方向与速度大小。粒子的速度由所有维度的速度构成，表示为Vi=(vi1,…,vij,…,vik)。

4)初始化局部最优解。将每个粒子的初始位置设置为局部最优解Pbesti←Xi。

5)初始化全局最优解。在局部最优解中选取适应度最好的粒子位置作为全局最优解Gbest←Xbest。

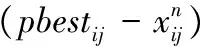
7)依据式(15)完成粒子位置更新。

8)局部最优解更新。根据式(7)计算当前位置的适应度，并与更新前粒子所在位置的适应度进行对比。若获得更好的适应度，则更新局部最优解；反之，则不变。

9)全局最优解更新。

10)检查全局最优解与当前迭代次数。若全局最优解达到收敛或当前迭代次数已达上限，算法结束；反之，返回步骤6)，进入下一次算法循环。

4 实验仿真

4.1 仿真环境及参数设置

为验证本文所提控制层部署策略的有效性，采用Matlab对相关参数进行实验仿真。实验采用的拓扑选自真实的Internet2[13]网络拓扑，该网络由美国多所高校及知名研究机构共同构建，旨在推进下一代网络建设。图1给出了Internet2网络拓扑的抽象视图。

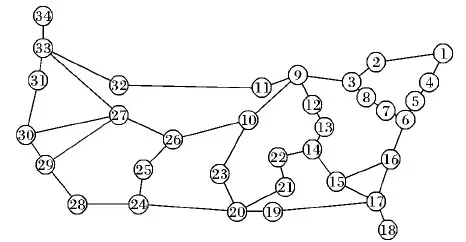
图1 Internet2拓扑

Internet2拓扑包括34个城市级网络节点以及41条链路。实验将交换机节点从1至34进行编号，每条链路的传输时延以节点间的距离乘2/3倍光速计算。实验中控制器采用co-locate方式进行部署，即控制器的部署位置在所有交换机位置中选取。考虑到网络链路的故障概率具有差异性，实验对于各链路的故障概率参数设置为区间[0,0.15]内的随机浮点数，其均值为0.04。

4.2 仿真结果分析

图2给出了两种算法与随机部署算法(RANdom Controller Placement Algorithm， RAN-CPA)在不同控制器数量下对于网络状态时延的对比结果。由图2可知，随着控制器数量的增加，两种算法所获得的网络状态时延均呈下降趋势，且PSO-CPA整体优于GA-CPA，而RAN-CPA性能最差。当控制器数目为1时，由于GA-CPA的每次部署循环均采用了遍历的手段，因此可获得实际上的全局最优解，从而优于PSO-CPA。

图2 不同控制器数量下的网络状态时延

图3 不同控制器数量下的时延收益

最小化网络状态时延模型的目标是通过合理的控制层部署策略保证较多网络状态下的最坏情况时延最小。图4给出了部署3个控制器时两种算法所得最坏情况时延的累积分布，其中PSO-CPA与GA-CPA将控制器分别部署于图1中编号27，14，7以及27，15，10的节点之上。由图4可知，在不同的网络状态下最坏情况时延将在8.19 ms至30.03 ms范围内大幅度波动，PSO-CPA与GA-CPA可以分别保证约44%及35%的网络状态下最坏情况时延不高于8.19 ms，即对于两种算法而言，分别约18与15种链路故障状态不会对最坏情况时延产生影响；而在15 ms范围内，该比值可分别达到95%与88%。由此可见，在链路发生故障时不同的控制层部署方案在保障最坏情况时延方面存在着优劣，而合理的部署策略可以使更多的链路故障状态下最坏情况时延所受影响较小。

图4 最坏情况时延累积分布

5 结语

在充分考虑了不同网络状态下传播时延的前提下，本文提出了基于时延优化的控制层部署方案。以最坏情况时延作为控制层部署策略的衡量指标，综合考虑了网络正常状态以及多种单链路故障状态，提出了一种新的时延指标，即网络状态时延并以此作为优化目标建立相应模型。同时，提出了两种启发式控制层部署算法，即PSO-CPA与GA-CPA对模型进行求解。仿真结果表明本文所提两种部署算法均能在不同程度上降低网络状态时延，从而保证了大部分网络状态下的最坏情况时延维持在较低范围。由于本文仅考虑了单链路故障状态下的时延，因此下一步工作计划及未来研究将会考虑多链路失效状态对时延的影响。

References)

[1] MCCAULEY J, PANDA A, CASADO M, et al. Extending SDN to large-scale networks [J]. Open Networking Summit, 2013, 58(2): 50-51.

[2] YEGANEH SH, TOOTOONCHIAN A, GANJALI Y. On scalability of software-defined networking [J]. IEEE Communications Magazine, 2013, 51(2): 136-141.

[3] HELLER B, SHERWOOD R, MCKEOWN N. The controller placement problem [J]. ACM SIGCOMM Computer Communication Review, 2012, 42(4): 473-478.

[4] 姚琳元,陈颖,宋飞.基于时延的软件定义网络快速响应控制器部署[J].电子与信息学报,2014,36(12):2802-2808.(YAO L Y, CHEN Y, SONG F. Delay-aware controller placement for fast response in software-defined network [J]. Journal of Electronics and Information Technology, 2014, 36(12): 2802-2808.)

[5] XIAO P, QU W, QI H, et al. The SDN controller placement problem for WAN [C]// ICCC 2014: Proceedings of the 2014 IEEE/CIC International Conference on Communications in China. Piscataway, NJ: IEEE, 2014: 220-224.

[6] 张联镇,黄传河,曾毓珑.SDN中基于时延优化的多控制器部署方案[J].计算机工程与设计,2015,36(5):1121-1125.(ZHANG L Z, HUANG C H, ZENG Y L. Multi-controller deployment scheme based on delay optimization in SDN [J]. Computer Engineering and Design, 2015, 36(5): 1121-1125.)

[7] JIMÉNEZ Y, CERVELL-PASTOR C, GARCA A J. On the controller placement for designing a distributed SDN control layer [C]// Proceedings of the 2014 International Federation for Information Processing Networking Conference. Piscataway, NJ: IEEE, 2014: 1-9.

[8] PANDA A, SCOTT C, GHODSI A, et al. CAP for networks [C]//

Proceedings of the 2013 ACM SIGCOMM Workshop on Hot Topics in Software Defined Networking. New York: ACM, 2013: 91-96.

[9] MARKOPOULOU A, IANNACCONE G, BHATTACHARYYA S, et al. Characterization of failures in an operational IP backbone network [J]. IEEE/ACM Transactions on Networking, 2008, 16(4): 749-762.

[10] ZHANG Y, BEHESHTI N, TATIPAMULA M. On resilience of split-architecture networks [C]// GLOBECOM 2011: Proceedings of the 2011 IEEE Global Telecommunications Conference. Piscataway, NJ: IEEE, 2011: 1-6.

[11] 潘锐，朱大铭，马绍汉.k-Median近似计算复杂度与局部搜索近似算法分析[J].软件学报,2005,16(3):392-399.(PAN R, ZHU D M, MA S H. Approximated computational hardness problem and local search approximated algorithm analysis fork-median problem [J]. Journal of Software, 2005, 16(3): 392-399.)

[12] MA L, FOROURAGHI B. A modified particle swarm optimizer for engineering design [C]// IEA/AIE 2012: Proceedings of the 2012 International Conference on Industrial, Engineering and Other Applications of Applied Intelligent Systems. Berlin: Springer, 2012: 187-196.

[13] Internet2. Internet2 open science, scholarship and services ex-change [EB/OL]. [2017- 03- 28]. http://www.internet2.edu/network/ose/.

This work is partially supported by the National Natural Science Foundation of China (61701064), the Scientific and Technological Research Program of Chongqing Municipal Education Commission (KJ1600424), the Doctor Research Startup Foundation of Chongqing University of Posts and Telecommunications (A2015- 41), the Science Research Project of Chongqing University of Posts and Telecommunications for Young Scholars (A2015- 62).

FANZifu, born in 1977, M. S., associate professor. His research interests include next generation network technology, communication operation management.

YAOJie, born in 1994, M. S. candidate. His research interests include next generation network technology, software defined network.

YANGXianhui, born in 1990, M. S. candidate. His research interests include next generation network technology, software defined network.