基于预测模型的轨迹数据压缩方法

陈 煜，蒋 伟，周继恩

(中国银联股份有限公司 银联科技事业部，上海 201201)(*通信作者电子邮箱jiangwei1@unionpay.com)

0 引言

随着定位技术的发展，人们可以很容易地通过全球定位系统(Global Positioning System， GPS)设备获得移动对象的实时位置信息，从而得到移动物体的运行轨迹。由于移动对象的运行状况具有连续性，需要不断地获取GPS采样点以便更好地通过离散的采样点拟合移动对象的运行轨迹。然而较高的采样频率会产生大量的GPS记录，给轨迹数据的存储、管理和分析带来巨大的挑战[1]。为了解决这个问题，大量的轨迹压缩算法通过对数据的时空特性进行分析，通过保存那些包含重要信息的采样点[2]，如转向点、速度剧烈变化点、车辆停止点等，来达到压缩轨迹的目的。

近几年来，随着城市路网结构数据的不断完善，结合路网结构的轨迹压缩变得可行。为了降低轨迹数据的误差，首先对原始轨迹进行路网匹配(Map-Matching)预处理[3-4]。由于路网结构信息往往是静态的并且结构相对固定，因此利用路网结构信息对轨迹进行约束，不仅可以有效地降低轨迹数据的数据规模,同时可以通过路网信息降低因GPS设备精度造成的数据误差[5]。

Cao等[6]提出的Nonmaterialized算法首次提出了利用路网结构对轨迹数据进行压缩。该算法首先将轨迹采样点数据通过路网匹配算法映射在路网上，然后通过Nonmaterialized算法将映射过的轨迹数据转化为路口序列，以达到压缩轨迹的目的。Lerin等[7]对Nonmaterialized算法进行改进，通过最短路径(Shortest Path)算法和链接算法来对轨迹数据进行进一步压缩。主要思想是:若轨迹行驶路径与最短路径一致时，只保留头尾两个路段;若行驶轨迹每次都沿着最小转角的路段行驶，那么也只用头尾两条路段来代替整段轨迹。两条路段间的最短路径可以通过Dijkstra算法[8]或者A*算法[9]计算得到，利用计算来对数据进行压缩。然而上述这些方法都没有考虑时间信息，无法知道压缩后的轨迹在某个时间点处于哪一个位置。

Kellaris等[10-11]提出的路网匹配轨迹压缩(Map-Matched Trajectory Compression， MMTC)算法把轨迹压缩问题转化成了函数最优化问题，主要思想是找到一条最适合的轨迹，使得这条轨迹尽可能地用最短路径表示，并且近似轨迹与原始轨迹相似度较高。MMTC算法用最小描述长度(Minimal Description Length， MDL) 模型来最优化压缩率和相似度组成的目标函数。在MMTC算法中，MDL模型由两个部分组成，分别是L(H)和L(D/H)，L(H)表示压缩后的轨迹长度，L(D/H)表示压缩后的近似轨迹与原始轨迹的误差。根据MDL原则，需要找到一条路径使得L(H)+L(D/H)最小，那么这条路径就满足目标条件。MMTC算法可以在压缩率和准确率两个方面得到很好的权衡，然而它同样没有考虑时间约束。

Song等[12]提出基于路网的并行轨迹压缩(Paralleled Road-network-based trajectory comprESSion， PRESS)算法，在MMTC算法的基础上对轨迹的时间信息和空间信息分别进行压缩。在空间信息方面，PRESS首先将GPS轨迹点映射在路网上，通过最短路径算法省略中间的路段，随后通过对一部分数据集进行训练，找到频繁的子轨迹。利用子轨迹的频繁度对轨迹进行霍夫曼编码，以此达到二次压缩的目的。这使得轨迹数据在空间方面是无损的，即压缩后的轨迹和原始轨迹是经过同一条路径的。在时间信息方面，PRESS通过提出时间同步路网距离(Time Synchronized Network Distance， TSND)和路网同步时间距离(Network Synchronized Time Difference， NSTD)两个误差度量，将时间压缩的误差控制在设定的误差范围，由此对轨迹数据的时间信息进行有损压缩。

然而上述方法，如MMTC算法[10-11]和PRESS算法[12]都是基于一种假设，即假设轨迹总是沿着路网中最短路径行驶的，因此这两种算法通过将轨迹的运动轨迹以最短路径的形式表示，从而达到轨迹压缩的目的。然而，在现实生活中，由于受到交通状况的限制，如交通信号灯、道路拥堵状况、道路施工和交通事故等，大部分移动物体并不能按照行程最短的路径行驶。

为了解决上述问题，本文基于路网信息结构提出了基于预测模型的轨迹数据压缩方法(Compression method for Trajectory data based on Prediction Model, CTPM)。由于移动对象的运动受到交通状况的限制，使得轨迹数据往往具有重复性和周期性。比如，由于受到上班高峰期的影响，从住所到上班地点通常会行驶在用户偏好的路径上，这条路径往往是通过对历史交通状况的判断而选择的一条最优路径，同时这条路径往往会在工作日内每天重复，因此，通过对历史轨迹数据进行学习，得到轨迹运行的预测模型，通过预测模型对轨迹数据进行压缩，将预测成功的采样点删除，保留那些预测失败的采样点作为轨迹关键点存储。

1 相关背景及问题定义

CTPM整体上分为学习和压缩两个阶段。在学习阶段，大量历史的GPS轨迹数据作为输入，经过噪点过滤等预处理步骤后进行路网匹配，通过路网匹配算法[3-4]，可以将欧氏空间的轨迹数据映射在路网结构上从而得到路网轨迹。然后对路网轨迹的空间信息和时间信息分别进行学习，生成预测模型。利用该预测模型，将轨迹数据时间信息和空间信息分别进行压缩，使得压缩后的轨迹数据在空间维度上无损，且时间维度上误差有界。与PRESS相似，将空间和时间这两种特征维度完全不同的信息分别考虑，从而取得更好的压缩效果。下面给出本文相关概念的形式化定义。

定义1 路网。路网结构被定义为一个有向图G(V,E)，其中：V是节点集合，E是边集合。每条边e上的权重，记作w(e)，可以表示该路段的路径长度、通行时间或速度限制。

定义2 轨迹。一条轨迹表示一个移动对象在对应时间维度下通过的路径，同时包含时间和空间两方面信息。在传统的轨迹表示方法中，一条轨迹被表示为GPS采样点pi=(xi,yi,ti)的序列的形式，即τ=〈p1,p2,…,pm〉，其中(xi,yi)表示物体在时间ti时的欧氏空间位置坐标。

定义3 路网轨迹。假设所有的移动对象均受到路网G的约束，那么通过路网匹配算法，轨迹数据可以通过路网结构进行表示，即路网轨迹τ=〈(e1,t1),(e2,t2),…,(er,tr)〉，其中：ei∈E表示轨迹在路网G中的某个路段，ti表示轨迹进入该路段ei时的时间戳。

与PRESS算法类似，将路网轨迹τ分别表示为空间方面的路段序列τs=〈e1,e2,…,en〉和时间序列τt=〈t1,t2,…,tn〉，通过两种完全不同的模型分别对轨迹数据进行压缩，以达到更高的压缩效率。在空间方面，不同于传统的基于最短路径的压缩方法，CTPM的压缩过程分为训练和压缩两个阶段。在训练阶段通过轨迹历史数据构建部分匹配预测(Prediction by Partial Matching， PPM)模型，通过轨迹已经行驶的部分路段对其下一时刻可能行驶的路段进行预测。在压缩阶段，利用生成的预测模型对轨迹下个可能的路段进行预测，若预测成功则将该路段删除，若预测失败则保留该路段信息，以减少轨迹数据的存储代价。在解压过程中，通过预测模型，将压缩后的轨迹完全还原，使其在空间上无损压缩。在时间方面，通过历史轨迹数据计算路网中不同时间区间下道路的通行速度，结合轨迹当前阶段的速度信息和道路长度信息，来计算轨迹时间信息，以此得到预测的轨迹时间序列，最后通过对比原始轨迹与预测轨迹之间时间的相似度来保留关键的时间变化路段，使得预测轨迹的满足一定误差阈值。下面，分别从空间和时间两个方面来详细地介绍本文方法。

2 空间轨迹压缩

将轨迹的空间信息表示为路段的序列，即τs=〈e1,e2,…,en〉。空间轨迹无损压缩的目的是通过预建的字典T将τs压缩为一个更短的序列。由于轨迹的长度、起点和终点具有随机性，传统的0阶区间编码算法如霍夫曼编码(Huffman Coding)、LZ系列算法等需要构建较大的字典树导致压缩比较低。然而轨迹数据由于受到交通状况的约束，其可能的行驶的路段往往依赖于之前行驶的路段。例如若车辆驶入高架路段，其行驶轨迹往往无法改变直到驶出该路段，因此利用具备k阶马尔可夫模型的PPM算法，通过轨迹已经行驶的部分路段来预测轨迹下一时刻可能行驶的位置。整个空间压缩过程可以分为两个阶段：一个是通过历史数据生成PPM预测模型；二是通过PPM模型对轨迹进行压缩。下面对PPM预测模型进行描述。

2.1 部分匹配预测模型(PPM)

Senft等[13]提出了一种基于前缀字典树的数据压缩(Suffix Tree based Data Compression, STDC)算法，该算法是PPM模型的一种实现，其主要思想是在输入序列中利用序列元素的顺序和频度来预测一下元素可能出现的概率。PPM需要指定待构造的变阶马尔可夫模型的阶数k，通过训练数据集构造一棵字典树T。若模型阶数为k，则PPM构造的字典树的最大深度为k+1。字典树T的每一个节点由一个两元组(c,num)构成，其中：c为训练序列中出现的元素，num为元素c出现的频度。字典树中的每一条从根节点到叶子节点的路径表示序列中的一个子序列，字典树的根节点不表示任何信息，表示一个空序列。在构造字典树的过程中，算法将训练序列分割成长度为k的子序列集合，依据子序列构造字典树结构，每一条路径为一个子序列。每个子序列会使得该路径下所有元素频度num+1。在构造完字典树之后，通过式(1)来计算序列s之后出现元素c的概率：

(1)

其中：序列s的长度为k-1；num(sc)为长度为k的序列sc出现的频度；Qs是以s为前缀的所有序列集合。

通过一个例子来说明PPM算法。假设输入序列为ACBAEADACBA，假设马尔可夫模型阶数k=3，则该序列会被划分为子序列集合ACB、CBA、AEA、EAD、ADA、ACB、CBA，其构建的字典树如图1所示。利用该字典树，可以通过式(1)来计算序列AC后出现B的概率为p(B|AC)=2/(1+2)=0.667。

2.2 基于预测的空间轨迹压缩算

通过大量的历史轨迹数据对PPM模型进行训练，利用训练好的PPM模型可以通过轨迹之前行驶的路段来预测轨迹下一个位置。PPM模型可以用式(2)表示：

ψ(τ,D)=arg maxP(st/τ′)

(2)

其中：τ为给定的待压缩的轨迹；D为历史轨迹数据集；τ′是轨迹τ中长度为k的子序列；st为τ′后的下一个路段。用字典树T表示PPM模型ψ，树中的每个节点node包含路段信息rid、孩子节点列表children、频度信息num和预测下一个可能的路段信息pred。

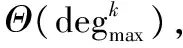
算法1 PPM训练算法。

输入：路网G，历史轨迹数据集D，模型阶数k。

输出：表示PPM模型的字典树T。

初始化字典树T

Foreachτ∈DDo

Foreachi← 0 to |τ| Do

/* 将轨迹段sti之前的k个路段作为滑动窗口*/

start←i

end← min(i+k,|τ|-1)

nd←T.root

Foreachj← [start,end] Do

/*滑动窗口路段构成的路径的频度+1*/

nd←nd.children[stj];

nd.children[stj+1]++;

/*选出频度最大的节点作为预测节点*/

nd.pred← max(nd.children[].num)

ReturnT

基于PPM模型的压缩算法实现的伪代码如算法2所示。算法将训练好的PPM模型的字典树T、轨迹τ和阶数k作为输入，输出一条压缩轨迹τ′。首先，算法将τ中的前k-1条路段加入压缩轨迹τ′中。从τ中第k条路段开始，将其前k-1条路段作为滑动窗口，找到该滑动窗口对于序列路径的最后一个节点，并判断该节点的预测结果nd.pred与第k条轨迹段sti是否一致，若预测错误，则将sti加入压缩轨迹τ′中，直到轨迹中所有的路段被处理完成。通过算法2可以对轨迹在空间上进行无损压缩，即对于任意一条压缩后的轨迹都可以通过算法1生成的字典树T将其还原。同时算法2具有较好的性能，其时间复杂度为Θ(|τ|·k)。

算法2 基于PPM模型的压缩算法。

输入：PPM模型T，待压缩的轨迹τ，模型阶数k。

输出：压缩后的轨迹τ′。

将轨迹τ中前k-1条路段加入τ′

Foreachi←kTo |τ| Do

/*将路段sti之前的k-1个路段作为滑动窗口*/

start← max(0,i-k),end←i-1;

nd←T.root.children[ststart];

While |end-start|>1 andnd.children[ststart+1] Do

start←start+1

nd←T.root.children[ststart]

/*当预测失败时，将该路段加入压缩轨迹*/

Ifnd.pred!=stiThen;

τ′ ←τ′∪sti;

Returnτ′

3 时间轨迹压缩

轨迹的时间信息表示为路段与时间的二元组序列，即τ=〈(e1,t1),(e2,t2),…,(en,tn)〉。对于一个路网G来说，往往可以很容易获得路网上任意一条路段e的路径长度，用d(e)来表示，因此可以通过轨迹的通行速度来计算轨迹的时间信息，即ti+1=ti+d(ei+1)/vi+1，其中：vi+1表示移动物体在路段ei+1时的通行速度，因此，时间轨迹压缩算法通过对历史轨迹数据进行统计，预测每条轨迹在各自路段的通行速度，从而得到预测的轨迹时间序列。通过对比预测轨迹与原始轨迹，将预测误差较大的时间点保留，将误差较小的时间点删除，以达到轨迹压缩的目的。轨迹的时间维度压缩会造成时间信息的损失，因此需要先对轨迹的时间距离进行度量。由于轨迹的空间信息压缩是无损的，只需要对比轨迹在各自路段上时间信息距离，其形式化定义如下。

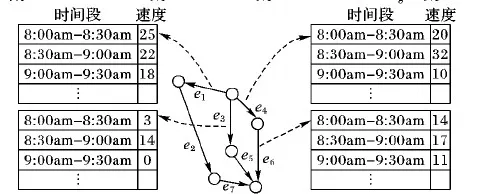
图2 时间相关的速度路网举例

算法3描述了算法实现的伪代码。算法的输入为原始轨迹τ、时间距离值θ、起始路段s和结束路段e，算法的输出为压缩轨迹τ′。算法首先获得起点为s终点为e的子轨迹段τs,e，通过预测速度得到该预测轨迹τs,e′。通过挨个寻找预测误差最大的路段，删除该路段后的原始轨迹τs,e和预测轨迹τs,e′的路网同步时间距离(Network Synchronized Time Difference, NSTD)最小。若删除后的NSTD仍然大于误差阈值θ，则将路段min作为分割点，将轨迹切割成两条子轨迹重新进行计算；否则说明子轨迹τs,e可以用预测轨迹τs,e′误差有界表示。算法的执行过程与Douglas-Peucker算法[14]相似，其时间复杂度为Θ(|D|·|τ|2)，其中：|τ|为轨迹平均路段数目，|D|为轨迹数据集D中的轨迹数。

算法3 时间信息压缩算法(Time-compression)。

输入：原始轨迹τ，时间距离阈值θ，起始路段s，结束路段e。

输出：压缩轨迹τ′。

τs,e=segmentation(τ,s,e)

根据速度得到预测轨迹τs,e′

min←start

/*选择删除预测轨迹中预测误差最大的路段*/

Foreachi←startToendDo

ti′ ←ti

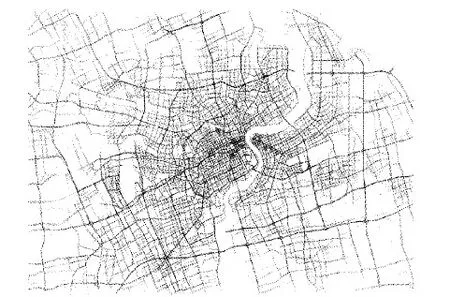
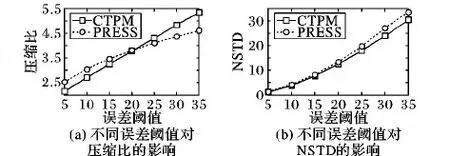
IfNSTD(τi,τi′)

min←i

dist←NSTD(τmin,τmin′)

Ifdist>θthen

Time-compression(τ,θ,s,min)

Time-compression(τ,θ,min,s)

Else

删除τ中s+1到e-1的轨迹段

将保留的轨迹段加入τ′

Returnτ′

4 实验结果与分析

通过一个真实轨迹数据集来验证压缩算法的有效性。实验所用的数据集为2016年4月1日上海市的出租车轨迹数据集，该数据集包含45 902条轨迹数据，其平均长度为5 692 m，平均采样率为15 s，数据集可视化情况如图3所示。实验使用Java编程语言实现所有的算法。所有实验的硬件平台均为Intel Core i5@3.2 GHz CPU和8 GB RAM的PC机，操作系统为64位Window 7系统，JDK版本为64位1.8.0 20。将轨迹的压缩比定义为原始轨迹τ和压缩轨迹τ′所需存储空间的比值，即c=|τ|/|τ′|，作为算法压缩性能的评价指标。

图3 轨迹数据集可视化

首先分析CTPM的空间轨迹压缩算法的有效性。CTPM在空间方面需要指定待构造的变阶马尔可夫模型的阶数k，图4展示了该参数对压缩效果的影响。如图4(a)所示，随着k值的增加，CTPM的压缩比先增加后降低；当k=2时，算法压缩比最高，其值为12.25。图4(b)展示了阶数k对压缩时间的影响，随着k值的增加，算法的匹配次数随之增加，所需要的压缩时间呈线性趋势增加。

图4 模型阶数k对压缩性能的影响

下面对比PRESS算法与CTPM在空间维度下压缩性能。PRESS算法与CTPM在空间方面均为无损压缩，两者的区别是PRESS算法通过使用最短路径算法来预测轨迹下一个位置，而CTPM通过对历史数据学习得到字典树来预测轨迹的下一个位置。将轨迹长度定义为一条轨迹包含轨迹段的数量，即|τ|。对于不同的轨迹长度，两种算法的压缩性能对比如图5(a)所示。由图5(a)可以看出，随着轨迹长度的增加，CTPM的压缩比也随之增加，而PRESS算法在轨迹长度为70时压缩性能与CTPM相似，二者压缩比均为6.2；当轨迹长度在70到110之间时，PRESS算法的压缩比随着轨迹长度的增加而增加；当轨迹长度超过110时，PRESS算法的压缩比明显降低。不同的轨迹数下，两种算法的压缩时间对比如图5(b)所示。由图5(b)可以看出，两者算法所需的压缩时间均随着轨迹数的增加而增加，但由于PRESS需要计算任意两个路段的最短路径，因此其需要的压缩时间明显高于CTPM。

图5 CTPM与PRESS算法空间压缩性能对比

PRESS算法与CTPM在时间维度下均为有损压缩，本文使用路网同步时间距离NSTD来度量原始轨迹与压缩轨迹之间的误差。不同的误差阈值下，两种算法的压缩性能对比如图6所示。由图6(a)可以看出，随着误差阈值的增加，两种算法的压缩比都随之增加；当误差阈值小于20时，PRESS算法的压缩比略高于CTPM；当误差阈值大于于20时，CTPM的压缩性能将优于PRESS算法。不同的误差阈值下，两种算平均路网同步时间距离NSTD的对比如图6(b)所示。由图6(b)可以看出，随着误差阈值的增加，两种算法的NSTD都随之增加。整体来看CTPM的误差略小于PRESS算法。

图6 CTPM与PRESS算法时间压缩性能对比

上述实验表明，在空间方面，CTPM通过采用PPM模型代替计算耗时、准确率较低的最短路径算法，将压缩的重点由静态的路网结构转换到动态的历史轨迹数据，在减少压缩时间的同时有效地提高了压缩比。在轨迹平均长度为70到200的数据集中，CTPM与PRESS算法相比压缩比提高了43%。在时间方面，CTPM通过采用速度预测模型有效地降低了平均压缩误差，在误差阈值5到35的参数设定下，CTPM与PRESS算法相比压缩比提高了1.5%，平均NSTD误差减小了9.5%。

5 结语

本文针对目前路网环境下轨迹数据压缩的问题，提出了一种基于预测模型的轨迹数据压缩方法(CTPM)。在空间维度预测轨迹下一个可能的位置,，在时间维度预测轨迹进入下一路段的时间，通过删除预测正确的信息以达到数据压缩的目的。本文通过真实的出租车轨迹数据集来验证算法的有效性，实验表明在空间方面，CTPM相对于传统的PRESS算法在降低压缩时间的同时大幅提高了压缩比。在时间方面，CTPM可以有效地减少有损压缩带来的误差。然而，周期性的速度模型无法很好地描述某些突发性的交通状况，如车祸、道路施工等导致的堵车现象。在后续的工作中，可以通过结合实时路况信息来提升轨迹到达时间预测的准确性，在时间维度进一步优化压缩性能。

References)

[1] 高强,张凤荔,王瑞锦,等.轨迹大数据:数据处理关键技术研究综述[J].软件学报,2017,28(4):959-992.(GAO Q, ZHANG F L, WANG R J, et al. Trajectory big data: a review of key technologies in data processing [J]. Journal of Software, 2017, 28(4): 959-992.)

[2] MUCKELL J, HWANG J H, PATIL V, et al. SQUISH: an online approach for GPS trajectory compression [C]// Proceedings of the 2011 International Conference on Computing for Geospatial Research & Applications. New York: ACM, 2011: 1-8.

[3] HASHEMI M, KARIMI H A. A critical review of real-time map-matching algorithms: current issues and future directions [J]. Computers Environment & Urban Systems, 2014, 48(8): 153-165.

[4] BRAKATSOULAS S, PFOSER D, SALAS R, et al. On map-matching vehicle tracking data [C]// Proceedings of the 2005 International Conference on Very Large Data Bases. [S.l.]: VLDB Endowment, 2005: 853-864.

[5] KELLARIS G, PELEKIS N, THEODORIDIS Y. Trajectory compression under network constraints [C]// Proceedings of the 2009 International Symposium on Spatial and Temporal Databases. Berlin: Springer, 2009: 392-398.

[6] CAO H, WOLFSON O. Nonmaterialized motion information in transport networks [C]// ICDT 2005: Proceedings of the 2005 International Conference on Database Theory, LNCS 3363. Berlin: Springer, 2005: 173-188.

[7] LERIN P M, YAMAMOTO D, TAKAHASHI N. Encoding travel traces by using road networks and routing algorithms [J]. International Journal of Knowledge and Web Intelligence, 2013, 4(1): 233-243.

[8] 张广林,胡小梅,柴剑飞,等.路径规划算法及其应用综述[J].现代机械,2011(5):85-90.(ZHANG G L, HU X M, CHAI J F, et al. Summary of path planning algorithm and its application [J]. Modern Machinery, 2011(5):85-90.)

[9] 张仁平,周庆忠,熊伟,等.A*算法改进算法及其应用[J].计算机系统应用,2009,18(9):98-100.(ZHANG R P, ZHOU Q Z, XIONG W, et al. Updated A*algorithm and its application [J]. Computer Systems & Applications, 2009, 18(9): 98-100.)

[10] KELLARIS G, PELEKIS N, THEODORIDIS Y. Trajectory compression under network constraints [C]// Proceedings of the 2009 International Symposium on Spatial and Temporal Databases. Berlin: Springer, 2009: 392-398.

[11] KELLARIS G, PELEKIS N, THEODORIDIS Y. Map-matched trajectory compression [J]. Journal of Systems & Software, 2013, 86(6): 1566-1579.

[12] SONG R, SUN W, ZHENG B, et al. PRESS: a novel framework of trajectory compression in road networks [J]. Proceedings of the VLDB Endowment, 2014, 7(9): 661-672.

[13] SENFT M. Suffix tree based data compression [C]// SOFSEM 2005: Proceedings of the 2005 International Conference on Current Trends in Theory and Practice of Computer Science, LNCS 3381. Berlin: Springer, 2005: 350-359.

[14] TIENAAH T, STEFANAKIS E, COLEMAN D. Contextual Douglas-Peucker simplification [J]. Geomatica, 2015, 69(3): 327-338.

CHENYu, born in 1972, M. S., senior engineer. His research interests include big data, artificial intelligence.

JIANGWei, born in 1990, M. S. His research interests include data management, data analysis.

ZHOUJi’en, born in 1976, Ph. D., senior engineer. His research interests include big data, artificial intelligence.