一种非合作目标模型快速测量方法
2018-03-20,,,*,
,,,*,
1. 北京控制工程研究所,北京 100190 2. 中国空间技术研究院,北京 100094
卫星在轨任务失败、燃料耗尽等都需要利用空间机械臂进行在轨服务来减少经济损失[1],目前,已完成的无人控制的技术验证任务都是针对合作目标。非合作目标的在轨服务仍然面临很多挑战,其中一个关键问题是如何精确获得动态自旋非合作目标的三维信息[2-3]。服务航天器跟踪、接近和捕获目标时,需要快速获取目标卫星局部模块的精密3D轮廓。
失效卫星一般处于高速自旋状态,常规激光成像雷达由于扫描间隔较长不适合高速动态目标;FLash Lidar 存在面阵小、分辨率低且器件难以获得的问题;双目视觉系统不适合对称、特征有限的目标,同名点匹配的效率和可靠性较低;编码结构光具有自动化程度高、速度快、精度高等特点,因此,编码结构光是当前一种非常有效的解决方案。
可以把结构光图像编码的方案分为3个类别[3]:顺序投影图案;彩虹或者色码投影;复杂的空间编码图案。文献[4]首先提出格雷码与相移法相结合的方法,解决了周期信号二义性问题,同时得到较高的空间分辨率,但是这种方法需要投影多幅图案,不能快速获取高速运动的非合作目标的三维轮廓。文献[5]提出一种彩色条纹自适应编码方法,但是采用彩色相机,对设备要求较高,复杂的空间环境加大了颜色分辨的难度,这种方法难以在轨实现。考虑到投影的图片数量只有一幅,文献[6]使用基于6值3次De Bruijn序列来生成水平彩色条纹图案,这种方法虽然可以满足快速性的要求,但是仍然采用彩色条纹,实现难度较大。
本文提出一种改进的De Bruijn序列编码方法,采用黑白单色条纹,可以快速进行条纹位置的定位,且不需要进行颜色分辨;基于极线约束原理,只需要对投影的行数或者列数进行编码;利用单目联合投影装置系统,在确定条纹边缘的过程中解码,不需要提前进行极线校正和畸变校正,直接重建出物体的三维信息。计算量较小,提高了重建速度。
1 相机和投影装置成像模型
图1为相机坐标系,由相机的小孔成像模型,利用投影关系,得到相机图像物理坐标系和相机坐标系之间的关系:
(1)
式中:(xc,yc)为像点在像平面坐标系中的坐标;fc为相机焦距;(Xc,Yc,Zc)为物方点在相机坐标系中的坐标。

图1 相机坐标系Fig.1 Camera coordinate system
投影装置的光线方向和相机的光线方向相反,把投影装置看作一个逆向的相机,采用和相机相同的物理模型来描述,得到投影装置图像物理坐标系和投影装置坐标系之间的关系:
(2)
式中:fp为投影装置焦距;(Xp,Yp,Zp)为物方点在投影装置坐标系中的坐标。
由于制造误差,相机和投影装置都具有畸变,在三维重建的过程中,为了使精度更高,需要对相机单元和投影装置单元进行畸变校正。畸变主要包括径向畸变和偏心畸变。
镜头径向畸变使像点沿径向产生偏差。径向畸变是对称的,对称中心与主点并不完全重合,但通常将主点视为对称中心。径向畸变有正有负,相对主点向外偏移为正,向内偏移为负。径向畸变可用奇次多项式表示:
Δr=K1r3+K2r5+K3r7+…
(3)
将其分解到像平面坐标系的x轴和y轴上,则有:
(4)

透镜组中心偏离主光轴而产生偏心畸变。偏心畸变使像点既产生径向偏差又产生切向偏差:
(5)
将其分解到像平面坐标系的x轴和y轴上,则有:
(6)
式中:P1、P2为偏心畸变系数。
综上所述,像点的系统性误差是径向畸变和偏心畸变引起的畸变总和:
(7)
对于单目结构光系统来说,重建系统的三维坐标,还需要知道相机和投影装置之间的位置和姿态。通过系统标定,已知相机和投影装置的外部参数分别为Rc和Rp,Tc和Tp,这两组外部参数都是以世界坐标系为基准的,整理可以得到投影装置坐标系和相机坐标系之间的关系:
(8)
得到物方点在投影装置坐标系和相机坐标系之间坐标的关系:
(9)
2 单目编码结构光快速方法
2.1 极线约束
在双目立体视觉中,极线几何对两个照相机平面的几何关系进行了讨论,投影装置的投射过程和相机的成像过程相反,因此可以把投影装置看作一个逆向的相机,采用和相机相同的物理模型来描述,照相机像平面和投影装置像平面也有相同的几何关系。考虑一点P,通过光学中心Op和OC分别在投影装置和照相机像平面上所成的像为P1和P2。这5个点都位于2条相交光线OpP和OCP所形成的外极平面上。特别地,P1位于该平面和投影装置像平面的交线l1上,直线l1是和点P相关联的外极线,它经过点e1。e1是连接两个光学中心Op和OC的基线和投影装置像平面的交点,同样,点P2位于与点P1关联的直线上,且该直线经过基线与照相机像平面的交点e2。当点P在极线l1和l2组成的平面上运动时,它在相机和投影装置像平面的投影仍落在极线l1和l2上。

图2 外极线约束Fig.2 Epipolar-slope constraint
如图2所示,点e1和e2称为两个摄像机的外极点[7,8],外极点e1是投影装置像平面中照相机的光学中心OC的投影,反之亦然。如上文所述,如果P1和P2是同一个点的不同像点,那么P1一定位于与P2相关联的外极线上。这就是立体几何中的外极线约束,通过这种约束,只能找到对应的外极线,不能找到对应点的具体位置。外极线约束把两幅图像上点之间的匹配关系从二维限制到一维,极大减小了搜索范围,是单目结构光系统三维重建的基础。在结构光编码的过程中,可以只对行数或者列数信息进行编码,减少了投影图片的数量。
2.2 黑白De Bruijn序列编码图案
结合上文所述的极线约束,投影图案只需要对行位置或者列位置进行编码,不需要采用空间网格编码的方式,相当于降低了编码的复杂性。空间的特殊复杂环境,比如表面反射率不均匀,能够从拍摄的图像中区分出不同像素单元灰度值、不同要求投影的编码图案灰度差较大,使得编码时条纹可以选择的灰度值数量较少。用有限的灰度值构造尽可能多不同的编码列数(或行数),选择De Bruijn序列编码。
De Bruijn序列是一种循环序列[9]。k个不同的字符,秩为n,可以排成长度为kn的字符串圆周,当绕这个圆周旋转一周时,长度为n将会出现kn个不同的单词,这个字符串圆周对应的序列称为基于k个符号的n次De Bruijn序列。图3是De Bruijn圆周的一个简单例子:n=3,k=2(字符为0和1)。当沿着这个圆周运动,将会依次遇到23=8个数字图案000,001,010,011,100,101,110,111每个只出现一次。在一定程度上,这个圆周非常有效的编码24位数字信息只用了8位[10]。在这个序列中,没有重复的三位数字图案。换句话说,任何一个序列都不可能和这个序列中其他序列对应。De Bruijn序列这个独特的特点可以用来重建条纹图案,每一个都有独特的形式图案彼此互不重复。这样的独特性让图案解码变得非常简单。
为了进一步提高编码对空间环境的适应性,可选元素中只选择黑白两种元素,在De Bruijn序列编码长度较长的情况下[11],要求编码次数较高,这就需要通过判断条纹宽度来解码,但是条纹宽度还受目标物体的形状影响,提高了解码的难度。
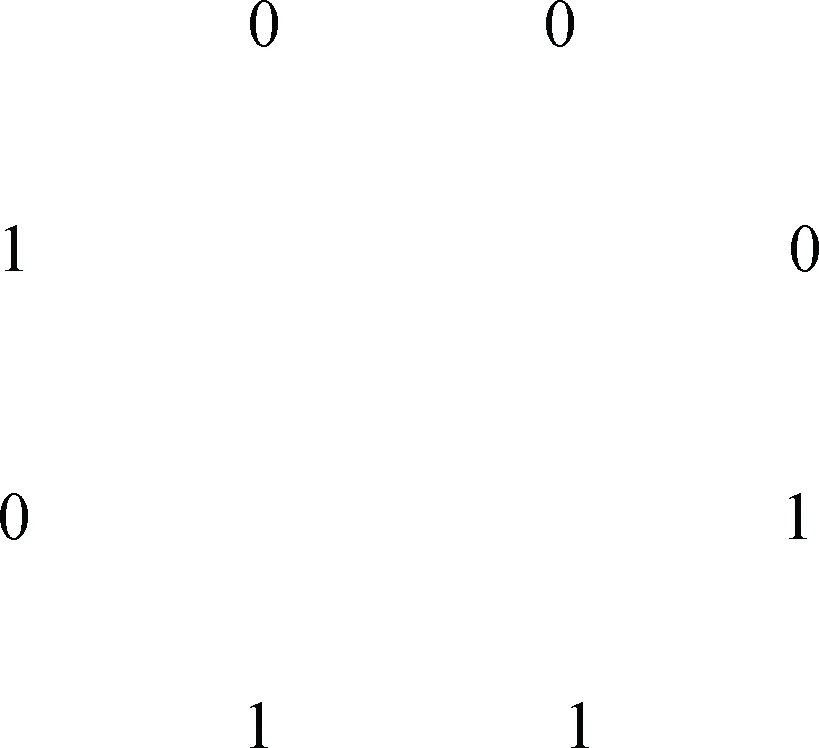
图3 n=3,k=2时的De Bruijn序列Fig.3 De Bruijn sequence
因此,本文提出一种方法,以两种不同比例的黑白条纹作为编码的基本单元,如图4所示,主要优点如下:
条纹模板中使用的颜色是黑色和白色,这样无需考虑摄像机和投影仪的颜色失真问题和颜色识别算法,算法复杂性降低,也不容易受到环境光或者待测物体表面颜色信息的影响,抗干扰能力增强;颜色的对比度高,后续解码的过程中条纹边缘更易检测;编码图案黑白条纹宽度之和是相等的,即条纹存在着规律性,降低了投影仪图案和相机图案匹配的难度。
采用图4所示的编码基本单元,利用2元3次De Bruijn序列,设计的编码图案如图5所示。该编码图案原理简单,易于实现,能够实现高精度稠密深度数据的获取。

图4 编码基本单元0和1Fig.4 Basic unit of coding

图5 黑白De Bruijn序列编码图案Fig.5 Black-and-white coding patterns of De Bruijn sequence
2.3 物体表面三维信息的计算
在解码的过程中,采用阈值法和灰度矩法确定条纹边缘的位置。
综合考虑式(1)(2)和(9),Xc、Yc、Zc、Xp、Yp、Zp和yp是未知的,而这三式中有7个线性无关的方程,联立这三式,可唯一地确定被测点在相机坐标系和投影装置坐标系中的三维坐标。
式(1)(2)中的xc、yc和xp需要进行畸变校正,相机物理像平面的坐标(xc,yc)校正根据校正公式(7)即可,根据畸变模型[12],畸变校正需要知道像素单元距离中心的距离,而我们只知道投影装置单元的列数信息,无法直接根据校正公式(7)进行畸变校正,本文提出一种多次迭代的方法进行投影装置单元校正。

(10)
(11)

3 试验结果
如图6所示,单目编码结构光系统采用单相机和投影装置的组合,相机的分辨率为2 048×2 448,投影装置的分辨率为912×1 140,待测目标位于系统前0.5 m左右。
考虑非合作目标三维轮廓测量的特殊要求,首先目标高速运动[13],要求测量时间短;其次为了进一步实现非合作目标的在轨服务,要求测量精度高;再次空间目标表面材料反射率不均匀,且经常伴有高光现象,不适合利用灰度值或颜色进行三维重建。

图6 系统实物Fig.6 Physical map of the system
首先应用平面靶标和标定平面完成相机和投影装置的标定[14-17],用Matlab生成上文提出的黑白De Bruijn序列编码图案,通过投影装置投射到待测目标上,附加编码图像的条纹由照相机同步进行拍摄,计算机对图片进行处理,通过单幅编码图案和图片就可以计算出物体表面的三维信息。针对白色海盗雕塑目标,得到的三维信息如图7所示(坐标系为投影装置坐标系,单位为mm)。

图7 白色海盗雕塑重建结果Fig.7 Reconstructed results of the sculpture
为了进一步验证这种方法可以应用于非合作目标的快速三维测量,以1∶6的卫星模型为重建目标,如图8(a)所示,图8(b)是测量过程中相机拍摄的图片,图9(a)是相机图片处理过程中的有效单元,可以看出金色的遮光材料导致的高光问题在一定程度上影响了重建结果。得到的三维信息如图9(b)所示,点云能够直接反应出卫星白色天线部分的结构。
利用此单目结构光系统对标准件进行测量,测得深度信息误差为0.058 3 mm,能够满足结构光测量系统的三维重建精度要求。
以上试验证明,系统使用高速相机,采集图像时间较短,单幅图像即可进行重建,同时只采用黑白单色条纹,在空间环境中抗干扰能力强,速度和精度都能满足非合作目标的三维测量要求。

图8 卫星模型实物与相机拍摄的附有投影编码的卫星模型Fig.8 Satellite model and photo with coding pattern by camera

图9 处理过程中和卫星模型的有效单元Fig.9 Effective unit during image processing and reconstructed results of satellite model
4 结束语
本文提出了一种改进的黑白De Bruijn序列编码方案,与传统的De Bruijn彩色条纹编码方案不同,采用黑白单色条纹,降低了对设备的要求,更能适应空间复杂的反射环境,同时保留了De Bruijn编码单幅图案就可以进行重建的优点;利用极线约束,只对行数或者列数进行编码,进一步降低了编码的复杂性;在单目编码结构光的测量过程中,应用文中提出的匹配重建算法,在确定条纹边缘的过程中进行解码,不需要事先进行极线校正;创新性地采用迭代的方法进行三维重建,在迭代的过程中对投影仪投影图片进行畸变校正,不需要对图片进行预处理,减少了计算量,同时提高了重建精度,算法更加简单,效率更高。试验结果表明采用这种方法,深度信息误差为0.058 3 mm,可以满足高速运动的非合作目标的三维测量要求。该方法可用于卫星局部模块3D轮廓的快速获取,帮助服务航天器快速有效地跟踪、接近和捕获目标。
References)
[1] NASA. On-orbit satellite servicing study,NASA 10-204001[R]. NASA Internal Project Report,2010.
[2] MARTIN D H,ANDERSON P R,BARTAMIAN L. Communication satellites[M]. 5th Edition. Reston:Aerospace Press Series,2007.
[3] YANG R,CHENG S,YANG W,et al. Robust and accurate surface measurement using structured light [J]. IEEE Trans. Instrumentation and Measurement,2008,57(6):1275-1280.
[4] BERGMANN D. New approach for automatic surface reconstruction with coded light[C]∥Proceedings of Remote Sensing and Reconstruction for Three- Dimensional Objects and Scenes,SPIE,San Diego,CA,1995,2572:2-9.
[5] THOMAS P KONINCKX,LUC VAN GOOL. Real-time range acquisition by adaptive structured light[J]. IEEE Trans. Pattern Analysis and Machine Intelligence,2006,28(3):432-445.
[6] DAVID A. FORSYTH,JEAN PONCE.计算机视觉:一种现代方法[M].北京:电子工业出版社,2004:6.
[7] 赵慧洁,雷炎章,姜宏志.基于投影栅相位的立体匹配方法[C]∥第十三届图形图像会议论文集,2006:496-500.
ZHAO H J,LEI Y Z,JIANG H Z. Depth measurement based on projected grating phrase[C]∥,2006:496-500(in Chinese).
[8] 关芳芳,程筱胜. 基于极线校正的相移结构光三维测量[J]. 南京工程学院学报(自然科学版),2014,6(9):37-45.
GUAN F F,CHENG X S. Three-dimensional structured-light measurement based on epipolar-slope constraint[J]. Journal of Nanjing Institute of Technology (Natural Science Edition),2014,6(9):37-45(in Chinese).
[9] JASON G. DLP-based structured light 3D imaging techno-logies and applications[C]∥SPIE MOEMS-MEMS,Inter-national Society for Optics and Photonics,2011,7932:10.
[10] 陈石平,毕娅,李晓星,等. 亚像素条纹边缘提取技术在型面测量上的应用[J]. 北京航空航天大学学报,2006,32(8):94-101.
CHEN S P,BI Y,LI X X,et al. The technique of sub-pixel stripes distinguish on the surface measurement[J]. Journal of Beijing University of Aeronautics and Astronautics,2006,32(8): 94-101(in Chinese).
[11] 陈彦军. 基于编码结构光的三维重建关键技术研究[D]. 哈尔滨:哈尔滨工业大学,2012.
CHEN Y J. Research on key technologies for 3D Reconstruction based on coded structured light[D]. Harbin:Harbin Institute of Technology,2012(in Chinese).
[12] 李明磊,高欣圆,李广云,等. 地面三维激光扫描仪与外架数码相机间安置参数的高精度标定[J]. 光学精密工程,2016,24(9):2158-2166.
LI M L,GAO X Y,LI G Y,et al. High accuracy calibration of installation parameters between 3D terrestrial laser scanner and external-installed digital camera[J]. Optics and Precision Engineering,2016,24(9):2158-2166(in Chinese).
[13] 于洋,王世勇,蹇毅,等. 面阵探测器连续扫描成像光学系统[J]. 红外与激光工程, 2016,45(S4):120-126.
YU Y,WANG S Y,JIAN Y,et al. Realization of an optical system based on continuous-scan focal plane array[J]. Infrared and Laser Engineering,2016,45(S4):120-126(in Chinese).
[14] 梁斌,高学海,徐文福. 基于结构光的空间大目标特征重构与位姿测量[J]. 中国空间科学技术,2014, 34 (5):24-31.
LIANG B,GAO X H,XU W F,et al. Feature Reconstruction and pose determination for large space target based on point structured light[J]. Chinese Space Science and Technology,2014,34 (5): 24-31(in Chinese).
[15] ZHOU F,ZHANG G. Complete calibration of a struc-tured light vision sensor through planar target of unknown orientations[J].Image and Vision Computing,2005,23(1):59-67.
[16] YANG R Q,WEI S C,CHEN Y Z,et al. Robust and accurate surface measurement using structured light[J]. IEEE Tans. Instrumentation and Measurement,2008,57(6):1275-1280.
[17] CHEN Y J,WANG K Q,ZUO W N,et al. Coded structured light stripe boundary location with sub-pixel accuracy based on weighted centroid method[J]. Journal of Biological Systems,2010,1(18):35-49.
