基于X射线脉冲星导航试验卫星观测数据的到达时间估计

，，，，，，，，，，

1. 钱学森空间技术实验室，北京 100094 2. 中国空间技术研究院，北京 100094

脉冲星是存在于宇宙中的一种高速运转的中子星，因自身极其稳定的周期性而被誉为宇宙中最稳定的天文时钟，尤其是毫秒脉冲星的周期稳定度可达到10-19～10-21s/s[1，2]。X射线脉冲星导航(X-ray Pulsar-based Navigation，XPNAV)是利用脉冲星辐射的X射线进行导航[3-5]的一种新概念导航技术，它是利用X射线频段的计时观测数据，通过差分方程自主确定航天器的导航参数。X射线脉冲星导航系统对于未来导航系统的发展具有重要的研究意义，近年来备受国内外学者的广泛关注[6-8]。

2016年11月10日，中国首颗X射线脉冲星导航试验卫星-1(X-ray Pulsar-based Navigation-1,XPNAV-1)成功发射。XPNAV-1卫星工作在500 km的LEO轨道，是一颗质量为270 kg的小卫星。该卫星搭载了两种不同体制的X射线探测器——掠入射Wolter-I聚焦型X射线探测器(简称Wolter-I探测器)和准直型微通道板(Microchannel Plates，MCP)探测器(简称MCP探测器)。XPNAV-1卫星主要任务是在轨开展X射线脉冲星的探测并进行脉冲星导航体制的验证[9，10]。在前期的观测中，选择了蟹状星云(Crab)脉冲星(PSR B0531+21)[11]进行观测，目前已经完成了Wolter-I探测器对Crab脉冲星的多次观测，得到了Crab脉冲星辐射的一系列的X射线光子。

在X射线脉冲星导航系统中，脉冲星的脉冲到达时间(TOA)作为导航系统的基本观测量，其测量精度是后续的导航定位精度的决定性因素，因此对脉冲TOA进行高精度的求解是XPNAV系统中一个非常关键的问题[12]。多重信号子空间分类(Multiple Signal Classification，MUSIC)算法是阵列信号处理领域的一种高精度算法，主要是用于信号波达方向的估计，为了进行高精度的到达时间(Time Of Arrival，TOA)估计，本文提出了利用MUSIC方法，通过对接收数据的预处理，完成脉冲星导航系统中的TOA估计。为了验证方法的性能，对提出的方法进行试验仿真，即对Wolter-I探测器观测得到的X射线光子进行了光子折叠轮廓处理得到折叠轮廓，利用本文的方法，成功得到了折叠轮廓的TOA估计值，并且估计精度与传统互相关法相当。

1 脉冲轮廓

标准轮廓是脉冲星的一个重要特征，它是通过对脉冲星进行长时间观测，将得到的X射线光子TOA通过光子历元折叠方法得到的。不同脉冲星的标准脉冲轮廓不同，因此可以将脉冲星的标准脉冲轮廓作为XPNAV系统的一个必备数据。

图1是Crab脉冲星的标准轮廓[13]，表明了Crab脉冲星的一个重要特征，它是利用长时间多次观测的数据建立的。在XPNAV-1的观测中，截取了一段时间内的观测数据进行光子历元折叠。观测时间选为UTC 57 727.0约简儒略日(Modified Julian Day，MJD)到UTC 57 812.0 MJD，在0.5～10 keV频段内Wolter-I探测器共接收到4 853 983个光子，得到了119段PSR B0531+21的光子数据，将每段光子数据进行轮廓折叠[14，15]，可以得到一系列的脉冲折叠轮廓。随机选取8段时间内光子数据进行脉冲折叠轮廓，得到图2。

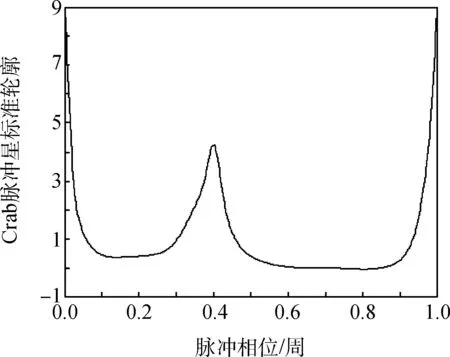
图1 Crab脉冲星标准轮廓Fig.1 Standard profile of Crab pulsar

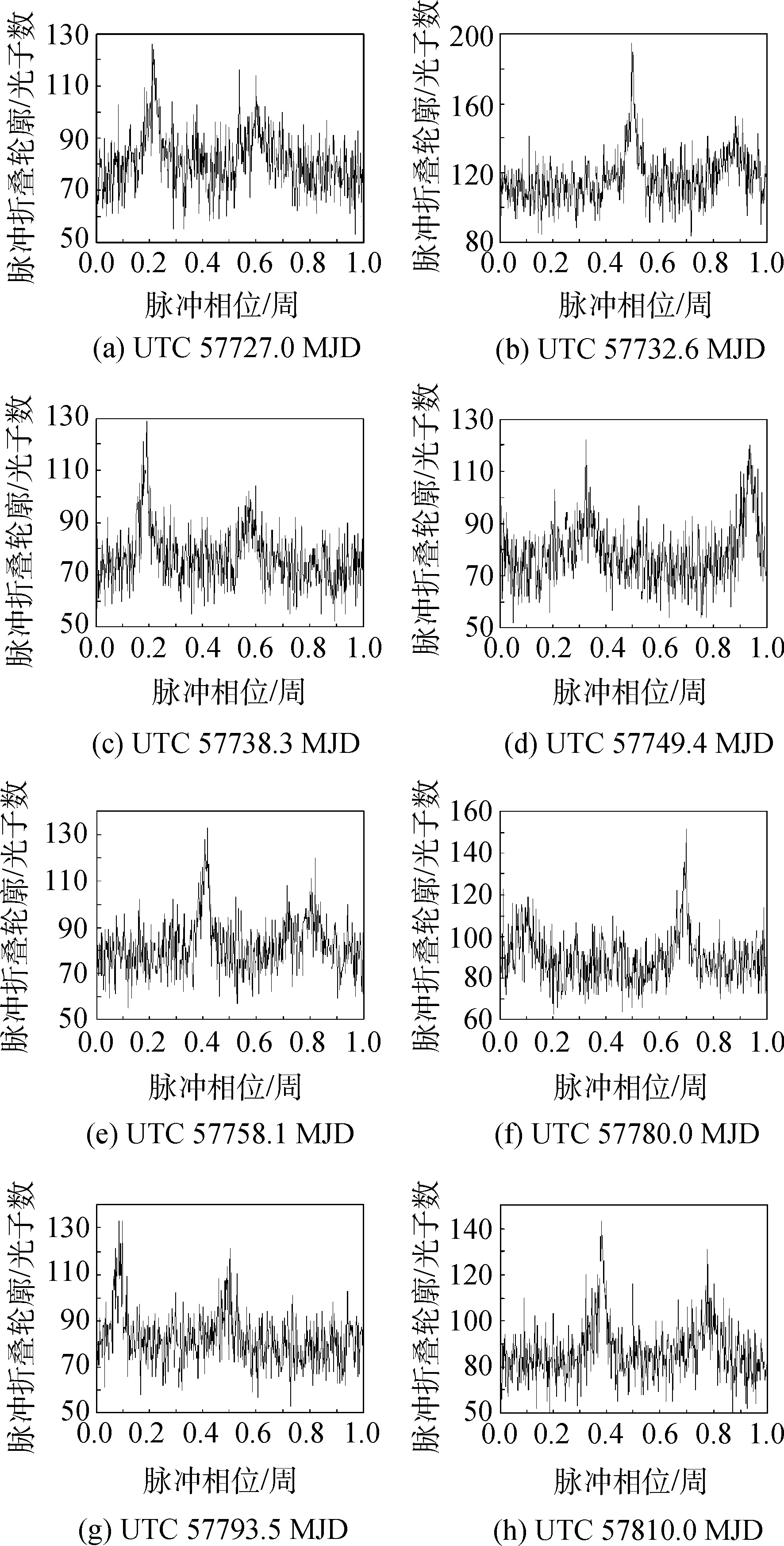
图2 Crab脉冲星折叠轮廓Fig.2 Epoch folding profiles of Crab pulsar

对比图1和图2，图2八段时间的观测轮廓与标准脉冲轮廓形状相同，但是在横坐标(即脉冲相位)存在着时间的左右偏离，时间偏离值称为脉冲TOA。脉冲TOA与相位之间的关系为TOA=φT0，T0为脉冲周期。

因此对于Crab脉冲星，可以定义其标准轮廓为s，观测得到的折叠轮廓为r，两者之间的关系可以建立为：

r(φi)=βs(φi-φ0)+ω(φi)

(1)

式中：β为幅度因子；φ0为r相对于s的相位偏离，即为待估计的TOA；φi(i=1,2,…,Nb)为第i个格对应的相位；Nb为在轮廓折叠过程中，将一个相位周期均匀划分的格数；ω(φi)为等效的折叠噪声，在折叠格中的光子数多于20个时，该噪声可以认为是均值为零的高斯噪声[16]。

2 脉冲TOA估计

在X射线脉冲星导航中，利用航天器上的X射线探测器探测到脉冲星X射线光子数据，通过对比脉冲星的同一个脉冲到达航天器与基准点之间的相位差，得到后续的导航参数。基准点可以设置在太阳系质心，通过脉冲星的计时观测模型可以得到基准点的TOA，而航天器处脉冲TOA需要利用互相关法、本文方法等获取。

2.1 互相关法

互相关法是TOA估计的常用方法，其基本原理在于对互相关函数最大值所对应的自变量的求解。

在用于XPNAV系统中进行脉冲TOA估计时，首先需要计算标准轮廓与折叠轮廓的互相关函数，即

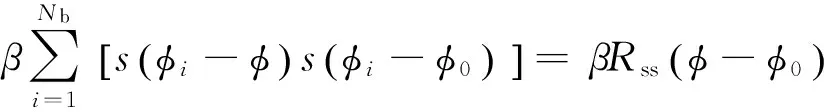
(2)

由自相关函数的性质：

|Rss(φ-φ0)|≤Rss(0)

(3)

因此，在Rsr(φ)在φ=φ0处有一个峰值，峰值对应处即为脉冲TOA的估计：

(4)

式中：arg{·}表示取函数的自变量；max[·]表示取函数的最大值。互相关函数的峰值点对应的延迟量即为脉冲TOA的估计。

2.2 本文方法

互相关法的计算简单，但XPNAV系统中，估计精度受噪声及信号形式的影响较大，因此针对XPNAV系统，本文提出了利用MUSIC算法对TOA进行估计。

2.2.1 MUSIC算法原理

MUSIC算法[17，18]具有“超分辨、高精度”的性能，基本原理是将接收的数据进行特征值分解，分解后得到两个相互正交的空间，利用两个空间的正交性计算出尖锐的谱峰，谱峰所对应的参数即为需要估计的参数。

首先可以将MUSIC算法的接收信号模型建立为：

X(t)=A(θ)S(t)+N(t)

(5)

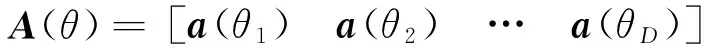
计算协方差矩阵:

R=E[XXH]=AE[SSH]AH+σ2I=

ARSAH+σ2I

(6)

对协方差矩阵进行特征值分解，可以得到特征值和对应的特征向量。将特征值由大到小排序λ1>λ2>…>λM，将特征值分为两部分，D个较大的特征值λ1,…,λD对应着信号，相应的特征向量u1,…,uD构成了信号子空间US=[u1,…,uD]；(M-D)个较小的特征值对应着噪声，相应的特征向量uD+1,…,uM构成了噪声子空间UN=[uD+1,…,uM]，假设噪声为高斯白噪声，那么有λD+1≈…≈λM≈0。

由MUSIC算法的性质[17]可知，US与UN正交，并且导向矢量阵A(θ)与US张成了同一空间，因此有：

(7)

式(7)等号右侧为一个零向量，表明阵列的导向矢量阵与噪声子空间是相互正交的。但是在实际环境中，式(7)的右侧并不是一个严格的零向量，而是近似为零向量。因此，MUSIC算法可以利用此性质来进行参数估计，即谱估计公式为：

(8)

最后，搜索PMUSIC(θk)的极大值点即为对应的参数值。

2.2.2 TOA估计

在波达方向(Direction-Of-Arrival，DOA)估计领域，MUSIC算法因其“高精度”性能备受学者的青睐。为了利用这个性质，本文将该算法引入到脉冲星导航系统中的TOA估计。

观察MUSIC算法的步骤可知，MUSIC算法进行DOA估计时，利用的是同一个接收时间下的不同阵元之间的接收数据进行信号参数的估计。而利用X射线光子探测器(Wolter-I探测器)接收到的光子数据并不是同一个接收时间下的不同阵元之间的接收数据，而是在同一个阵元的不同接收时间下的光子数据，并不符合MUSIC算法的信号模型，为此需要将光子数据进行整合处理。

利用一个X射线光子探测器(Wolter-I探测器)，在不同时间下得到光子到达时间的标记，然后进行脉冲轮廓折叠，可以得到式(1)的形式，将其写成矩阵形式为：

r= [r(φ1)r(φ2) …r(φNb)]T=

A(φ0)·β+ω

(9)

式中：r为观测的折叠轮廓矢量；A(φ0)=[s(φ1-φ0)s(φ2-φ0)…s(φNb-φ0)]T为导向矢量，是一个与φ0(即脉冲TOA)有关的矢量；ω=[ω(φ1)ω(φ2)…ω(φNb)]T为噪声矢量。

式(9)与式(5)具有相同的组成形式，因此可以考虑通过MUSIC算法来求解TOA。具体步骤为：

1)计算r的协方差矩阵Rr=E[rrH]；

2)对Rr进行特征值分解，UN=[u2,…,uNb]；

3)计算谱函数：

(10)

其中，搜索向量构造为：

A(φi)=[s(φ1-φi)s(φ2-φi)s(φNb-φi)]T

(11)

4)对f=[f(φ1),f(φ2),…,f(φNb)]的最大值进行搜索，最大值所对应的φk即为脉冲相位的估计，即：

(12)

3 TOA估计结果及分析

3.1 仿真及结果分析

首先对算法的有效性进行仿真，选取PSR B0531+21(即Crab脉冲星)为观测脉冲星，Crab脉冲星的周期为0.033 1 s，背景流量为5×10-3ph/s/cm2，来自脉冲星的流量为1.54 ph/s/cm2(流量参数统计频段为2 keV至10 keV内单位时间、单位面积探测器接收的光子数)。

(1)仿真1 TOA估计谱

选取Crab脉冲星为观测脉冲星，探测器的面积为0.5 m2，时间分辨率为100 μs，观测周期起点为57 727.0 MJD，观测周期长为0.5 s，起点脉冲相位设置为φ0=0.7，分别利用互相关和本文方法进行一次脉冲相位估计，并进行归一化处理，得到图3。

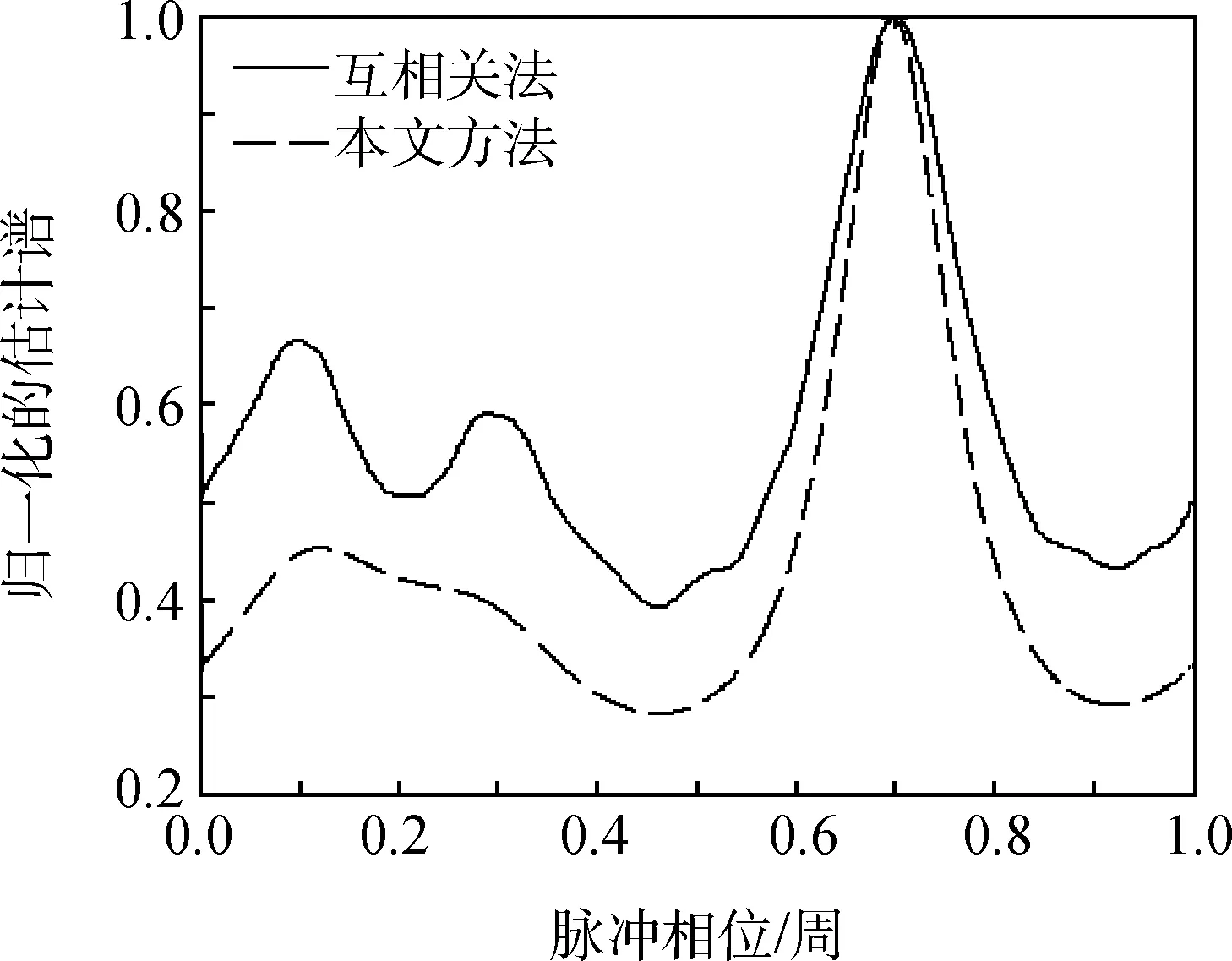
图3 TOA估计谱Fig.3 TOA estimation spectrum

由图3可知，本文方法的估计谱要比互相关方法的估计谱尖锐，对谱峰进行搜索，得到了互相关法与本文方法的TOA估计值分别为0.683 1和0.691 2，即本文方法的估计值较为准确。

(2)仿真2 不同观测时间下TOA估计误差

为了进一步验证算法的性能，观测时间选取0.1 s，0.2 s，0.5 s，1 s，5 s，10 s，20 s，50 s，在不同的观测时间下分别进行100次Monte-Carlo仿真，计算TOA估计的均方根误差，其他参数与仿真1相同。

图4为不同观测时间下的TOA估计误差，可以看到，观测时间越长，估计误差越小，即估计精度变高，而在相同的观测时间下，本文方法的估计精度要高于互相关法。

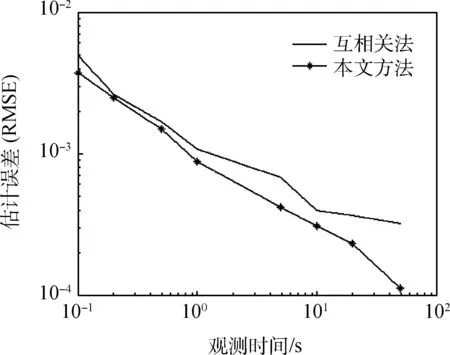
图4 不同观测时间下的TOA估计误差Fig.4 RMSE in different observation time

3.2 实测数据分析

图2是随机选取的8段光子数据进行脉冲折叠轮廓图，下面对这8段数据分别利用互相关法和本文方法进行脉冲相位的估计，将两种方法得到的估计谱进行归一化处理并进行比较，得到图5。

由图5可知，互相关法和本文方法均能得到TOA估计的谱峰，即两种方法都成功进行了TOA估计。对比两者的估计谱，可以明显看出前者的谱峰要比后者的尖锐，因此本文算法的估计结果较为精确。

最后统计8段数据的光子数和利用两种方法估计得到的脉冲相位，如表1所示。由表1的结果可以看出，本文方法与互相关法的估计结果相当。

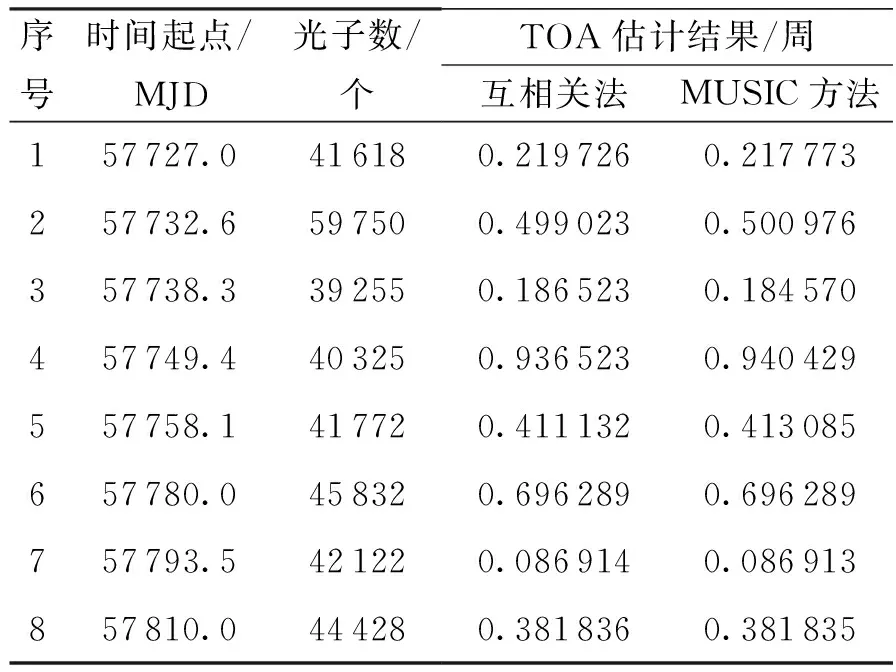
序号时间起点/MJD光子数/个TOA估计结果/周互相关法MUSIC方法157727.0416180.2197260.217773257732.6597500.4990230.500976357738.3392550.1865230.184570457749.4403250.9365230.940429557758.1417720.4111320.413085657780.0458320.6962890.696289757793.5421220.0869140.086913857810.0444280.3818360.381835

4 结束语

为了进行TOA估计，本文提出了利用MSUIC算法的高精度性质进行脉冲星导航系统中的TOA估计，并且对互相关法和本文方法进行了对比。仿真结果表明，本文方法的TOA估计的谱峰要比互相关法尖锐，在相同的情况下，本文方法的估计精度要高于互相关法。在XPNAV-1卫星前期的观测中，选取了光子流量较强的Crab脉冲星，卫星所搭载的探测器成功接收到了Crab脉冲星的光子数据，本文中选取了57 727.0 MJD到57812.0 MJD内0.5～10 keV频段内的光子观测数据进行处理，得到了脉冲轮廓折叠。XPNAV-1卫星的成功发射，对建立X射线脉冲星导航系统具有突破性的意义。在XPNAV-1卫星后续的任务中，我们也规划了对其他光子强度较弱的脉冲星的观测。

References)

[1] 帅平.脉冲星:宇宙航行的灯塔[D]. 北京：国防工业出版社，2016.

SHUAI P. Pulsar are lighthouses for space flight[M]. Beijing： National Defense Industry Press，2016(in Chinese).

[2] HEWISH A，BELL S J，PILKINGTON D H，et al. Obser-vation of a rapidly pulsating radio source[J]. Nature，1968，217：709-713.

[3] HANSON J E. Principles of X-ray navigation[D]. CA：Stanford University，1996：1-32.

[4] SHEIKH S I. The use of variable celestial X-ray sources for spacecraft navigation[D]. MD：Maryland University，2005：375-403.

[5] 帅平，陈绍龙，吴一帆，等. X射线脉冲星导航原理[J].宇航学报，2007，28(6): 1538-1543.

SHUAI P，CHEN S L，WU Y F，et al. Navigation principles using X-ray pulsars[J]. Journal of Astronautics，2007，28(6)：1538-1543(in Chinese).

[6] The ATNF Pulsar Catalogue[EB/OL].[2017-03-17].http:∥www.atnf.csiro.au/research/pulsar/psrcat.

[7] XIONG Z，QIAO L，KIU J Y，et al. GEO satellite autonomous navigation using X-ray pulsar navigation and GNSS measurements[J]. International Journal of Innovative Computing，Information and Control，2012，8(5): 2965-2977.

[8] ANDESON K D，PINES D J. Method of pulse phase tracking for X-ray pulsar based spacecraft navigation using low flux pulsars[C]. Space Ops. Conferences，Pasadena，CA，5-9 May，2014.

[9] 黄良伟，帅平，林晴晴，等. X 射线脉冲星导航标称数据库构建[J].中国空间科学技术，2015，32(3)：66-74.

HUANG L W，SHUAI P，LIN Q Q，et al. Research of the nominal database for X-ray pulsar navigation[J]. Chinese Space Science andTechnology，2015，35(3)：66-74(in Chinese).

[10] 黄良伟，帅平，张新源，等. 脉冲星导航试验卫星时间数据分析与脉冲轮廓恢复[J]. 中国空间科学技术，2017，37(3)：1-10.

HUANG L W，SHUAI P，ZHANG X Y，et al. XPNAV-1 Satellite timing data analysis and pulse profile recovery[J]. Chinese Space Science and Technology，2017，37(3)：1-10(in Chinese).

[11] WINTERNITZ L M，HASSOUNEH M，MITCELL J W，et al. X-ray navigation algorithms and testbed for SEXTANT[C]. IEEE Aerospace conference，2015:1-14.

[12] 林晴晴，帅平，黄良伟，等. 一种高精度的X射线脉冲星导航TOA估计方法[J].宇航学报，2016，37(6):604-701.

LIN Q Q，SHUAI P，HUANG L W，et al. A high precision TOA estimation method for X-ray pulsar-based navigation system[J]. Journal of Astronautic，2016，37(6):604-701(in Chinese).

[13] MPIfR EPN Pulsar Profiles Database，2017，available: http:∥rian.kharkov.ua/decameter/EPN/browser.html.

[14] EMADZADEH A A，SPEYER J L. X-ray pulsar-based relative navigation using epoch folding[J]. IEEE Transactions on Aerospace and Electronic Systems，2011，47(4): 2317-2328.

[15] EMADZADEH A A，SPEYER J L. On modeling and pulse phase estimation of X-ray pulsars[J]. IEEE Transactions on Signal Processing，2010，58(9)：4484-4495.

[16] HANSON J E，SHEIKH S I，GRAVEN P，et al. Noise analysis for X-ray navigation systems[C]. 2008 IEEE/ION Position Location and Navigation Symposium，Monterey，CA，May，2008.

[17] SCHMIDT R O. Multiple emitter location and spectrum estimation[J]. IEEE Transactions on Signal Processing，1986，34(3): 276-280.

[18] JIN H，SWAMY M N S，AHMAD M O. Efficient appli-cation of MUSIC algorithm under the coexistence of far-field and near-field sources[J]. IEEE Transactions on Signal Processing，2012，58(1): 2066-2070.