求解混合流水车间调度的多目标优化算法

谢 光，潘玉霞，李俊青

(1.三亚学院 信息与智能工程学院，海南 三亚 572000；2.聊城大学 计算机学院，山东 聊城 252059；3.东北大学 流程工业自动化国家重点实验室，辽宁 沈阳 110819)

0 引 言

混合流水车间调度(hybrid flow shop，HFS)作为经典流水车间调度问题的扩展，属于一类NP-难调度问题[1]。近年来，智能优化算法在求解HFS调度问题中得到了广泛应用，其中包括蚁群优化方法[1]、分布估计算法(estimation of distribution algorithm，EDA)[2,3]、粒子群优化算法(particle swarm optimization，PSO)[4]、迁徙鸟群优化算法(migrating birds optimization，MBO)[5]、人工蜂群算法[6,7]、布谷鸟群搜索算法(cuckoo search algorithm，CSA)[8]、生物地理学优化算法[9]等。上述文献中涉及的优化算法，有的全局搜索能力强但局部搜索能力弱，有的则反之。如何有效地平衡算法全局和局部搜索能力，亟待有效解决。算法混合可以有效提高算法性能，已成为相关研究热点。通过混合不同优化算法，或者优化算法与局部搜索算法相结合，可以在一定程度提升单一优化算法的性能。通过算法混合求解多阶段HFS问题的典型文献包括：人工免疫和蚁群优化混合算法[10]、蚁群优化和遗传混合算法[11]、迭代局部搜索和迭代贪心算法混合[12]、人工蜂群算法和禁忌算法混合[13]等。然而，综合考虑HFS调度问题的多目标特点，采用群体智能优化算法，构建一种多目标算法框架，目前相关研究还很少，亟待开展深入研究。

多目标优化算法在工业生产实际中得到了广泛应用和研究，目前主要有两种典型的多目标优化算法，即基于Pareto占优[14]和基本分解策略[15]。多目标优化与演化算法的融合也成为研究热点，如基于差分进化的多目标[16,17]、免疫多目标[18]、文化多目标[19]等算法。目前，在实际工业生产中，特别是钢铁生产调度过程中，处理多目标的技术以加权求和方法为主。上述方法一次运行只能得到一个解，且权重系数不好确定。仅有少量文献针对HFS调度问题开展多目标优化算法研究。譬如，采用NSGA-II求解炼钢生产HFS调度问题[20]，以及采用MOEA/D求解炼钢连铸集成计划问题[21]等。文献[22]针对近年来生产制造中的多目标优化算法进行分析。从文献可见，目前尚缺乏针对HFS调度问题的多目标优化算法。

鉴于此，本文提出了一种改进的MOEA/D优化算法，用于求解多目标HFS调度问题，主要贡献在于：①设计了两种局部搜索策略，特别是基于关键路径的强化局部搜索策略，可以有效提高算法求解性能；②设计了一种全局搜索交叉算子；③设计了一种种群更新策略，可以有效提高算法解的分布均匀性；④最小化3个目标，即最大完工时间目标，提前惩罚量和滞后惩罚量。

1 算法框架

1.1 编码和解码

HFS调度问题的定义和模型请参见文献[12,13]。采用简单工序排列编码方式[5,6]，即按照工件编号进行排列的编码方式。譬如，给定一个编码{1,2,3,7,8,9,4,5,6}，其对应的含义为：在第一个加工阶段，按照各工件在解中的位置次序先后调度，首先调度工件J1，之后J2，最后调度工件J6。进入下一个加工阶段后，工件按照在上一个加工阶段的完工时间从小到大进行排列，按照先来先服务的策略安排工件在下一个加工阶段加工。

1.2 种群初始化

初始化策略采用随机方法[13]，即随机生成PS个互不相同的初始解。

1.3 局部搜索策略

1.3.1 变异算子

针对采用基于排列编码的解，常采用的邻域生成策略主要有交换邻域、插入邻域等[5,6]。不同的邻域结构具备不同的挖掘和搜索能力，对于全局搜索和局部搜索的贡献则不同。本文采用随机选择交换邻域和插入邻域的策略，即产生一个新解时，随机选择交换邻域和插入邻域的一种作为变异操作算子。

1.3.2 基于关键路径的强化局部搜索策略

基于文献[26]给出的关键路径规则，设计基于关键路径的强化局部搜索策略，描述如下：

步骤1 针对当前解，划分加工关键块，即，每个关键块中的工件处于关键路径上。

步骤2 随机选择处于关键块中的两个工件编号，判断是否符合缩减邻域的条件之一，若符合，则按照缩减邻域规则，执行插入操作；否则，结束本次局部搜索，保持当前解不变。

1.4 全局搜索策略

为保证交叉操作的学习性和多样性，本算法给出了一种改进的交叉操作算子，具体描述如下：

步骤1 随机选择两个父代个体p1和p2，并随机选择两个位置r1和r2；

步骤2 填充两个子代个体c1和c2，使得它们在位置[r1,r2]部分的元素分别取自于p2和p1的对应位置；

步骤3 填充子代个体c1剩余部分，填充规则为：依次遍历父代个体p1的所有元素，若该元素尚未在子代个体c1中出现，则填充到第一个空白位置；子代个体c2剩余部分的填充规则与上述步骤相同。

交叉算子的示例如图1所示。

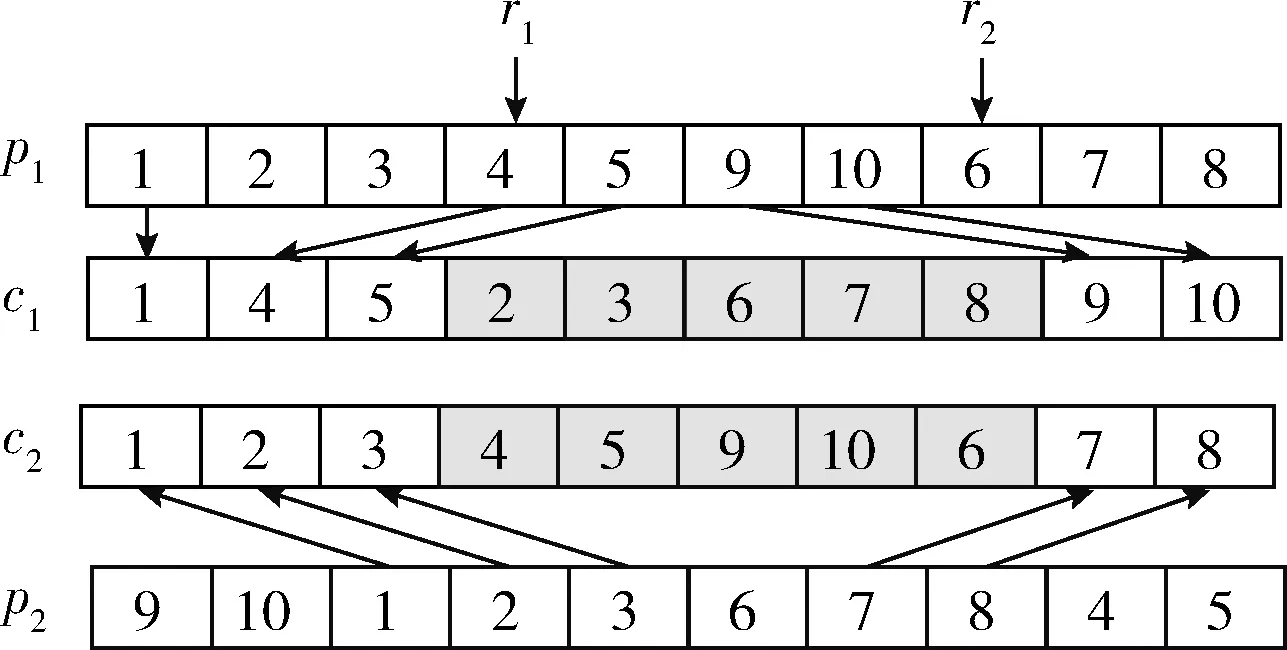
图1 交叉算子

1.5 多目标改进策略

1.5.1 权重向量生成策略

1.5.2 种群更新策略

当生成的子代个体加入下一代种群后，种群的大小会发生变化，为保持种群规模不变，需要淘汰劣解。淘汰解的策略在多目标优化算法中是一个研究热点。基于PBI值的大小是一种比较经典的策略[23]。然而，上述策略并不能保证一定保留Pareto较优解。譬如，图2给出了在给定的权重向量区域下，两个候选解x4和x5所在的位置，图中可见x4的PBI值大于x5的PBI值，因而，保留x5。然而，按照Pareto分层策略，x4相比x5具备更低的Pareto层，因而应保留Pareto较优解x4。基于上述分析，本文采用Pareto分层和PBI值比较相结合的策略，给出了一种新的种群更新策略，步骤如下：

步骤1 分别计算候选解的PBI值和Pareto层级；

步骤2 若两个候选解处于相同Pareto层级，则保留PBI值较小者；若候选解处于不同Pareto层级，则选择层级较小者。

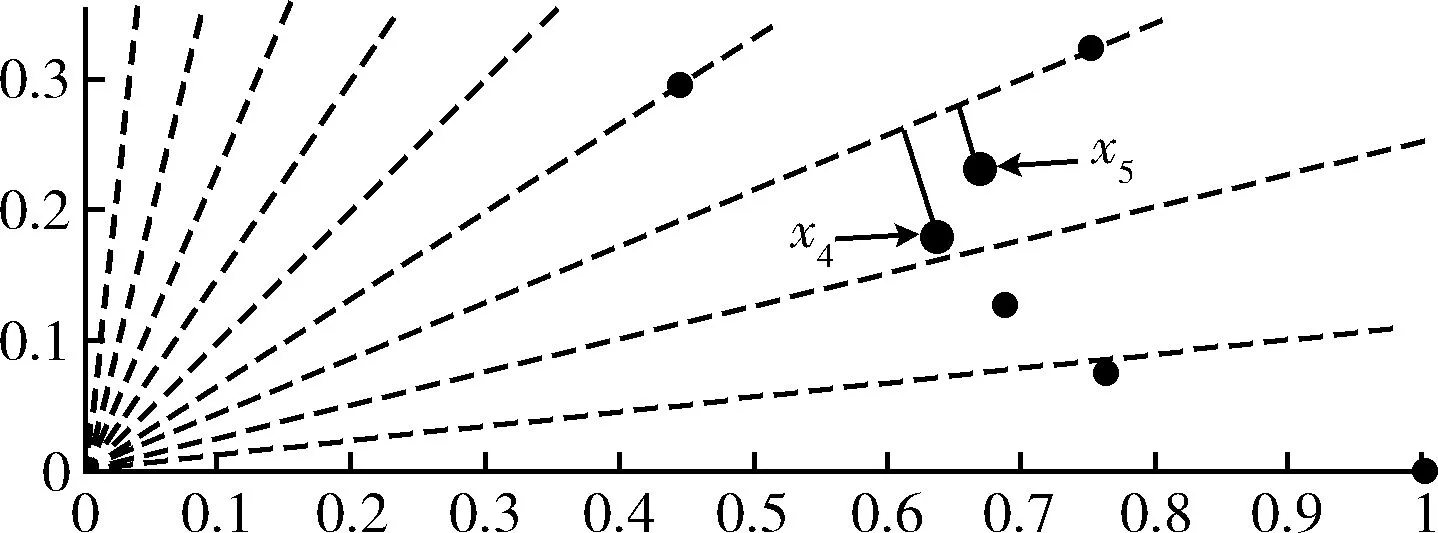
图2 权重向量区域

1.6 算法整体框架

基于上述策略，给出了本文所提出的改进的MOEA/D优化算法框架(I-MOEAD)，具体算法步骤如下：

步骤1 初始化参数、权重向量和初始种群；

步骤2 初始化Pareto外部解集PAS；

步骤3 判断结束条件是否满足，若是，则输出PAS，算法结束；否则，执行步骤4～步骤6。

步骤4 局部搜索策略

(1)遍历当前种群的所有解，执行1.3.1节给出的变异操作算子；

(2)遍历PAS中的所有解，执行1.3.2节给出的强化局部搜索算子；

步骤5 全局搜索策略：循环如下步骤PS/2次：随机选取两个父代个体，执行1.4节给出的交叉算子；

步骤6 种群更新

(1)当前种群全部个体执行快速非支配排序过程，进行Pareto分层；

(2)计算所有个体的PBI值

(3)按照1.5.2节给出的种群更新策略进行候选解的选择，生成下一代种群。同时更新PAS。

(4)跳转到步骤2。

2 实验分析

2.1 实验参数设置

本文所给出的算法主要参数设置如下：权重向量步长σ=0.1，种群大小PS=66，算法终止条件为运行时间100 s。

算法采用VC++编程，在i7 3.4-GHz，16 GB内存PC上独立运行30次，获得的运行结果进行实验分析。

2.2 实验算例生成

某炼钢厂设备配置和加工阶段见表1：①两台连铸机分别可加工两个浇次，该生产期间内共加工4个浇次；②每个浇次分别连续加工5个炉次，该生产期间内共加工20个炉次；③炉次在每个加工阶段其加工时间在[35,50]之间随机选取。

表1 某炼钢厂设备

基于上述实际生产数据，随机生成20个算例验证本文给出的多目标优化算法。

2.3 对比算法

本文选取同样基于MOEA/D的两种算法进行对比分析，即DBEA[24]和EADD[25]。由于上述两种算法是针对连续优化问题，因而本文对其进行重新编码，选取文献给出的参数，以求解多目标HFS调度问题。对比指标采用国际通用的超平面体积(Hypervolume，HV)和反转世代距离(inverted generational distance，IGD)[23-25]。

2.4 实验结果分析

针对随机生成的20个算例，对比结果见表2，表3。由表2可见：①本文给出的I-MOEAD方法在所有的20个随机算例中表现了良好性能，取得了较好解；②平均性能来看，I-MOEAD算法明显优于其它两个对比算法；③HV值的比较结果，验证了本文所提出算法的有效性，也验证了所得结果结合的收敛能力和解的多样性。

由表3可见：①本文给出的I-MOEAD方法在所有的20个随机算例中均取得了较优解；②平均性能来看，I-MOEAD算法明显优于其它两个对比算法；③IGD值的比较结果，进一步验证了本文所提出算法的有效性。

I-MOEAD算法性能优于其它两种比较算法的主要原因分析如下：①全局搜索策略提高了算法求解的多样性和分散性；②两种局部搜索策略，特别是基于关键路径的强化局部搜索策略，进一步提高了算法性能；③种群更新策略，在保持解集质量的前提下，进一步提高了种群的多样性。

3 结束语

为求解多目标HFS调度问题，本文给出了一种改进的MOEA/D优化算法，主要贡献在于：①提出了两种局部搜索策略，即基于交换、插入邻域的局部搜索和基于关键路径的强化局部搜索策略，提高了算法求解的性能。②设计了一种新的交叉算子，提高了算法全局搜索的能力。③设计了一种种群更新策略，进一步提高了算法解集的分布均匀性。

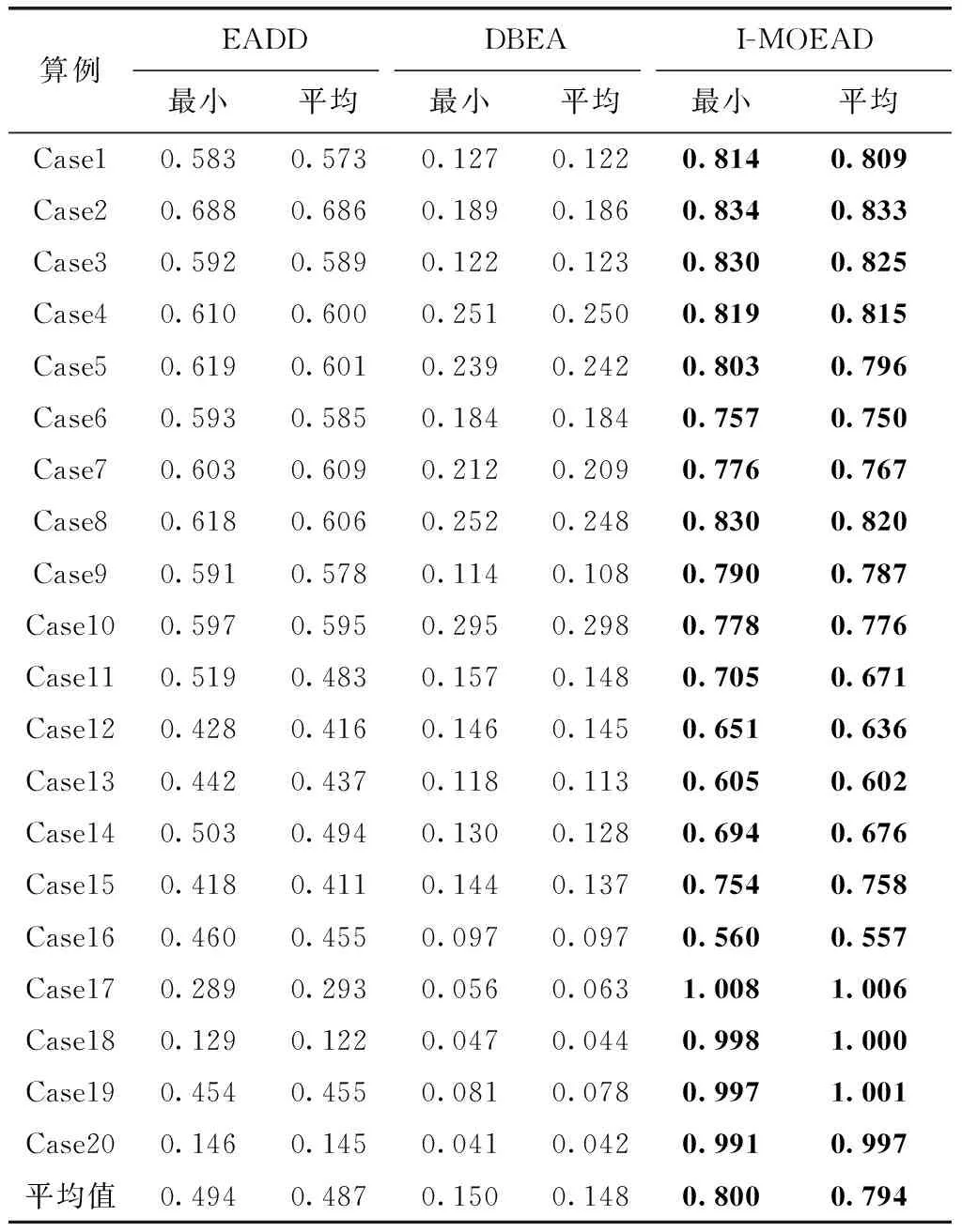
表2 HV值的比较结果

表3 IGD值的比较结果

[1]TIAN Yunna,LI Dongni,ZHENG Dan,et al.A time window-based approach for multi-stage hybrid flow shop[J].Chinese Journal of Mechanical Engineering,2016,52(16):185-196(in Chinese).[田云娜,李冬妮,郑丹,等.一种基于时间窗的多阶段混合流水车间调度方法[J].机械工程学报,2016,52(16):185-196.]

[2]WANG Shengyao,WANG Ling,XU Ye,et al.An estimation of distribution algorithm for solving hybrid flow-shop sche-duling problem[J].ACTA Automatica Sinica,2012,38(3):437-443(in Chinese).[王圣尧,王凌,许烨,等.求解混合流水车间调度问题的分布估计算法[J].自动化学报,2012,38(3):437-443.]

[3]LIU Chang,LI Dong,PENG Hui,et al.EDA algorithm with correlated variables for solving hybrid flow-shop scheduling problem[J].Computer Integrated Manufacturing Systems CIMS,2015,21(4):1032-1039(in Chinese).[刘昶,李冬,彭慧,等.求解混合流水车间调度问题的变量相关EDA算法[J].计算机集成制造系统,2015,21(4):1032-1039.]

[4]Chou F D.Particle swarm optimization with cocktail decoding method for hybrid flow shop scheduling problems with multi-processor tasks[J].International Journal of Production Economics,2013,141(1):137-145.

[5]Pan Q K,Dong Y.An improved migrating birds optimisation for a hybrid flowshop scheduling with total flowtime minimisation[J].Information Sciences,2014,277(2):643-655.

[6]Pan Q K,Wang L,Li J Q,et al.A novel discrete artificial bee colony algorithm for the hybrid flowshop scheduling problem with makespan minimisation[J].Omega,2014,45(2):42-56.

[7]LI Junqing,PAN Quanke,WANG Fatao.Solving hybrid flow-shop scheduling problems by a hybrid discrete artificial bee colony algorithm[J].Operations Research & Management Science,2015,24(1):157-163(in Chinese).[李俊青,潘全科,王法涛.求解混合流水线调度问题的离散人工蜂群算法[J].运筹与管理,2015,24(1):157-163.]

[8]Marichelvam M K,Prabaharan T,Yang X S.Improved cuckoo search algorithm for hybrid flow shop scheduling problems to minimize makespan[J].Applied Soft Computing,2014,19(1):93-101.

[9]LI Zhicong,GU Xingsheng.Improved biogeography-based optimization algorithm used in solving hybrid flow shop scheduling problem[J].CIESC Journal,2016,67(3):751-757(in Chinese).[李知聪,顾幸生.改进的生物地理学优化算法在混合流水车间调度中的应用[J].化工学报,2016,67(3):751-757.

[10]Savsani P,Jhala R L,Savsani V.Effect of hybridizing bio-geography-based optimization (BBO) technique with artificial immune algorithm (AIA) and ant colony optimization (ACO)[J].Applied Soft Computing,2014,21(5):542-553.

[11]Chamnanlor C,Sethanan K,Gen M,et al.Embedding ant system in genetic algorithm for re-entrant hybrid flow shop scheduling problems with time window constraints[J/OL].[2015-04-24].https://link.springer.com/article/10.1007%2Fs10845-015-1078-9.

[12]Pan Q K,Gao L,Li X Y,et al.Effective metaheuristics for scheduling a hybrid flowshop with sequence-dependent setup times[J].Applied Mathematics & Computation,2017,303(6):89-112.

[13]Li J Q,Pan Q K.Solving the large-scale hybrid flow shop scheduling problem with limited buffers by a hybrid artificial bee colony algorithm[J].Information Sciences,2015,316(C):487-502.

[14]Hou Y,Wu N Q,Zhou M C,et al.Pareto-optimization for scheduling of crude oil operations in refinery via genetic algorithm[J].IEEE Transactions on Systems Man & Cyberne-tics Systems,2017,47(3):517-530.

[15]Zhou A,Zhang Q.Are all the subproblems equally important?Resource allocation in decomposition-based multiobjective evolutionary algorithms[J].IEEE Transactions on Evolutionary Computation,2016,20(1):52-64.

[16]Wang J,Zhang W,Zhang J.Cooperative differential evolution with multiple populations for multiobjective optimization[J].IEEE Transactions on Cybernetics,2016,46(12):2848-2861.

[17]Chen Y,Mahalec V,Chen Y,et al.Reconfiguration of satellite orbit for cooperative observation using variable-size multi-objective differential evolution[J].European Journal of Ope-rational Research,2015,242(1):10-20.

[18]ZUO Xingquan,WANG Chunlu,ZHAO Xinchao.Combining multi-objective immune algorithm and linear programming for double row layout problem[J].ACTA Automatica Sinica,2015,41(3):528-540(in Chinese).[左兴权,王春露,赵新超.一种结合多目标免疫算法和线性规划的双行设备布局方法[J].自动化学报,2015,41(3):528-540.]

[19]Wang X,Tang L.A machine-learning based memetic algorithm for the multi-objective permutation flowshop scheduling problem[J].Computers & Operations Research,2017,79(3):60-77.

[20]Long J,Zheng Z,Gao X,et al.A hybrid multi-objective evo-lutionary algorithm based on NSGA-II for practical scheduling with release times in steel plants[J].Journal of the Operational Research Society,2016,67(9):1184-1199.

[21]Lin J,Liu M,Hao J,et al.A multi-objective optimization approach for integrated production planning under interval uncertainties in the steel industry[J].Computers & Operations Research,2016,72(C):189-203.

[22]Gen M,Zhang W,Lin L,et al.Recent advance in hybrid evolutionary algorithms for multiobjective manufacturing scheduling[J/OL].[2017-01-17].http://www.sciencedi-rect.com/science/article/pii/S036083521630523X.

[23]Li K,Deb K,Zhang Q,et al.Efficient nondomination level update method for steady-state evolutionary multiobjective optimization[J/OL].[2016-11-08].http://ieeexplore.ieee.org/document/7738460/.

[24]Asafuddoula M,Ray T,Sarker R.A decomposition-based evolutionary algorithm for many objective optimization[J].IEEE Transactions on Evolutionary Computation,2015,19(3):445-460.

[25]LiK,Deb K,Zhang Q,et al.An evolutionary many-objective optimization algorithm based on dominance and decomposition[J].IEEE Transactions on Evolutionary Computation,2015,19(5):694-716.

[26]Yazdani M,Gohari S,Naderi B.Multi-factory parallel machine problems:Improved mathematical models and artificial bee colony algorithm[J].Computers & Industrial Enginee-ring,2015,81:36-45.