基于自递归峰平扩压的网络信号抑制接收算法

2018-03-19姜宝华吕英华

计算机工程与设计 2018年3期

姜宝华，吕英华

(东北师范大学人文学院计算机系，吉林长春 130117)

0 引言

当前移动通信领域日益朝着融合化、多样化、信号复杂化等方向演进，信号接收过程中频谱、时移特征也呈现混叠化特征[1,2]。然而由于混合通信过程中需要综合考虑的因素较多，如信道抗衰落特性、信号峰值伸展性能等因素，实践中难以针对信号接收方式进行优化，导致混合通信技术适用领域较为狭窄[3]。

为此，学者们提出了诸多解决方案，取得了一定的成果，如Ouyang.A等[4]提出了基于独立正交子载波峰值优化的混合通信信号抑制接收方式，通过将不同频率的信号波拆分为互相独立的OFDM信号，并采取线性功率放大算法，将信号接收强度提升了10-3～10-6数量级，但该算法仅对呈现线性变化规律的OFDM信号具有较好的接收效果，一旦信号在信道传输过程中出现诸如线性受抑制等非独立峰值畸变现象，该算法将出现严重的失真现象；Adali.T等[5]提出了基于拆分映射独立传输序列机制的混合通信信号抑制接收方式，通过将带内频谱进行按抽样点拆分，且将拆分后的频谱进行独立传输的机制，能够在较大幅度内实现对混合通信信号的独立分段抑制接收，但该算法需要采用非线性积分方式实现频谱分段，导致实现过程比较复杂；Nikman.T等[6]提出了基于限幅选择过滤机制的混合通信信号抑制接收方式，利用积分器的选择过滤功能对接收信号的峰值比进行多次滤波，有效对接收信号的扩散频谱进行自适应调整，但该算法需要实现的积分迭代次数较大，增加了系统的实现复杂度，且对物理器件的性能要求很高，降低了该算法的实际部署价值。

为了进一步提高混合通信信号抑制接收方式的信号接收性能，本文依据OFDM模型提出了一种基于自递归峰平扩压机制的混合通信信号抑制接收方式；采用拉格朗日最优法进行信号抑制接收功率系数的裁决，提高了信号接收的峰平比指标性能；依据信号压扩算法，采用分段机制实时构建时域冲激函数，且结合拐点匹配的方式，对带外杂波频率进行屏蔽，提高了本文技术的信号接收性能。仿真实验验证了本文算法的有效性。

1 信号接收模型分析

由于混合通信信号主要采用正交频分复用调制技术(orthogonal frequency division multiplexing，OFDM)进行调制，该方式具有复杂度低、传输带宽高、自信号串扰程度低等特性，特别是OFDM调制具有在广谱杂波干扰下高质量信号传送能力的优势，因此对当前移动通信领域中信号融合趋势具有良好的适应性能[7]。考虑到每路的OFDM信号均由OFDM方式进行独立调制，如图1所示；假设系统当前同时进行的子信号调制的总数为n，Xn为OFDM信号中的第n个子信号，对Xn进行n点IFFT变换处理后可以得到

(1)

图1 OFDM信号调制

由于信号抑制接收过程中需要综合考虑信号功率的接收性能，可以通过考虑信号的最大功率与平均功率的比值情况来进行接收性能评估，因此OFDM信号的抑制接收功率系数PAPR的获取方式如下

(2)

其中，|Xn|为Xn的功率，E[*]表示统计平均；由模型(1)可知，子信号Xn为复数域信号，考虑到OFDM信号的调制特性，当子信号的个数n较大时，Xn的复数域实部信号Re(Xn)和复数域虚部信号Im(Xn)均满足标准正态分布[8]；其功率|Xn|的分布f|Xn|(x)满足标准瑞利分布，可由如下的方式直接获取

(3)

实践中信号接收时均需要按时间进行累加，且需要能够在接收时刻t上获取到信号实时功率F|Xn|(x)，获取方式如下

(4)

不妨设信号在不同的接收时刻t上获取的功率呈现非同分布特性，不妨设信号裁决值为c，则信号抑制接收功率系数PAPR难以达到该裁决值的出现频率可以通过如下方式获取

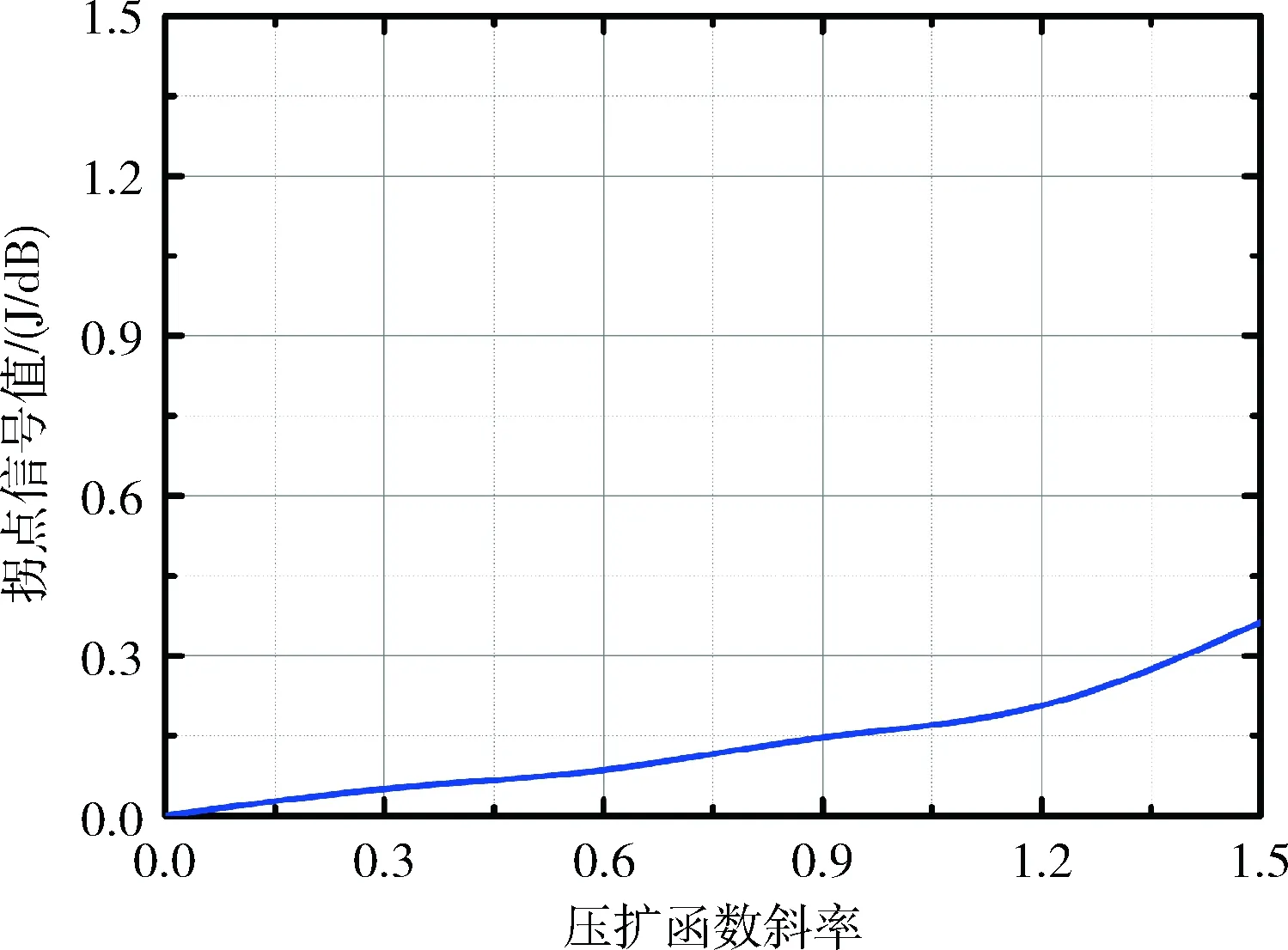
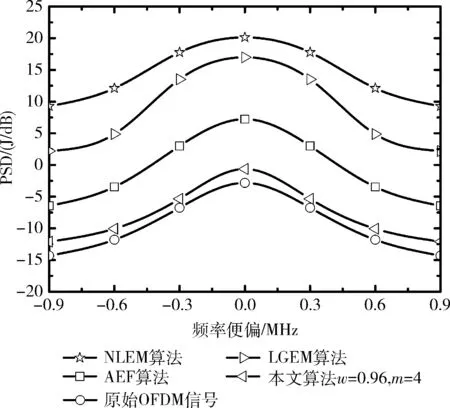
P(PAPR

(5)

显然，信号接收时出现误判情况的概率也可以通过模型(5)获取，数值上与P(PAPR

此外，单纯采取模型(5)的方式虽然能够有效获取信号接收时的误码率数值，然而，模型(5)需要确定接收时刻t，这是由于不同的接收时刻采取模型(5)所获取的误码率也有所不同，而对于混合通信信号接收过程而言，通常采用累积分布的方式计算误码率P(PAPR>c)，由模型(5)可得信号抑制接收功率系数PAPR达到该裁决值的出现频率P(PAPR>c)的获取方式如下

P(PAPR>c)=1-(p{|Xn|2

(6)

在实际过程中，模型(6)能够较好的反映信号抑制接收过程中的误差累积情况，由于该过程可以通过积分器实现，而模型(5)所示的裁决方式一般而言需要通过微分器的方式实现，显然采用模型(6)能够更准确的反映OFDM信号变动趋势，实现起来较为容易。

2 本文混合通信信号抑制接收算法

图2(a)和图2(b)分别显示了本文所提的新接收方式在信号发射前的调制及信号抑制接收过程中的解调过程。在信号发射之前，需要对所获取的时域信号的能量强度进行必要的拓展处理，该拓展处理采用幅度调制的方式，使用非线性函数对信号幅度进行映射处理；随后采用快速傅里叶变换(fast Fourier transform，FFT)的方式进行频域杂波过滤处理，然后采用FFT逆变换(IFFT变换)的方式将信号再次变换为时域信号后，完成本次循环过程。图2(a)中显示了最大迭代次数，当完成M次迭代之后，本次处理过程完毕，信号将以时域的形式被发送；信号抑制接收的过程与信号发射过程互逆，如图2(b)所示，通过FFT变换-IFFT变换及并串变换、解调过程，即可完成整个信号抑制接收过程。

图2 本文接收方式

信号发射前，本文根据拉格朗日最优原理[8]，按模型(5)～模型(6)，构建最佳信号抑制接收功率系数PAPR裁决判定机制，见模型(7)～模型(11)

(7)

(8)

Yn=FFT(Xn)

(9)

(10)

(11)

步骤1 设置初始信号衰减比例系数α，按模型(8)所示获取；将子信号的最大路数设置为迭代最大值M，如图3所示；

步骤2 如图2(a)所示，首先将左端电路进行通断处理，进行第一路子信号的处理；然后将右端电路进行通断处理，使得第一路子信号进入循环状态；

H(m)=1,1≤m≤n-1

(12)

步骤6 对于完成滤波过程的信号进行逆向傅里叶变化处理，得到最终的待传输信号；此时，将电路的右端进行通断处理，输出信号；再将电路的左端进行通断处理，并转步骤1进行下一个子信号的处理。

图3 子信号过滤处理流程

从图2(a)得知，本文信号抑制接收方式中，对信号的压扩处理要求较高，因此采用传统按段处理方式[9]将难以做到对模型(12)所示的时域冲击响应函数进行实时匹配，因此本文信号抑制接收方式中采用拐点思想；函数扩压采用非对称线性函数方式，以信号波动强度与拐点值进行匹配，将信号进行分段处理，压扩函数Hn如下所示

(13)

其中，m为线性函数的斜率，拐点μ最大设置为原始信号的最大值max|Xn|；在进行信号拓展过程中，为保持信号功率不受影响，信号功率应该满足如下判别式

E{|Xn|2}=E{|Yn|2}

(14)

代入模型(3)～模型(4)可得

(15)

化简模型(15)可得

(16)

按模型(16)对m和μ进行数值建模，可以得到两者的变化曲线如图4所示。可见，两者呈现较好的正比例相关关系，故可近似写为

μ=0.724m

(17)

图4 数值模拟关系

(18)

其中，Yn为接收到的信号，至此完成了整个信号的调制及解调过程，信号抑制接收过程完毕，能够进行信号的正常解调。

3 本文方法性能分析

3.1 峰平比性能分析

OPDM信号在进行图2(a)所示的压扩之后，其PAPR为

(19)

3.2 信号误码率分析

由于本文方法主要采用了模型(13)及模型(18)所示的方式进行信号压扩，进行完压扩处理后的信号Yn可以看作是原始信号Xn衰减的基础上，引入了一个杂波噪声Cn

Yn=ωXn+Cn

(21)

其中，ω为衰减系数，由于OFDM信号具有时域信号不变的特性[11]，因此根据模型(3)及模型(13)并结合该特性，可以获得衰减系数ω的计算公式如下

(22)

联合模型(3)、模型(11)并结合模型(22)可得ω的数值表达式为

(23)

图5显示了按模型(23)所示得到的衰减系数ω与斜率倒数m之间的数值关系；由图可知，衰减系数ω与斜率倒数m之间呈现明显的正相关线性关系；当衰减系数ω较大时，接收到的信号强度也较大，系统误码率(system error rate，SER)性能也就越好，即本文信号抑制接收方式可以通过动态调整模型(13)所示的压扩函数Hn，从而实现SER性能的最优；此外，由于本文的压扩函数Hn均严格呈现线性关系，实践中仅仅需要进行斜率调制即可，且线性函数仅需要简单低通方法即可实现，有效提高了本文方案的实践价值。

图5 ω与m数值关系

综上所述，由于OFDM信号调制中峰平比性能与SER性能呈现负相关关系，即对于任意一种OFDM信号调制而言，不能够同时达到峰平比性能与SER性能最佳。从模型(17)～模型(20)可知，随着压扩函数斜率的不断增加，采取线性压扩方式能够实现较好的PAPR性能增益，但是该增益仅限于时域部分，且采用压扩方式将直接降低衰减系数ω，致使信号的SER性能呈现剧烈降低的态势。采用本文方法可以根据具体的OFDM参数情况，动态调整性能，如图3、图4所示；此外由于本文方案对于压扩带来的频率扩展问题能够实现实时消除，信号的带宽外的杂波频率可以进行直接抑制，可以避免不同子信号之间产生的信号频率串扰现象。

4 仿真实验

为验证本文方案的有效性，采用NS2仿真环境进行仿真实验，对照组实验采取当前常见的幅度能量滤波限制方式[12](amplitude energy flter，AEF)、自然对数扩展方式[13](natural logarithmic expansion method，NLEM)、线性增益扩展方式[14](linear gain expansion mode，LGEM)。系统仿真参数采用不编码的OFDM系统，子信号总数N=2048，信号接收星座采用256QPSK星座图及512QFSK星座图；单路子信号的符号总个数不超过1024个。

图6显示了初始状态下OFDM信号的SGC曲线，以及采用不同抑制方式获取得到的OFDM信号增益曲线(signal gain curve，SGC)状况。由图6可知，本文方案衰减系数ω=0.96且压扩函数斜率倒数m=4时所获取的SGC曲线性能最优，与初始状态下OFDM信号的SGC曲线状况最为接近，而对照组方式均与OFDM信号的SGC曲线的波形有较大状态的出入；此外,本文技术在衰减系数ω=0.96且压扩函数斜率倒数m=4时所获取的PAPR性能与初始OFDM信号的OFDM信号性能仅相差不足2 dB，均要远远好于对照组方法。此外，由于本文方案能够动态的调制衰减系数及压扩函数斜率，能够适应OFDM信号的时不变特性，可以通过调整衰减系数及压扩函数斜率的方式，不断逼近原始信号的SGC曲线，具有良好的实际使用价值。AEF方式由于单纯采取能量幅度限制压扩方式，当能量幅度波动剧烈时将导致带外杂波频繁的产生，因而降低了OFDM信号的接收性能；NLEM方式的冲激函数基于自然对数映射方式产生，虽然与OFDM信号的波形匹配程度较好，然而由于OFDM信号波形在频域上具有时变特性，导致冲激函数的滚降性能较差，在调制阶数较高时将有效削弱信号增益，导致SGC曲线出现抖动；LGEM方式由于采用线性映射及压扩方式，导致滚降系数为标准低通曲线，当系统进行高阶调制时其带外频率呈现广谱特性，难以通过低通及带通方式进行过滤，导致信号接收性能不如本文方案。

图6 不同算法的SGC曲线性能测试

图7、图8分别显示了采用本文方法与对照组方法在256QPSK星座图及512QFSK星座图接收策略下，通过标准莱斯信道后获取得到的OFDM系统误码率(system error rate，SER)性能曲线。由图可知，在衰减系数ω=0.96，且压扩函数斜率倒数m=4时，本文机制获取的SER性能曲线最好。由图7可知，本文方案的SER性能远远高于AEF方式、NLEM方式及LGEM方式，这是由于本文在OFDM调制基础上，采用迭代方式针对每路子信号的特性进行循环滤波处理，且采用拉格朗日方法实现了信号抑制接收功率系数的最优匹配，因而SER性能较好；AEF方式及NLEM方式均采用一次成型机制，单路子信号在进行初始滤波之后即被发送到传输信道中，其信号抑制接收功率系数无法通过循环滤波方式进行优化匹配；LGEM方式虽然也采取循环滤波方式，能够对信号抑制接收功率系数进行优化匹配，然而由于该方式的滚降系数为定值，无法对发射波形进行匹配发射，导致接收时信号波形发生较大幅度的畸变现象，从而降低了SER性能。

图7 4种算法的SER曲线性能测试(256QPSK星座图)

图8 4种算法的SER曲线性能测试(512QFSK星座图)

从图8可知，本文方法在512QFSK星座图接收策略下的SER性能亦具有相当程度的优势，与初始状态下OFDM信号的SER曲线的拟合程度较高，且在SER性能在10-8层次上的优势更为明显，具有良好的拟合特性。AEF方式和NLEM方式的信号在进行一次调制完后即被发射，导致信号抑制接收功率出现较大幅度的衰减，其SER曲线性能显然要低于本文方式所采用的循环滤波方式；而LGEM方式虽然采用类似的方式对信号抑制接收功率系数进行优化匹配，然而由于未能采取本文算法所使用的动态滚降系数生成方式，导致信号波形鲁棒性较差，接收时较本文方案而言更容易产生波形畸变现象，因而其SER性能要低于本文方案。

根据上述实验可知，在ω=0.96且压扩函数斜率m=4时所获取的PAPR性能与初始OFDM信号的OFDM信号性能非常接近，为了节省成本，本文择取ω=0.96、m=4条件下的本文算法与LGEM、AEF以及NLEM进行了对比测试功率谱密度。图9显示了本文方法与对照组方法接收信号的功率谱密度曲线(power spectral density，PSD)，由图可知，由于本文方法能够通过迭代方式将信号带宽外所产生的杂波频率进行过滤，基本消除了因采用压扩方式而导致的杂波频率衍生的问题，与初始状态下OFDM信号的PSD性能相比极为接近；特别是在OFDM信号中心频率附近时，本文方法的PSD增益已达到10 dB以下，能够有效避免临近子信号的互相串扰现象；且发射波形与初始状态下OFDM信号波形最为接近，具有显著的优势。AEF方式及NLEM方式均采用一次成型滤波的方式对信号能量幅度进行成型处理，由于该成型方式均采用线性成型方式，且其频率域中成型曲线为高斯曲线，导致发射时其成型曲线与OFDM信号发生卷积平移时出现严重的频率混叠现象，且由于杂波频率混叠而导致PSD曲线出现抖动现象；LGEM方式由于其滚降系数为定值，且其压扩方式采取线性压扩方式，导致成型时难以通过滤波方式对杂波频率进行过滤处理，增加了功率谱密度抖动现象发生的概率，从而使得其PSD曲线出现波动现象。

图9 各算法的PSD曲线性能测试

综上所述，本文方案能够在莱斯干扰条件下能够取得比AEF方式更好的峰平比性能；且SER性能要远远优于NLEM方式及LGEM方式；且PSD发射波形也与OFDM信号波形最为接近，能够有效的对杂波频率干扰产生抑制；特别是在超高阶调制星座(256QPSK星座图、512QFSK星座图)下依然能够获取良好的SER曲线性能，说明本文方案能够有效提高系统的误码率性能。

5 结束语

为解决当前混合通信系统中信号抑制接收技术存在多径衰落严重、抗噪性能降低、频率混叠化严重等不足，本文提出了基于自递归峰平扩压机制的混合通信信号抑制接收方式。该方式首先通过拉格朗日最优法实现信号抑制接收功率系数的裁决，增强了信号峰平性能，改善了信号发射时难以提高PAPR性能的不足；其次采用非线性函数压扩方式，结合拐点匹配思想，采用分段方式实现对带外杂波频率的实时迭代屏蔽，进一步提高了本文方案的信号接收性能。

下一步，将针对本文方案需要基于OFDM算法的不足，通过引入拉普拉斯频率逆变换机制，将互相独立的子信号压扩为单路发射的一次波形，进一步改善本文方案在复杂通信领域中的适用性能。

[1]CHEN Ming,XIAO Jiangnan.The study of real time optical OFDM transmitter based on FPGA[J].Journal of Optoelectronics Laser,2013,24(1):63-68(in Chinese).[陈明,肖江南.基于FPGA的实时光OFDM发射机的研究[J].激光技术,2013,24(1):63-68.]

[2]HUANG Min,LI Bingbing.Joint channel estimation and OFDM signal detection algorithm based on total least squares[J].Journal of Electronics and Information,2014,36(6):1448-1453(in Chinese).[黄敏,李兵兵.基于整体最小二乘的联合信道估计及OFDM信号检测算法[J].电子与信息学报,2014,36(6):1448-1453.]

[3]MA Yongqiang.OFDM ultra wide channel estimation based on compressed sensing and particle filter[J].Computer Measurement and Control,2015,23(6):113-129(in Chinese).[马永强.基于压缩感知和粒子滤波的OFDM超宽信道估计[J].计算机测量与控制,2015,23(6):113-129.]

[4]Ouyang A,Tang Z,Zhou X,et al.Parallel hybrid PSO with CUDA for ID heat conduction equation[J].Computer & Fluids,2015,110(1):198-210.

[5]Deng ML.Fiber nonlinearity compensation for CO-OFDM transmission with 10.7-Gb/s NRZ-OOK neighbors[J].Chinese Optics Letters,2013,11(2):127-144.

[6]Nikman T.New self-adaptive inspired algorithm for unit commitment problem[J].IET Science Measurement & Technology,2014,8(6):505-517.

[7]Navaratnarajah S,Saeed A,Dianati M,et al.Energy efficiency in heterogeneous wireless access networks[J].IEEE Wire Communications,2013,20(2):37-43.

[8]Xu Q,Quan X,Pan WS.Frequency diversity for OFDM mobile communication via underwater acoustic channels[J].Journal of Marine Science and Application,2013,1(2):37-43.

[9]Jaddi NS.Optimization of neural network model using modified bat inspired algorithm[J].Applied Soft Computing,2015,37(17):71-86.

[10]Yang ZY.A convex geometry-based blind source separation method for sepatating nonnegative sources[J].IEEE Transitions on Neural Networks and Learning Systems,2015,26(8):1635-1644.

[11]Li XW,Luo J.LTE system DCI format detection and implementation of PDSCH transmission scheme[J].TV Technology,2013,17(12):204-208.

[12]Xu XK,Chen J.Parameterizing both path amplitude and delay variations of underwater acoustic channels for block decoding of orthogonal frequency division multiplexing[J].IEEE Trans Broadcasting,2014,46(11):1177-1192.

[13]Rahmatallan Y,Mohan S.Peak-to-average power ratio reduction in OFDM systems:A survey taxonomy[J].IEEE Communications Surveys & Turorials,2013,15(4):1567-1592.

[14]Jiang T,Li C.Simple alternative multisequences for PARA reduction without side information in SFBC MIMO-OFDM systems[J].IEEE Trans Vehicular Technology,2012,61(7):3311-3315.