两类Lorenz型混沌模型的动力学行为研究*

张付臣， 陈 睿， 陈修素，李如意， 曾 偲， 何毅章

(1. 重庆工商大学 数学与统计学院， 重庆 400067；2.重庆工商大学 信息化办公室， 重庆 400067；3. 成都市第七中学， 成都 610041)

1 研究背景

1963年，美国气象学家Lorenz[1]在研究大气运动时发现了第一个具有“蝴蝶效应”的Lorenz混沌系统，大量专著和论文研究了Lorenz混沌系统的定性与定量动力学行为，包括奇点及其稳定性、奇点的局部拓扑结构和平衡点的局部分岔、同宿轨线和异宿轨线的扰动与保持性、周期解的存在性及其稳定性、混沌同步与控制等[2-12]。Lorenz混沌系统、Chua’s电路系统、Rössler系统、Chen系统、Lu系统等混沌系统在自然科学和工程领域都有着广泛的应用[13-15]。

2 主要数学结果

一类用于描述Couette-taylor流复杂动力学行为的三维Lorenz型混沌系统[16]

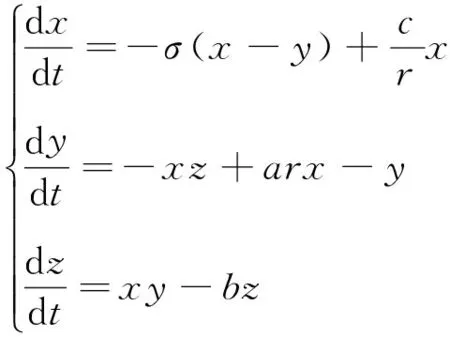
(1)

其中a，b，c，r，σ为混沌系统(1)的正参数。且有r为系统式(1)的雷诺参数，σr-c>0。

一类用于描述不可压缩磁流体动力学行为的方程为[17]

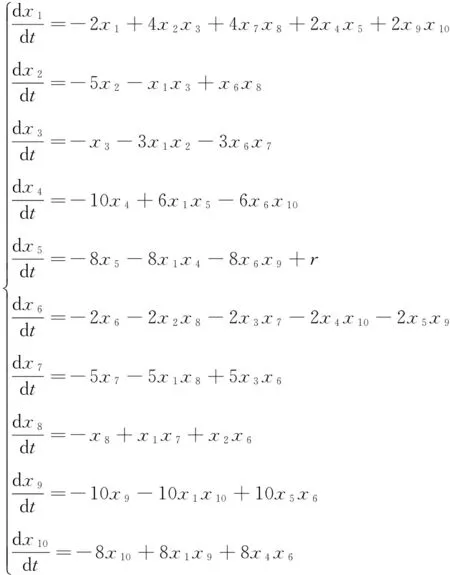
(2)

其中r>0为混沌系统式(2)的雷诺参数，决定着系统式(2)的分岔和混沌行为。

混沌系统式(1)和式(2)奇点的局部分岔、李雅普诺夫指数、庞加莱截面、功率谱及其返回映射等在文献[16-17]中已经研究过。下面将研究系统式(1)和式(2)的最终界和全局吸引域。

定理1 对任意的a>0，b>0，r>0，σ>0，σr>c>0，则

R2，∀m>0，∀λ≠0}

(3)

是系统式(1)的一个最终界与正向不变集。这里

证明定义广义李雅普诺夫函数

(4)

沿着系统式(1)正半轨线求导数

-2dmx2-2λ2y2-2bλ2z2+2b(σm+arλ2)z，

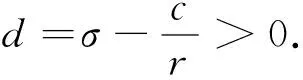
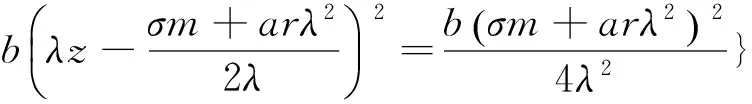
(5)

上述问题等价于：

引入新的变量，令

则上述问题转化为

通过计算可以得到：

容易证明式(3) 为混沌系统式(1)正半轨线的一个最终有界集和正向不变集。

定理2 令X(t)=(x(t)，y(t)，z(t))为系统式(1)的任意一个解。则对于任意a>0，b>0，r>0，σ>0，σr>c>0， 令

V(X)=V(x，y，z)=mx2+λ2y2+

θ=min(b，d，1)>0，d=

则当V(X(t))>Lλ，m，V(X(t0))>Lλ，m时，对于系统式(1)的轨线有如下估计式

V(X(t))-Lλ，m≤〈V(X(t0))-Lλ，m〉e-θ(t-t0)

从而

Ψ={(x，y，z)|mx2+λ2y2+

(6)

为系统式(1)的一个全局指数吸引集。

证明定义广义李雅普诺夫函数

V(X)=V(x，y，z)=mx2+λ2y2+

对上述广义李雅普诺夫函数求导数

-2dmx2-2λ2y2-2bλ2z2+2b(σm+arλ2)z≤

-dmx2-λ2y2-bλ2z2+2b(σm+arλ2)z=

当V(X(t))>Lλ，m，V(X(t0))>Lλ，m，则有

V(X(t))≤V(X0)e-θ(t-t0)+Lλ，m(1-e-θ(t-t0))

整理得

V(X(t))-Lλ，m≤〈V(X0)-Lλ，m〉e-θ(t-t0)

让t→+∞， 且对上面不等式两边取上极限有

从而有

Ψ={(x，y，z)|mx2+λ2y2+

为系统式(1)的一个全局指数吸引集。

定理3 令X(t)=(x1(t)，x2(t)，x3(t)，x4(t)，x5(t)，x6(t)，x7(t)，x8(t)，x9(t)，x10(t))为系统式(2)的任意一个解。则对于任意r>0， 令

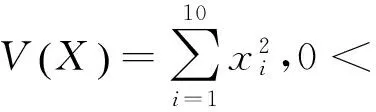
则当V(X(t))>M，V(X(t0))>M时，对于系统式(2)的正半轨线有如下的估计式

V(X(t))-M≤〈V(X(t0))-M〉e-θ(t-t0).

从而

(7)

为系统式(2)的一个全局指数吸引集。

当V(X(t))>M，V(X(t0))>M，则有

V(X(t))≤V(X0)e-θ(t-t0)+M(1-e-θ(t-t0))

整理得

V(X(t))-M≤[V(X0)-M]e-θ(t-t0)

让t→+∞， 且对上面不等式两边取上极限有

从而Ψ1={(x1，x2，x3，x4，x5，x6，x7，x8，x9，x10)|

3 结 论

研究了两类混沌模型的全局吸引性和最终界，研究方法适用于其他混沌系统的研究，研究结果对混沌系统的混沌控制的应用将起到一定的参考价值。

[1] LORENZ E N. Deterministic Non-periods Flows[J]. Journal of the Atmospheric Sciences， 1963， 20:130-141

[2] BALLESTEROS A， BLASCO A， MUSSO F. Integrable Deformations of Rössler and Lorenz Systems from Poisson-Lie Groups[J]. Journal of Differential Equations， 2016， 260(11): 8207-8228

[3] COOMES B A. The Lorenz System does not Have a Poly-nomial Flow[J]. Journal of Differential Equations， 1989， 82(2): 386-407

[4] LEONOV G A. On Estimates of the Bifurcation Values of the Parameters of a Lorenz System[J]. Russian Mathematical Surveys， 1988， 43(3): 216-217

[5] WU K S， ZHANG X. Darboux Polynomials and Rational First Integrals of the Generalized Lorenz Systems[J]. Bulletin Des Sciences Mathématiques， 2012， 136(3): 291-308

[6] DOEDEL E J， KRAUSKOPF B， OSINGA H M. Global Organization of Phase Space in the Transition to Chaos in the Lorenz System[J]. Nonlinearity， 2015， 28(11): 113-139

[7] YANG Q G， ZHANG K M， Chen G R. Hyperchaotic Attractors from a Linearly Controlled Lorenz System[J]. Nonlinear Analysis: Real World Applications， 2009， 10(3): 1601-1617

[8] ZHANG F C， ZHANG G Y. Further Results on Ultimate Bound on the Trajectories of the Lorenz System[J]. Qualitative Theory of Dynamical Systems， 2016， 15(1): 221-235

[9] ZHANG F C， MU C L， ZHOU S M，et al. New Results of the Ultimate Bound on the Trajectories of the Family of the Lorenz systems[J]. Discrete and Continuous Dynamical Systems-series B， 2015， 20(4): 1261-1276

[10] ZHANG F C， LIAO X F， MU C L. On Global Boundedness of the Chen System[J]. Discrete and Continuous Dynamical Systems-Series B， 2017， 22(4): 1673-1681

[11] ZHANG F C， LIAO X F， ZHANG G Y，et al. Dynamical Analysis of the Generalized Lorenz Systems[J]. Journal of Dynamical and Control Systems， 2017， 23(2): 349-362

[12] ZHANG F C， LIAO X F， ZHANG G Y，et al. Dynamical Behaviors of a Generalized Lorenz Family[J]. Discrete and Continuous Dynamical Systems-Series B， 2017， 22(10): 3707-3720

[13] SPARROW C. The Lorenz Equations:Bifurcations Chaos and Strange Attractors[M].New York：Springer Science & Business Media， 2012

[14] BRAGIN V， VAGAITSEV V.Algorithms for Finding Hidden Oscillations in Nonlinear Systems[J]. Journal of Computer and Systems Sciences International， 2011， 50: 511-543

[15] LIU X W， CHEN T P. Boundedness and Synchronization of Y-coupled Lorenz Systems with or Without Controllers[J]. Physica D: Nonlinear Phenomena， 2008， 237(5): 630-639

[16] WANG H Y. The Dynamical Behavior and Numerical Simulation of Lorenz Equations of Spiral-flow Type Systems[J]. Numerical Mathematics A Journal of Chinese Universities， 2016， 38(3): 201-212

[17] WANG H Y. The Dynamical Behaviors and Numerical Simulation of a Five-mode Lorenz-like System of the MHD Equations for a Two-dimensional Incompressible Fluid on Attorus[J]. Acta Mathematica Scientia， 2017， 37(1): 199-216