基于射影几何的极点和极线理论应用与研究*
2018-03-19陈方玉曾昌涛
陈方玉, 曾昌涛
(重庆市第八中学校, 重庆 400030)
在此从1道重庆市2016年“一诊”考题说起,题目如下:
引例(重庆2016年“一诊”16题)如图1所示,过直线x+y=2上任意一点P向圆C:x2+y2=1作两条切线,切点分别为A,B,线段AB的中点为Q,则点Q到直线l的距离的取值范围为 .

图1 引例圆C坐标图
首先给出解析法:
解答设点P(t,2-t),则经过O,A,P,B4点的圆的方程为
即x2-tx+y2-(2-t)y=0
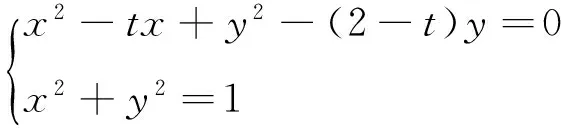
得两圆的相交弦AB方程为tx+(2-t)y=1(也可直接由切点弦方程的公式直接给出),而直线OP方程:(2-t)x-ty=0
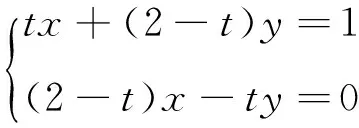
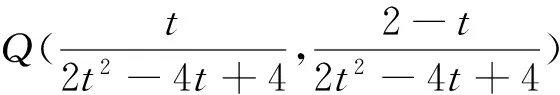
则点Q到直线l的距离为
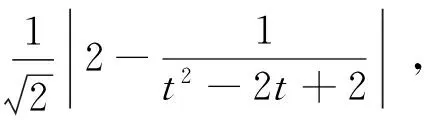
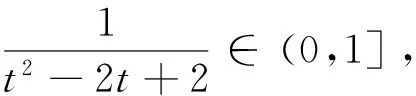
此题解析法关注点Q坐标的表示以及距离d的取值范围的求解,思路清晰,但计算比较繁琐,其实可以探求此题的射影几何背景.其本质上是一种繁衍变换,为了从这个角度来思考问题,下面先介绍一些相关的概念和性质.
1 调和点列

性质1 共轭性
若点A,B被点C,D调和分割,同时点C,D也被点A,B调和分割.
性质2 调和性
性质3 等比性
若AB中点为M,则有MB2=MC·MD.
2 极点、极线
2.1 定 义

特别地,点P对有心二次曲线(设其中心为O)的调和共轭点为Q,且PQ通过中心O,则称点P变到点Q的变换称为反演变换,O为反演中心,P,Q互为反点.显然由调和点列的等比性,若P,Q互为反点,有OP·OQ=OR2成立.
结合完全四边形的性质,还可以得到一个有趣的结论:如图2所示,A,B是圆锥曲线C的一条对称轴l上的两点(不在C上),若A,B关于C调和共轭,过B任作C的一条割线,交C于P,Q两点,则∠PAB=∠QAB.

图2 圆锥曲线C
(2) 不在二次曲线Γ上的定点P关于二次曲线的调和共轭点轨迹是一条直线,这条直线l叫做P关于此二次曲线的极线,P为这条直线l关于此二次曲线的极点.
二次曲线Γ上的点P关于Γ的极线为二次曲线在P处的切线.
2.2 圆锥曲线中极线的方程
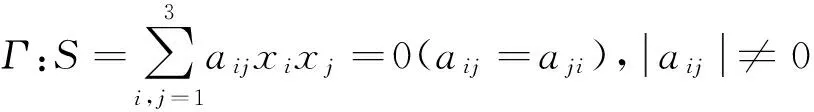
所以点P(x0,y0)关于二次曲线Γ:Ax2+Bxy+Cy2+Dx+Ey+F=0的极线方程为
即(2Ax0+By0+D)x+(Bx0+2Cy0+E)y+Dx0+Ey0+2F=0.
特别地:
(3) 对于抛物线y2=2px,与点P(x0,y0)对应的极线方程为y0y=p(x0+x).
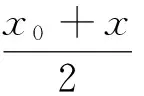
2.3 配极原则
如果点P的极线通过点Q,则点Q的极线也通过点P
配极原则是一种特殊的对偶原则,规定了一个点列与其对应线束之间的一个射影对应.由配极原则,不难得到共线点的极线必共点,共点线的极点必共线.
由此,可以解决文章开头提出的问题,解析如下:
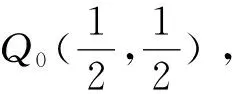
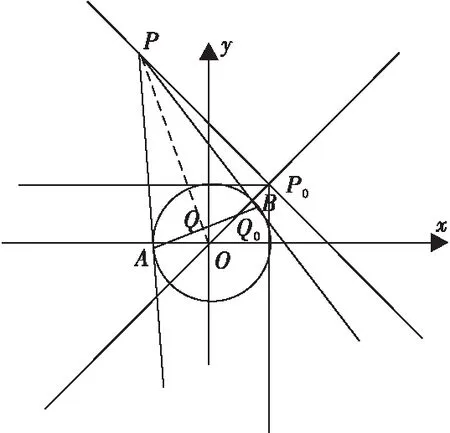
图3 引例解析坐标图C
2.4 极线的作图方法
若一个三角形每一个顶点关于二次曲线的极线都是其对边(每边的极点也是其所对顶点),则称三角形为自极三角形.内接于二次曲线Γ的完全四点形ABCD的对边三点形△PQR为自极三角形(如图4).
由此,可以得到定点P关于二次曲线Γ的极线的作法:
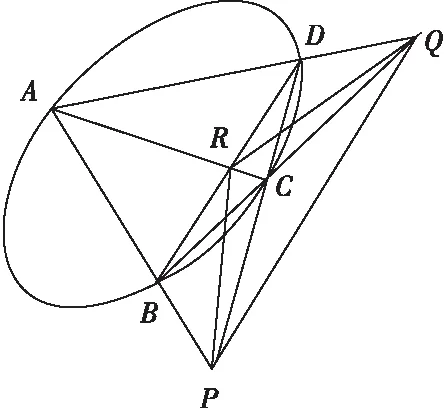
图4 自极三角形
如图5(a),P为不在二次曲线Γ上的点,过点P引两条割线依次交二次曲线于4点E,F,G,H,连接EH,FG交于N,连接EG,FH交于M,则MN为点P对应的极线.
在图5中,还得到了过二次曲线Γ外一点P切线的作法:如图5(b),事实上,连接MN交二次曲线Γ于A,B两点,则PA,PB恰为二次曲线的两条切线.
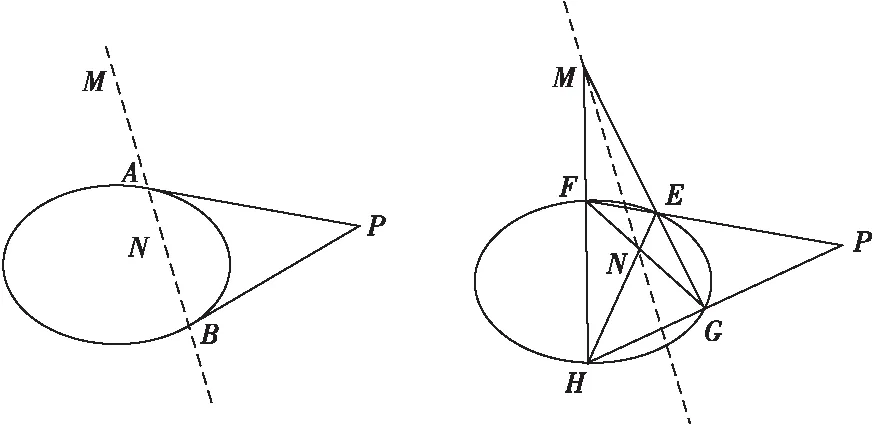
(a) (b)
3 极点、极线理论的应用
极点、极线理论虽然在高中课标内没有要求,但作为圆锥曲线的一种基本特征,无论是在教材中还是在各地的高考试题和模拟试题中以此为背景的题目屡见不鲜,一线教师了解一些极点、极线理论,可以以较高的观点去看待试题,有利于中学数学教学中的优生指导和试题研究.
3.1 极点、极线的直接应用:判断直线与圆锥曲线的位置关系
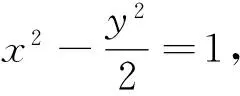
解析设A(x0,y0),则由P是线段AB的中点得B(2-x0,2-y0),而A,B在双曲线上,故

变式(人教A选修2-1 2.4.2例6)已知抛物线的方程为y2=4x,直线l过定点P(-2,1),斜率为k.k为何值时,直线l与抛物线y2=4x:只有一个公共点;有两个公共点;没有公共点?
例2 (2016年全国新课标卷(文科)20题)如图6,在直角坐标系xOy中,直线l:y=t(t≠0)交y轴于点M,交抛物线C:y2=2px(p>0)于点P,点M关于点P的对称点为N,连接ON并延长交C于点H.
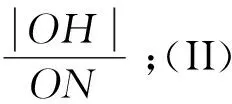
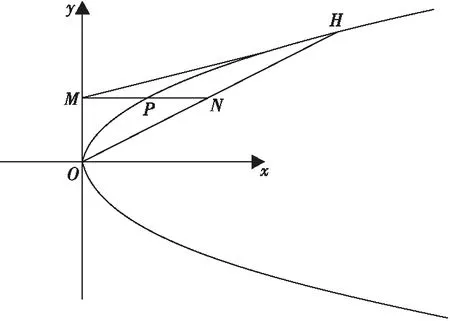
图6 例2抛物线C坐标图

3.2 极点、极线性质的深层体现
例3 (2015年全国1卷理科20题)
曲线C:x2=4y与直线y=kx+a(a>0)交于M,N两点.
(I) 当k=0时,分别求C在点M,N处的切线方程;
(II)y轴上是否存在点P,使得当k变动时,总有∠OPM=∠OPN,说明理由.
解析(I)略;在(II)中,直线y=kx+a与y轴的交点为Q(0,a),它关于抛物线的共轭点是其关于顶点的对称点P(0,-a),则根据调和共轭的性质知:P(0,-a)满足∠OPM=∠OPN.
类似的,2015年福建文科第19题、2015年四川理科第20题都是利用本题中调和共轭点的这一性质进行命制的.
例4 (2010年江苏文、理科18题)
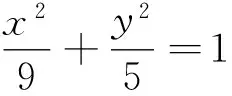
(I) 设动点P满足PF2-PB2=4,求点P的轨迹;
(III) 设t=9,求证:直线MN必过x轴上的一定点(其坐标与m无关).
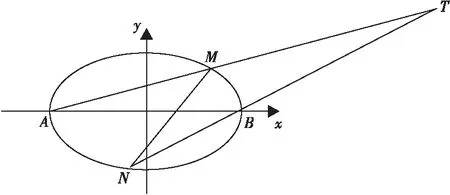
图7 例4椭圆坐标图

例5 (2011年四川理科21题)
如图8,椭圆两顶点A(-1,0),B(1,0),过其焦点F(0,1)的直线l与椭圆交于C,D两点,并与x轴交于点P.直线AC与直线BD交于点Q.

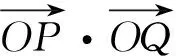

图8 例5椭圆坐标图

类似地,2008年安徽理科第22题、2011年山东文科第22题、2011年四川文科第21题、2012年北京理科第19题也是利用极点、极线的寻找或者性质为背景命制,另外,还可以看到极点、极线的理论在面对解析几何中定值、定点问题的处理时,往往会带来意想不到的解题思路或者突破口.
例6 (1995年全国卷理科26题)

图9 例6椭圆C坐标图
解析由题,点P,Q互为反点,点Q是点P的极线与射线OP的交点.

此题其实是对反演变换的一种推广,广义反演变换把通过反演中心的直线仍然变为直线本身,把不通过反演中心的直线变成通过反演中心,对称轴与基椭圆的对称轴平行且与基椭圆相似的椭圆.
类似地, 2015年北京理科第19题也是以反演变换和反演点性质为背景命制.
例7 过抛物线y2=2px的焦点的一条直线和此抛物线相交,两个交点纵坐标为y1,y2,求证:y1y2=-p2.
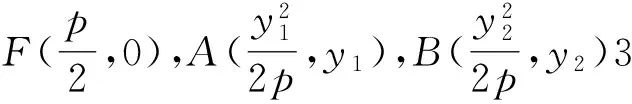
变式(2006年全国2卷理科21题)
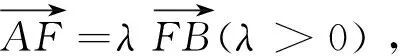

(II) 设△ABP的面积为S,写出S=f(λ)的表达式,并求S的最小值.
相比例1—例4中以极点、极线为背景命制试题,例5及变式是对极点、极线中配极原则的应用. 如果用类似的处理方法解决2005年江西理科第22题,会使运算过程大幅度简化,也会给认识问题本质提供方向.
当然以上解析直接作为解题的解答过程显然是不合适的,但上述分析过程可以帮助教师和高水平的学生理解试题的背景或者探求解题的方向. 我们一直相信:一个有科学精神的人,在研究一个问题的时候,第一件事就是遥望一下这个问题的结果!问题研究的过程,从来都是“大胆猜想,小心论证”的过程.
4 结束语
极点、极线理论在高等几何中对二次曲线描述是极为重要的一个基本特征. 教师可以通过对二次曲线在射影几何的观点下多加研究,引导学生用射影几何的方法处理中学解析几何问题. 这样既能帮助学生利用旧知识去理解新知识,反过来又能用新知识解决旧问题,使新旧知识结合起来,这无疑对于指导学生从更高层次理解中学数学内容,从而更深层次地把握几何知识的内在联系和本质有积极的意义.
[1] 周兴和,杨明升. 高等几何(第三版)[M]. 北京:科学出版社,2015
ZHOU X H,YANG M S. Advanced Geometry (Third Edition)[M]. Beijing: Science Press, 2015
[2] 沈文选,杨清桃. 高中数学竞赛解题策略 几何分册[M]. 杭州:浙江大学出版社,2012
SHEN W X, YANG Q T. Geometric Section of Problem Solving Strategy in Senior High School Mathematics Competition[M]. Hangzhou: Zhejiang University Press, 2012
[3] 李三平. 高观点下的中学数学[M].西安:陕西师范大学出版社,2013
LI S P. High School Mathematics under High Viewpoint[M]. Xi’an:Shaanxi Normal University Press, 2013
[4] 苏步青.高等几何讲义[M].上海:上海科学技术出版社,1964
SU B Q. Lectures on Advanced Geometry[M]. Shanghai: Shanghai Science and Technology Press, 1964
[5] 单墫. 解析几何的解题技巧[M].合肥:中国科学技术大学出版社,2009
SHAN Z. Solving Skills of Analytic Geometry[M]. Hefei: University of Science & Technology China Press, 2009
[6] 樊真美. 95年高考试题轨迹题的引申——广义反演变换[J]. 南京高师学报,1996(12):1-6
FAN Z M. The Extension of 95 Year College Entrance Examination Questions Generalized Inverse Transform [J]. Journal of Nanjing Normal University, 1996 (12) :1-6
[7] 李凤华. 圆锥曲线的极点与极线及其应用[J]. 数学通讯,2012(4):41-45
LI F H. Poles and Poles of Conic Curves and Their Applications [J].Mathematical Communication, 2012 (4): 41-45
[8] 曾昌涛,谭卫国. 一个解析几何定点问题引发的思考[J].重庆工商大学学报(自然科学版),2016(6):51-56
ZENG C T,TAN W G. An Analysis of the Fixed Point Problem in Analytic Geometry [J]. Journal of Chongqing Technology and Business University (Natural Science Edition), 2016 (6): 51-56
