高度场八叉树的体特征表达算法

高艺，罗健欣，裘杭萍，唐斌，吴波

1.中国人民解放军陆军工程大学，南京210007

2.中国人民解放军61175部队

高度场八叉树的体特征表达算法

高艺1，2，罗健欣1，裘杭萍1，唐斌1，吴波1

1.中国人民解放军陆军工程大学，南京210007

2.中国人民解放军61175部队

1 引言

场景表达是可视化技术的一个重要分支，也是计算机图形学研究的热点。体特征表达是其中必不可少的一项内容，它直接体现了场景的细节及真实感，对用户理解环境、认知环境有着至关重要的作用。

当前，体特征表达主要采用网格模型或体素模型。

网格模型是采用隐式表面近似来表达三维物体的几何信息。网格数量越多，越接近于原始曲面，但绘制耗费的时间也随之增加。这使得网格模型仅适用于小规模对象的建模。当前，研究的主要问题集中在网格简化[1-2]，对模型中远离观察者或相对较小的区域进行简化，减少多边形的数量，降低渲染开销。常见的简化机制包括顶点聚类[3]、增量式简化、采样[4]和自适应细分[5]等四种机制。对拓扑简单、平滑的表面具有较好的效果，但对复杂的表面，要将多个表面用一个表面来表示常常涉及复杂的计算。

体素模型[6]在计算机处理能力有限的早期，在医学成像如断层扫描CT，核磁共振成像MRI等方面提供了极大的帮助。随着图形硬件的快速发展，体素模型再一次焕发活力。目前，研究的主要内容是如何组织体素数据，尽可能地跳过空体素，节省存储空间，提高空间检索的效率。

Laine与Karras[7]提出了有效的稀疏体素八叉树（Efficient Sparse Voxel Octree，ESVO），该方法为每一个栅格单元都提供一个过滤的轮廓近似，如果该轮廓可以很好地近似原始几何，则八叉树不需要进一步细分到更深的层次。这种表达方法对具有大量平坦表面的场景有很好的压缩性能，用近似轮廓在高分辨率下取代体素，能实现有效的存储压缩。Crassin等[8]注意到八叉树中具有自相似特性的特性可以合并，Kämpe[9]利用这一思想通过将稀疏八叉树转化为有向图（Directed Acyclic Graph，DAG）的方式实现了使用约1 GB内存对128K3解析率场景的建模。Villanueva[10]在此基础上提出了一种通过相似变换将八叉树的子节点合并，通过合并子树来实现无损压缩。

尽管如此，与高度场表达相比，网格表达和体素表达的存储量仍远高于高度场表达，且这两种模型的渲染都不易于移植到GPU中。

网格模型的渲染效率会受到三角形面片数量的影响，很容易达到GPU渲染管线的性能极限，还可能因面片太小而导致重采样的问题；体素模型因其三维的数据结构并不适合直接在GPU中进行快速地并行光线投射。

相反，高度场模型具有存储量较小，易于调度更新的优点，而且高度场数据可通过二维纹理的方式载入显存，在GPU中能获得极高的光线投射效率，性能优势明显[11-13]。但是，高度场不具备体特征表达的能力，在表达场景时通常采用法线贴图、视差贴图等技术对对象表面实施偏移操作，得到具有凹凸感的表面。这仅仅是一种增强视觉效果的2.5维表达，不是真三维体特征表达。目前的相关研究，高度场模型若要实现对真三维体特征表达，需辅以网格模型或体素模型才能实现[14-16]。在同一场景中使用不同类型的数据模型会增加系统的复杂度，降低渲染效率，在层次细节（LoD）更新、视点运动处理等方面都难以同步，对系统的图像质量有很大影响，影响用户体验。

基于上述讨论，本文提出了一种高度场八叉树的体特征表达算法。该算法既保留了传统高度场的优势，又解决了其体特征表达能力不足的问题。该算法的提出使得在同一个场景中可以使用统一的表达方式建模，为场景的体特征表达提供了一种新的可行途径。

2 基本原理

给出高度场八叉树的形式化描述如下：

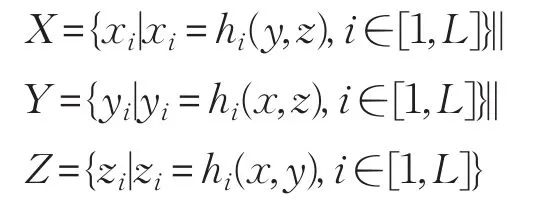
i表示当前八叉树子节点深度，L表示八叉树最大深度。

对图1（a）中的任意模型，传统的高度场z=h(x,y)是无法建模z方向上关于(x,y)的多值函数（图1（b））问题；图1（c）是体素八叉树模型示例，基于体素的场景则是由许多三维体素表示的空间。

高度场八叉树采用八叉树对三维模型进行树状细分，在八叉树的子节点内从三个坐标轴方向上判断是否存在高度场的单值函数，若在其中一个方向上存在单值函数即存在单一高度场，则在子节点中进行均匀离散采样，得到分布规则的高度场八叉树模型。图1（d）是一个高度场八叉树模型示例，八叉树不同层的高度场以不同的颜色进行标记区分，每层高度场的覆盖范围包含了从基平面到该层次表面所有的空间，各层叠加在一起构成了高度场八叉树结构。

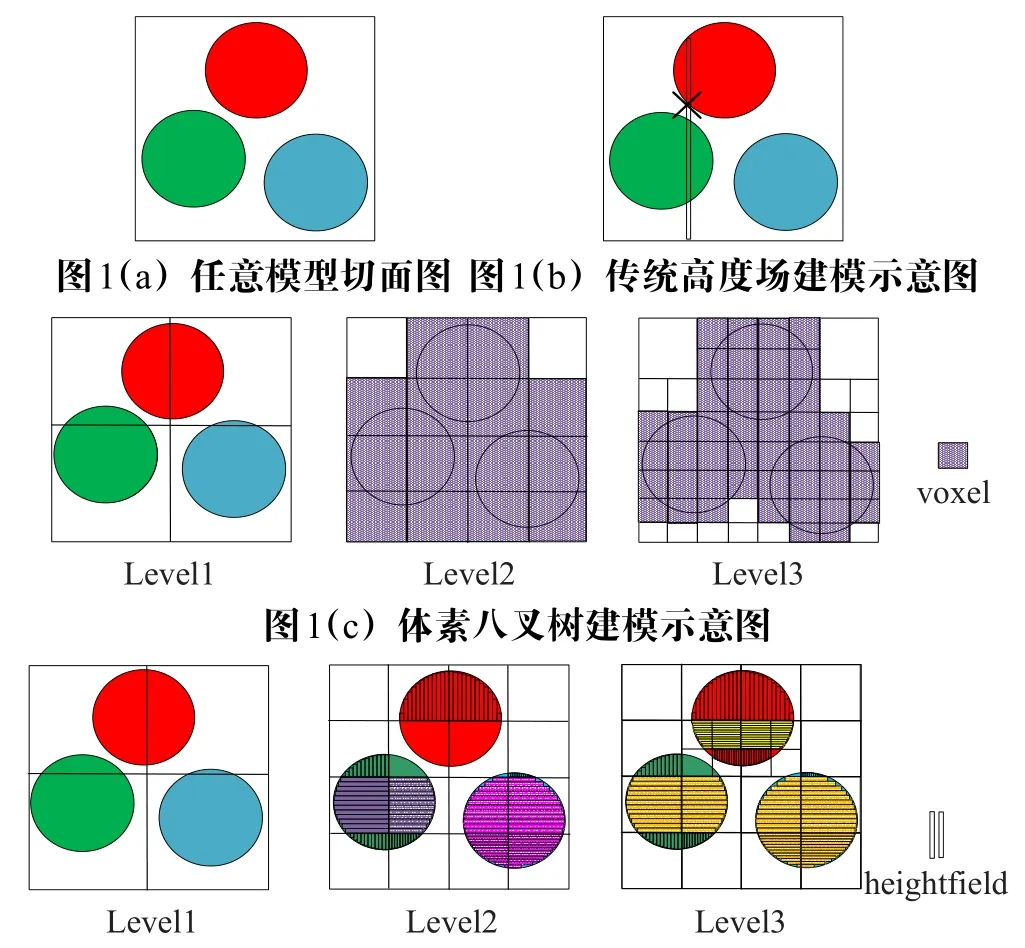
图1 （d）高度场八叉树建模示意图

与所有的节点都是基于八叉树细分的体素模型相比，八叉树高度场模型只需要少量的子节点就可以表达一个网格内的连续空间。

2.1 高度场八叉树约束体系

八叉树是组织三维模型的一种重要数据结构。树的根节点包含整个模型的数据及八个指针，每个指针指向一个子节点，每个节点关联一个与轴对齐的包围盒。传统八叉树子节点递归等分原则是八叉树结构达到最大深度或子节点中三角面片数小于设定的阈值，但本文的高度场八叉树约束体系是：

（1）八叉树节点的最大深度。

（2）子节点中所有三角面片可用高度场表示。

2.2 节点编码及类型

通常八叉树采用八进制Morton编码对节点进行编号，用0～7表示8个子节点的编号，在逐层构树中，节点编码的位数不断增加。

八叉树节点分为4个类型：内部节点、高度场节点、边界节点和空节点。内部节点为可剖分节点，有8个子节点；高度场节点为可剖分节点即叶节点，其所代表的空间满足约束体系（1）和（2），仅存储高度场数据及相应的参考平面信息；边界节点，其所代表的空间满足约束体系（1）但不满足约束体系（2）；空节点，其所代表的空间不包含三角面片。

2.3 算法流程

算法包含三个主要的阶段：一是三角面片预处理，二是判断是否存在单一高度场，三是高度场栅格化。算法流程如图2所示。

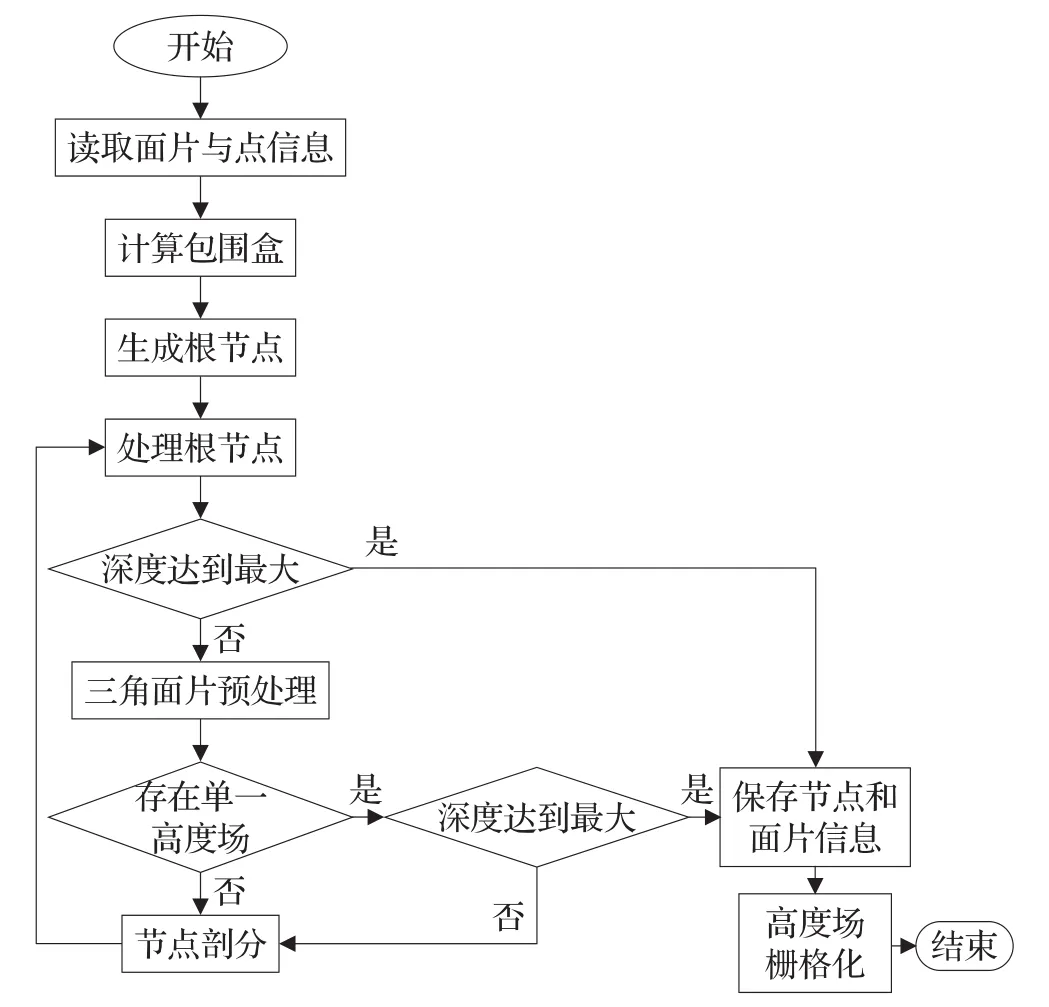
图2 算法流程图

3 空间高度场化

将三角面片表示的网格模型转换为二维的规则高度场并存储在3D纹理中的方法，即网格模型空间高度场化。提出了一个简单的高度场化方法，如图3所示。首先，对每一个三角面片进行空间几何求交，判断在三个坐标方向的相交性，然后，根据相交性确定不相交的坐标方向即为坐标轴主导轴，主导轴所对应的平面即为主导轴平面，最后栅格化后生成高度场数据及其他属性数据。

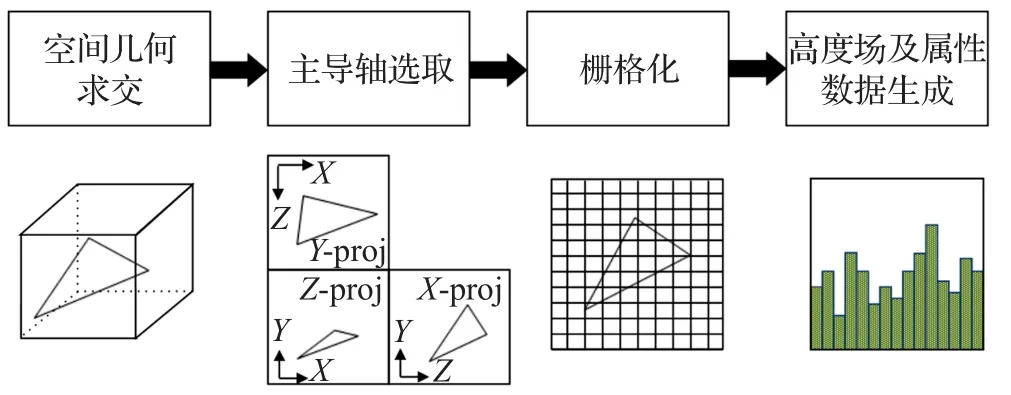
图3 高度场化管线流程

3.1 三角面片预处理

三角面片作为模型的基本图形单元，随着八叉树不断切分，与八叉树节点的一个或多个边界盒相交并衍生出新的三角面片。将其抽象化，即三角形边与边界盒平面的相交及交点计算。

如图4所示，三角面片（a）、（b）、（c）、（d）在父节点被剖分后，（b）、（c）、（d）与相应的子节点包围盒的不同平面相交并产生交点。

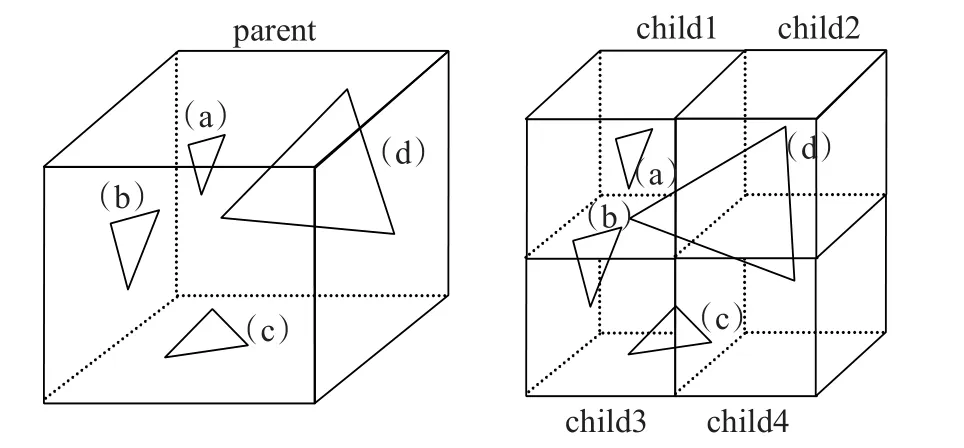
图4 八叉树父节点包含多个三角面片

将边界盒看作剖分区域，令待剖分的三角形网格模型为D，其顶点集和三角面片集为SV和ST，剖分后形成的三角形在剖分区域内为D+，在剖分区域外为D-，相应的顶点集和三角面片集分别记为VD+、TD+和VD-、TD-。令三角面片三个顶点(v1,v2,v3)所在剖分区域的Morton编码为m(vi)，Ti为该三角面片的面片集。

按如下方式对三角面片进行处理：

（1）三个m(vi)值相等，三角面片的三个顶点都在剖分区域内。如图5（a）（b）（c）所示，此种情况三角形没有被分割，因此在网格模型数据中保留，则；VD+=VD+⋃Vi，TD-=TD-⋃Ti。

（2）三个m(vi)值两两相等，三角面片两个顶点位于剖分区域内，一个节点在剖分区域外，此时参与求交运算的平面只有一个，需要分两种情况分别讨论。

如图5（d）所示，三角形一个顶点在相交平面上，其对边被剖切，此时原三角形被分割成两个三角形；如图5（e）所示，原三角形被剖分成一个四边形和一个三角形，四边形将根据对角线的长度，取较大的对角线为新三角形的边，剖分为两个新的三角形。原三角形在网格模型数据中删除，新增的三角形面片及其顶点信息添加到VD+、TD+和VD-、TD-中继续参与到下一层八叉树剖分。

（3）三个m(vi)值均不等，三角面片一个顶点位于剖分区域内，另两个顶点分别位于剖分区域外两个不同的节点。如图5（f）所示，相对于剖分区域而言，参与求交运算的平面有两个，此时原三角形被分割为多个三角形，与上相同，新增的三角形面片及其顶点信息添加到VD+、TD+和VD-、TD-中继续参与到下一层八叉树剖分。

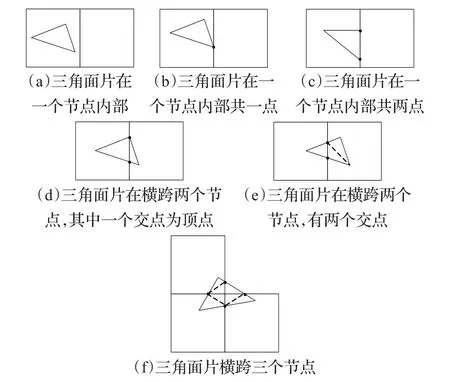
图5 三角面片的三个顶点与边界盒平面的相交关系

算法直接在三角网格模型的三角面片上实现剖分，经过预处理后，模型依然保持网格拓扑信息的有效性，同时也保证了网格数据的完整性。

3.2 空间几何求交

空间几何求交的目的是判断能否转换成空间高度场的依据。若存在单一高度场，则该子节点内包含的所有三角面片将被高度场化；若不存在单一高度场，则当前子节点内所有三角面片仍将继续参与剖分，直到能被高度场化为止。对空间几何求交这一问题的求解通常采用降维计算，将几何图元转换到相应的局部坐标系下，建立空间几何与平面图形间的映射关系，从而将三维的空间问题降为二维的平面问题，这是将复杂问题简单化的一种有效方式。空间几何的求交算法可简单表述如下：

步骤1根据参与运算几何图元的性质，构造局部坐标系。以XZ平面为例，平面方程为ax+by+cz+d=0。O是平面中心点，E是体边界盒的角点，EO单位向量为n1(a1,b1,c1),平面法向量n2,第三个向量n3=n1×n2。三个互相垂直的单位向量n1，n2，n3构成局部坐标投影系。如图6所示。

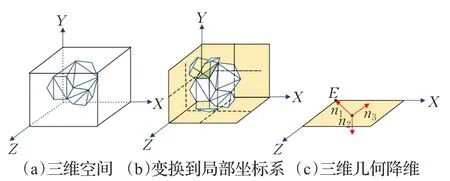
图6 空间几何相交问题的降维过程

步骤2应用2D/3D对应理论建立空间几何图元降维前后的计算关系，形成投影面上的计算方案。

设顶点坐标为(x,y,z)的空间三角形，变换到局部坐标下的坐标为(x′,y′,z′)，其满足(x'y'z'1)=(xyz1)PTT，其中P是投影矩阵，T是变换矩阵，如下式所示：

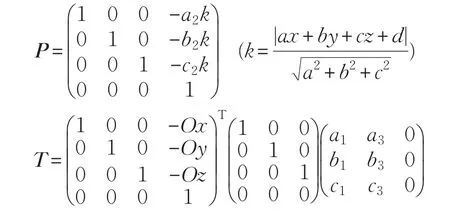
3.3 主导轴选取

定义三个坐标方向索引值，0为XY坐标方向，1为ZY坐标方向，2为XZ坐标方向，依次遍历节点中的所有几何图元，向三个方向的任一平面做投影降维。经过投影降维后的几何图元（三角面片）在二维平面上分别进行相交关系的判断，如果投影三角面片互不相交，则该投影方向即为主导轴，该轴对应的平面即为参考平面。对于二维平面的判交已有成熟的研究[17]，本文不再赘述。

3.4 栅格化及数据生成

每一个三角片和其所在的参考平面将一起输入到栅格化管线中。在栅格化的过程中，每一个三角面片都会生成一系列的2D片元，每一个片元都与主导轴相关联，计算插值后的三角形顶点到主导轴平面的距离，这样的2D片元即为高度场数据片元。

高度场数据通常包含高度值数据，还包含一些属性数据如：颜色、法线以及在实际应用中所需的其他有用信息如材质等。这些值或许是从顶点属性像素中插值得到，或许是从模型的2D表面纹理得到，最后会被写入到3D纹理中。

整个空间高度场化的过程只有空间几何求交部分在CPU中实现，其余过程均在GPU中实现，尽管CPU和GPU之间的通信会造成一定的时间耗费，但比起在CPU中已经极大地提升了执行效率。

4 高度场八叉树光线投射

目前，高度场渲染从技术的角度来分，可以分为两种：一种是将高度场转换为三角形网格，用硬件渲染三角网格即基于高度场的光栅化方法。用GPU进行渲染时，需要将三角形面片发送至GPU的显存中，而CPU与GPU之间进行数据交换的代价比较高，大量的数据发送必将导致很高的渲染耗时，降低系统性能。一种是使用光线投射直接渲染高度场，其优点一是表达方式更简洁，有较低的内存要求；二是对于大规模高度场数据集来说，光线追踪是一个图像的顺序算法，本质上忽略了高度场的遮挡区域；三是高度场包含多个对象的表示，包括几何、体积、全局光照效果如反射、折射、软阴影等。

早期的高度场光线投射算法都在CPU中执行，由于CPU的串行工作方式，算法只能逐光线渲染，渲染效率很低。随着图形硬件突飞猛进的发展，显卡的处理能力不再是性能提升的瓶颈，基于GPU光线高度场光线投射算法再一次受到了重视。现有的基于GPU高度场光线投射算法都是传统的单层高度场，因此是在z-xoy坐标系中，以地面（xoy）作为参考平面，模型被看做各空间位置相对于z平面的距离值集合，在光线迭代时，使用如下公式进行相交测试：

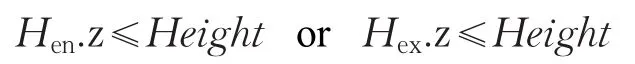
式中，Hen为光线进入单元边界处坐标，Hex为光线离开单元边界处坐标，Height为光线进入的单元高度。如图7所示[18]。

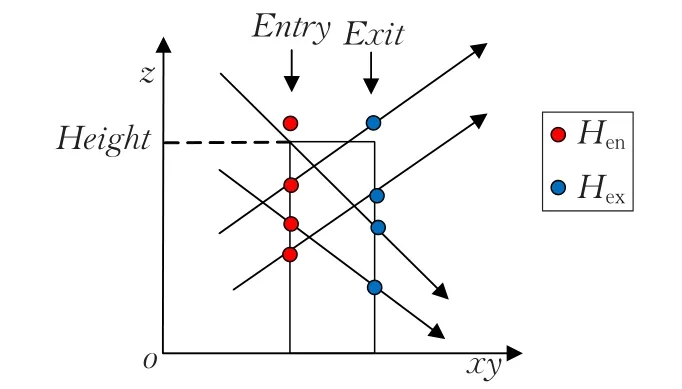
图7 传统的高度场光线投射光线与模型相交关系

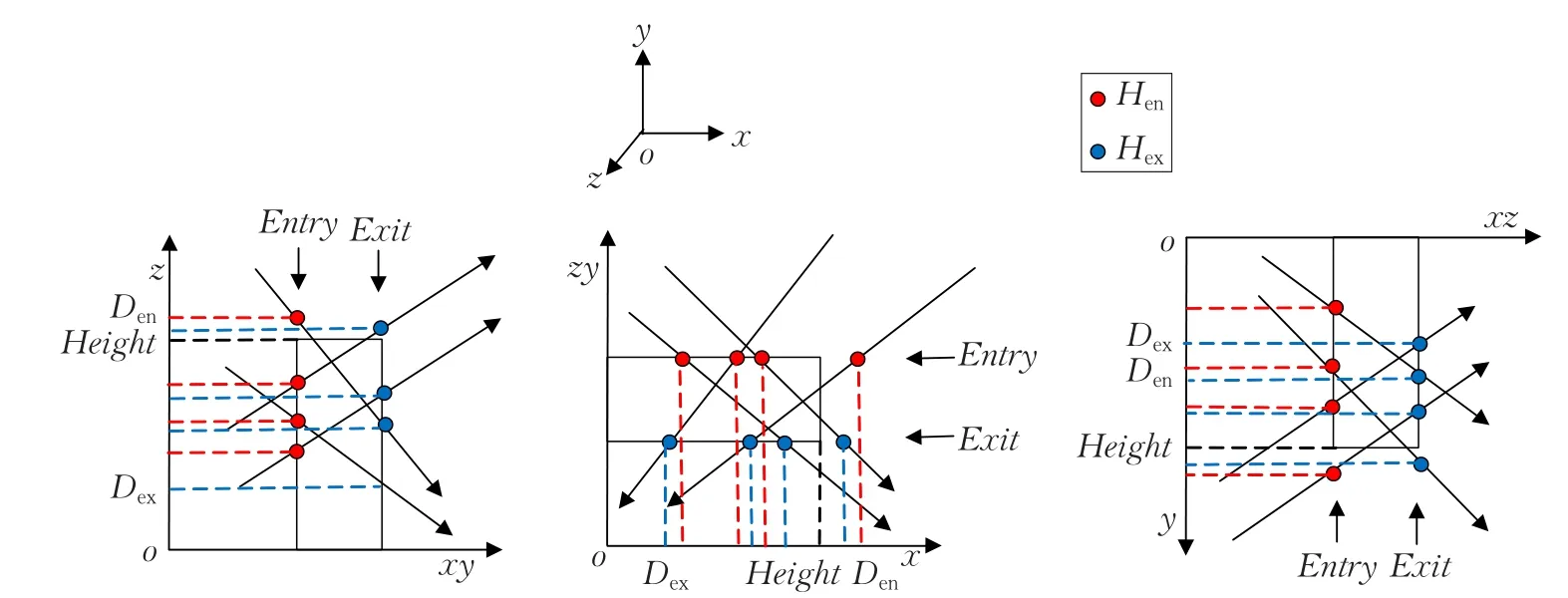
图8 高度场八叉树光线投射光线与模型相交关系

在本文的高度场八叉树中，高度场在空间中不再只是z=f(x,y)函数，还可能是y=f(x,z)或x=f(y,z)的函数，坐标系不同，相交规则也不同，因此重新定义相交规则如下式：

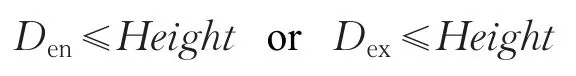
式中，Den=dist(Hen,plane)为光线进入单元边界处到参考平面的距离，Dex=dist(Hex,plane)为光线离开单元边界处参考平面的距离。如图8所示。

光线在不同的参考平面上迭代，逐像素步进，在每个迭代位置，使用公式进行相交测试，若相交则输出当前交点的颜色纹理，渲染在屏幕上。

5 实验与分析

实验使用C++与GLSL语言，在Microsoft Windows 7操作系统，OpenGL4.4.0上实现。实验环境为Inter®CoreTMi5-3337U处理器，4 GB内存。显卡为NVIDIA GeForce GT 620M。

为了验证本文所述的稀疏空间高度场的表达能力及对所述模型算法进行重现验证，实验所用的数据来自NVIDIA SDK的Venusm模型、Lady和Rabbit三维模型。

图9是不同分辨率下的Venusm模型渲染效果对比。从对比图可知，Venusm模型场景分辨率为1 024×1 024时即可以得到质量较高的图像。

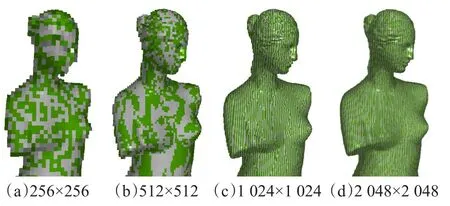
图9 基于稀疏空间高度场的Venusm模型在不同分辨率下的效果对比

表1给出了本文所用的模型参数和测试结果，在不同的分辨率下，对比了使用SVO和使用本文高度场八叉树进行建模时两者的占用存储空间对比。从表1可知，使用高度场八叉树在相同的分辨率情况下比SVO占用了更小的存储空间。因为随着分辨率的不断提高，SVO除空节点外的每一个节点都有8个子节点，而高度场八叉树中，只要存在单一高度场的节点将不再产生子节点。

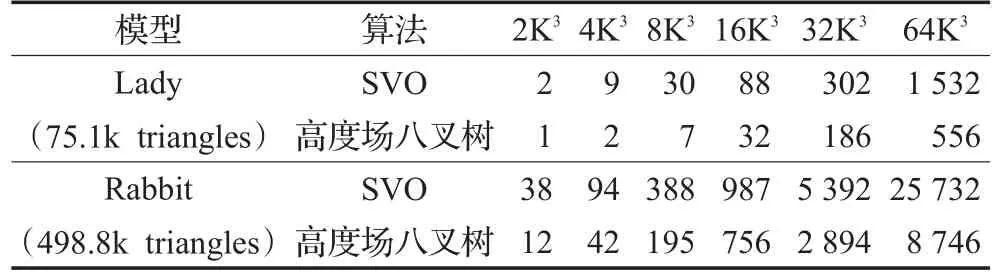
表1 不同分辨率下规则八叉树与本文算法占用存储空间对比MB

图10是使用SVO和高度场八叉树的模型结构图及参考平面（绿色）。从图10可知，在树深度相同的情况下，SVO生成的模型几乎被八叉树的子节点块完全覆盖，而本文算法在相对平坦（如兔子的腹部）或相对对称（如人的腰部和腿部）的部分能快速地找到单一高度场，具有更少的节点数。

图10 （a）最大深度为8的SVO结构图

图10 （b）最大深度为8的高度场八叉树结构图

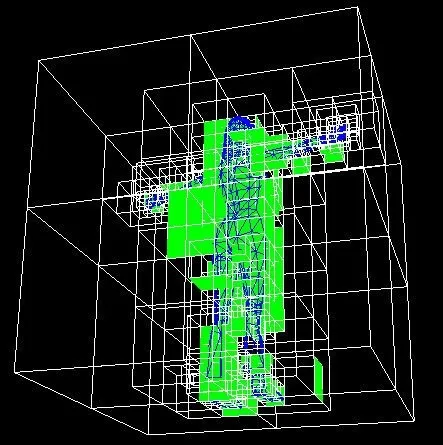
图10 （c）深度5时的单一高度场参考平面

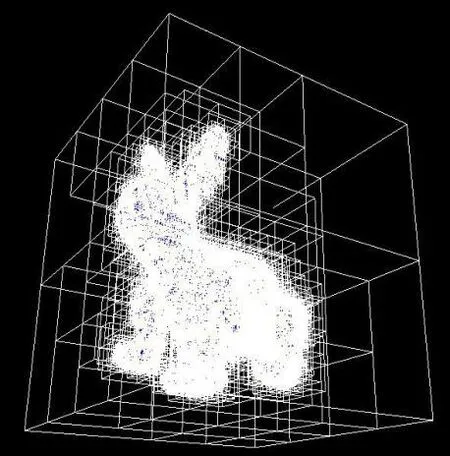
图10 （d）最大深度为8的SVO结构图

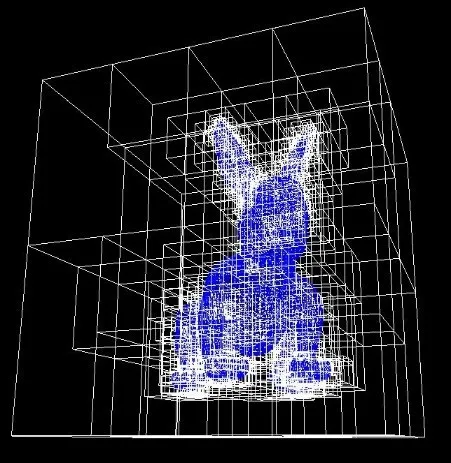
图10 （e）最大深度为8的高度场八叉树结构图

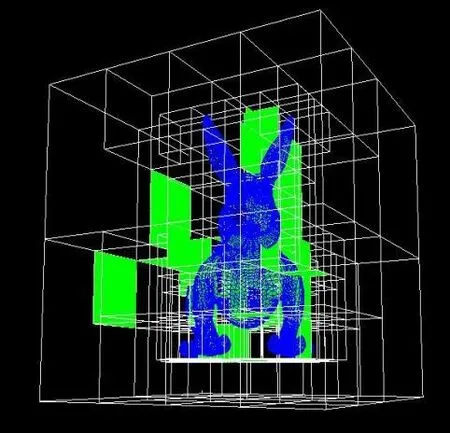
图10 （f）深度3时的单一高度场参考平面

图11是平面分辨率为4 096×4 096的Lady模型，在本文算法与文献[7]算法下的光线投射帧速率对比。图中横坐标为渲染过程中的时间记录，纵坐标为记录的帧速率。根据帧速率公式[19]：

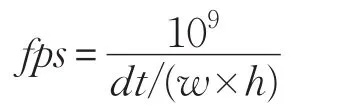
dt为帧时间，w×h为屏幕分辨率，文献[7]的平均帧速率大约为55帧/s，而高度场八叉树的平均帧速率大约为83帧/s，本文算法具有更高的光线投射效率。

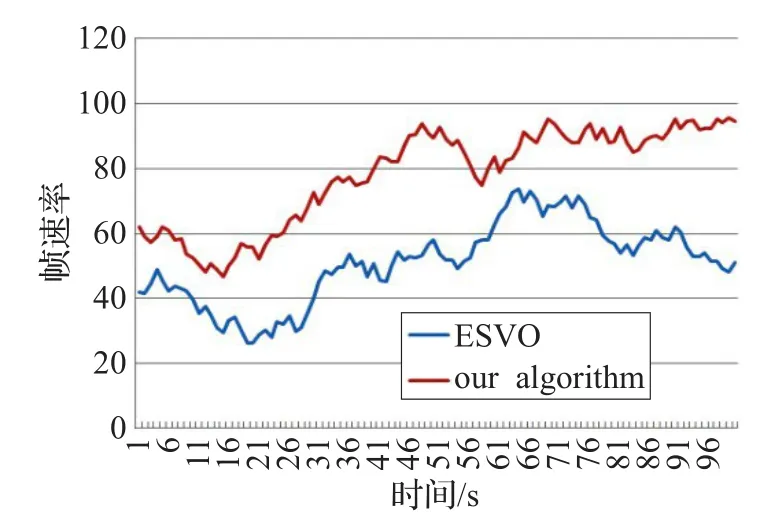
图11 两种算法的光线投射效率对比

6 结束语

本文提出了一种基于高度场八叉树的体特征表达算法。算法将传统的z向高度场扩展到了x、y、z三个方向的高度场，借助八叉树的空间分割，使得高度场具备了体特征表达的能力。与体素八叉树表达相比，高度场八叉树和体素八叉树一样，都是基于三维的空间网格结构，但高度场八叉树的子节点是一个二维空间的高度场数据，而体素八叉树的子节点是一个三维空间的体素数据，这使得高度场八叉树在存储空间和光线投射效率上都比体素八叉树更有优势，实验结果也进一步证明了算法的有效性。因此，本文算法在保持传统高度场表达优势的同时，又解决了传统高度场体特征表达能力不足的问题。

本文提出的算法还有需要优化的方向：一是算法没有考虑极端复杂的模型，对于已经达到树最大深度，仍然未找到高度场的节点采用网格模型渲染，下一步可以在此类节点中对高度场分层，形成层次高度场；二是八叉树的构建过程需要不断地进行三角面片剖分及相交判断，影响了建树的时间，下一步在GPU中实现这一过程，可以很好地解决这一问题。

[1] Kumar S，Manocha D.Interactive display of large scale trimmed NURBS models[R].University of North Carolina at Chapel Hill，1994.

[2] 韩敏，陈鸿博，郑丹晨.基于分块Morton压缩和混合生成准则的地形简化方法[J].计算机辅助设计与图形学学报，2014，26（2）：293-301.

[3] 郭力真，吴恩华.多边形模型简化算法综述[J].计算机应用研究，2005，22（8）：20-23.

[4] Akeley K.Reality engine graphics[C]//Proceedings of the 20th Annual Conference on Computer Graphics and Interactive Techniques，1993：109-116.

[5] Whitted T.An improved illumination model for shaded display[J].Communications of the ACM，1980，23：343-349.

[6] Kaufman A，Shimony E.3D scan-conversion algorithms for voxel-based graphics[C]//Proceedings of the 1986 Workshop on Interactive 3D Graphics，1987：45-75.

[7] Laine S，Karras T.Efficient sparse voxel octrees[J].IEEE Transactions on Visualization and Computer Graphics，2011，17（8）：1048-1059.

[8] Crassin C，Neyret F，Sainz M，et al.Interactive indirect illumination using voxel cone tracing[J].Computer Graphics Forum，2011，30（7）：1921-1930.

[9] Kämpe V，Sintorn E，Assarsson U.High resolution sparse voxel DAGs[J].ACM Transactions on Graphics，2013，32（4）：101.

[10] Villanueva A J，Marton F，Gobbetti E.SSVDAGs：Symmetryaware sparse voxel DAGs[C]//Proceedings of the 20th ACM SIGGRAPH Symposium on Interactive 3D Graphics and Games，2016：7-14.

[11] Zhai R，Lu K，Pan W，et al.GPU-based real-time terrain rendering：Design and implementation[J].Neurocomputing，2016，171（C）：1-8.

[12] 罗健欣，胡谷雨，倪桂强.平行流形空间光线投射高度场可视化算法[J].计算机辅助设计与图形学学报，2013，25（3）：356-362.

[13] Luo J，Hu G，Ni G.Dual-space ray casting for height fieldrendering[J].ComputerAnimationandVirtual Worlds，2014，25（1）：45-56.

[14] Paredes E G，Amor M，Bóo M，et al.Hybrid terrain rendering based on the external edge primitive[J].International Journal of Geographical Information Science，2016，30（6）：1095-1116.

[15] Ammann L，Dischler J M.Hybrid rendering of dynamic heightfields using ray-casting and mesh rasterization[C]//Graphics Interface.[S.l.]：Canadian Information Processing Society，2010：161-168.

[16] Koca Ç，Güdükbay U.A hybrid representation for modeling，interactive editing，and real-time visualization of terrains with volumetric features[J].International Journal of Geographical Information Science，2014，28（9）：1821-1847.

[17] 于海燕，何援军.空间两三角形的相交问题[J].图学学报，2013，34（4）：54-62.

[18] Luo J，Ni G，Cui P，et al.Quad-tree atlas ray casting：A GPU based framework for terrain visualization and its applications[M]//TransactionsonEdutainmentVII.Berlin Heidelberg：Springer，2012：74-85.

[19] van Wingerden T L.Real-time ray tracing and editing of large voxel scenes[D].Utrecht University，2015.

GAO Yi,LUO Jianxin,QIU Hangping,et al.Volumetric features representation algorithm using heightfields-octree.Computer Engineering andApplications,2018,54（6）：1-6.

GAO Yi1，2,LUO Jianxin1,QIU Hangping1,TANG Bin1,WU Bo1

1.PLAArmy Engineering University,Nanjing 210007,China
2.PLATroops of 61175,China

Volumetric features representation plays a vital role for user understanding and recognizing the virtual environment.The current algorithm is inefficient due to its large storage and inconvenient acceleration in GPU,and it is difficult to satisfy the real-time requirements of visualization.Aiming at this problem,an efficient volumetric features representation algorithm using heightfields-octree is proposed.The algorithm can not only solve the problem that the heightfields can only represent 2.5 dimensional scene,and cannot express the true 3 dimensional scene,but also provide a new feasible way for volumetric features representation.The heightfields representation of 3D scene is generated by octree structure,which extends the traditional heightfields of z to x,y and z three directions.Firstly,a preprocessing method of triangular is put forward,ensuring model accuracy and data integrity.Secondly,an algorithm of heightfields judgment and rasterization on projection transformation is proposed,converting geometric primitives into heightfields of two-dimensional space.Finally,the ray casting algorithm based on heightfields octree is realized.The experimental results show that the algorithm can dramatically reduce data storage capacity,and higher ray casting efficiency,and better expression of 3 dimensional scene.

volumetric features representation;heightfields-octree;projection transformation;ray casting

体特征表达对用户理解和认知虚拟环境有着至关重要的作用。当前的体特征表达算法由于存储量大且不易于在GPU中加速等问题，渲染效率低下，难以满足场景可视化的实时性需求。针对这一问题，提出了一种高效的高度场八叉树体特征表达算法，不仅解决了传统高度场仅能表达2.5维模型，无法表达真三维模型的问题，而且为体特征表达提供了一种新的可行途径。算法使用八叉树结构生成三维模型的高度场表示，将传统的z向高度场扩展到x，y，z三个方向的高度场。首先，提出了三角面片预处理方法，保证模型精度和数据的完整性;其次，提出了基于投影变换的高度场表示判断及栅格化方法，将几何图元转换成二维空间的高度场数据;最后，提出了基于高度场八叉树的光线投射算法。实验结果表明，算法能极大地减少存储量，具有较高的光线投射效率，表达三维模型时取得较好效果。

体特征表达；高度场八叉树；投影变换；光线投射

2017-11-17

2018-01-26

1002-8331（2018）06-0001-06

A

TP393

10.3778/j.issn.1002-8331.1711-0245

国家部委科技基金；江苏省青年科学基金（No.BK20150722）。

高艺（1982—），女，博士研究生，工程师，主要研究方向为虚拟现实与仿真，E-mail：iamninigao@163.com；罗健欣（1984—），男，博士，讲师，主要研究方向为计算机图形与图像处理；裘杭萍（1965—），女，博士，教授，主要研究方向为系统工程；唐斌（1986—），男，博士，主要研究方向为计算机图形与图像处理；吴波（1977—），男，讲师，主要研究方向为系统工程。