基于附加效应的设计过程复杂性分析过程模型

张 鹏,张建辉,董娅凡,张换高+,檀润华

(1.河北工业大学 机械工程学院;2.国家技术创新方法与实施工具工程技术研究中心,天津 300130)

0 引言

随着用户需求的提高，工程系统日趋复杂，复杂机电系统的开放性、非线性和时变特性显著增强，系统中功能之间的耦合关系更加强烈，因此复杂机电系统的研究成为热点。目前国内外很多学者应用设计过程复杂性(Design-Centric Complexity, DCC)理论[1]对复杂机电系统进行了研究。DDC研究源于Suh有关设计方面复杂性的专著[2]，DCC理论从功能的角度分析解决系统中的复杂性，其中的复杂性被定义为实现功能需求不确定的程度，功能需求实现概率的高低是衡量系统是否复杂的唯一标准；除此之外，该理论还对系统中存在的DDC进行了分类，并讨论了减小DDC的方法。Lu等[3]针对设计决策的主观性和客观性，探讨了设计决策主观性对系统DDC的影响，即在同一系统中，优良的设计决策系统的DDC为有限值，系统的功能需求可以实现，而不良的设计决策会导致系统中的DDC趋于无限，系统的功能需求无法实现，因此不同的设计决策会导致系统的DDC存在明显的差异；Suh[4]提出功能周期的概念，建立系统的功能周期是实现系统长期稳定的基础，是降低系统DDC的重要途径；Suh等[4]指出，将系统中的时间相关组合复杂性转换为时间相关周期复杂性可以提高系统功能的实现概率；文献[6-7]分别针对具有时变特征的混合装配系统和成长型组织系统研究其DDC降低方法，表明DDC理论具备分析复杂机电系统时变特性的能力。非线性和耦合特性也是复杂机电系统重要的特征，张鹏等[8-9]提出一种基于DDC理论的冲突确定过程模型，冲突表达了系统参数的耦合关系，是系统非线性的体现，意味着DDC理论可以表征复杂机电系统的非线性和耦合特性。除了上述复杂机电系的统特征，作为复杂机电系统中的重要特征之一，开放性与DDC之间的关系还没有进行相关研究。

DDC理论建立了用户需求、功能及其结构的映射关系，并用设计矩阵A表达其映射关系，对于可还原的简单系统，这种方法是行之有效的。然而，系统功能中的严重耦合和非线性，特别是与超系统严重的耦合和非线性，即复杂机电系统的开放性不能体现在设计矩阵A中。为了应用DDC理论分析复杂机电系统的开放性，将设计矩阵A扩展为广义设计矩阵As，As不但表达了设计参数之间的关系，而且表达了超系统对系统的影响。DDC理论是从功能的视角考虑系统中存在的复杂性问题，作为实现相应功能的科学原理，效应体现了功能与参数之间的关系，其中设计需求与设计参数之间的关系定义为理想效应(ideal effect)，超系统对系统的影响定义为附加效应(additional effect)。用功能需求—设计矩阵—理想效应表达系统的设计要求，功能需求—广义设计矩阵—附加效应表达系统中存在的超系统影响以及耦合性和非线性。广义矩阵As表达了系统和超系统的参数与功能之间的关系，其中理想效应表达功能需求，附加效应表达系统和超系统之间的耦合、非线性和开放性，形成基于附加效应的DDC分析过程模型。最后，用一个工程实例对该设计过程模型进行了验证。

1 设计过程复杂性理论

复杂性是实现功能需求不确定性的程度[10]。在给定的精度或公差范围内确定满足功能需求的设计参数后，系统实现功能需求的概率能够表征系统的复杂性，其值越高，系统的复杂性越低，其值越低，系统的复杂性越高。复杂性是设计范围与系统范围之间关系的函数，如图1所示[10]。

系统功能需求函数与共同范围所围成的面积Acr，表示设计实现特定目标的可能，即信息含量[10]，表示为

复杂机电系统的功能实现概率可以用设计过程复杂性，即信息含量描述。DDC理论用设计矩阵建立了功能和参数之间的关系，然而这些参数均与系统功能对应，无法体现复杂机电系统的开放性这一重要特征，对复杂机电系统的非线性、时变特性和耦合性体现不足。效应可以为系统的功能及其对应参数建立的联系，附加效应则可表达导致系统出现设计过程复杂性的功能，实现对系统开放性、非线性、时变特性和耦合性的表达。下面介绍效应、理想效应和附加效应的定义及其关系。

2 效应与附加效应

效应[11]是一种基础的知识工具，其将物理、化学、几何等科学原理与其工程应用有机结合在一起，消除了科学与工程应用之间的隔阂。效应为系统的DDC和功能需求建立了联系，一方面效应是系统功能需求实现的基础，与系统的功能有对应关系；另一方面，效应的输入流、控制流和输出流直接与设计参数有关，可以用于明晰导致设计过程复杂性的参数，以效应为桥梁建立复杂机电系统功能和对应参数之间的关系，不但可以体现系统内各个功能之间耦合情况，而且可以准确表达超系统对复杂机电系统的影响，开放性、非线性、耦合性和时变特性等复杂机电系统特性都能在效应对应的参数中得到体现。

为了区别复杂机电系统中体现实现功能需求的效应和导致系统出现设计过程复杂性的效应，将效应分为理想效应和附加效应，其中实现功能需求的效应称为理想效应，导致系统存在设计过程复杂性的效应称为附加效应。

2.1 理想效应和附加效应

理想效应和附加效应是应用效应分析系统DDC的两个重要的概念。

定义1理想效应指在预期的输入流、输出流和控制流作用下，以预期的因果关系实现系统功能需求的效应。理想效应表达了功能需求与参数之间的关系，体现的是系统的预期功能和有用功能。

Ideal Effect=IWi,IWc,IWo。

式中:Ideal Effect为理想效应；IWi为预期输入流；IWo为预期输出流；IWc为预期控制流。

定义2附加效应指一些非预期的输入流、输出流和控制流与预期的输入流、输出流和控制流之间相互影响，导致理想效应预期的因果关系和系统功能需求无法实现的效应。附加效应表达了非预期参数对功能的影响，是复杂系统功能耦合、非线性和超系统影响效应的表达，体现的是系统的非预期功能和有害功能。

式中:Additional Effect为附加效应；AWi为非预期输入流；AWo为非预期输出流；AWc为非预期控制流。

系统的功能需求可以用一组理想效应表示，由于系统中功能之间的耦合、环境影响及一些其他随机变量的影响，系统的功能需求无法得到满足，导致系统存在设计过程复杂性，这些影响系统功能实现的因素以附加效应的形式存在于系统中。

系统中包含多个功能需求，系统理想效应之和表示总功能需求，如式(1)所示;系统的所有理想效应与所有附加效应之和表示系统当前的总功能，如式(2)所示。

FR=∑E;

(1)

F=∑E+∑Ea。

(2)

式中：∑E表示功能的理想效应实现；∑Ea表示功能的附加效应实现。

因为附加效应影响系统功能需求的方式不尽相同，所以结合附加效应的定义讨论附加效应的分类方法。

2.2 附加效应的种类

附加效应从输入流、输出流和控制流3个方面影响理想效应。综合考虑附加效应提供的非预期输入流、输出流和控制流对理想效应预期输入流、输出流和控制流的影响的统一效应称为扩展效应，

E Effect=Wi(IWi，AWi),

式中E Effect为扩展效应。

扩展效应模型如图2所示。

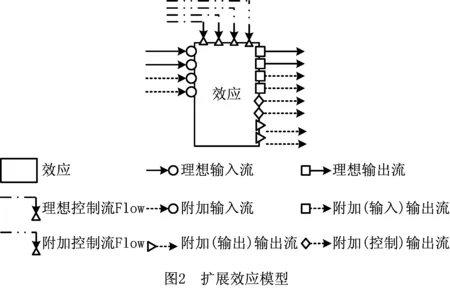
附加效应的分类如下：

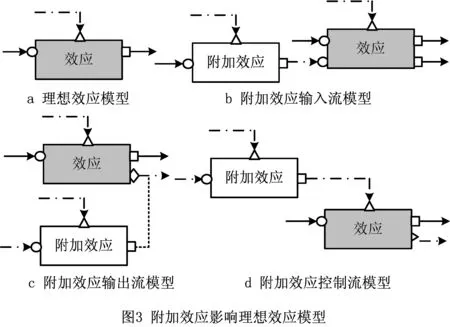
(1)产生附加效应的因素很多，按照附加效应影响理想效应的方式，附加效应有3种模型,如图3所示。其中图3a为理想效应模型，图3b为附加效应影响理想效应输入流模型，附加效应为理想效应提供了一个非预期的输入流，导致理想效应输出了一个非预期的输出流；图3c为附加效应影响理想效应输出模型，附加效应为理想效应提供了一个非预期的输出流，该输出流导致理想效应输出了一个非预期的输出流；类似地，图3d为附加效应影响理想效应控制流模型，附加效应为理想效应提供了一个非预期的控制流，该控制流导致理想效应输出了一个非预期的输出流。

(2)产生附加效应的来源有系统内部因素影响和超系统(系统外部)因素影响两种。根据附加效应影响理想效应模型及附加效应的来源，将系统中可能存在的附加效应分为6种，即系统内附加效应影响输入流型、系统内附加效应影响输出流型、系统内附加效应影响控制流型、超系统附加效应影响输入流型、超系统附加效应影响输出流型和超系统附加效应影响控制流型。附加效应的分类如图4所示。

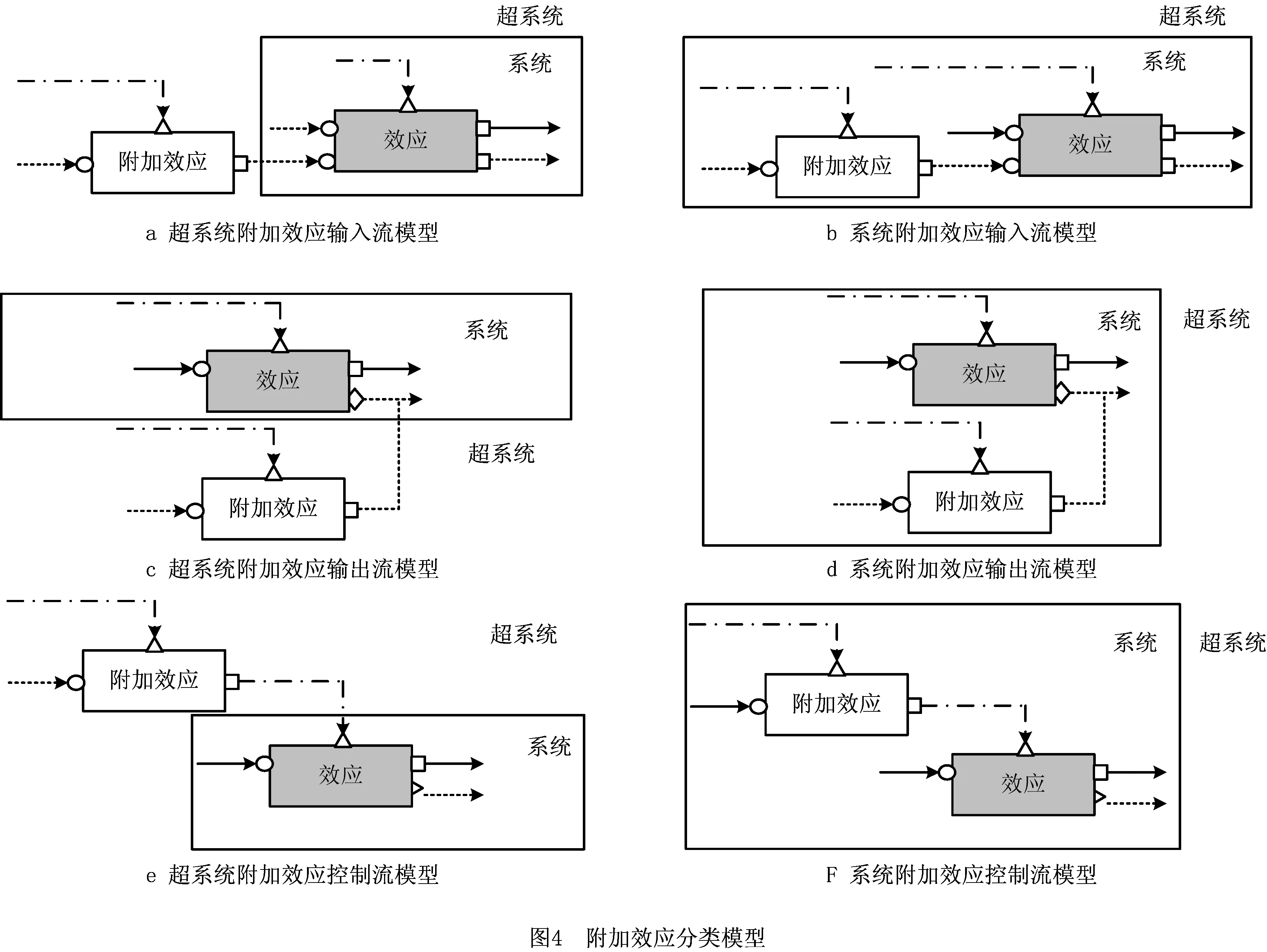
6种模型分别描述如下：

(1)系统内附加效应影响输入型

E Effect=Wi(IWi，AWi),Wc(IWc),

(2)系统内附加效应影响输出型

E Effect=Wi(IWi),Wc(IWc),

(3)系统内附加效应禁止输出型

E Effect=Wi(IWi),Wc(IWc，AWc),

(4)系统内附加效应影响输入型

E Effect=Wi(IWi，AWi),Wc(IWc),

(5)系统内附加效应影响输出型

E Effect=Wi(IWi),Wc(IWc),

(6)系统内附加效应禁止输出型

E Effect=Wi(IWi),Wc(IWc，AWc),

根据6种附加效应导致系统出现的复杂性，系统的复杂性统一模型可以描述为

E Effect=Wi(IWi，AWi),Wc(IWc，AWc),

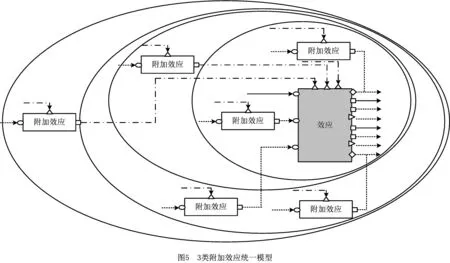
根据系统附加效应的求解难度，进一步将6个模型分为3类，如图5所示。

(1)系统内部附加效应对理想效应的影响 这类附加效应的影响表现为系统内效应影响理想效应的输入和输出，体现为系统功能需求之间耦合导致的设计过程复杂性。

(2)超系统的附加效应对系统理想效应的影响 这种附加效应表现为超系统的附加效应对系统内理想效应输入和输出的影响，由超系统对系统参数的影响导致，不是系统内功能耦合造成的，体现了复杂机电系统的开放性。

(3)超系统的的附加效应使理想效应失效 当这种附加效应存在时，系统的理想效应会失效。

3类附加效应影响系统理想效应的统一模型如图5所示。以上3类附加效应的分类是在附加效应与相应的理想效应不同名的基础上进行的。当附加效应与理想效应同名且其相应的输入流、输出流和控制流存在一定关系时，还存在一种特殊的附加效应——同名附加效应，即第4类附加效应,这类效应被用来实现功能需求，但却不能完全实现系统所需的功能需求。

同名附加效应指附加效应与理想效应名称相同，且其相应的输入流、输出流和控制流存在一定关系。同名附加效应包括同名附加效应影响输入型、同名附加效应影响输出型和同名附加效应禁止输出型3个类型，分别表示为：

E Effect=Wi((I+A)Wi),Wc(IWc),

因此，同名附加效应导致系统出现复杂性的统一模型可以描述为

E Effect=Wi((I+A)Wi),Wc((I+A)Wc),

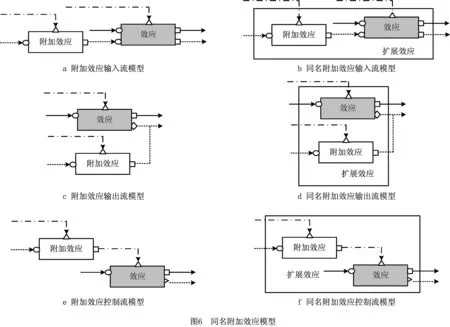
由于同名附加效应与系统中相应的理想效应同名，当理想效应的输入流、输出流和控制流发生变化时，同名附加效应的输入流、输出流和控制流也会发生相应的变化。而同名附加效应的这些变化会直接影响到该理想效应所实现的功能的概率。例如图6a所示为附加效应输入流模型，表示附加效应对理想效应输入流的影响，当该附加效应为同名附加效应时，该模型可以转化为如图6b所示的同名附加效应输入流模型。在图6b中，同名附加效应和理想效应可以由一个扩展效应表示，且该扩展效应与图中的理想效应和附加效应也同名，称为同名扩展效应。在同名扩展效应中，理想效应和附加效应的输入流共同作为同名扩展效应的输入流，理想效应和附加效应的控制流共同作为同名扩展效应的控制流。通过图6b可以看出，当同名扩展效应的输入为理想效应的输入流，且同名扩展效应的控制流为理想效应的控制流时，附加效应的输出流为0，同名扩展效应的输出流由理想效应的输出流决定。当同名扩展效应的输入流(或为控制流)发生变化时，其输出流由理想效应和附加效应共同决定，即在同名扩展效应中，附加效应随理想效应的变化而变化，当附加效应的输出减小或增大时，理想效应的输出流将随之减小或增大，因此单独去除附加效应的影响比较困难。类似地，图6c表示了附加效应输出流模型，如果附加效应与理想效应同名并影响理想效应的输出，则可以得到如图6d所示的同名附加效应输出流模型；由图6e所示的附加效应控制流模型，也可以得到图6f所示的同名附加效应控制流模型。由于同名附加效应与相应的理想效应存在紧密关系，单独消除其对理想效应的影响非常困难。为了方便分析这种同名附加效应，单独将其定义为附加效应中的一类，称为第4类附加效应。

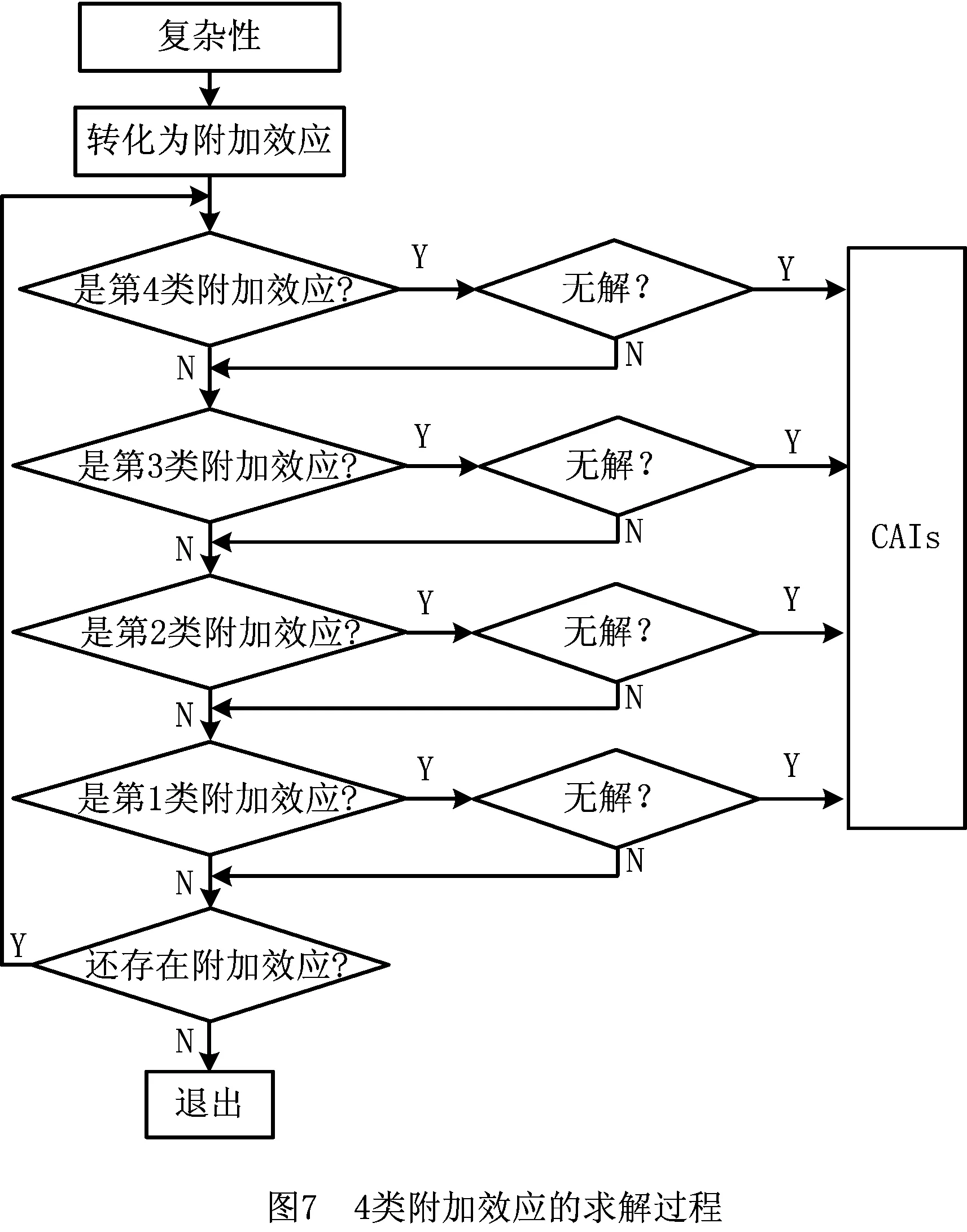
对于一些离散的附加效应，即为组成附加效应链的附加效应，在其求解过程中，由于同名附加效应(即第4类附加效应)与理想效应存在密切的关系，当同名附加效应影响系统功能实现概率时，应首先对其进行求解。在求解同名附加效应的过程中，可能改变系统原有的理想效应，而理想效应的变化可能直接导致系统附加效应发生变化。当系统中不存在同名附加效应时，应该对其他3类附加效应进行求解，从这3类附加效应的定义及分析工具可以看出，第3类附加效应的求解最困难，第2类附加效应次之，第1类附加效应最简单。因为在求解附加效应中应先难后易，从第3类附加效应入手，将其消除后再消除第2类附加效应，最后消除第1类附加效应。采用这种“先难后易”的方法的原因是，如果最难解决的第3类附加效应无解，即使能得到系统中其他附加效应的解，系统的复杂性可能依然存在。

系统的附加效应求解过程如图7所示。首先将系统的复杂性转化为附加效应，然后根据4类附加效应的定义顺序求解系统中可能存在的4类附加效应，若无解则应用CAIs软件获取新效应将其替代。待全部求解工作完成后，判断系统中是否产生了新的附加效应，若存在则重复上述步骤，否则求解过程结束。

本文在效应定义的基础上，给出了理想效应和附加效应的定义，并对附加效应进行了分类，为应用附加效应来表达复杂机电系统非线性、开放性、时变特性和耦合性奠定了基础。

3 基于附加效应的设计过程复杂性分析原理及模型

3.1 设计过程复杂性与附加效应

功能需求实现的程度决定了系统DDC的大小，附加效应直接影响系统功能需求实现概率，因此可以应用附加效应表征系统的DDC。DDC理论中用公式的形式描述功能需求和设计参数之间的关系:

(3)

即{FR}=A×{DP}。式中：{FR}为功能需求，{DP}为设计参数，A为设计矩阵。功能需求实现与否只与系统内的设计参数{DP}和相应的设计矩阵A有关，当A为对角阵或三角阵时，功能需求可以实现，当A为一般阵时功能之间的耦合导致功能需求无法满足。设计矩阵中只体现了功能需求与系统内设计参数之间的关系，没有体现复杂机电系统的开放性。

从对附加效应的分类不难看出，附加效应可以来自系统内部也可以来自超系统，但是式(3)只能表达来自系统内部的附加效应。

复杂机电系统为开放系统，超系统的影响是导致系统存在DDC的重要因素。DDC理论将物理过程、设计参数和噪音等归结为可能产生时间相关复杂性的原因。其中：物理过程可能来自系统内部也可能来自超系统，设计参数可能来自系统内部，噪声可能来自超系统。因此可用{DP1,…,DPm}T，{DPa1,…,DPas}T分别表示来自系统和超系统的设计参数，这两组参数共同影响功能需求实现，可描述为

(4)

即{F}=As×{DPs}。式中：{F}为系统功能集合；As为广义设计矩阵；{DPs}为来自系统和超系统的技术参数。

当且仅当

{DPa1…DPas}T→{0…0}T时，{F}={FR}。

将广义设计矩阵中的aij，用对应的输入流xij表示，可以建立理想效应、附加效应与功能需求的关系：

(5)

即{F}=Xs×{Es}。式中：{Es}为理想效应与附加效应的集合；Xs为理想效应与附加效应的输入流集；m为理想效应的个数；n为附加效应的个数。

当且仅当

{Ea1…Ean}T→{0…0}T

时，系统中不存在附加效应，式(5)可以表示为

(6)

即{FR}=X×{E}。

经过上述变换，系统存在的DDC对应的效应关系可以表示为

{Es}=Xs-1×As×{DPs}。

系统中功能Fi与效应之间的关系可以表示为

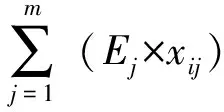
通过将DDC理论中的设计矩阵转化为广义设计矩阵，将系统的功能需求用理想效应表达，系统的DDC用附加效应表达，经典的设计矩阵能够表达系统中功能的关系，但是无法体现复杂机电系统的开放性，通过定义附加效应，可以将超系统对复杂机电系统的影响体现于广义设计矩阵。

通过上述公式表达可以看出，消除系统的复杂性就是要消除附加效应链的影响，可以将系统中的DDC转化为相应的附加效应，通过减小附加效应对理想效应的影响来减小系统的复杂性和信息含量。

3.2 基于附加效应的设计过程复杂性分析原理

理想效应决定了理想情况下系统的功能输出，附加效应与理想效应共同决定了实际状况下系统的功能输出。系统理想效应的输出与效应总输出之比可以表示系统功能需求的实现概率。

基于效应的第i个功能需求的信息含量可表示为

(7)

系统总信息含量可表示为

(8)

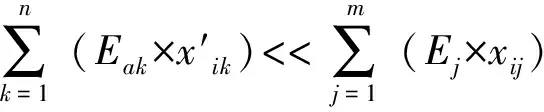
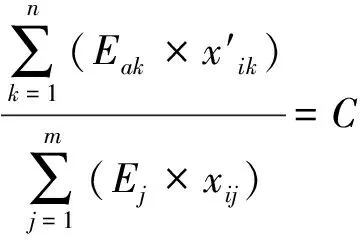
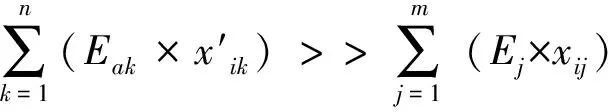
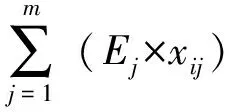
3.3 基于附加效应的设计过程复杂性分析过程模型

通过建立广义设计矩阵表征复杂机电系统非线性、开放性、时变特性和耦合性等重要特征，将广义矩阵中表达的功能与参数之间的关系用效应进行表达，其中用理想效应表达设计者预期的功能，用附加效应表达导致系统出现DDC的功能。

建立基于附加效应的DDC分析模型主要包括以下步骤：

步骤1根据DDC定义确定问题功能。

步骤2用效应表达问题功能及与其相关的功能。

步骤3确定满足功能需求的理想效应和导致系统存在DDC的附加效应。

步骤4应用发明问题解决理论(Theory of Inventive Problem Solving, TRIZ)和计算机辅助创新(Comper Aided Innovation, CAI)软件进行求解，减小附加效应对复杂机电系统的影响。

步骤5评估系统中所含DDC的情况，如果依然存在DDC，则返回步骤2。

4 工程实例

在某纸张厚度测量及检测通路开度调整系统中，采用“电涡流效应”进行纸张厚度检测的方法成本较高，不能满足用户需求，本文应用基于附加效应的DDC分析过程模型分析该系统存在的问题。

步骤1根据设计过程复杂性的定义确定问题功能。

由于系统成本过高导致“电涡流效应”检测纸厚功能无法满足用户需求，确定“检测纸厚”功能为问题功能，该问题功能与时间无关，按照DDC的分类，该问题导致的DDC属于时间相关真实复杂性。

步骤2用效应表达问题功能及与其相关的功能。

系统中存在的时间无关真实复杂性，是由“检测厚度”功能选用了“电涡流效应”导致，即将系统的问题功能用“电涡流”效应表示。

步骤3确定其中满足功能需求的理想效应和导致系统存在DDC的附加效应。

按照附加效应的定义，“电涡流效应”即为导致问题功能的附加效应，系统可以满足功能需求的其他功能为理想效应，这里不再一一分析。

步骤4应用TRIZ和CAI软件进行求解，减小附加效应对复杂机电系统的影响。

为了减小系统的DDC，针对问题功能“检测厚度”应用TRIZ理论中的效应模块进行功能求解，得到可用“超声波效应”和“霍尔效应”替代“电涡流效应”实现该功能。选用液体介质超声波原理进行纸张厚度检测，由于超声波效应构建的系统成本比电涡流系统低，其测量精度和成本均可满足用户需求。

根据上述求解结果得到如图8所示的方案。

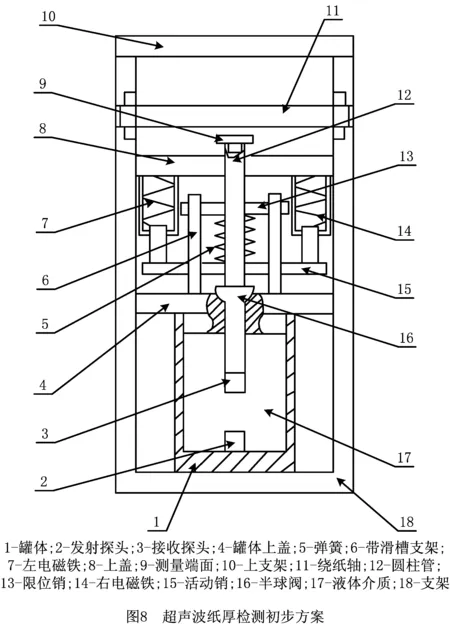
步骤5评估系统的DDC。分析当前系统发现,随着时间的推移，水中溶解空气形成的气泡会在接收探头表面聚集，导致超声波信号传播能量大幅衰减，影响测量结果，使系统范围逐渐移出设计范围，表现为该功能的实现概率逐渐降低，按照DDC的定义和分类，当前系统存在时间相关组合复杂性，需要返回步骤2继续求解。

重复步骤2～步骤5，将超声波信号衰减定义为问题功能，该问题功能对应的效应为超声波效应，即为理想效应。该功能未能完全实现功能需求的原因在于超声波信号传播过程中被气泡衰减，气泡的产生归结于两个效应：①超声波传播过程中产生的“空化效应”导致液体里的气体溢出形成气泡；②在“重力效应”作用下，溢出的气泡在超声波传感器形成空气膜。因此，空化效应和重力效应为附加效应，是导致系统存在时间相关组合复杂性的原因，其中重力效应为超系统对系统的影响。超声波纸厚检测系统理想效应和附加效应的相互影响，如图9所示。

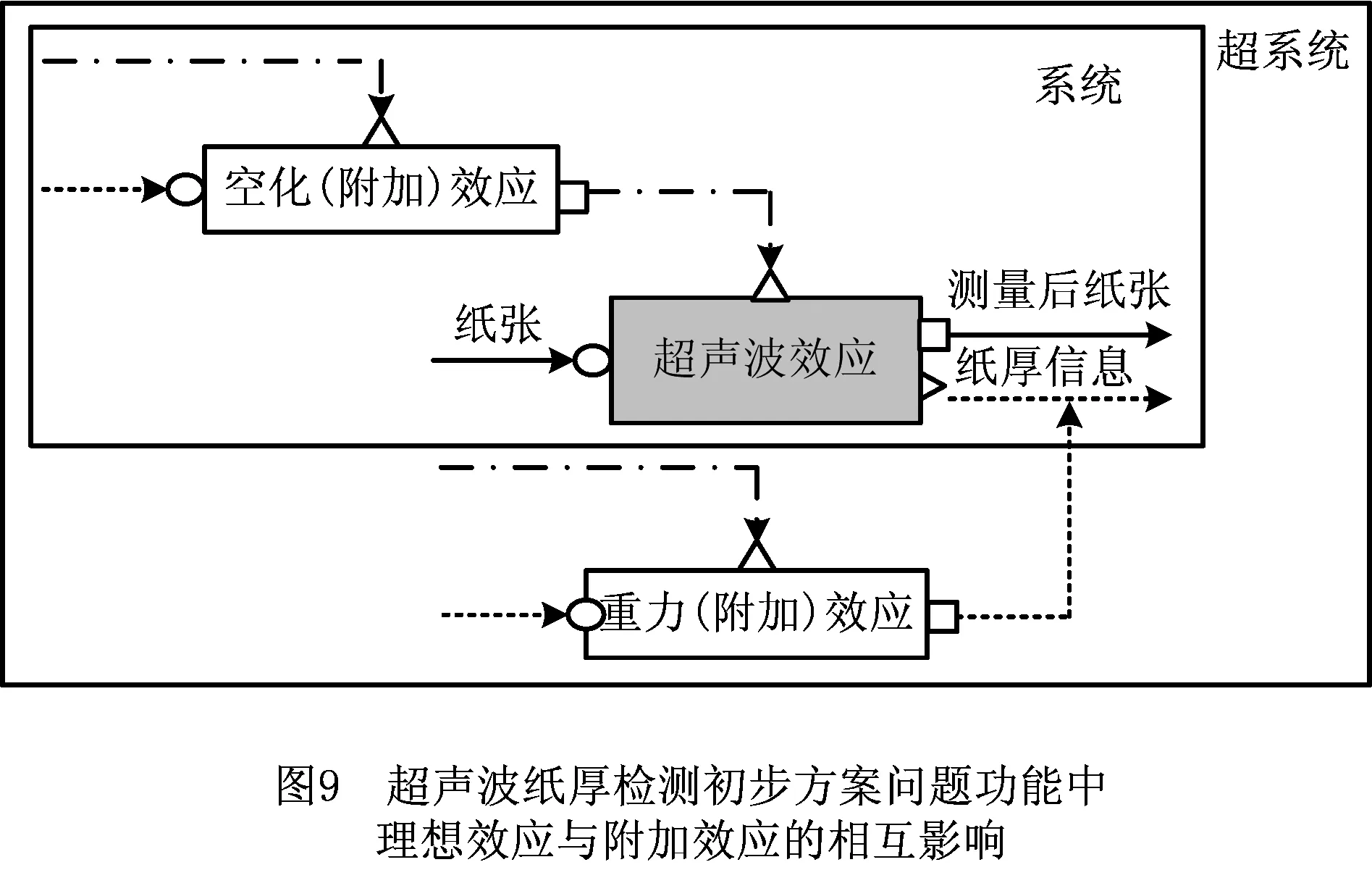
根据式(5)，得到超声波测厚系统的广义设计矩阵

(9)

式中：E1为超声波效应，附加效应Ea1和Ea2分别为空化效应和重力效应。

式(9)可见，Ea1和Ea2对E1产生了影响，要想提高理想效应E1对应的功能实现概率，降低系统DDC，需要降低附加效应Ea1和Ea2对理想效应E1的影响。

选用TRIZ理论中的技术冲突工具对该问题进行求解，系统中的空化效应和重力效应无法消除，但是可以减小其对理想效应的影响。

按照TRIZ理论中技术冲突的定义方法将该问题描述为：为了清除超声波探头表面聚集的气泡，需要增加装置破坏气泡在超声波探头表面的聚集，导致装置更加复杂。应用技术冲突解决理论确定需要改善的参数为“物质或事物的数量”，恶化的参数为“装置的复杂性”，通过查询冲突矩阵确定发明原理为No.3局部质量、No.13反向、No.27用低成本、不耐用的物体代替昂贵耐用的物体、No.10预操作。

根据发明原理13(反向)将整个测厚装置由垂直放置改为横向放置，附加效应中的重力效应虽然还存在，但因超声波探头水平方向，气泡在重力效应作用下向垂直方向聚集，不会造成超声波能量损失，系统中的时间相关组合复杂性减小。

改进后的设计方案将测厚仪横向放置，如图10所示，在罐体上增加了通气管且管口方向朝上，将原来的半球阀换成活塞，改变了原来的支撑方式。改进后的方案消除了气泡的影响，测量值处于误差允许范围内，实现了系统的功能需求。

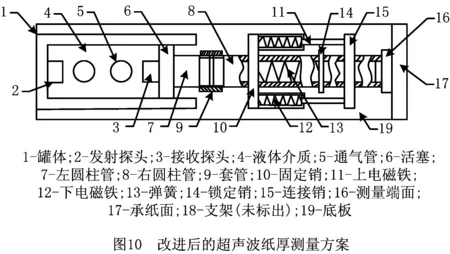
限于篇幅，应用其他TRIZ工具得到的方案，不再赘述。

5 结束语

本文通过用DDC表达复杂机电系统的非线性、开放性、时变特性和耦合性等重要特征，将仅表达系统内耦合关系的设计矩阵扩展为能够表达复杂机电系统特征的广义设计矩阵，并将广义设计矩阵中参数关系转换为附加效应，实现了功能需求—广义设计矩阵—附加效应之间变换，建立了基于附加效应的DDC分析过程模型。该模型以附加效应为分析手段，DDC为特征，将系统中存在的DDC用附加效应表达，可以与TRIZ理论中效应、冲突等工具集成，形成针对复杂机电系统的问题分析和解决工具。本文所提方法在超声波纸厚测量系统设计中得到了验证，也为相关设计提供了参考。

鉴于设计人员从广义设计矩阵提炼附加效应时效率高低不一，未来将以效应库为基础进行相关的转化算法研究，使基于附加效应DDC分析过程模型的使用更加便捷。

[1] LU S C Y, SUH N P. Complexity in design of technical systems[J]. CIRP Annals-Manufacturing Technology, 2009，58(1)：157-160.

[2] SUH N P. Complexity:theory and applications[M]. New York, N.Y.,USA:Oxford University Press, 2005.

[3] LU S C Y, LIU A. Subjectivity and objectivity in design decisions[J]. CIRP Annals-Manufacturing Technology,2011,60(1):161-164

[4] SUH N P. On functional periodicity as the basis for long-term stability of engineered and natural systems and its relationship to physical laws[J]. Research in Engineering Design,2004，15,(1)：72-75.

[5] SUH N P, LEE T. Reduction of complexity of manufacturing systems through the creation of time-dependent periodic complexity from time-dependent combinatorial complexity[J]. CIRP Journal of Manufacturing Systems,2004,33(2):87-100.

[6] MATT D T. Application of Axiomatic Design principles to control complexity dynamics in a mixed-model assembly system:a case analysis[J]. International Journal of Production Research,2012,50(7):1850-1861.

[7] MATT D T. Reducing the structural complexity of growing organizational systems by means of axiomatic designed networks of core competence cells[J]. Journal of Manufacturing Systems,2007,26(3/4):178-187.

[8] ZHANG Peng, YANG Bojun, ZHANG Huangao, et al. Conflict determination direct at CAI based on design-centric complexity[J]. Computer Integrated Manufacturing Systems, 2013,19(2):330-337(in Chinese).[张 鹏,杨伯军,张换高,等.面向CAI设计过程复杂性理论冲突确定原理，计算机集成制造系统，2013，19(2)：330-337.]

[9] ZHANG Peng, TAN Runhua. A study of the rapid acquirement method on ideal result for the complexity of system[J]. Computer Integrated Manufacturing Systems, 2010,16(4):746-754(in Chinese).[张 鹏，檀润华.系统复杂性理想解快速获取方法研究[J].计算机集成制造系统,2010,16(4):746-754.]

[10] SUH N P. Complexity:theory and applications[M]. New York, N.Y.,USA:Oxford University Press, 2005.

[11] TAN Runhua. TRIZ and applications：the process and methods of technological innovation[M]. Beijing:Higher Education Press,2010(in Chinese).[檀润华.TRIZ及应用[M].北京：高等教育出版社,2010.]