基于粒子群算法的CT系统参数标定及优化

宫珊珊，梅立峰，廖志良，黄旭辉

(1.安徽建筑大学 数理学院，安徽 合肥 236001；2.安徽建筑大学 土木工程学院，安徽 合肥 236001)

0 引言

CT(Computed Tomography)，即电子计算机断层扫描，它是利用精确准直的X线束、γ射线、超声波等，与灵敏度极高的探测器一同围绕生物组织或工程材料作连续的断面扫描，具有扫描时间快，图像清晰等特点，可用于多种疾病的检查[1]。

近年来，随着成像技术及后期影像处理技术的发展，CT已在临床疾病检查、筛查、诊断、定位与治疗等方面广泛应用。CT成像原理不仅有助于疾病的诊断和定量分析，而且为疾病数据分析，资料保存提供有效支持。在心血管系统、神经系统、泌尿系统、运动系统、肿瘤定位诊断、靶向治疗、物质分离与鉴别等方面均得到广泛应用，在临床与科研应用中具有广阔的发展空间和应用价值[2]。目前，CT成像系统在系统参数标定以及标定模板的设计方面还存在一定的不足。系统参数的标定和模板的优化，对提高CT系统的精度具有重要的意义。同时，由于CT系统是由各部件组成的复杂系统，系统级的优化并不是系统中局部优化的简单叠加，需要对整个系统的性能进行全局优化。而成像系统虚拟试验技术作为一种应用于射线成像系统设计过程中的高新技术手段，是将来解决这类问题的发展方向[3]。

本文采用2017年全国大学生数学建模竞赛A题中提供的数据(模板的几何信息、吸收强度、未知介质的接收信息均在题目附件中给出)，建立相应的数学模型计算了CT系统模板的参数，并利用这些标定参数对数据进行分析，求解未知介质的相关信息，最后分析了旧模板参数标定的精度和稳定性，并设计和优化了新的模板。

1 模板参数标定计算模型

附件一中已知模板各点吸收率均为1，因此附件二中接收信息值的大小仅于射线穿过介质的长度有关。于是可确定射线与椭圆模板长轴平行时数据出现最大值，射线与椭圆模板短轴平行时数据出现非零值最多。对数据搜索得到射线与椭圆模板长轴平行时是第151列，长轴出现位置在第r1行，射线与椭圆模板短轴平行时是62列，短轴出现位置在第r2行。

由此得到穿过长轴的单位射线数量n1=299、穿过短轴的单位射线数量n2=108、穿过圆形模板直径的单位射线数量n3=29，模板已知信息如图1所示，椭圆长轴长s1=80、短轴长s2=30、圆直径长s3=8，解出探测器单元之间的距离:

探测器单元均匀排列，因此整个发射-接收系统对称分布，而旋转中心即为任意两位置中线的交点。射线平行于长轴时解得旋转中心在直线x=-上，射线行于短轴时解得旋转中心在直线d=6.7820上，因此旋转中心R的位置为(-9.2734,6.7820)。

图1 模板的几何信息

根据CT系统做匀速运动的特点，从射线与椭圆模板长轴平行时到射线与椭圆模板短轴平行时共转过90°[4]，此过程一共进行了89次成像，因此X射线的180个方向两两之间的间隔为1.0112∘，初始位置与水平线夹角为-61.8450∘，转动次数与角度关系式:

2 Radon变换未知介质模型

针对附件二中模板的接受信息进行Radon变换，由于直接变换可能会引起数据损失从而影响成像的准确性，于是对原始数据进行保护处理，即在原矩阵上方和下方加入100×180的零矩阵[5]。输出图像后由于图像范围过大，于是截取载物台范围的像素图，如图2所示。

图2 Radon变换后输出的模板像素图

将得到的像素值生成三维图像，如图3所示，左侧为由附件一数据的生成图形，右侧为对附件二数据进行Radon变换后的生成图形，数据在水平面上较集中且其他颜色的误差干扰较小，从图形的完整性和边缘的连续性看两者差异较小，因此Radon变换可信度较高[6]。

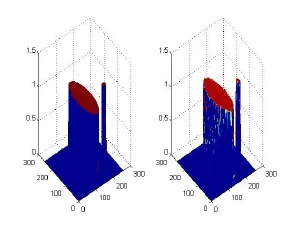
图3 三维建模比较图

将附件一中的数据定义为256阶方阵A1，通过三次插值算法将像素图转换成256阶方阵B1，方阵A1和B1之间存在某种对应关系即A1=k⋅B1，将k定义为衰减系数，k的大小为矩阵对应项比值的平均数，即

同理，对附件三中未知介质的接受信息进行Radon变换输出并截取图像信息如图4所示。该未知介质的位置和几何形状可在图中直观反映，不同颜色代表不同介质材料。

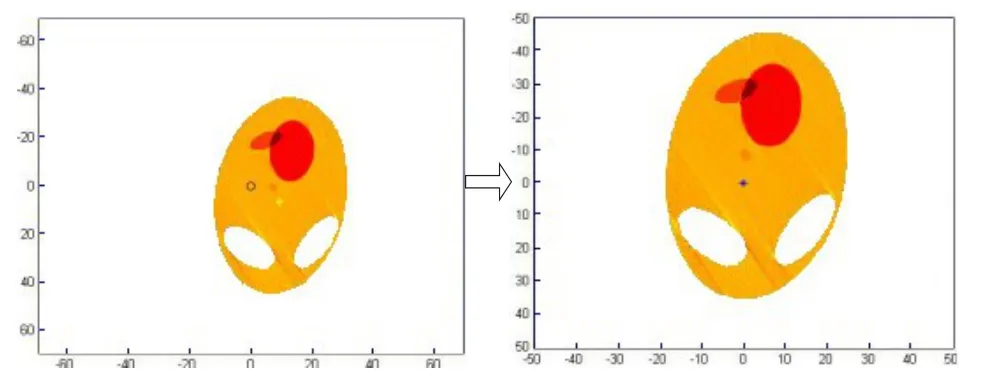
图4 Radon变换后输出的未知介质像素图

通过三次插值算法将像素图转换成256阶方阵B2，利用衰减系数k解得该未知介质的吸收率矩阵A2=k⋅B2，通过代入位置坐标可得到该处的吸收率。

同理，附件五中模板的接受信息进行Radon变换输出并截取图像信息如图5。该未知介质的位置和几何形状可在图中直观反映，蓝色为背景颜色，其余颜色代表不同的材质。

图5 Radon变换后输出的另一未知介质像素图

如图6所示，该介质的边界较为模糊，可能存在数据损失造成成像受损，说明原本的模板或是参数标定精度不高，需要进行优化设计。

通过三次插值算法将像素图转换成256阶方阵B3，利用衰减系数k解得该未知介质的吸收率矩阵A3=k⋅B3，通过代入位置坐标可得到该处的吸收率。

3 PSO参数标定模型

在模板参数标定计算模型中，已经得到一个CT系统的参数，使用该参数，通过rand逆变换可以得到原始图像。但是得到的图像和原始图像有一定偏差(通过图6(b)可以看出图像有所偏移)，原因在于通过模板参数标定计算模型得到的系统参数不够准确，角度的最大偏差可以达到0.5°，探测器之间的距离和旋转中心的最大偏差可随着数据不同而不断改变。因此，在参数的偏差内，一定存在一个最优的参数，得到的图像与原图最为符合。PSO优化算法利用群体中的个体对信息的共享使整个群体的运动在问题求解空间中产生从无序到有序的演化过程，从而获得最优解；利用PSO优化算法，可以使优化后的CT系统的参数更精准，即最佳CT系统参数。

Radon变换生成的像素图与模板图之间的差异越小则参数标定越可靠，即像素矩阵Bi与吸收率矩阵Ai间各项差值综合最小。建立目标函数:

为得到全局最优解，利用粒子群优化(PSO)算法求解。该算法原理简单，容易实现并且没有许多参数的调节。

自变量为旋转中心横、纵坐标、探测器单元距离、X射线的初位置以及每次旋转的角度这五个因素。于是建立五维空间中，其中有N个粒子；粒子i位置:xi=(xi1,xi2,…xi5)，将xi代入目标函数f(xi)求目标值。

设立相关参数，粒子i速度:vi，粒子i个体经历过的最好位置:pbesti，种群所经历过的最好位置:gbesti。

粒子i的第d维速度更新公式:粒子i的第d维位置更新公式:

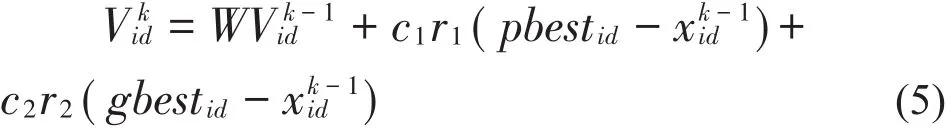
其中vkid是第k次迭代粒子i飞行速度矢量的第d维分量，是第k次迭代粒子i位置矢量的第d维分量；c1,c2为加速度常数，调节学习最大步长；r1,r2为两个随机函数，取值范围[0，1]，以增加搜索随机性；w为惯性权重，非负数，调节对解空间的搜索范围[7]。

利用该算法求解得到，全局最优解在迭代500次时出现。

此时，探测器单元距离为0.2795，旋转中心坐标为(-9.3065，9.7820)，X射线每次的旋转角度为1.0033°，初始位置与水平线的夹角为-61.8043°。此时利用新的参数标定对附件二做Radon变换得到图形与模板原图基本无差别，如图6所示。

此时，精度为1减去差异性函数的最小值，即

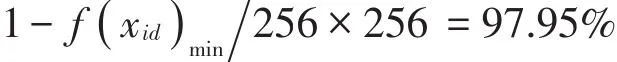
在数据成像过程中，通过牺牲时间，以时间为代价，使每次输出的标定参数更稳定，即成像时间更长怎成像结果更稳定，时间延长为625.2496 s，因此优化后的模型更加稳定。

4 基于PSO的新模板设计

参数标定在计算时由于X射线与模板并不严格相切，且模板较为简单，可取的成像特征较少，所以求解各方向对应角度会存在一定误差，因此精度较差。于是，设计如图7所示的新模板。新模板由八个圆形组成，圆形大小与原模板中圆形大小一致，几何信息如图所示。新模板在成像过程中通过旋转可以找到更多的特殊位置，以便于得到成像过程中的特征点。

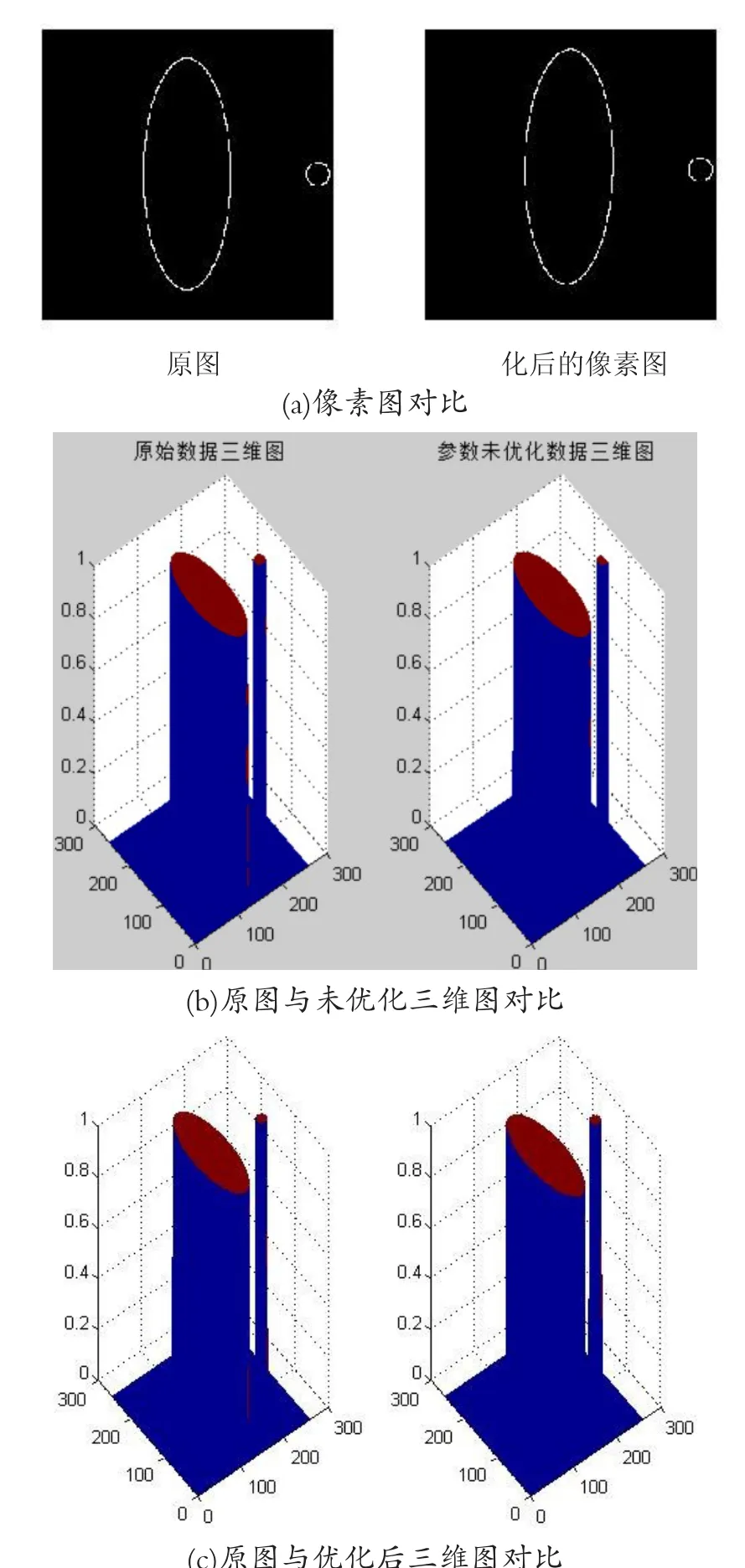
图6 新参数标定下的生成图与模板原图对比

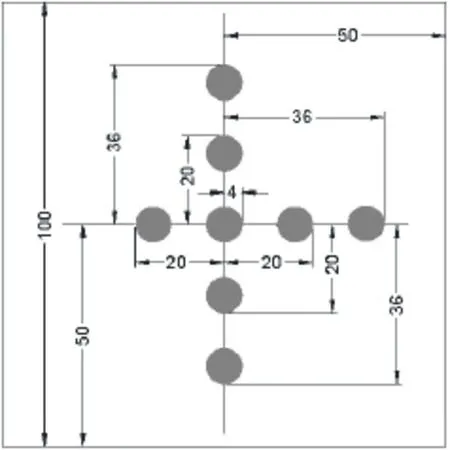
图7 新模板设计图

对比新模板与旧模板采集信息的能力，如图8所示，新模板得到图像的结构更加合理，线条和交点更多，层次更加丰富，因此新模板可采集的数据点更多，信息量更大，从而更有可能找到精确的参数。

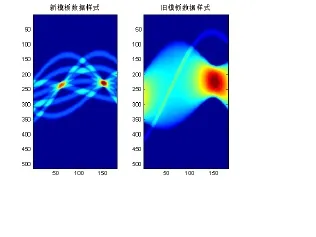
图8 新旧模板数据采集能力对比

将探测器接受信息代入新模板可得到对应的参数标定，利用PSO参数标定模型对参数进行优化，可得到新的标定参数[8]。对模板图像进行三维生成，如图9所示，图形完整、边缘连续、图案较为集中且其他颜色的“噪音”干扰较小，模板较为科学。

图9 新模板三维图像

5 结束语

本文在CT系统的实际工程结构上做了合理简化，建立起既符合实际又便于计算求解的数学模型。利用简单但有效的几何关系求解出模板的参数标定，利用经典的Radon变换求解未知介质的几何信息和吸收率。特别引入粒子群优化算法精确高效的分析了模板的精度和稳定性，并设计新模板以解决旧模板采集数据少精度差的缺点。在此过程中，为方便研究，本文做出合理假设使问题处于理想化的状态，会带来一定的误差，且实际工程中存在一些干扰和噪声等因素，需要结合实际情况另行讨论。