基于分形理论的表面曝气设备故障诊断研究

2018-03-19陈立爱陈松周文忠龚雪何平

安徽建筑大学学报 2018年6期

陈立爱，陈松，周文忠，龚雪，何平

(1.安徽建筑大学机械与电气工程学院，安徽合肥230601；2.安徽国祯环保节能科技股份有限公司，安徽合肥 230061)

0 引言

倒伞曝气机作为常见的表面曝气设备[1-2]，是活性污泥法污水处理达标排放的重要保障[3]。目前曝气设备的运行维护主要采取定期检修和事后维修的方式进行，定期维修由于人为规定检修周期缺乏科学性，可能造成过剩维修或维修不足，有时反而不利于设备的优化运行。同时，复杂设备采用事后维修方式容易带来较大的经济、财产损失。因此，应从“视情维修”的角度对曝气机进行故障诊断。

曝气设备作为一种典型的旋转机械，其运行中振动信号动力学特性呈复杂性、非线性和非平稳性，常规的二值逻辑阈值法很难有效的从振动信号中提取特征信息。分形理论对非线性和非平稳信号具有良好的分析能力，将分形理论引入故障诊断中探讨设备的非线性特征提取方法，实现对机械设备运动状态和定量变化规律行为特征的提取，成为近年来学术界研究的新动向[4-6]。Ghosh[7]通过对机械设备的齿轮磨损状态监测，基于单重分形对齿轮磨损故障的机理进行了研究，取得了很好的效果。

Loutridis[8]等对机械振动信号的时间序列进行了研究，发现振动信号都具有非常明显的自相似特性，利用该特性提出了一种用于早期故障诊断和损伤程度估计的方法，并将其成功的应用于齿轮的疲劳断裂检测中。李萌等[9]从分形原理出发，将其应用于滚动轴承振动信号的定量描述中，研究结果表明分形盒维数能够准确的识别滚动轴承的运行状态。Prieto[10]、Xiao[11]、郝研[12]、董安[13]等也对设备的分形特征进行了研究。分形理论的应用方式、信号分形的演化特征、设备状态的分形维数区间等因设备不同而不同，因此应结合设备特点来研究设备的分形故障诊断方法。

迄今为止以曝气机为对象的故障诊断还未见报道，本文基于曝气机振动信号监测，探讨故障发生时曝气设备振动信号的分形演化特征，为污水处理厂关键设备的物联网技术发展和稳定高效运行提供理论支持。

1 曝气机数据采集

1.1 曝气机构成

倒伞型曝气机主要由电机、减速箱、联轴器、升降装置、倒伞叶轮、电控系统等部分组成，因电机安装方式的不同分成立式型和卧式型，其中立式曝气机因占地面积小、不易受飞溅水花的影响、有效减少因偏心所致的振动和噪音等原因应用较广，为具有代表性本研究以立式曝气机为研究对象，典型的立式曝气机如图1所示。

曝气机在工作时，电动机通过联轴器带动减速箱中的圆柱斜齿轮转动，减速机带动叶轮在污水中低速旋转，叶轮由下而上呈锥形扩张，一方面污水在叶轮的旋转推进作用下，从叶轮的边缘甩出，形成大量水幕并融合大量空气落下，实现污水充氧的效果，同时使得污水上下翻滚充分混合。此外叶轮具有强大的动力带动水流的流动，实现推流效果。

图1 立式倒伞曝气机结构图

1.2 实验仪器及方法

为有效的对曝气机关键部位进行振动信号监测，同时便于历史数据的纵向、横向分析，开发了振动监测仪。该系统由采集设备和软件组成，系统硬件方面包括数据采集卡、振动信号磁性测量探头、USB数据传输装置、计算机。数据采集卡使用并口EPP高速数据交换模式，333.3 K高速采样，14位数模转换器，采集卡中具有1个独立转速通道，通过其完成转速计数与外部触发。外部振动测量探头最大可进行8通道振动数据独立采集和并行处理，并实现同步采样保持，为曝气机不同部位振动信号的多通道、同步并行采样奠定基础。此外，为便于历史数据的保存，设置每次采集的起始点由转速键相信号决定，实现每次采集数据具有相同的相位基准。因在含噪声情况下，测量精度依赖于采样频率的设置，考虑到曝气机电机的工作频率可能随时间变化，系统采用低通滤除高频噪声的同时，可以设置1024/512/256的初始采样频率。

软件部分基于Lab View编制，可以根据不同情况设置采集通道个数，并进行相关参数的设置，包括分析频率、采样点数、通道设置、采集数据类型等等，设置完成后即可进行曝气机振动信号采集。软件可完成振动幅值、有效值、平均值等部分有量纲量的采集和部分无量参数的提取，为后续曝气机故障诊断及故障预警提供有效数据。振动检测仪系统结构图如图2所示。

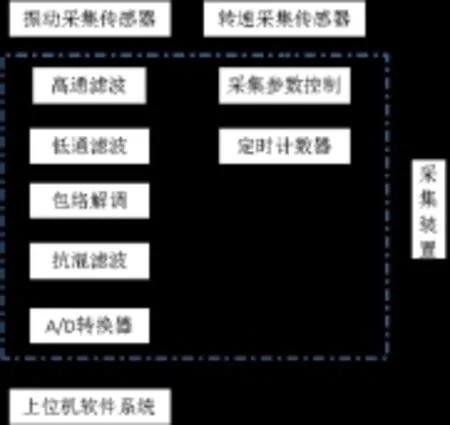
图2 振动检测仪系统结构图

1.3 设备测点选择及参数设置

曝气机故障可能出现在其构成的任何部分，通过对污水处理厂运行维修报表统计发现主要故障源集中在电机、减速机、叶轮处，因此故障诊断测点主要布置在上述三处，以便对其运行状态进行监测，从而能在故障早期发现征兆进行“视情维修”。若监测其它部分运行状态，只要改变测点位置即可。倒伞曝气机测点布置示意图如图3所示。

图3 测点布置示意图

在含有噪声的情况下，振动信号采集的准确性及故障特征提取的计算精度与采样频率直接相关。为保证测量精度，结合曝气机电机及减速箱处的工作频率，实现既能有效监测故障频率的高频成分，同时避免发生频率混叠现象的目的，设置系统的采样频率为1 KHz。采集中采用抗混滤波方式，有效去除低频噪音。

2 分形网格维数故障诊断

2.1 分形理论

分形理论是非线性学科中的一个数学分支，由Maragos P[14]、Chaudhuri B B[15]等首次尝试将其引入到故障诊断领域。在实际工程中，通过对振动信号的波形在一定时域长度下的自相似性进行分析，得出设备不同运行状态下的不规则度。分形故障诊断的最大优点是可以在定性判断故障类型的同时，还可以定量的度量设备故障状态，提高设备故障的识别和诊断能力。单重分形设备故障诊断的主要特征量是分形维数，它可以从整体结构上反映时间序列信号的不规则性和自相似性，定量刻画不同状态下设备信号的分形特征。

2.2 分形网格维数的定义及计算

2.2.1 网格维数的定义

在故障诊断中，实际测得的原始状态信号一般是单变量的时间序列X，设采样间隔为△τ，采样所得的振动信号序列为x1,x2,x3……xn，其中n为原始时间序列采样点数，则有X=Δτ×n。对于不同的时间序列信号，采用不同的△τ进行信号采样，其分形网格维数D定义为:

D反映了设备振动信号的分形特征，不同运行状态下的曝气机振动信号对应不同的网格维数值。

2.2.2 网格维数的计算

将欧式空间Rn分成尽可能细小的边长为Δ的正方体网格时，将集合N离散为数字点集，用NΔ表示离散空间上集合X的计点数。将Δ网格放大为mΔ时，此时用NmΔ表示离散空间上的集合X的计点数，得到K个不同网格宽度上的计点数NkΔ，k=1,2,……。设xk=ln(k)，yk=ln(Nk△)，数据点集(xk,yk)构成的直线斜率则为网格维数。

分形网格维数通常采用最小二乘法进行计算[16]，设直线方程如式(2)所示:

其中，分形维数D作为上述直线方程的斜率，b为截距。

当测定(xk,yk)之后建立目标函数:

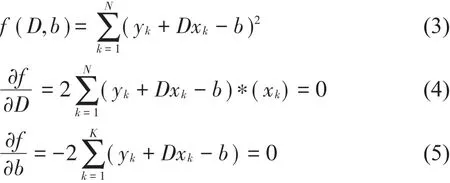
通过对上述函数求解，则可得到网格维数

若对待测状态信号以不同的△ti或采样点数进行采样，根据式(7)计算待测网格维数与已知运行状态的距离，即可实现待检测信号与已知运行模式的接近程度。

式(7)中，Rj,k代表第k种待检测信号与第j种运行模式的接近程度。Rj,k越大时，表明第k种待检测信号与第j种模式越相离。反之，Rj,k越小，表明第k种待检测信号与第j种模式越接近。对于曝气设备通过对运行良好模式和其它运行工况设备的监测，即可判定其它设备的运行模式。若同时对数台曝气机进行振动信号的监测，将其中一台刚过磨合期且运行工况良好的曝气机作为已知信号状态，求得其它运行工况与该曝气机的维数距离，即可完成曝气机运行工况与良好工况的判别。

2.2.3 网格维数距离函数仿真效果分析

式(8)中，待检测信号m1、m2与原始信号y的相位相同、幅值不同，待检测信号y1、y2与原始信号y的幅值和相位均不同。根据2.2.2所示的分形网格维数的计算方法，编制程序计算不同采样周期情况下五组信号的分形维数值，分别以 D、Dm1、Dm2、Dy1、Dy2表示，见表 1。

(1)不同幅值、相同相位信号分形网格维数分析

由表1中不同采样间隔下y、m1、m2的网格维数值可见，随着采样间隔由0.0001变化到0.4096，信号y的网格维数由1.156变化到1.497，信号m1的网格维数由1.158变化到1.853，同时信号m2的网格维数由1.162变化到1.881。总体来说，随着采样间隔的逐步增加，同一信号的网格维数并不是一个固定的值，而是随之逐渐增加。

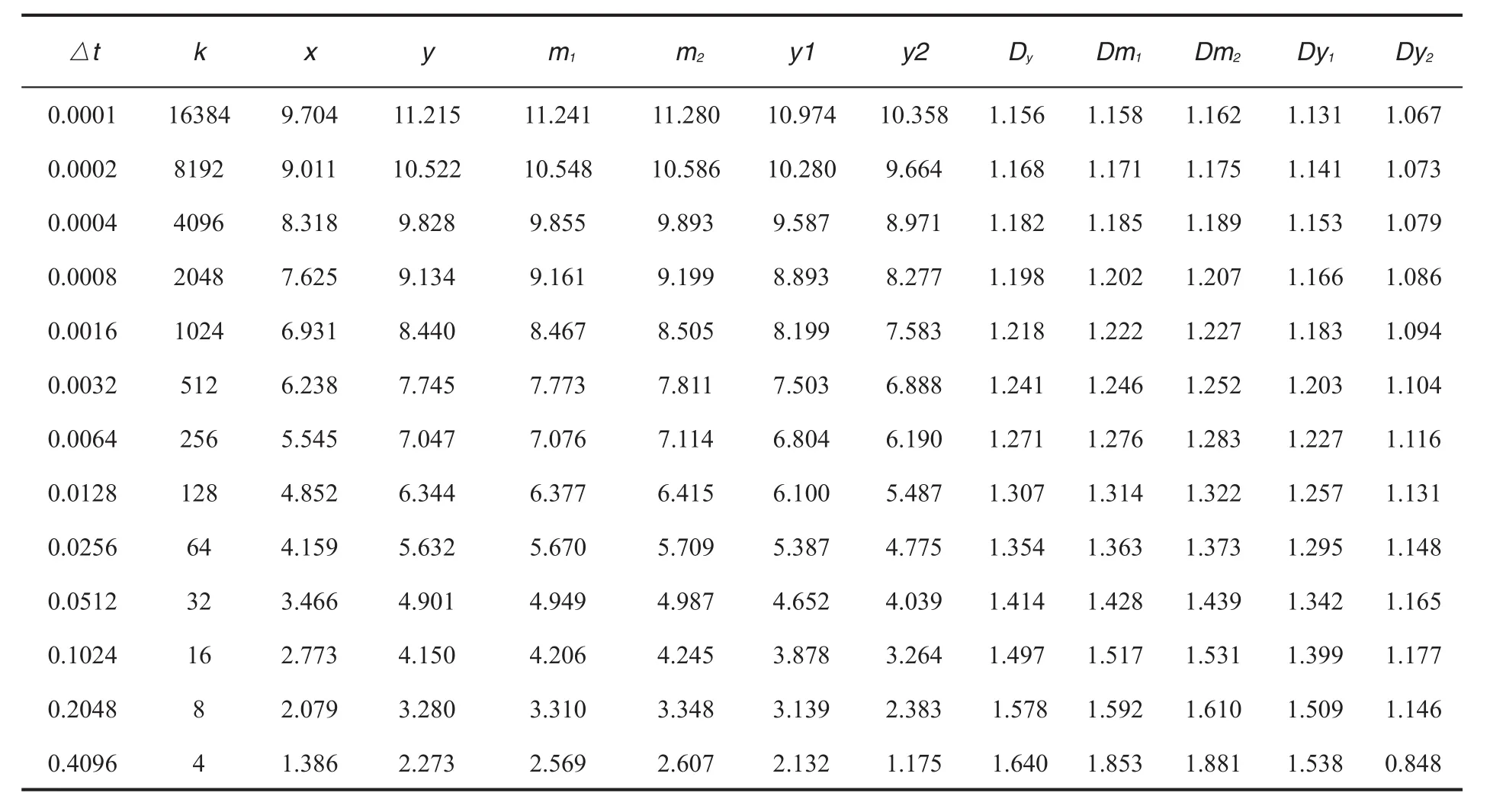
表1 不同采样周期的分形维数值

在采样间隔△t为 0.001 时，y、m1、m2的幅值分别为 1.5、1.54、1.6，其网格维数分别为 1.156、1.158、1.162，既在相同的采样间隔情况下，幅度越大，分形维数值越大，其它采样间隔情况下同样满足该特征。

为便于直观比较m1、m2两个待检信号与原始信号直接的接近程度，以采样间隔△t为横坐标，信号y、m1、m2的维数值为纵坐标绘制图形，如图4所示。

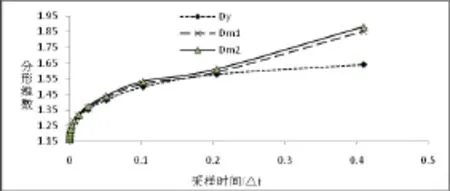
图4 模拟信号分形维数分析

根据式(7)计算信号状态m1、m2与状态y的分形维数距离，如表2所示。

表2 维数距离值

由表2可见，m1与y的维数距离小于m2与y的维数距离，说明m1比m2更接近于y。而实际上y的幅值为1.5，m1的幅值为1.54，m2的幅值为1.6，同样从图4中也可以得到相同的结果。即相位不变、幅值逐步增大时，分形维数距离也会逐步增加，反之亦然。

(2)不同幅值、不同相位信号分形网格维数分析

在信号幅值和相位均不相同的情况下，随着采样间隔由0.0001变化到0.1024，信号y的网格维数由1.156变化到1.497，信号y1的网格维数由1.131变化到1.399，同时信号y2的网格维数由1.067变化到1.777。总体来说，对于同一信号满足幅值越大、分形维数值越大的特征。但是当采样间隔增加到一定程度(t=0.4096时)，出现网格维数减小的情况，这主要是由于采样间隔过大使得采样后信号失真造成的。

同样为便于直观比较上述y1、y2与y的接近程度，以采样间隔△t为横坐标，信号 y、y1、y2的维数值为纵坐标绘制图形，如图5所示。

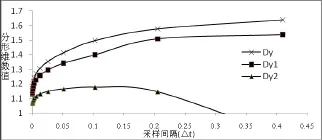
图5 模拟状态下的分形维数图

表3 y1、y2与y的维数距离

计算信号状态y1和y2与y的维数距离，如表3所示。

由表3可见，y1与y的维数距离小于y2与y的维数距离，说明y1比y2更接近于y，从图3中也可以得到相同的结果。因此，分形维数距离公式可以判定待检信号状态与已知信号状态的关系。

3 曝气机故障诊断

3.1 数据采集结果

为减少测量误差在监测中采用定人员、定时间、定测点参数、定测点部位、定测量仪器的“五定”作业制度，对合肥市经开区某污水处理厂实际运行的倒伞型表面曝气机进行了的振动监测，为便于表述设曝气机为G。考虑到设备故障信号具有延时和渐变的特性，选取某年中2月、5月、7月、10月和12月的测量数据进行分析，分别以序号1-5代替。由振动监测仪采集的曝气机G的时域和频域波形图如图6和图7所示。

图6、图7中，自上而下、自左而右为曝气设备G测点1至测点6的时域波形图。通过对时域和频域波形图的定性分析可见，测点1与测点6、测点3与测点4、测点5与测点6的时域信号图和频域波形图具有相似的变化特征和较为接近的信号幅值。这是由于振动测试仪器探头为单轴型位移传感器，测量时每个探头只能对单方向振动信号进行监测，为全面获得测点信息振动信号探头成套配对使用，上述三对测点分别反映电机输入、输出端和减速箱输出端径向、轴向的振动特性，因此其信号波形图较为相似，后续分析只对测点1、测点3、测点5进行。三组测点中，测点1、2处振动幅值最大，最大处达到1.8 mm，其运行状态最差，测点5、6处次之，测点3、4处的振动幅值最小。

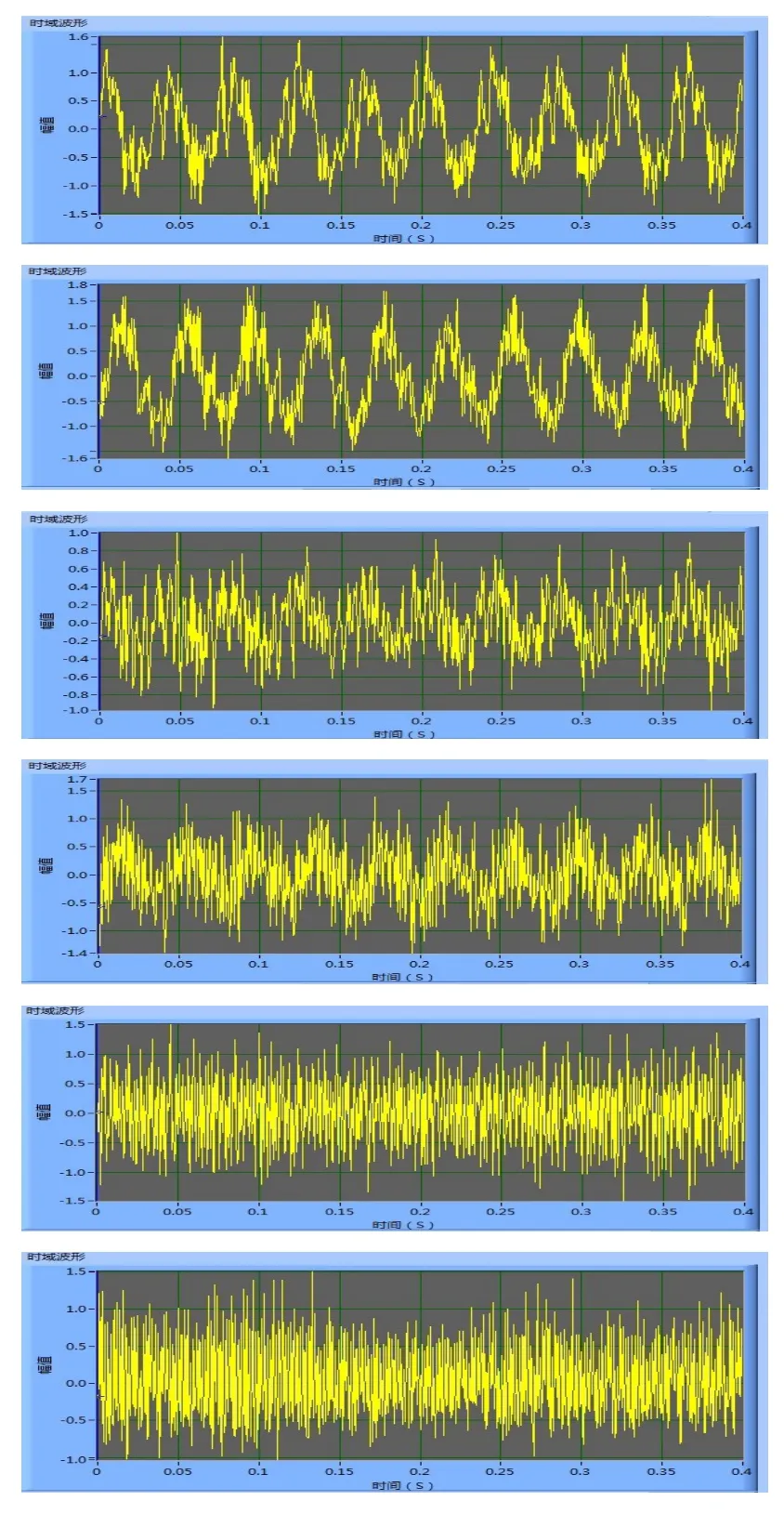
图6 测点时域波形图

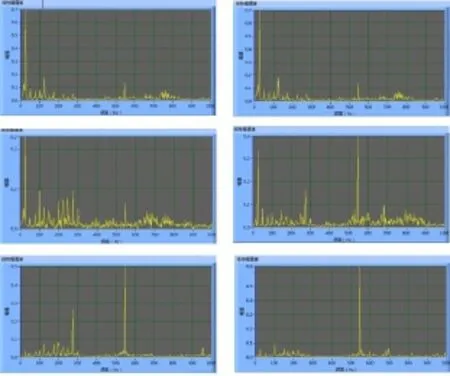
图7 测点的频谱图

3.2 基于分形网格维数的数据分析

3.2.1 网格维数与采样点数的关系

在采样频率为1 KHz的情况下，采样时间长度0.4 s，分别以采样点数为1024和512对系统进行采样，对设备G进行数据采集并进行了抗混滤波处理后，分别计算3个部位测点的维数特征，结果如图8所示。

图8 不同采样点数的网格维数特征

由图8可见，在能有效采集曝气机振动信号的情况下，网格维数值不仅与采样频率有关[13]，而且同样受到采样点数的影响。在相同的采样时间内，当采样点数减少时，测点一、测点三、测点五的网格维数均存在不同程度的增加，说明网格维数与采样点数呈反比关系，这与采样时间、系统分维数随采样频率变化的趋势相同。在采样时间确定的情况下，当只改变采样点数而其它条件保持不变时，若采样点数变小，则曝气机时间序列信号的分形维数值变大。反之，当采样点数变大时，分形维数值变小。因此对曝气机进行故障诊断确定不同运行模式的分维区间时，必须在相同的采样设置情况下才有意义。

3.2.2 网格维数随时间的变化

对图6中的时域图形进行整周期数据提取，分别对每一测量时间内的测点按网格维数计算方法计算测点处的分形维数，其网格维数变化趋势如图9所示。

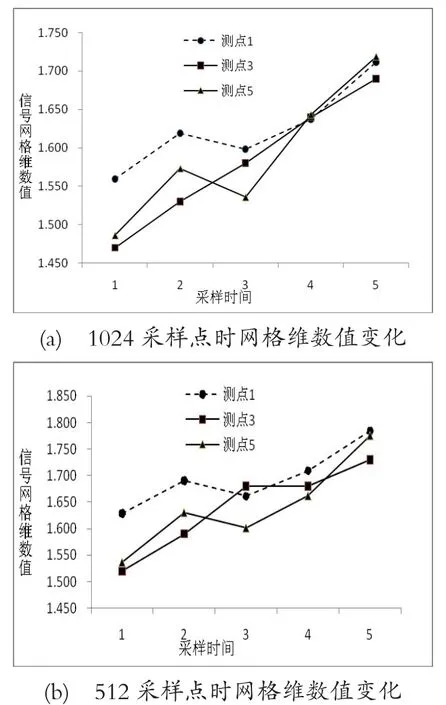
图9 网格维数随曝气机运行时间的变化趋势

由图9可见，因测量时间的不同，曝气机的运行模式不同，三个测点的分形维数均发生改变，最大的维数值达到1.72，最小维数值为1.43。网格维数值随着曝气机运行时间的延长有逐渐升高趋势，这与模拟状态下的信号网格维数的变化趋势相同。此外，由于因信号自振动源产生后振动传递系统的不同，或在传递过程中受齿轮箱、联轴器等第二信号源的影响，造成同一台设备的不同部位表征其运行状态的网格维数值并不相同。因此对曝气机进行故障诊断时，针对容易发生故障的部位都应进行测量，建立相应的数据库档案，以便后续曝气机故障诊断专家库的建立。

3.2.3 同一测点分形维数比较

计算设备G测点一和测点二的分形维数值并画出图形如图10所示。

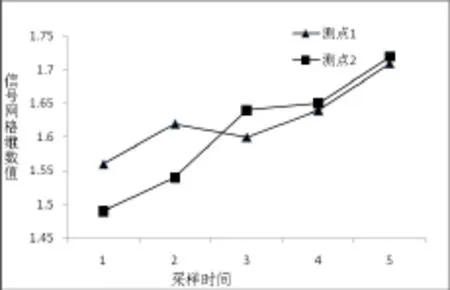
图10 同一部位网格维数对比

同一台机器同一测点处的维数值，因测量部位的不同振动信号有所差别，最终反映运行状态的分形维数并不是一个确切的数值，而是位于一个跳动的区间内，并且区间范围不同，最小差别为0.01，最大为0.08，见图10所示。这是由于倒伞曝气机的测点振动值受多方面的影响，例如污水厂日处理水量不同、排水量不同或回流比不同等等，使倒伞表面曝气机的工作效率受污水液位影响，造成因测量方向不同导致分形维数值可能不相同。但是总体可以看出，各个测点的变化趋势相同，即一个测点维数值随着测量时间的变化规律同样适用于该机器上其它测点维数值的变化规律。

3.2.3 曝气机运行状态故障识别

该厂同一个氧化沟中有相同型号、投入运行时间相同的曝气机4台，共同完成污水的曝气和推流，为对设备进行横向对比，对4台曝气机的振动状态进行了监测，运行模式良好的曝气机M的网格维数值作为已知状态，G、G1、G2作为待检测的运行状态，不同机器测点1、测点2的网格维数值如表4所示。

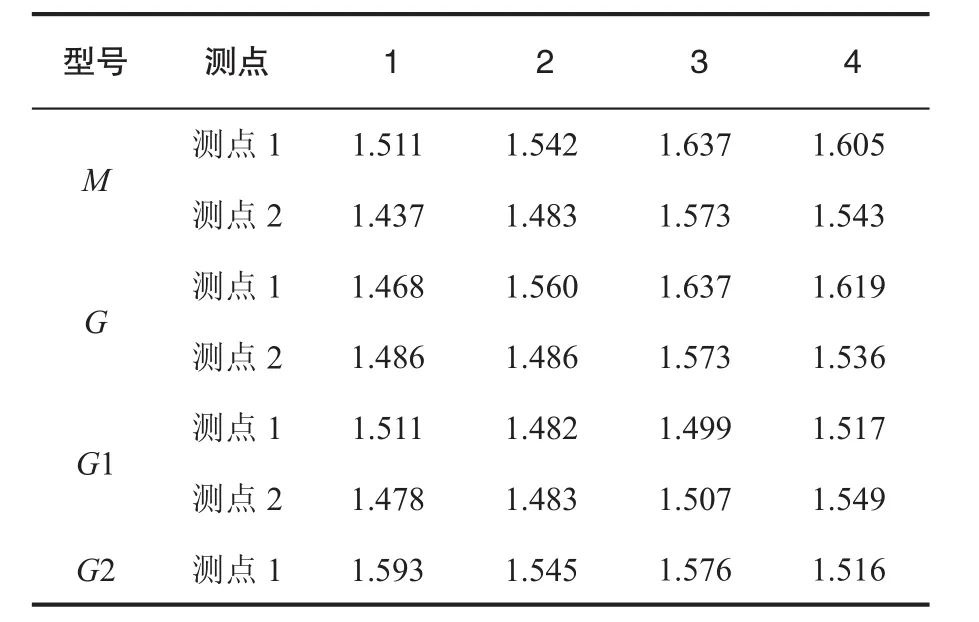
表4 不同机器的测点维数值

测点2 1.488 1.504 1.506 1.643

计算M与G、G1、G2测点1与测点2的分维数距离，见表5所示。

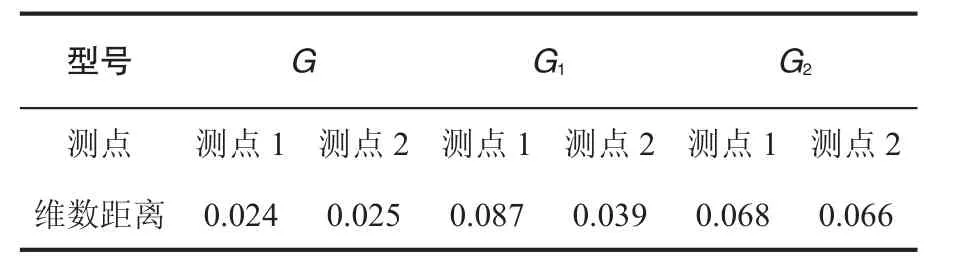
表5 已知模式与待检测模式维数距离

由表5可见，G、G1、G2与已知模式M的网格维数距离因运行模式的不同而不同，其中G测点一和测点二维数距离值均较小，运行模式与M状态最为接近，说明其运行工况相似，运行良好。G1测点二维数值较小，测点一较大，由于测点一和测点二均是曝气机电机主轴上选取的测点，但因测量方向的不同使其维数值存在差别，为便于综合比较对表5测点一、二数据求取几何平均值如表6所示。

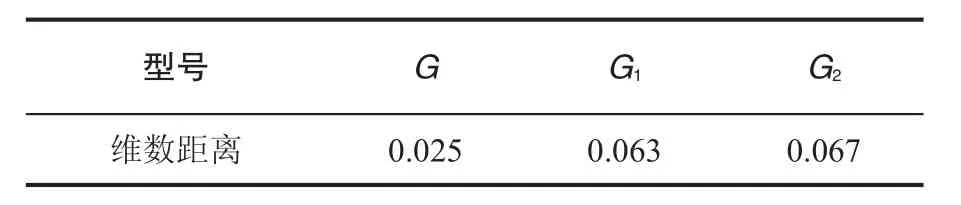
表6 已知模式与待检测模式维数距离几何平均值

从表6可见，设备G的网格维数距离仅为0.025，同样说明其运行状态与M最接近，运行状态最佳。而G1和G2的网格维数达到了0.063和0.067，其运行状态较差，可见网格距离维数可以有效的实现待检测状态与已知状态的有效区分。后期继续运行过程中，要严密监视G1、G2的运行工况，一旦发现其维数值或幅值发生突变，则必须停机检修，否则将带来不可估计的后果。