基于极限承载比的大跨桥梁结构内力监测方案设计
2018-03-19谢政王佐才任伟新胡可
谢政,王佐才,任伟新,胡可
(1.合肥工业大学 土木与水利工程学院,安徽 合肥 230009;2.安徽省交通控股集团有限公司,安徽 合肥 230088)
0 引言
桥梁在长期使用过程中,由于车辆、风、地震、环境因素等作用,以及材料自身性能的不断退化,导致桥梁结构产生不同程度的损伤和劣化。这些损伤如果不能及时得到监测和维修,可能会造成严重的影响,比如导致桥梁破坏和倒塌。为保证桥梁结构的安全性、实用性和耐久性,加强对桥梁健康状况的监测和评估十分必要[1-2]。
结构健康监测起初主要用于航空航天领域,一般被用来获取结构的荷载。但随着结构设计的复杂化、大型化、智能化的发展,结构健康监测也有了进一步的发展,不再仅仅局限于对荷载的监测,结构损伤检测及定位、结构安全状态评估与寿命预测也都成为其研究的内容[3]。1997年,Housner等人[4]将结构健康监测系统定义为:一种从营运状态的结构中获取并处理数据、评估结构主要性能指标(如可靠度、耐久性等)的有效方法。2009年,Boller等人[5]将结构健康监测定义为一种通过一系列传感设备,将无损检测技术嵌入结构和材料的方式对结构荷载、损伤状态进行记录、分析、定位和预测的技术。
美国最先在威斯康星州Michigan Street Bridge上安装了世界上第一套远程监测系统,可以实现对裂缝的发展状况和其他状态参数变化的监测[6]。英国对爱尔兰的Foyle桥在80年代安装了实时监测设备,以研究车辆、风及温度对大桥响应的影响。该系统作为安装较早且较为完整的监测系统之一,可以做到对桥梁状态参数的实时监测、实时分析[7]。我国的李惠和欧进萍教授[8-9]提出了大跨斜拉桥健康监测系统的设计与实现,提出桥梁健康监测系统的总体设计原则,传感器优化布置方法,数据采集与传输系统的设计原则和方法等。
传统的桥梁监测系统,往往监测指标较为全面,监测截面众多,监测数据量巨大,系统庞杂。为了更好的优化桥梁健康监测系统,刘文峰等[10]采用基于应变模态得到的广义应变能密度的结果作为评估参数来确定杭州湾跨海大桥健康监测系统中应变传感器的最优布点。伊廷华等[11-12]对传感器的优化布置做了深入研究,对比研究了简易遗传算法和广义遗传算法的特点,并对广州新电视塔的传感器布置进行了研究,给出了不同的优化布设方案;缪长青[13]等在润扬长江大桥的健康监测中,对大桥的结构设计特点、环境状况、营运工况等进行了分析研究,建立了一个精细的三维有限元模型,通过对理论模型进行静动力分析,确定结构应力集中点、位移值点等关键部位,进而确定了传感器布设的最优方案并开发了大跨度桥梁结构健康监测系统;孙利民等[14-15]在对结构各损伤场景的易损性作定量分析后,提出了一种以监测结构易损场景为目的的传感器布设方法,并阐述了易损性分析在大跨度桥梁结构健康监测中的应用。在国外,Hong等[16]对路网上的混凝土梁桥按装了精简的健康监测系统,主要监测结果的加速度和关键截面的应变。Brownjohn等[17]对英国的部分中小桥梁建立精简的监测系统,主要监测加速度,关键截面应变和位移。Kister[18]则通过开发适当的光学传感器保护系统,仅利用光纤传感器建立了钢筋混凝土柱和梁进的应变监测系统。
但是,目前的桥梁结构内力监测设计还很难考虑结构在不同荷载情况下可能的真实破坏过程。基于桥梁设计极限状态方法确定的是设计荷载水平下的结构应力和变形,但是,桥梁结构在设计时一般采用等强度设计理念,即受力大的构件使用大的截面尺寸,而相对受力小的构件使用小的截面尺寸,因而在桥梁设计极限状态下,构件的承载比往往比较均匀,无法完全确定极端状况下结构的薄弱构件。特别是当荷载水平超过设计荷载水平时,使得结构达到真实破坏状态时,就必须考虑结构的真实极限状态,确定极限承载状态下的结构薄弱部位。
为了定量化确定内力监测构件,论文提出了基于构件极限承载比的结构内力监测设计理论与方法,该方法是通过对不同荷载组合作用下的大跨度桥梁结构的极限承载能力进行分析,找出结构中的高承载构件及破坏路径。通过定义构件极限承载比与基准极限承载比等特征参数,对构件的承载能力状况进行定量分析,从而确定桥梁结构的高承载构件,进而确定监测构件和监测指标。论文最后以芜湖长江公路二桥为工程背景,通过对六种荷载组合作用下的桥梁结构极限承载能力分析,找出其中的高承载构件及破坏路径,进而对芜湖长江公路二桥进行内力监测方案设计。
1 基于构件极限承载比的结构内力监测方案设计理论
1.1 基于极限承载能力的构件极限承载比与基准极限承载比
根据桥梁构件截面内力与相应截面强度之比,可以定义构件承载比、承载比均匀度、基准承载比等参数,定量确定不同荷载作用下结构中各构件承载比特征参数,反映结构承载状态下各构件承载情况与整体分布状态。
构件承载比定义为截面内力与相应截面强度的比值。

式中:re表示构件承载比,其中上标e表示构件编号;Q和Qp分别表示构件e的截面内力和截面强度。
构件承载比均匀度可以定义为:

其中,ˉ为结构中构件承载比的均值。rmax和rmin分别表示各构件承载比中的最大值和最小值。d为分析结构的承载比均匀程度。
构件基准承载比进一步定义为:

每种荷载组合作用下,随着荷载的不断增大,构件承载比和基准承载比也随之改变,当桥梁结构达到极限承载能力时,截面内力与相应截面强度的比值定义为构件极限承载比,对应的基准承载比定义为基准极限承载比。

式中:relim表示构件极限承载比,其中上标e表示构件编号,下标lim表示结构达到极限状态;Qlim和Qp分别表示结构达到极限状态时构件e的截面内力和截面强度。
类似的,极限承载比均匀度的定义为:

式中:rˉlim为结构中构件极限承载比的均值和分别表示结构达到极限状态时各构件承载比中的最大值和最小值。dlim表示所分析结构的构件极限承载比均匀程度,其动态取值范围为(0,1]。
同样,基准极限承载比定义为:
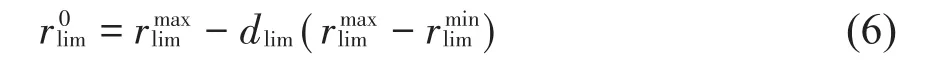
基于特征参数定义的基准极限承载比r0lim提供自适应识别高承载构件的基本准则。凡是构件极限承载比高于基准极限承载比的构件为高承载构件,反之,则为低承载构件。当构件极限承载比等于1时,表明该构件已经发生破坏,破坏构件是特殊的高承载构件。
1.2 基于构件极限承载比的结构内力监测方案设计
基于构件极限承载比的大跨度桥梁结构内力监测方案设计的基本思想是通过对不同荷载组合作用下的大跨度桥梁结构的极限承载能力分析,找出结构中的高承载构件及破坏路径。通过定义构件极限承载比与基准极限承载比等特征参数,对构件的承载能力状况进行定量分析,从而确定桥梁结构的高承载构件,进而确定监测构件和监测指标。
通过对大跨度桥梁结构的不同荷载作用下的极限承载能力分析,研究不同荷载作用下结构最为薄弱的部位。当结构在某种荷载工况下,所受外荷载逐渐增大,造成某个构件的破坏时,它所承担的荷载就会重新分布到相邻的构件上,其相邻的构件又遭到破坏,继续进行内力重分配,直至整个结构破坏,这个过程就是结构的一条破坏路径。破坏路径上构件的极限承载比等于1,属于结构的最为薄弱部位,破坏路径上的构件,也是结构最易发生损伤的构件,也属于结构的薄弱部位,也是结构中的易损构件。因此,在基于桥梁结构极限承载能力分析的内力监测方案设计时,除了对于已破坏的构件进行监测外,对于高承载构件,可列入监测范围。
具体来讲,对于大跨度桥梁结构,对斜拉索这种每一根都是一个单独的构件,应重点监测其已发生破坏的构件;对于主梁和主塔这种具有连续性的构件,应重点监测其首先发生破坏的高承载构件或者构件极限承载比最大的高承载构件。
通过极限承载能力分析找到大跨度桥梁结构中的高承载构件及破坏路径,基于高承载构件及破坏路径进行大跨度桥梁结构内力监测方案设计。
2 芜湖长江公路二桥极限承载力分析
2.1 桥梁概况
芜湖长江公路二桥跨江主桥桥跨布置为(100+308+806+308+100)m,为双塔四索面分离式钢箱梁斜拉桥。斜拉索按照空间扇形布置;主梁为扁平弧形底板分体式钢箱梁,正交异性桥面板,总宽度达53 m;主塔为分肢柱式塔,桥塔总高度为259.48 m。芜湖长江公路二桥的立面图见图1,主梁横断面图见图2。

图1 芜湖长江公路二桥立面图
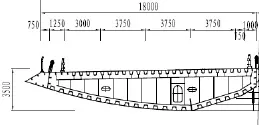
图2 芜湖长江公路二桥主梁标准断面图
2.2 有限元模型
利用有限元软件ANSYS建立芜湖长江公路二桥结构的有限元模型,见图3。其中主塔、主梁和箱型横梁采用空间梁单元BEAM188模拟,边墩、辅助墩采用空间梁单元BEAM4,斜拉索采用空间杆单元LINK180模拟。边界条件为:索塔底部采用完全固结。桥梁结构中,主塔塔身采用C50混凝土;主梁钢箱梁采用Q345钢材;斜拉索采用公称直径15.2 mm钢绞线。桥梁中各种材料参数如表1所示。其中主梁及横梁钢材采用双线性随动强化模型BKIN模拟,其本构关系曲线如图4所示,其中屈服应力σy为345 Mpa,弹性模量E为2.06×105Gpa。斜拉索采用理想弹塑性模型模拟,屈服强度为1860 MPa。主塔混凝土σ0为混凝土抗压强度标准值,C50混凝土为32.4 Mpa;ε0和εu分别取0.002和0.0035,应力-应变曲线关系采用德国学者Rusch提出的应力-应变曲线函数[19],如图5所示,具体表达式为:
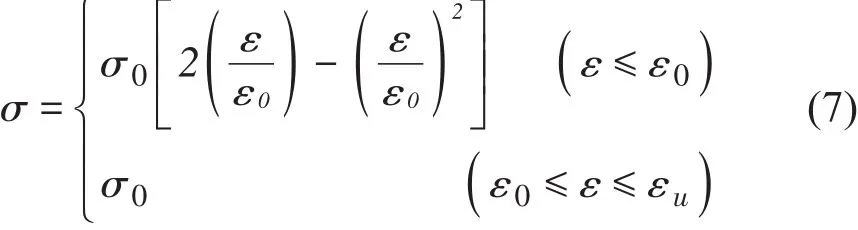
材料非线性分析中的破坏准则采用Von-Mises屈服准则。
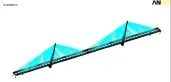
图3 芜湖长江公路二桥有限元模型图
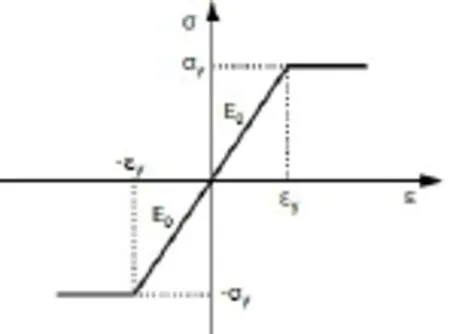
图4 钢材应力—应变关系曲线
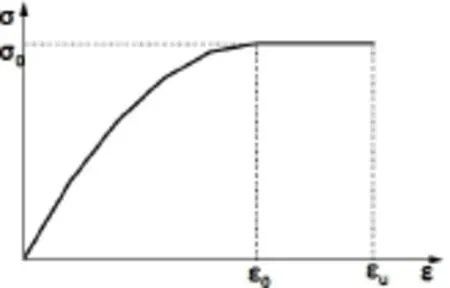
图5混凝土应力—应变关系曲线
2.3 极限承载力分析
考虑了几何非线性及材料非线性结构极限承载能力分析,主要是通过不断增加工作荷载的大小,对桥梁结构进行全过程分析,寻找结构的荷载位移曲线的极值点,当到达极值点后微小的荷载增量都会引起结构变形急剧增加,按极值点失稳理论求得的结构失稳临界荷载值取为结构的极限承载力。
进行极限承载力分析时,设置两个荷载步,第一荷载步施加全部恒载,第二荷载步逐级施加外荷载,直至结构破坏。在考虑几何非线性与材料非线性的同时,对芜湖长江公路二桥进行极限承载力分析时,主要考虑六种工况,见表2,得到六种工况下芜湖长江公路二桥应力的计算结果,见图6至图7,论文中所取的应力为单元截面的主应力。在当结构达到极限承载状态时,工况1至工况6的荷载放大系数 n 分别为 :14.20,8.67,11.65,14.52,50.12,26.24。

表2 荷载工况
2.4 构件极限承载比、极限承载比均匀度、基准极限承载比计算
为了计算构件的极限承载比,把有限元模型中的每一个单元假设为一个构件。把斜拉索构件、主梁构件、主塔构件划分为三组构件,在每一工况下,对每一组构件,进行极限承载比、极限承载比均匀度、基准极限承载比计算,通过基于极限承载能力分析的结果,可获得每一工况下每一组构件中各构件的极限承载状态下所受的应力,再根据公式(4)-(6)可计算出每一工况下每个构件的构件极限承载比、极限承载比均匀度、基准极限承载比。
图6 工况1-工况6主梁应力图

图7 工况1-工况6主塔应力图
以工况2为例,对斜拉索构件、主梁构件、主塔构件三组构件分别进行极限承载比、极限承载比均匀度、基准极限承载比计算。计算出斜拉索构件组的平均构件极限承载比=0.49,最大的斜拉索构件极限承载比为=0.83,最小的斜拉索构件极限承载比为=0.08,进一步计算获得斜拉索构件组极限承载比均匀度dlim=0.43,以及基准极限承载比0.51。同理可计算出:主梁构件组的基准极限承载比=0.73,主塔构件组的基准极限承载比=0.42。在工况2中,各构件的极限承载比如表3所示。在表3中,斜拉索构件组列出了上游幅1/2跨范围内的斜拉索的构件极限承载比,分别是,上游幅外侧斜拉索A1至A25、内侧斜拉索A'2至A'25。主梁构件组列出了上游幅1/2跨范围内的主梁构件的构件极限承载比。主塔构件组列出了Z3主塔构件的构件极限承载比。
基于上述分析可计算出每种工况下斜拉索构件、主梁构件、主塔构件三组构件的基准极限承载比,见表4所示。当构件极限承载比等于1时,表明该构件发生破坏,每种工况下芜湖长江公路二桥的破坏构件及区域,见表4。
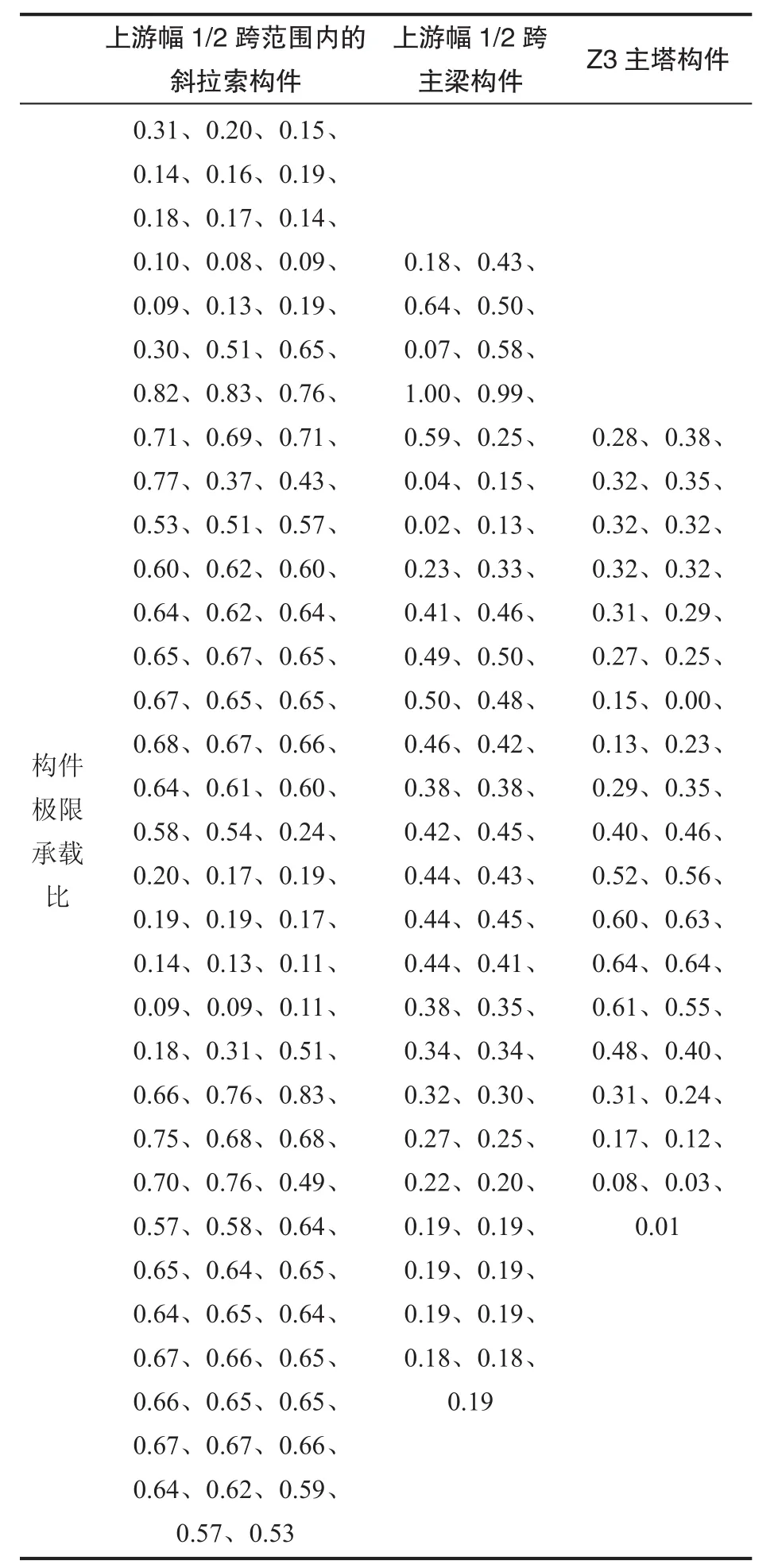
表3 构件极限承载比
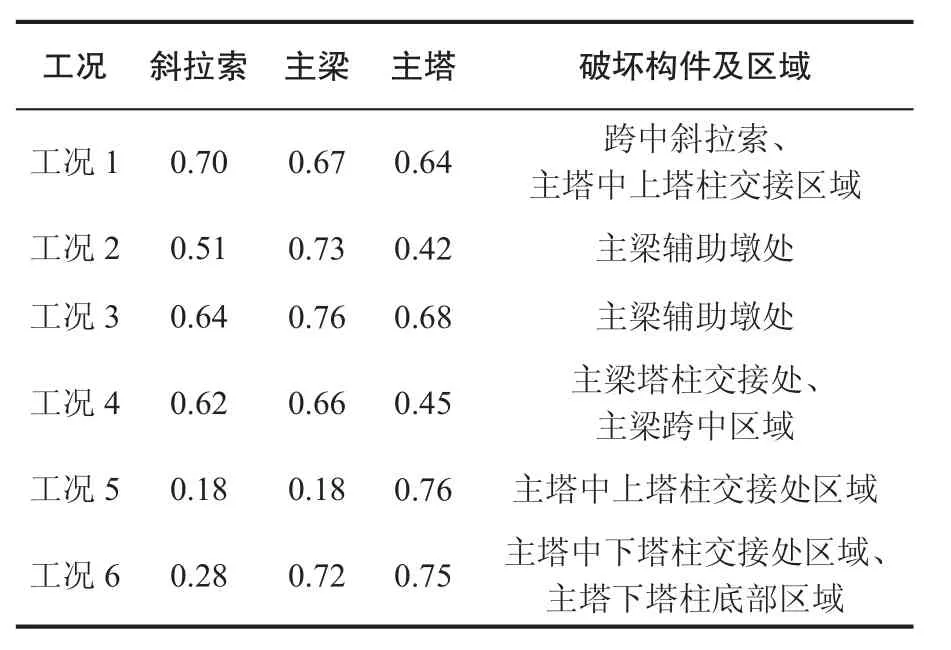
表4 基准极限承载比及破坏构件
3 基于构件极限承载比的芜湖长江公路二桥内力监测方案设计
在芜湖长江公路二桥极限承载能力分析的基础上,结合基于构件极限承载比的桥梁结构内力监测设计理论和方法,给出芜湖长江公路二桥内力监测方案设计。
3.1 斜拉索索力监测
在工况1中,斜拉索高承载构件分布在边墩区域、边跨跨中区域、主跨1/4区域和主跨跨中区域。边墩区域中,外侧索面中斜拉索A25构件极限承载比最大,为0.79;边跨跨中区域中,内侧索面中斜拉索A'10构件极限承载比最大,为0.97;主跨1/4区域中,内侧索面中斜拉索J'12构件极限承载比最大,为0.88;主跨跨中处外侧索面斜拉索J25和内侧索面斜拉索J'25构件极限承载比等于1,该处斜拉索发生破坏。工况2中,斜拉索高承载构件分布在边墩区域、辅助墩区域和主跨1/4区域;边墩区域中,外侧索面中斜拉索A25构件极限承载比最大,为0.77;辅助墩区域中,辅助墩处斜拉索A20和A'20构件极限承载比最大,都为0.83;主跨1/4区域中,内侧索面中斜拉索J'12构件极限承载比最大,为0.67。工况3中,斜拉索高承载构件分布在边跨跨中区域;边跨跨中区域中,内侧索面中斜拉索A'10构件极限承载比最大,为0.87。工况4中,斜拉索高承载构件分布在塔柱附近区域和主跨1/4区域;在塔柱区域中,外侧索面中斜拉索A1构件极限承载比最大,为0.82;在主跨1/4区域中,内侧索面中斜拉索J'12构件极限承载比最大,为0.88。工况5至工况6中斜拉索在极限状态下承载低。不同工况作用下斜拉索的高承载区域构件极限承载比,见表5。

表5 斜拉索高承载区域构件极限承载比
基于上述分析,选取边墩处斜拉索、辅助墩处斜拉索、边跨跨中处斜拉、塔柱处斜拉索、主跨1/4处斜拉索和主跨跨中处斜拉索进行监测,共监测48根斜拉索,斜拉索监测位置,见图8。
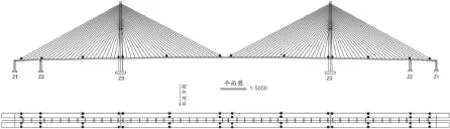
图8 1/2跨斜拉索索力监测位置
3.2 主梁应力监测
工况1中,主梁高承载构件分布在塔柱交接区域和主跨跨中区域,主跨跨中处主梁构件的构件极限承载比最大,为0.98,接近破坏;工况2中,主梁高承载构件分布在辅助墩区域,辅助墩处主梁构件的构件极限承载比等于1,该处构件发生破坏;工况3中,主梁高承载构件分布在辅助墩区域,辅助墩处主梁构件的构件极限承载比等于1,该处构件发生破坏;工况4中,主梁高承载构件分布在塔柱区域和主跨跨中区域,塔柱处主梁构件和主跨跨中处主梁构件的构件极限承载比等于1,该处构件发生破坏;工况6中,主梁高承载构件分布在塔柱交接区域,塔柱交接处主梁构件的构件极限承载比最大,为0.90;工况5中主梁构件在极限状态下承载低。不同工况作用下主梁的高承载区域构件极限承载比,见表6。
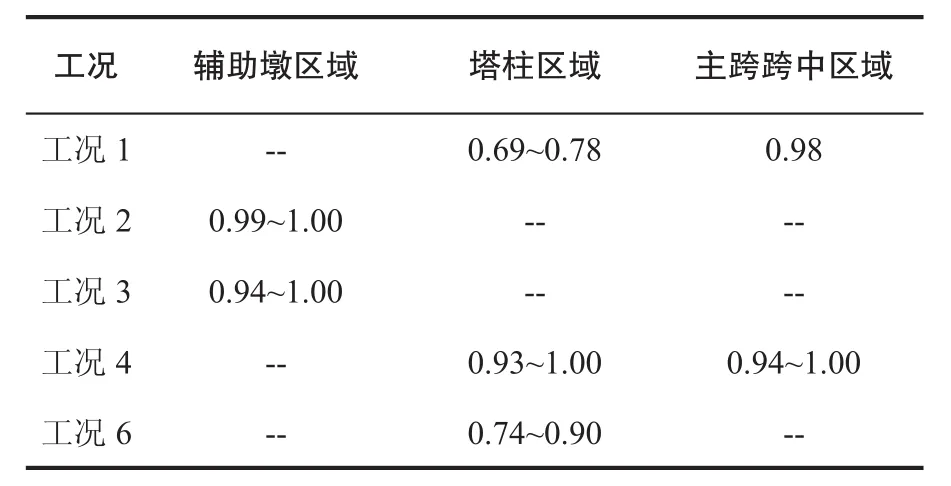
表6 主梁高承载区域构件极限承载比
基于上述分析,选取主跨跨中、塔梁交接处、墩梁交接处等5个关键断面进行应力监测,主梁应力监测位置,见图9。
3.3 主塔应力监测

图9 1/2跨主梁应力监测位置
工况1中,主塔高承载构件分布在中上塔柱交接区域,中上塔柱交接处主塔构件的构件极限承载比等于1,该处构件发生破坏;工况2中,主塔高承载构件分布在上塔柱中间区域,上塔柱中间处主塔构件的构件极限承载比最大,为0.64;工况3中,主塔高承载构件分布在中上塔柱交接区域和中下塔柱交接区域,中下塔柱交接处主塔构件的构件极限承载比最大,为0.71;工况4中,主塔高承载构件分布在下塔柱底部区域,下塔柱底部处主塔构件的构件极限承载比最大,为0.94;工况5中,主塔高承载构件分布在中上塔柱交接区域,中上塔柱交接处主塔构件的构件极限承载比等于1,该处构件发生破坏;工况6中,主塔高承载构件分布在下塔柱底部区域和中下塔柱交接区域,主塔底部和中下塔柱交接处主塔构件的构件极限承载比等于1,该处构件发生破坏。不同工况作用下主塔的高承载区域构件极限承载比,见表7。

表7 主塔高承载区域构件极限承载比
基于上述分析,主塔应力监测断面为:中上塔柱交接处断面、中下塔柱交接处断面、下塔柱底部断面,共6个监测断面,主塔应力监测位置,见图10。
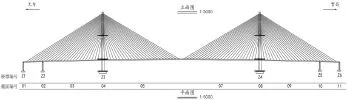
图10 1/2跨主塔应力监测位置
最终基于构件极限承载比的结构内力监测的测试构件数量汇总于表8。从表8可以看出,结构的内力监测共计59个构件。

表8 内力测试构件汇总
4 结论
本文研究了基于极限承载比的大跨度桥梁结构内力监测方案设计。主要结论有:
(1)提出了基于构件极限承载比的大跨度桥梁结构内力监测方案设计方法,定义了构件极限承载比、极限承载比均匀度和基准极限承载比为结构承载特征参数,找出了高承载构件,为桥梁结构内力监测设计提供定量化评价基准。
(2)基于构件极限承载比的结构内力监测所选取的监测构件与结构的真实破坏过程一致,可以减少低承载构件的监测,对于芜湖长江公路二桥可以减少至59个内力监测构件,从而显著的降低了监测费用。
(3)论文提出的基于构件极限承载比的结构内力监测设计理论与方法,仅局限于对桥梁结构内力监测方案的设计。因此,在进行桥梁的健康监测系统设计时,除了内力监测方案,还应根据实际桥梁的其它监测目的来进行桥梁结构的健康监测系统设计。
