双参数地基模型的变截面Timoshenko梁横向振动分析

，

(北京工业大学 建筑工程学院，北京 100124)

1 研究背景

梁作为工程结构的基础构件，被广泛地应用在各种结构中。弹性或者黏弹性地基上的梁构件在工程实际中有着广泛的应用场景，比如铁路轨道、高速公路、人行道和连续管道等。而且对梁进行研究对于研究地基-结构相互作用的机理大有裨益[1]，因此，有很多专家学者研究了基于弹性或黏弹性基础的梁的静力作用[2]、动态响应和动力稳定性等内容。

以弹性地基梁的自由振动分析为例，相当多的学者使用的是Winkler地基模型(或称为单参数模型)，这个模型是捷克工程师于1867年提出的。该模型的特点是把土体视为由一系列侧面无摩擦的土柱或彼此独立的弹簧组成。这种模型的最大缺点是没有考虑土体的连续性，忽略了土体中剪应力的作用。

Eisenberger等[3]研究了局部/整体基于Winkler弹性地基模型的等截面Euler-Bernoulli梁的固有特性。Thambiratnam等[4]对基于Winkler弹性地基模型的梁模型提出了非线性振动分析的解析解；随着研究的深入，发现Winkler模型没有考虑土体连续性的缺点被放大，而且基床系数对结构反应的影响过大。徐牧明等[5]研究了基于室内测试技术快速准确地确定Winkler地基基准基床系数的方法。Valsangkar等[6]研究了基于双参数的弹性地基的等截面梁的运动，对轴向力作用下的简支梁进行了模态分析。De Rosa等[7]考虑了集中质量影响的基于双参数地基模型的Euler-Bernoulli等截面梁的自由振动。刘学山等[8]提出了一个用于分析弹性梁自由振动的新的黏弹性地基模型。

在工程中，出于对力学或美观等方面的考量，梁的截面常常被设计成变截面。这会使得运动方程变为变系数的偏微分方程组，使求梁自由振动解析解变得困难，所以通常是采用半解析解或由数值方法得到的近似解来分析。对变截面梁动力特性的分析方面，楼梦麟等[9]提出了利用等截面梁的动力特性来近似计算变截面梁的动力特性的方法；崔灿等[10]提出了基于平衡方程的任意变截面梁横向振动的半解析解。

本文采用的Pasternak弹性地基模型(又称双参数地基模型)用2个独立的参数分别表示土体的抗压特征系数k和抗剪特征系数Gp，该模型既克服了Winkler地基模型不能反映压力扩散的缺陷，数学处理上又较弹性半空间地基模型简单。

本文将基于Timoshenko梁理论[11]、Pasternak双地基模型和哈密顿原理，运用数学中的分段[12]思想，将每个有限元单元都视为一个等截面梁段，用有限元法[13]快速地计算变截面梁(以渐缩梁为例)的横向振动特性。

2 控制方程

2.1 单元矩阵生成

有限长Timoshenko梁完全置于Pasternak地基上，长度为L，见图1。这里，每个梁单元由2个节点i，j组成，每个节点包含2个自由度：侧向位移υe和转角θe。此外，以下的推导基于如下几点假设：①梁的振动幅度足够小；②梁的材料是各向同性且线性的；③忽略基础的惯性力和阻尼；④梁和地基完美结合。

图1 Pasternak双参数地基Fig.1 Sketch of beam on Pasternak foundation

在不考虑外界荷载作用的情况下，梁的运动方程为

(1)

式中：0≤x≤L；y=y(x,t)，为梁的横向挠度函数；EI(x)为横向弯曲刚度；ρA(x)为线密度；k为土体的抗压特征系数(由图1中的弹簧提供)；Gp为土体抗剪特征系数(由图1中的剪切层提供)。

使用分离变量法，得到对应振型函数的四阶常微分方程,即

(2)

本文将基于β=1.0，即图1对应的情况展开研究。解的情况需要根据η4的取值来定，分成以下3种情况：①η4>0；②η4=0；③η4<0。

显然，无法根据式(2)得到变截面梁的解析解，也无法应用此式对变截面梁进行进一步的动力特性分析(如模态分析)。

这里，基于分段的思想，将变截面梁分为相互连接、满足位移协调条件的N个梁段的组合体(本文采用的是长度相等，高度沿轴向变化的梁段)。当段数足够多时，可以将每一梁段都看作是等截面梁，如图2。

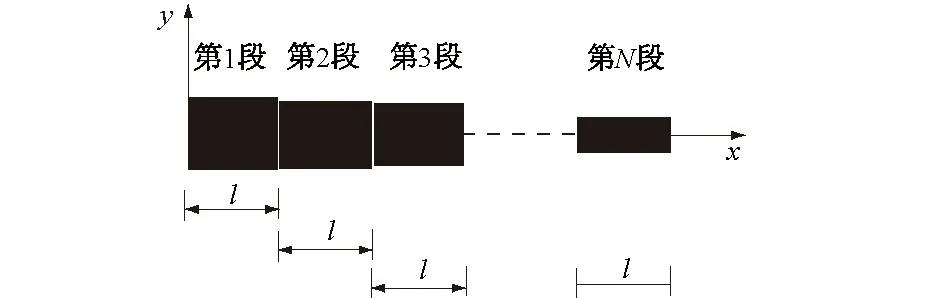
图2 分段梁单元Fig.2 Divided beam with N segments

基于哈密顿原理(Hamilton’s principle)，对每个长度为l的梁段，考虑剪切变形影响及弹性地基作用的应变能Ue可以写成如下的形式，即

(3)

式中：E为弹性模量；I为梁的惯性矩；k′为等效截面剪切系数(矩形截面取5/6)；G为剪切模量；A为横截面面积。

考虑转动惯量的动能Te表示为

(4)

式中ρ为梁的质量密度。根据有限元法，单元的位移模式应满足完备性和协调性。节点处的横向位移和转角分别表示为υi，θi。这里选择单元位移模式为三阶多项式函数(其中θ(x)是考虑剪切变形影响的位移模式)：

υ(x)=a+bx+cx2+dx3;

(5)

(6)

式中a，b，c，d为广义坐标。单元的节点位移可表示为

(7)

将单元节点坐标代入式(5)、式(6)，用矩阵表示为

(8)

解方程(8)，求广义坐标用节点自由度υi和θi表示的形式，再将其代入式(5)、式(6)，可表示为：

(9)

(10)

其中，插值函数(形函数)[Nυ]内的每项为：

(11)

(12)

(13)

(14)

插值函数(形函数)[Nθ]内的每项为：

(15)

(16)

(17)

(18)

由于Timoshenko梁单元的性质，弯曲应变和剪切应变分别表示为：

(19)

(20)

其中：

(21)

(22)

将式(9)、式(10)代入应变能Ue、动能Te表达式，可以得到应变能和动能的矩阵形式：

(23)

(24)

需要注意的是，如果剪切应变γ为0，那么转动惯量对应的质量矩阵[Mr]将被忽略，并且此时的模型变为由Karamanlidis等[14]提出的经典Euler-Bernoulli梁模型在双参数弹性地基梁的形式。

2.2 控制方程生成

根据之前生成的单元刚度矩阵，应用哈密顿原理，满足小变形的自由振动的基于二参数的弹性地基Timoshenko梁的矩阵方阵为

(25)

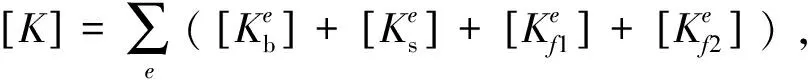
通过对式(25)特征值的求解(运用矩阵QR分解)，得出对应的各阶频率和模态。

3 数值算例

以2种变截面梁为算例，讨论有限单元个数对计算精度的影响。在有限元中，采用的是两节点平面梁单元模拟梁的横向振动，单元数分别为40，80，200，500。

3.1 矩形截面梁算例

取全部作用在Pasternak地基上(β=1.0)且两端简支有限长梁(截面为矩形)为算例，参数为：梁长L=4 m，截面宽度b=0.4 m，第1个梁单元高度hi=0.6 m，he=0.3 m为最后一个梁单元的高度，泊松比υ=1/3，等效截面剪切系数k′=5/6，弹性模量E=210 GPa，体密度ρ=7 900 kg/cm3，土体抗压缩刚度系数k= 80 MPa，抗剪压缩刚度Gp=750 kN。图3为高度线性变化的宽度不变的矩形截面梁示意图。

图3 高度线性变化的矩形截面梁Fig.3 Linear change of the height of rectangular cross-sectional beam

表1给出了选取不同单元个数时弹性地基梁上矩形变截面简支梁的前5阶固有频率，并且和已有文献提出的方法进行对比。可以看出，随着单元数目的增加，频率逐渐增加，这与曹长勇等[15]提出的用傅里叶变换求解的Pasternak地基上梁振动的解析解接近，证明此有限元模型是可靠的。

表1 双参数弹性地基上矩形变截面Timoshenko梁固有频率Table 1 Comparison of natural frequencies for fully supported rectangular beam between finite element and available results

3.2 圆形截面梁算例

取全部作用在Pasternak地基上(β=1.0)且两端简支有限长梁(截面为圆形)为算例，参数为：梁长L=4 m，最左边的梁截面直径di=0.6 m，de=0.3 m为最右边的梁截面直径，其他参数同3.1节。梁截面变化见图4。

图4 半径线性变化的圆截面梁Fig.4 Linear change of the radius of circlecross-sectional beam

表2给出了选取不同单元个数时弹性地基梁上圆形变截面简支梁的前5阶固有频率，并且和已有文献提出的方法进行对比。

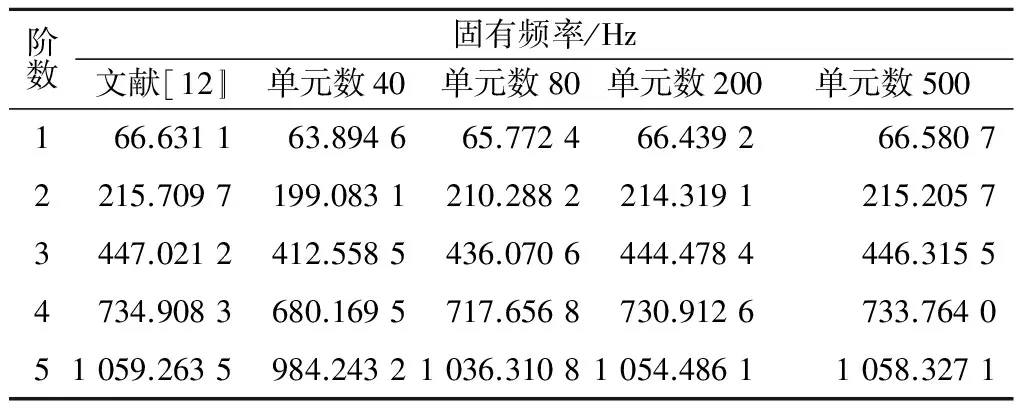
表2 双参数地基上圆形变截面Timoshenko梁固有频率Table 2 Comparison of natural frequencies for fully supported circular beam between finite element and available results

4 结 论

基于Timoshenko梁理论和Pasternak双参数地基模型，利用Hamilton原理建立了能量方程，并依据有限元方法对其进行求解，丰富并完善了求解全支撑于弹性地基的变截面梁(β=1.0)的数值方法。构建了在弹性地基上每个单元的弹性刚度矩阵和地基提供的刚度矩阵。由矩形截面梁和圆形截面梁2个算例可知，随着单元划分越精细，地基梁结构的模态反应跟半解析解越接近。对分析人员来说，只需确定地基梁结构的各项参数和划分单元数量，就可以直接计算求得分析结果，具有省时高效的优点。这表明了完善后的数值方法的高效性和准确性。

此外，本方法除了用于弹性地基外，还可以用于黏弹性地基等地基模型，因此有着广泛的适应性。

[1] SELVADURAI A P S. Elastic Analysis of Soil-Foundation Interaction [M]. Amsterdam: Elsevier, 1979.

[2] 卢 健,温中华,周 娟.弹性地基梁法计算地下钢筋混凝土岔管结构应力[J].长江科学院院报,2008,25(1):80-81.

[3] EISENBERGER M, YANKELEVSKY D Z, ADIN M A. Vibrations of Beams Fully or Partially Supported on Elastic Foundations[J].Earthquake Engineering and Structural Dynamics,1985,13(5):651-660

[4] THAMBIRATNAM D,ZHUGE Y.Free Vibration Analysis of Beams on Elastic Foundation[J].Computers and Structures,1996, 60(6):971-980.

[5] 徐牧明，陈定安.一种新型的基准基床系数室内通用测试方法[J].长江科学院院报，2017，34(1):109-113.

[6]VALSANGKAR A J, PRADHANANG R. Vibrations of Beam-columns on Two-parameter Elastic Foundations[J].Earthquake Engineering and Structural Dynamics, 1988, 16(2):217-225.

[7] DE ROSA M A, MAURIZI M J. The Influence of Concentrated Masses and Pasternak Soil on the Free Vibrations of Euler Beams—Exact Solution[J]. Journal of Sound and Vibration, 1998, 212(4):573-581.

[8] 刘学山,冯紫良,胥 兵.粘弹性地基上弹性梁的自由振动分析[J].上海力学,1999,20(4):470-476.

[9] 楼梦麟,沈 霞.弹性地基梁振动特性的近似分析方法[J].应用力学学报,2004,21(3):149-152.

[10] 崔 灿,蒋 晗,李映辉.变截面梁横向振动特性半解析法[J].振动与冲击,2012,31(14):85-88.

[11] TIMOSHENKO S P. Vibration Problems in Engineering[M]. 2nd Edition. New York: Wolfenden Press, 2008.

[12] GUPTA A K. Vibration of Tapered Beams[J]. Journal of Structural Engineering, 1985, 111(1):19-36.

[13] YOKOYAMA T. Vibrations of Timoshenko Beam-columns on Two-parameter Elastic Foundations[J]. Earthquake Engineering and Structural Dynamics, 1991, 20(4):355-370.

[14] KARAMANLIDIS D, PRAKASH V. Exact Transfer and Stiffness Matrices for a Beam/column Resting on a Two-parameter Foundation[J]. Computer Methods in Applied Mechanics and Engineering, 1989, 72(1):77-89.

[15] CAO Chang-yong, ZHONG Yang. Dynamic Response of a Beam on a Pasternak Foundation and under a Moving Load[J].Journal of Chongqing University (English Edition),2008,7(4):311-316.