基于尺寸效应的类岩石材料点荷载指标与单轴抗压强度对应关系研究

， ，，

(1. 绍兴文理学院 a. 土木工程学院; b.岩石力学与地质灾害实验中心，浙江 绍兴 312000;2. 浙江省交通规划设计研究院，杭州 310000)

1 研究背景

单轴抗压强度作为岩石材料的基本力学参数，广泛应用于岩体质量分级、隧道等各类岩体工程建设及边坡稳定性评估中。国内外长期以来多采用室内力学试验来获取岩石单轴抗压强度，包括直接法与间接法。其中，直接法可以精确获取岩石强度参数，但需要制作标准试件[1-2]，这就面临试验成本高、试验费时、费工等问题。在一些特殊条件下，如断层带、强风化岩体和软岩等，制作标准岩石试件十分困难；对层片状岩体，单轴抗压强度试验结果受试件结构各向异性影响显著；单轴压缩试验无法满足工程现场及时进行岩石强度特性描述的要求等，使直接法测量呈现一定的局限性。

为了克服直接法的局限，一系列间接测试方法开始被用于估算岩石单轴抗压强度[3-5]，其中岩石点荷载试验具有易操作、可测不规则试件、时间短、费用低、可靠性较高等优点，尤其适应工期紧张、需进行孔底岩石鉴别、现场岩石强度描述等情况。国际岩石力学学会(ISRM)试验方法委员会在1972年布鲁克(E. Broch)和弗兰克林(J.A.Franklin)发明此法时即建议采用[6]，并于1985年对其进行了修正[1]。一直以来点荷载试验被认为是一种现场测定、估算单轴抗压强度的最佳方法[7-9]。20世纪70年代以来，岩石点荷载试验一直受到国际岩石力学界和工程界的普遍关注，大量的学者进行了点荷载强度指标与单轴抗压强度之间的相关性研究，即强度转换因子的确定及敏感性分析，并取得了丰硕的研究成果(见表1)。

通过总结大量相关文献发现，将所有岩石强度转换关系用一个关系式表达时相关系数会很低，在实际的应用过程中会产生较大误差[10]。因此前人的研究成果大都根据岩石的种类确定不同的统计关系式，当试验数据细分至不同岩石类型(岩浆岩、沉积岩与变质岩)以及不同岩石亚类进行单独等式回归分析会显著提高相关系数[11]。岩石的强度主要取决于岩石的地质成因，诸如地质构造、风化程度等因素影响。因此强度转换因子必然受到矿物颗粒组成、结构面发育程度、孔隙率等特征影响[12]，呈现显著的各向异性特征。与此同时，强度转换因子具有很强的地域性，多数转换公式只是针对某个国家或地区使用。

表1 岩石点荷载强度指标Is(50)和单轴抗压强度Rc的统计关系

续表1

函数类型编号 作者 方程相关系数R指数函数30Diamantisetal．(2009)[4〛Rc=16．45exp(0．39Is(50))0．8931Kahraman(2014)[30〛Rc=2．68exp(0．93Is(50))0．93Rc=1．99exp(1．18Is(50))0．92Rc=2．27exp(1．04Is(50))0．93对数函数32Kilicetal．(2008)[34〛Rc=100lnIs(50)+13．90．9933Kahraman(2014)[30〛Rc=17．04lnIs(50)+9．290．75Rc=7．27lnIs(50)+11．700．75Rc=10．28lnIs(50)+12．320．73二次函数34QuaneandRussel(2003)[17〛Rc=3．86(Is(50))2+5．56Is(50)—35张建明，唐志成等(2015)[35〛Rc=3．86(Is(50))2+5．56Is(50)0．94

注：Is(50)为经修正后直径为50 mm的标准试件的点荷载强度指标

综上分析可以得出，目前对于点荷载指标与单轴抗压强度之间的转换因子统计分析尚存在4个方面的问题：①岩石材料的各向异性特性很难建立适用于所有岩石的点荷载指标和单轴抗压强度的关系；②大量的学者在建立了经验转换关系公式后没有就实际情况再进行试验验证；③文献中的试验数据不是一一对应的关系，并且未注明不规则试件的尺寸等，无法建立非标准点荷载间距在50 mm以下的尺寸效应和对应关系；④就点荷载试验仪器本身来说，设备笨重给技术人员在现场进行大量对应试验带来不便。

基于上述观点，本文采用各向同性的类岩石材料(水泥)制作不同标号强度、不同尺寸的试件，共计931块。利用自行研制的便携式点荷载仪进行点荷载强度测试，结合单轴抗压强度试验进行一一对应的相关性统计分析，确定强度转换因子及转化关系。最后通过对不规则试件的点荷载试验，验证关系公式的准确性。

2 便携式点荷载试验机

点荷载试验是将岩石试件置于上、下2个球状圆锥加载头之间，对试样施加集中荷载，直至破坏，根据压力传感器记录下的压力值求得岩石点荷载强度，再通过经验系数确定岩石的抗压强度值。破坏机理为距离加载头一定范围内对岩石形成压应力区，而距加载头一定距离之外岩石则受到垂直于加载轴方向的弹性拉应力作用。随着荷载增大，则在加载头附近产生的弯曲排列的雁行式裂隙会不断相互靠拢形成滑移线，裂纹逐渐扩展，并最终与弹性拉应力区相连接，即试件在拉应力作用下发生劈裂破坏[36]。

工程领域内现有的点荷载仪器均比较笨重，无法满足技术人员方便携带至现场使用的要求。因此我们按照ISRM对加载头的要求(直径10 mm，顶角60°)，设计制作了便携式岩石点荷载仪(见图1)。该设备可以满足岩石强度在150 MPa以内的点荷载现场测试，既适用于室内测量标准尺寸的圆柱体试件，又能实现厚度为10～50 mm的不规则试件的现场测量，质量为10 kg，几何尺寸为(长×宽×高)180 mm×185 mm×400 mm，其主要技术参数如表2所示。

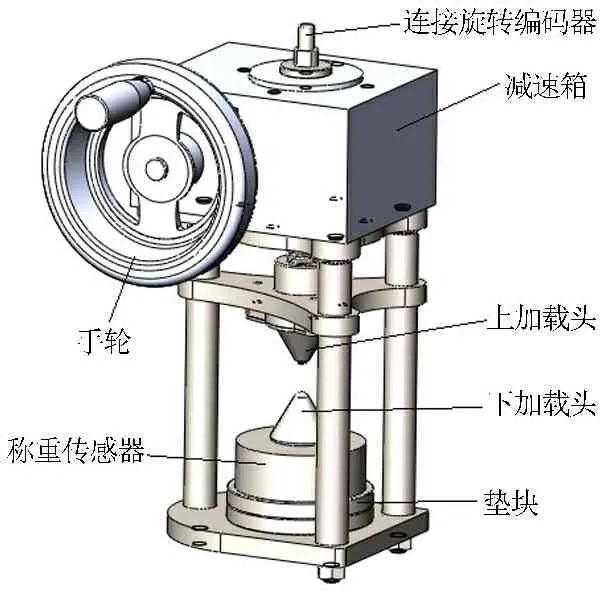
图1 便携式岩石点荷载仪示意图

3 试验材料与试验方法

3.1 试件制备

点荷载试验对岩石试件尺寸的要求，根据国际岩石力学试验委员会建议的方法和国内标准，主要有圆柱样、方块样、不规则样。许多学者就点荷载试件的尺寸和形状对点荷载强度值的影响做了大量的试验研究，在试验中发现，岩石点荷载强度值随着试件的面积、点间距以及体积的增大，变化在一定范围时，存在一个稳定的区间。同时，由于野外勘察通常没有现成的岩芯可用，更多的情况需要针对不规则试件。因此，对于不规则试件的尺寸选取应在稳定区域范围内进行测试，方可避免产生数据的起伏和离散，这能为技术人员现场对点荷载试件的选取提供参考从而提高试验结果的准确性。从文献中归纳了前人对点荷载试件尺寸选取的研究，见表3。

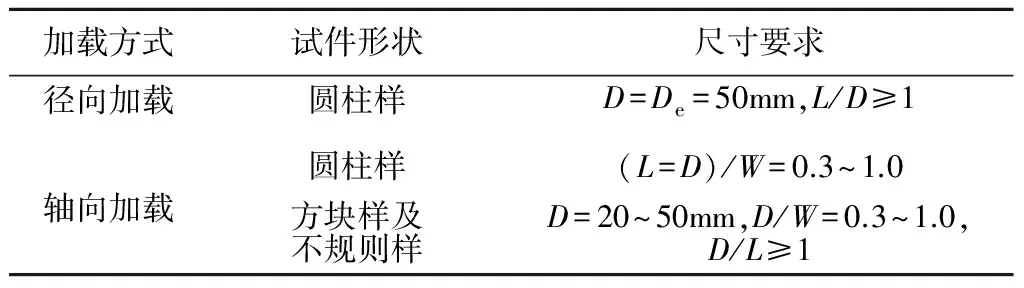
表3 点荷载试件尺寸的建议[36-41]

注：表中D为加载点间距离；De为等效直径；L为试件长度；W为通过两加载点最小截面的宽度

(a)水泥板养护(b)32．5R方样(c)42．5方样(d)52．5方样

图2不同尺寸、标号水泥试件制备

Fig.2Preparationofdifferent-gradecementspecimenswithdifferentsizes

为避免试件形状、尺寸带来的影响，制作了边长为20～50 mm不等的立方体水泥试件。同时，为了模拟不同岩石的强度形成对比区分，我们选取了标号分别为32.5R，42.5，52.5的水泥，按水灰比为0.3进行拌制浇筑，并在标准条件下养护28 d，制作出530 mm×345 mm×70 mm(长×宽×高)的水泥板26块，见图2(a)。利用红外控制切割机切割出不同尺寸的试件，误差±0.1 mm，见图2中的(b)—(d)。用于标准单轴抗压强度测试的水泥试件，按照《建筑砂浆基本性能试验方法标准》(JGJ/T 70—2009)的规定制作成70.7 mm×70.7 mm×70.7 mm的立方体，并保证试件的不平度控制在每100 mm不超过0.05 mm，两相邻面的不垂直度不超过±5°，每组3个立方体试件，每种标号水泥分别制作2组，共计6组。最终用于点荷载和单轴抗压强度试验试件共计931个，具体尺寸见表4。

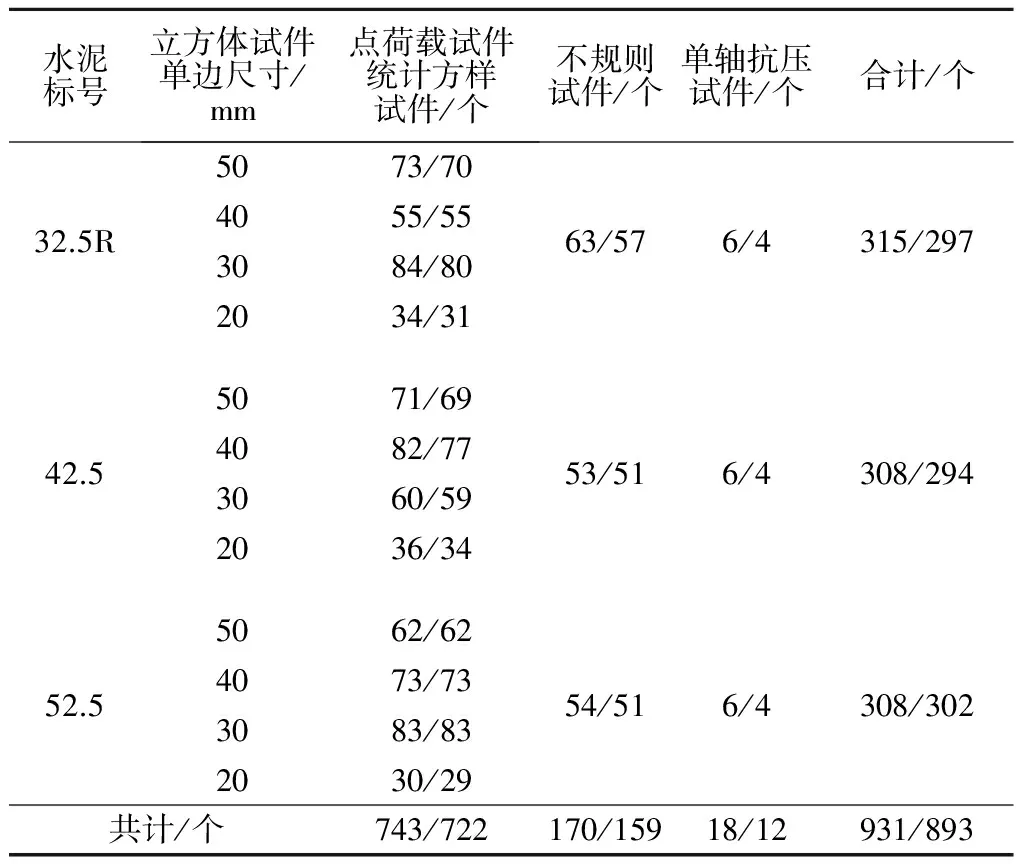
表4 试件数量统计

注： “/”左侧数据代表试验准备试件个数， 右侧数据代表试验有效试件个数

3.2 试验方法及计算公式

3.2.1 点荷载指标确定

点荷载试验通过破坏荷载值及相关尺寸即可求得岩石点荷载指标。根据张国锋等[42]、戴洪军等[43]对岩石点荷载强度计算公式的研究发现，岩石点荷载强度计算采用压点接触面积求等效直径的计算方法，具有明确的物理意义，即试样在点荷载作用下单位破坏面积上所能承受的最大荷载。该方法物理意义明确、具有强度单位、计算简便、误差小，得到业界普遍的认可。因此，本文采用这种方法并结合ISRM法、《工程岩体分级标准》(GB/T 50218—2014)、《工程岩体试验方法标准》(GB/T 50266—2013)等规范的规定，对方块样和不规则试件的点荷载指标进行计算。根据ISRM法公式有：

Is(50)=IsF;F=(De/50)0.45。

(1)

式中：Is为未经修正的点荷载强度指数；P为破坏荷载；F为尺寸效应修正系数。

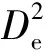
Is(50)=P50/2 500 。

(2)

3.2.2 单轴抗压强度确定

由于本次对比试验仅针对水泥材料，故根据《建筑砂浆基本性能试验方法标准》(JGJ/T 70—2009)规定制作水泥立方体。单轴抗压强度为边长70.7 mm立方体在无侧限条件下所能承受的荷载。将试件置于万能试验机承压板中心，调整球形座，使试件两端面与试验机上下承压板接触均匀，然后以1.5 kN/s的速度加载直至试件破坏，同时记录破坏荷载及加载过程出现的现象。立方体水泥试件单轴抗压强度按式(3)计算，即

Rc=P/A。

(3)

式中：Rc为立方体单轴抗压强度(MPa)；A为试件承压面积(mm2)。

此次对比试验选用了3种不同标号水泥制作了不同尺寸的方样试件，具体见表4。

4 试验数据处理

点荷载试验有效数据均来自点荷载作用下试件形成贯穿裂缝的试件，部分破坏试件见图3，无效试件则是表面有清晰可见的裂缝或是点荷载试验过程中未加压即崩解，未形成贯穿裂缝等情况。单轴抗压强度试验有效数据均来自试验完成后试件形成贯穿裂缝所承受的最大的破坏荷载值，并舍弃试验测得的最大、最小破坏荷载值。

图3部分试件破坏情况

Fig.3Damageofsomesamples

4.1 数据统计分析与评价

首先按不同标号强度的水泥分类对所有试验数据进行频率直方图绘制和正态分布统计，如图4所示。

(a)标号32.5R的试件

(b)标号42.5的试件

(c)标号52.5的试件

图4不同标号水泥的点荷载强度频率直方图和正态分布曲线

Fig.4Histogramandnormaldistributioncurveofpointloadintensityfrequencyofdifferent-gradecementspecimens

点荷载强度指标频率直方图能够很好地符合正态分布规律。由统计学知识可知，只有当数据符合这种对称分布尤其是正态分布规律时，其样本平均数才能很好地代表总体数据水平和数据的集中程度，因此该试验数据是科学可信的。从图4提取标号分别为32.5R，42.5，52.5水泥试件的最大频率所对应的强度范围分别为2.0～2.5 MPa，1.75～2.25 MPa ，2.38～3.00 MPa。可以看出，标号越高的水泥试件则点荷载强度指标也越高，试验数据符合实际规律。采用变异系数，即试验数据的标准差与平均值的比值，评价试验数据的偏离程度。结合点荷载强度指标统计(见表5)，32.5R，42.5，52.5水泥的变异系数分别为0.352，0.367，0.169，说明水泥试件的点荷载指标具有较好的稳定性，并且随着水泥标号的提高，点荷载强度指标也愈加稳定。

表5 点荷载试验强度值统计

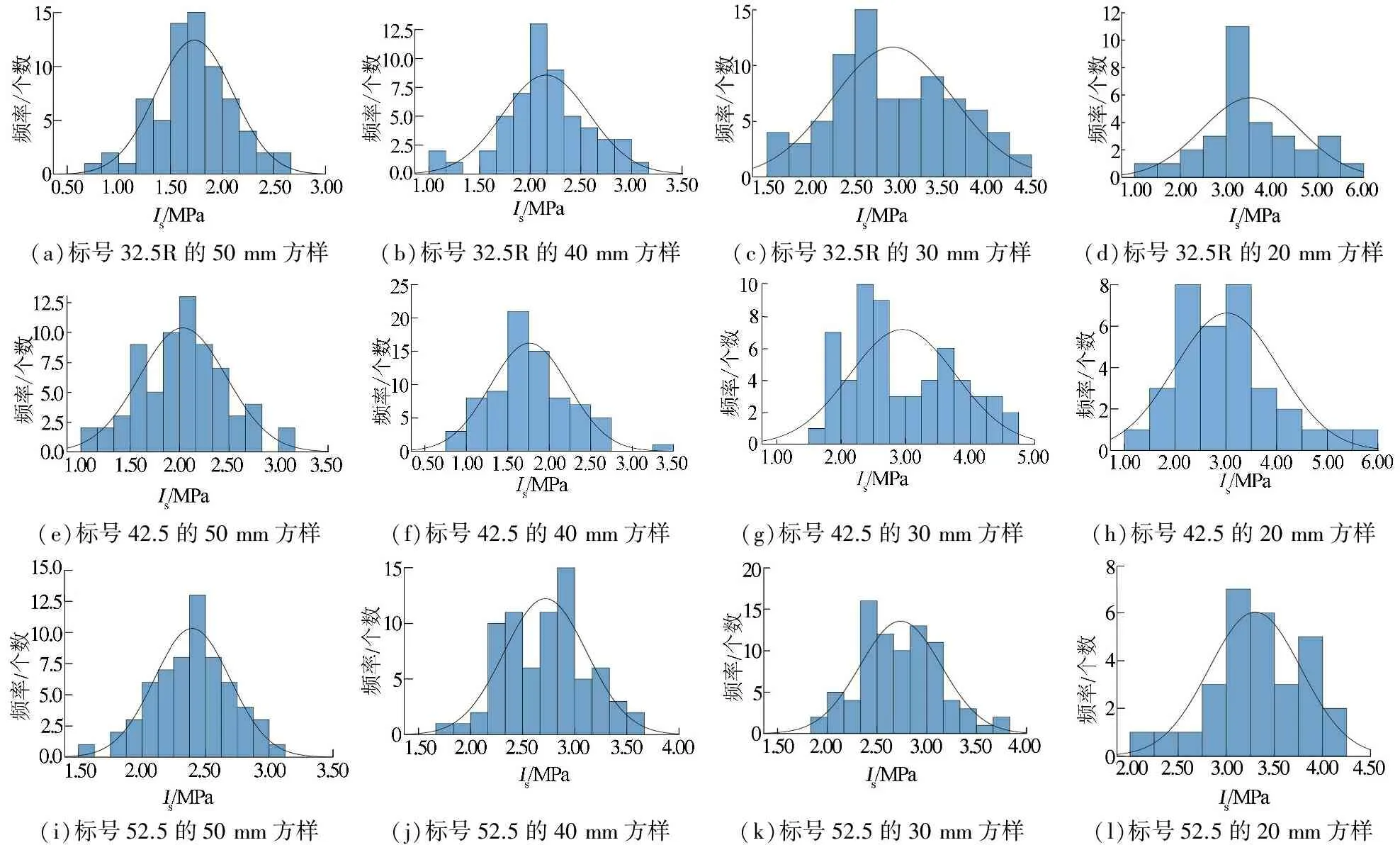
(a)标号32．5R的50mm方样(b)标号32．5R的40mm方样(c)标号32．5R的30mm方样(d)标号32．5R的20mm方样(e)标号42．5的50mm方样(f)标号42．5的40mm方样(g)标号42．5的30mm方样(h)标号42．5的20mm方样(i)标号52．5的50mm方样(j)标号52．5的40mm方样(k)标号52．5的30mm方样(l)标号52．5的20mm方样

图5不同尺寸试件的点荷载强度频率直方图和正态分布曲线

Fig.5Histogramandnormaldistributioncurveofpointloadintensityfrequencyofdifferent-sizespecimens

为了描述不同尺寸点荷载试验数据的可靠程度和集中程度，仍需对不同尺寸试件的点荷载强度指标进行频率直方图和正态分布规律进行统计，具体结果如图5所示。根据频率直方图可以看出，所测试验数据基本均符合正态分布规律。标号32.5R和42.5的尺寸为30 mm的样品试验数据虽存在不符合正态分布规律的部分，这是由于不同尺寸分类时样本数量大量减少所致，总体仍靠近正态分布峰值，与峰值偏差0.1 MPa，并不影响整体符合正态分布的规律。

从图5对3种标号水泥不同尺寸试件的点荷载试验可以看出，图5中(a)—(d) 32.5R水泥试件尺寸为50，40，30，20 mm，最大频率强度范围分别为1.50～1.82 MPa，2.00～2.32 MPa，2.25～2.75 MPa，3.0～3.5 MPa；图5中(e)—(h) 42.5水泥试件尺寸为50，40，30，20mm，试件最大频率强度范围分别为1.84～2.16 MPa，1.5～2.0 MPa，2.25～2.75 MPa，2.5～3.5 MPa；图5中(i)—(l) 52.5水泥试件尺寸为50，40，30，20 mm，试件最大频率强度范围分别为2.38～2.50 MPa，2.66～3.00 MPa，2.34～3.00 MPa，3.0～3.5 MPa。结合表5中未经修正的点荷载强度指标均值Is的取值发现，相同标号水泥制作的不同尺寸试件的点荷载强度指标具有明显的尺寸效应，即随着水泥试件尺寸在点荷载标准尺寸间距50 mm以下不断减小，相应的点荷载强度指标随之增大。这种效应在3种不同标号水泥中均得到很好的验证。

同时，我们对不同标号和每种标号的不同尺寸的水泥样品试验数据进行离散程度、变异程度、置信度的检验分析，统计结果见表5。点荷载强度指标符合正态分布规律，故均值能够很好地反映每个标号水泥的总体点荷载强度值。通过分析试验数据的标准差可见，每种水泥试件的离散程度随着试件尺寸的减小而增大，其中在40，50 mm时的标准差最小，故在实际应用中应多采用尺寸在30～50 mm的试件。

同时变异系数也存在相同规律，但数值增大的幅度非常小，尤其较岩石材料点荷载的变异程度幅度3.6%(花岗岩)～33.4%(英安岩)[36]而言相当小，因此在工程实践中是可以接受的。最后对点荷载实际强度范围进行估计，表5采用置信水平α=0.05，置信度95%时的置信区间[44-45]，可以看出各试件强度指标均在置信区间范围内，且置信区间长度最大不超过0.2 MPa，精度高。随着水泥标号的增大，点荷载指标的精度也随之提高，可信度更高。

表6 试验结果汇总

根据相关系数R最大的原则确定相关性表达式，见图6。分析表明，线性函数和对数函数均达到统计学表达的2个变量强相关性的要求R∈(0.7,1)。但进一步观察能够发现，线性函数很好地穿过了不同尺寸实测值最密集区域，对应的就是点荷载强度最集中的区域，线性关系能够更加符合实际情况。随着水泥标号的提高，线性函数的相关系数不断提高，在标号52.5水泥试件中R=0.97，最终本文采用线性函数表达并利用式(2)直接计算出Is(50)，结果如表6所示。

(a)标号32.5R试件

(b)标号42.5试件

(c)标号52.5试件

4.2 经验关系建立

素水泥试件单轴抗压强度取值依据《建筑砂浆基本性能试验方法标准》(JGJ/T 70—2009)规定舍弃最大最小值，将剩余测值的算术平均数的1.3倍作为该组素水泥立方体试件的抗压强度平均值。

Rc=29.87Is(50)-2.242 。

(4)

4.3 试验验证

通过水泥这种类岩石材料制作大量不同标号强度、不同尺寸的试件，本文进行了上述点荷载试验和单轴抗压强度试验，并建立了相应的转换公式。为了更好地证明此公式的可信度，又从同一批水泥板中制作了大量不规则试件，按照上述方法进行不规则试件的点荷载验证试验。不同标号水泥的不规则试件共计170个(见表3)，不规则试件破坏前后对比图像见图7。验证所得的点荷载强度指标与式(4)计算出的单轴抗压强度公式的验证结果见表7。

(a)标号32.5R试件 (b)标号42.5试件 (c)标号52.5试件

注：上部分为破坏前，下部分为破坏后

通过表7的验证结果对比分析能够看出，从同一批水泥板中制作的不规则试件的点荷载强度指标经式(4)计算的单轴抗压强度与实测值的误差在15%以内。如果能够制作更多的不规则点荷载试件，对于水泥材料而言这个误差可以进一步缩小。这个误差比岩石实测值与计算值误差(一般为20%)要小[45-46]，验证了式(4)的可信度，同时也证明点荷载试验的可靠度。

5 工程实例验证

关山隧道穿越关山中山的山地区，属六盘山山脉。隧道洞身以N46°E走向穿越关山，经过地区地面高程1 694.8～2 607.8 m，最大埋深831 m。隧道在大地构造上地处六盘山褶皱带之次级构造单元关山褶皱带。关山褶皱带位于通渭—清水断层和庄浪—固光断层之间。关山隧道通过区侵入岩为大面积华力西期，呈巨大的岩基产出，伴生有小岩体。

现场取样用于点荷载试验的岩石为闪长岩，青灰色，细粒—中粗粒结构，块状构造，岩体节理发育。该类岩石的造岩矿物主要包括石英、斜长石、黑云母和副矿物磁铁矿、锆石、磷灰石等。

针对关山隧道的中粒闪长岩进行了点荷载试验19次，单轴抗压强度试验6次，点荷载试验破坏过程见图8。通过对试验数据统计分析，得到该工程现场岩石点荷载试验数据的变异系数为0.286，在置信度95%时的置信区间为[5.137,6.938]。与水泥试件的点荷载试验的变异系数及置信区间范围相比，离散程度有所扩大，这是由于关山隧道的闪长岩受到褶皱构造、不同矿物成分的影响造成岩石材料的各向异性导致的。

图8闪长岩不规则试件破坏过程

Fig.8Failureofdioriteirregularspecimens

结合单轴抗压强度的试验数据，进行了回归拟合分析，见图9，为了工程实际的快速应用，选择线性相关系数为0.93的关系式快速估测岩石单轴抗压强度值，该法比ISRM推荐的范围关系式更加精确合理。

图9闪长岩点荷载值与单轴强度值关系曲线

Fig.9Relationshipbetweenpointloadvalueanduniaxialstrengthofdiorite

6 结 论

(1)通过自制便携式点荷载仪器对类岩石材料进行了大量点荷载试验，获得试验数据符合正态分布规律，集中趋势显著。建立了点荷载指标与单轴抗压强度相关系数R=0.994的线性关系式，提出了利用加载点间距≤50 mm的试件估算单轴抗压强度的可靠度。便携式设备可以通过随机选择不规则试件(D≤50 mm)进行点荷载试验，用于工程现场快速测定岩石强度。

(2)通过931块不同尺寸的试件分析点荷载指标的尺寸效应试验表明，随着选取的岩石试件尺寸的减小，岩石点荷载强度增大，尺寸效应显著。选取两加载点间距在40～50 mm的试件，试验数据集中趋势更明显，离散程度最小。因此现场应注意试件的尺寸选取以提高点荷载强度的测试精度。

(4)本文试验数据具有一一对应性，克服了大量文献中的试验数据仅能做到模糊对应的局限性。利用点荷载指标估算单轴抗压强度的计算值与实测值比较，通过对不规则的类岩石试件、岩石试件进行了试验验证，误差在15%以内，证明了点荷载试验的工程适应性。

[1] FRANKLIN J A. ISRM Suggested Method for Determining Point Load Strength[J]. International Journal of Rock Mechanics and Mining Sciences,1985,22(2):51-60.

[2] ASTM D5731, Standard Test Method for Determination of the Point Load Strength Index of Rock and Application to Rock Strength Classifications[S]. Pennsylvania: American Society for Testing and Materials, 2016.

[3] AZIMIAN A, AJALLOEIAN R, FATEHI L. An Empirical Correlation of Uniaxial Compressive Strength with P-wave Velocity and Point Load Strength Index on Marly Rocks Using Statistical Method[J]. Geotechnical and Geological Engineering, 2014, 32(1): 205-214.

[4] DIAMANTIS K, GARTZOS E, MIGIROS G. Study on Uniaxial Compressive Strength, Point Load Strength Index, Dynamic and Physical Properties of Serpentinites from Central Greece—Test Results and Empirical Relations[J]. Engineering Geology, 2009, 108(3): 199-207.

[5] KARAKUL H. Investigation of Saturation Effect on the Relationship Between Compressive Strength and Schmidt Hammer Rebound[J]. Bulletin of Engineering Geology and the Environment, 2017, 76(3): 1143-1152.

[6] BROCH E, FRANKLIN J A. The Point Load Strength Test[J]. International Journal of Rock Mechanics and Mining Sciences, 1972, 9: 669-676.

[7] GOUDIE A S. Schmidt Hammer in Geomorphological Research[J].Progress in Physical Geography,2006,30(2):703-716.

[8] KABILAN N, MUTTHARA M, SIVA A,etal. Prediction of Uniaxial Compressive Strength Using Point Load Index for Jointed Rocks[J]. Journal of Mechanical and Civil Engineering,2016,13: 1-7.

[9] KAHRAMAN S, GUNAYDIN O, FENER M. The Effect of Porosity on the Relation between Uniaxial Compressive Strength and Point Load Index[J]. International Journal of Rock Mechanics & Mining Sciences,2005,42(4):584-589.

[10] KAYA A, KARAMAN K. Utilizing the Strength Conversion Factor in the Estimation of Uniaxial Compressive Strength from the Point Load Index[J]. Bulletin of Engineering Geology and the Environment, 2016， 75(1): 341-357.

[11] KAHRAMAN S, GUNAYDIN O. The Effect of Rock Classes on the Relation Between Uniaxial Compressive Strength and Point Load Index[J]. Bulletin of Engineering Geology and the Environment, 2009,68(3):345-353.

[12] TANDON R S, GUPTA V. Estimation of Strength Characteristics of Different Himalayan Rocks from Schmidt Hammer Rebound, Point Load Index, and Compressional Wave Velocity[J]. Bulletin of Engineering Geology and the Environment, 2015,74(2):521-533.

[13] BIENIAWSKI Z T. The Point Load Test in Geotechnical Practice[J]. Engineering Geology,1975,9(1):1-11.

[14] READ J R L, THORNTEN P N, REGAN W M. A Rational Approach to the Point Load Test[C]∥Institution of Professional Engineerings New Zealand,Third Australia-New Zealand Conference on Geomechanics, Wellington, May 12-16, 1980: 35-39.

[15] GHOSH D K, SRIVASTAVA M. Point-load Strength: An Index for Classification of Rock Material[J]. Bulletin of the International Association of Engineering Geology, 1991,44(1): 27-33.

[16] CHAU K T,WONG R H C.Uniaxial Compressive Strength and Point Load Strength of Rocks[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1996,33(2):183-188

[17] QUANE S L, RUSSEL J K. Rock Strength as a Metric of Welding Intensity in Pyroclastic Deposits[J]. European Journal of Mineralogy, 2003, 15(5): 855-864.

[18] AKRAM M, BAKAR M Z A. Correlation Between Uniaxial Compressive Strength and Point Load Index for Salt-range Rocks[J]. Pakistan Journal of Engineering and Applied Sciences, 2007, 1: 1-8.

[19] 王 茹, 唐春安, 王述红. 岩石点荷载试验若干问题的研究[J]. 东北大学学报,2008,29(1):130-134.

[20] SABATAKAKIS N, KOUKIS G, TSIAMBAOS G.etal. Index Properties and Strength Variation Controlled by Microstructure for Sedimentary Rocks[J]. Engineering Geology, 2009, 97: 80-90.

[21] SINGH T N, KAINTHOLA A, VENKATESH A. Correlation Between Point Load Index and Uniaxial Compressive Strength for Different Rock Types[J]. Rock Mechanics and Rock Engineering, 2012, 45(2): 259-264.

[22] LI D, WONG L N Y. Point Load Test on Meta-Sedimentary Rocks and Correlation to UCS and BTS[J]. Rock Mechanics and Rock Engineering, 2013,46(4):889-896.

[23] CARGILL J S, SHAKOOR A. Evaluation of Empirical Methods for Measuring the Uniaxial Compressive Strength[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts,1990, 27(6): 495-503.

[24] GRASSO P, XU S, MAHTAB A. Problems and Promises of Index Testing of Rocks[J]. Rock Mechanics,1992,33:879-88.

[25] ULUSAY R, TURELI K, IDER M H. Prediction of Engineering Properties of a Selected Litharenite Sandstone from Its Petrographic Characteristics Using Correlation and Multivariate Statistical Techniques[J]. Engineering Geology, 1994,38(1/2):135-157.

[26] KAHRAMAN S. Evaluation of Simple Methods for Assessing the Uniaxial Compressive Strength of Rock[J]. International Journal of Rock Mechanics and Mining Sciences, doi: 10.1016/S1365-1609(01)00039-9.

[27] BASU A, KAMRAN M. Point Load Test on Schistose Rocks and Its Applicability in Predicting Uniaxial Compressive Strength[J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 47(5): 823-828.

[28] HEIDARI M,KHANLARI G,TORABI-KAVEH M,etal. Predicting the Uniaxial Compressive and Tensile Strengths of Gypsum Rock by Point Load Testing[J]. Rock Mechanics and Rock Engineering, 2012, 45(2): 265-273.

[29] 付志亮, 王 亮. 煤层顶底板岩石点荷载强度与拉压强度对比试验研究[J]. 岩石力学与工程学报,2013, 32(1): 88-97.

[30] KAHRAMAN S. The Determination of Uniaxial Compressive Strength from Point Load Strength for Pyroclastic Rocks[J]. Engineering Geology,2014,170(1):33-42.

[31] 李安平, 刘洋树, 周 明, 等. 岩石点荷载强度与单轴抗压强度关系研究[J]. 有色金属,2014,66(3):53-59.

[32] TSIAMBAOS G, SABATAKAKIS N. Considerations on Strength of Intact Sedimentary Rocks[J]. Engineering Geology, 2004,72(3/4): 261-273.

[33] SANTI P M. Field Methods for Characterizing Weak Rock for Engineering[J].Environmental & Engineering Geoscience, 2006, 12(1): 1-11.

[34] KILIC A, TEYMEN A. Determination of Mechanical Properties of Rocks Using Simple Methods[J]. Bulletin of Engineering Geology and the Environment, 2008, 67(2): 237-244.

[35] 张建明，唐志成，刘泉声. 点荷载强度指数估算与岩浆岩的单轴抗压强度的关系[J].岩土力学,2015,36(2):595-600.

[36] 郭曼丽. 试论岩石点荷载试验的适用性[J].岩土力学,2003,24(3):488-492.

[37] 郑达辉,王连俊，蔡铁仪，等.岩石点荷载强度的研究[C]∥全国第三次工程地质大会论文选集. 成都：成都科技大学出版社，1988：1075-1083.

[38] FRANKLIN J A. 测定岩石点荷载强度的建议方法[J].向桂馥,译.岩石力学与工程学报,1986,5(1):79-90.

[39] 王祥厚, 李明勇, 佘洛斐, 等. 点荷载测定岩石强度使用不规则试件研究与探讨[J].岩土力学,1995,12(4):46-56.

[40] 赵 奎, 金解放, 赵 康, 等.用岩石点荷载强度指标确定其单轴抗压强度的试验研究[J].矿业研究与开发,2005, (6):32-33, 88.

[41] 王 赢, 孙成科, 张喜平, 等. 点荷载试验在岩基评价中的应用[J].港工技术,2013,(6):56-60.

[42] 张国锋, 刘志双, 陈显坤, 等. 点荷载法测试易风化泥质岩强度的可靠性分析[J].岩土力学,2014,35(增1):292-299.

[43] 戴洪军, 蔡升华, 郭纪中.点荷载强度试验中经验公式的分析[J].工程勘察,2001,(2): 43-47.

[44] 杨 虎, 钟 波, 刘琼荪. 应用数理统计[M]. 北京:清华大学出版社,2006.

[45] 杨 帆, 谢永利. 点荷载试验确定岩石强度指标的效果分析[J]. 广西大学学报(自然科学版),2013,38(1):138-144.

[46] 曾伟雄, 林国赞. 岩石单轴饱和抗压强度的点荷载试验方法设计与探讨[J]. 岩石力学与工程学报,2003,22(4): 566-568.