基于无功补偿的电气弹簧稳压及谐波抑制的双闭环控制

王辉航， 赵朝会， 詹 俊

(上海电机学院 电气学院, 上海 201306)

新能源发电已越来越成为各国研究的热点[1-3]。为解决新能源并网导致的一系列问题[4]，研究人员提出各种治理方案：① 电池储能方法，在用电低谷期将电能用电池存储起来，在用电高峰期再将电能释放出来使用[5]。② 实时电价方法，在不同时段采用不同电价来调节用户的用电量[6]；③ 电力负荷控制方法，即直接控制是否对用户供电[7-8]。显然，上述方法的缺点显而易见，第①种方法的成本太高，第②种方法并不能有效解决问题，第③种方法会引起用户不满；这些方法都是为了满足用户用电量能与电厂发电量相当而提出的。为有效解决上述问题，文献[9]中提出了电气弹簧(Electric Spring，ES)。利用ES将电网电压的波动转移至非关键负载，以保证电网电压保持在额定值。ES和非关键负载组成的智能负载[9]对电网的8种补偿模式[10]改变了智能负载的消耗功率，使电网供需平衡，进而保证了电网电压与频率的稳定。与传统解决方案不同的是，ES实现了发电侧决定需求侧的运行模式，即发多少电，需求侧用多少电。研究人员研究了各种ES需求侧管理的控制方法。文献[11-12]中的控制方法虽能使母线电压的有效值稳定在额定值，但没有对谐波进行处理，谐波含量较大。文献[13]中虽然对母线电压的有效值进行了控制，并处理了谐波，但是，由于存在谐振控制器，使得在模拟电路中的硬件部分难以实现，不仅在数字电路中增加了计算量，且不易控制谐振控制器输出的谐波。文献[14]中通过对电路参数的计算，得出关键负载母线电压与发电侧电压的相角差，实现控制关键负载电压准确地跟踪给定正弦波。该方法受电路参数的影响，且数字控制器的计算量较大。

本文针对ES母线电压不稳定及谐波问题，对母线电压有效值的控制和减少母线电压的谐波进行了研究。分析了ES的工作原理，为ES的控制提供依据；利用单闭环母线电压有效值控制方案进行母线电压控制，并在此基础上加入谐波控制环，形成双闭环控制，同时实现了母线电压有效值控制和谐波抑制的功能。仿真实验验证了该方法的可行性。

1 ES结构及工作原理分析

1.1 ES的结构

ES由功率变换器、直流侧电源和LC低通滤波器构成。ES和非关键负载Znc串联形成智能负载，并与关键负载Zc并联接入电网。

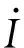
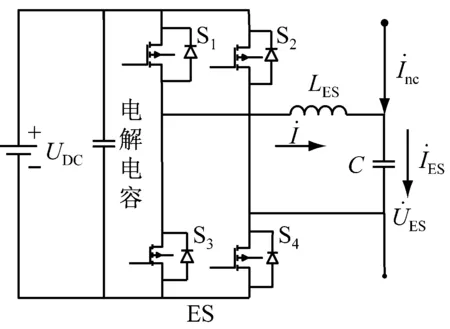
(a) ES结构图

图1ES结构图和其在电网中的连接图

在图1(b)中，

ZL=RL+jXL

(1)

式中：RL为线路电阻;XL=ωLL为线路电抗；ω为电网角频率；LL为线路电感。

关键负载为

Zc=Rc+jXc

(2)

式中：Rc为关键负载上的电阻；Xc=ωLc为关键负载上的电抗；Lc为关键负载电感。

非关键负载为

Znc=Rnc+jXnc

(3)

式中：Rnc为非关键负载上的电阻；Xnc=ωLnc为非关键负载上的电抗；Lnc为非关键负载上的电感。

1.2 ES工作原理分析

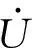
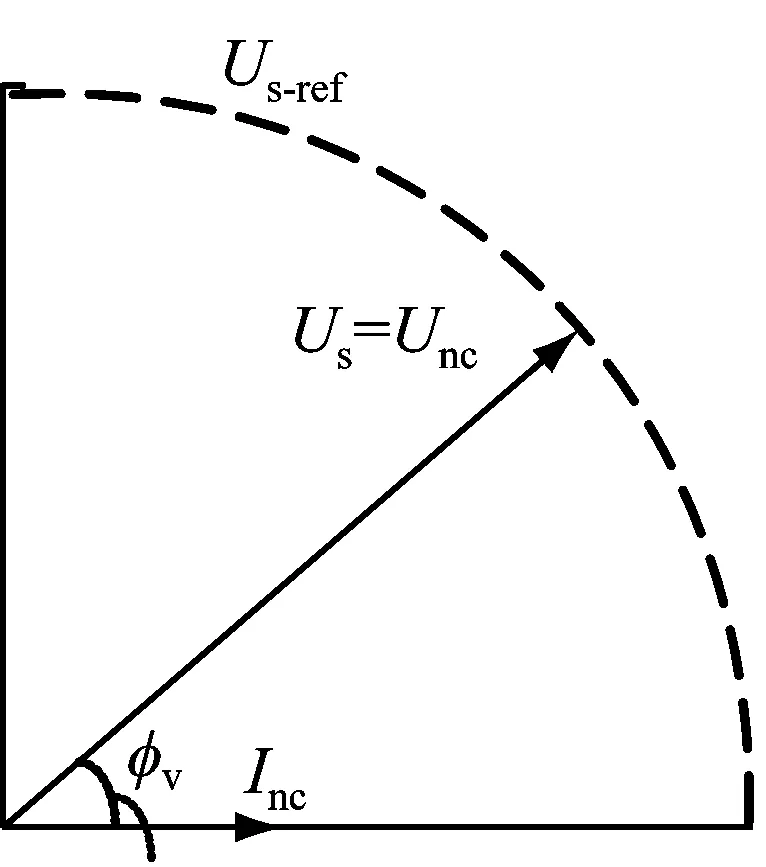
(a) 阻性模式

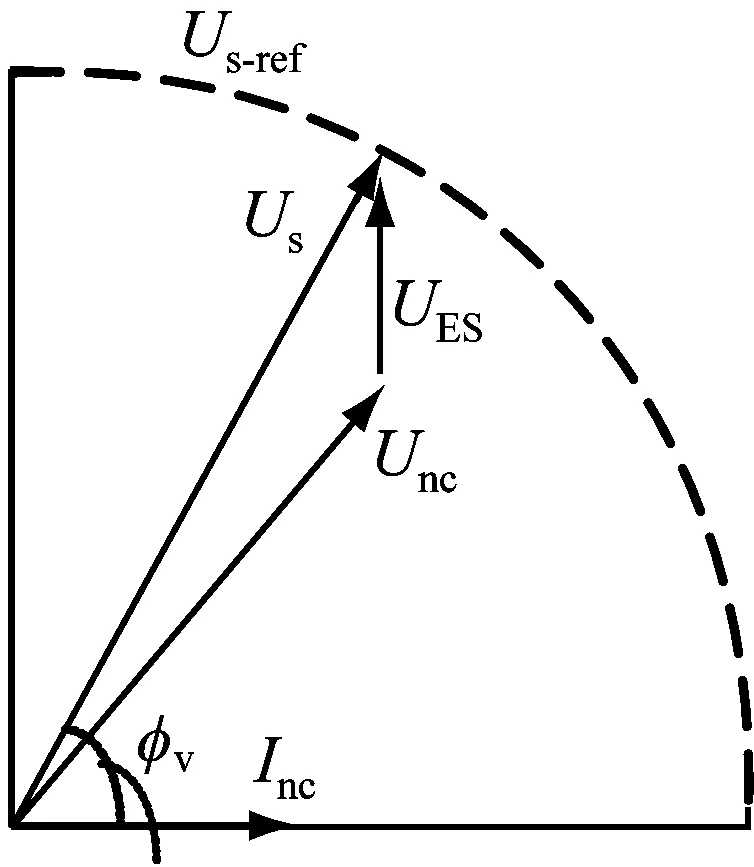
(b) 容性模式

(c) 感性模式

图2ES的工作模式

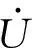
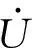
由图1(b)，有

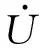
(4)

在节点a处运用基尔霍夫电流定律(KCL)可得

(5)

结合图2(b)，有

由式(6)可得

(9)

由式(4)、(5)、(7)可得

(10)

由式(8)～10)可得

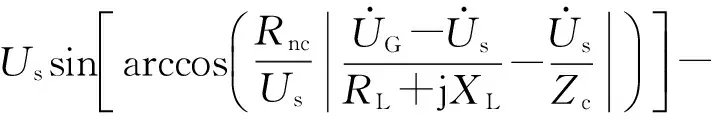
(11)

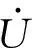
2 ES控制原理分析

文献[11]对ES的控制只能将母线电压的有效值控制在额定值，缺少对其谐波的处理，因此，谐波含量较多。本文将这种只控制母线电压有效值的方法称为单闭环母线电压有效值控制，并在其基础上，加入谐波抑制环节，达到对母线电压有效值控制和谐波抑制的双重功效，故称为双闭环控制。

2.1 单闭环母线电压有效值控制

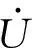
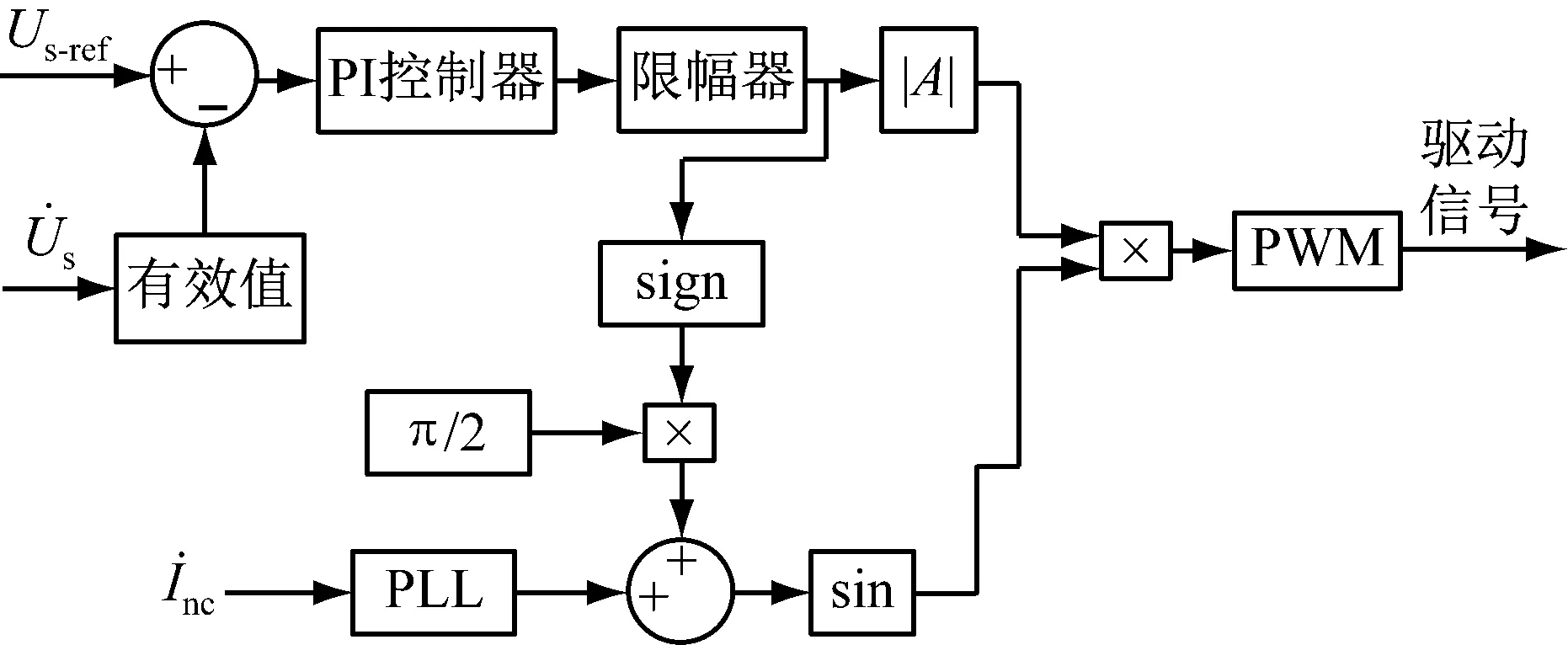
图3 单闭环母线电压有效值控制框图

2.2 双闭环控制

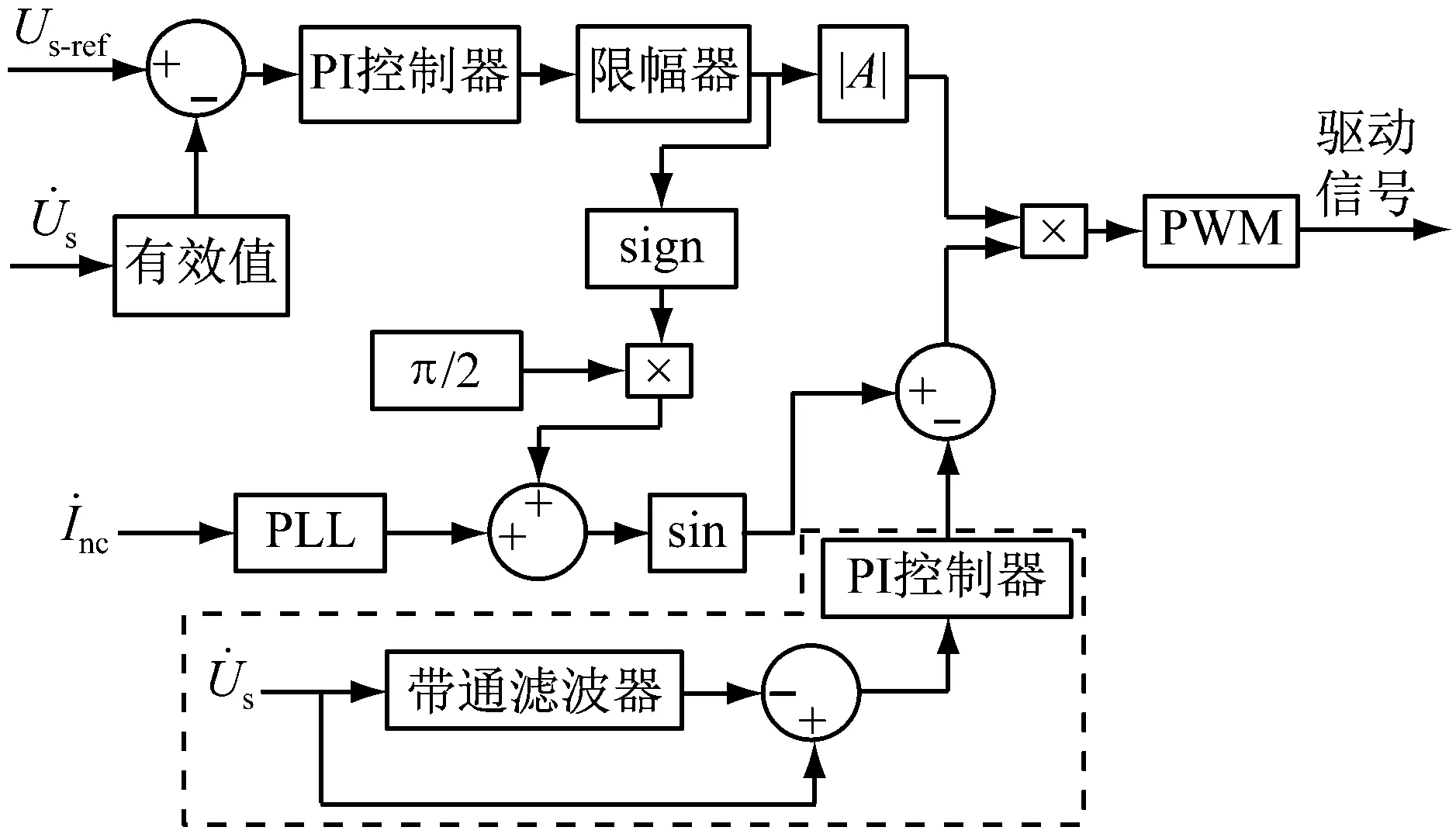
图4 双闭环控制框图

要使图4中谐波控制环节取得较好的谐波控制效果，关键在于带通滤波器中传递函数的选取。实际工作中，由于能让工频信号无损通过，而其他频率信号通过时能无限衰减的理想的带通滤波器是不存在，因此，带通滤波器的选择原则如下：应使工频信号尽量无损通过，而其他频率信号通过时最大限度地衰减；且带通滤波器为二阶传递函数，以使模拟电路中的硬件部分较容易实现。因此，本文中选择带通滤波器中的s域传递函数为

(12)

式中：ω为工频信号的角频率，ω=2πf=2π×50=100 π，其中，f=50 Hz为工频；λ为系数,选取不同的λ值，幅频特性也不同。图5所示为λ取不同值时，带通滤波器传递函数的幅频特性图。

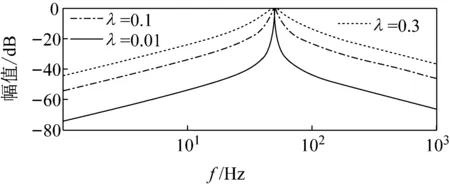
图5 带通滤波器传递函数的幅频特性图

由图5可见，无论λ取何值，只有当f=50 Hz(工频)时，信号才能无损通过，而其他频率信号都有不同程度地衰减，且λ越小，衰减幅值越大。虽然理论上λ值越小越好，但是，由于实际工作中，若λ太小，则带通滤波器中的通频带越窄，工频信号稍有点偏差，就会引起较大误差。经过多次实验，本文取λ=0.01。

3 ES模型搭建与仿真分析

为验证上述分析的可行性，在Matlab/Simulink软件中按照图1(b)搭建ES在电网中的连接模型,同时，设UG=190 V,RL=0.2 Ω，LL=23 mH,Znc=Zc=50 Ω,UDC=500 V,LES=1 mH,C=75 mF。

根据图3和图4分别搭建单闭环母线电压有效值控制和双闭环控制的仿真模型，图6所示为双闭环控制仿真模型。设置仿真时间为2 s，分别进行2种控制方式下的仿真实验。

图7所示为仿真得到2种控制方式下的母线电压有效值波形和母线电压波形。

由图7(a)、(c)可见，2种控制方式下的母线电压有效值基本一致，都稳定在220 V左右；由图7(b)、(d)可见，2种控制方式下的电压波形的正弦化程度都较高，单闭环控制下电压峰值在310 V；双闭环控制下，电压峰值在311 V左右。说明2种控制方式对电压的控制都很稳定。

图8所示为2种控制方式下母线电压的谐波畸变率。

图6双闭环控制的仿真模型

(a) 单闭环控制母线电压有效值波形

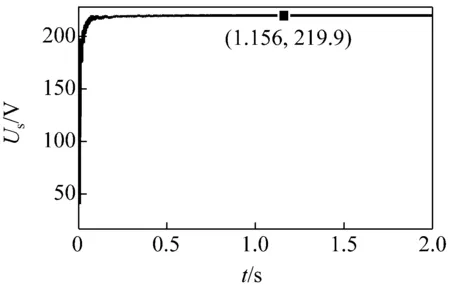
(c) 双闭环控制母线电压有效值波形

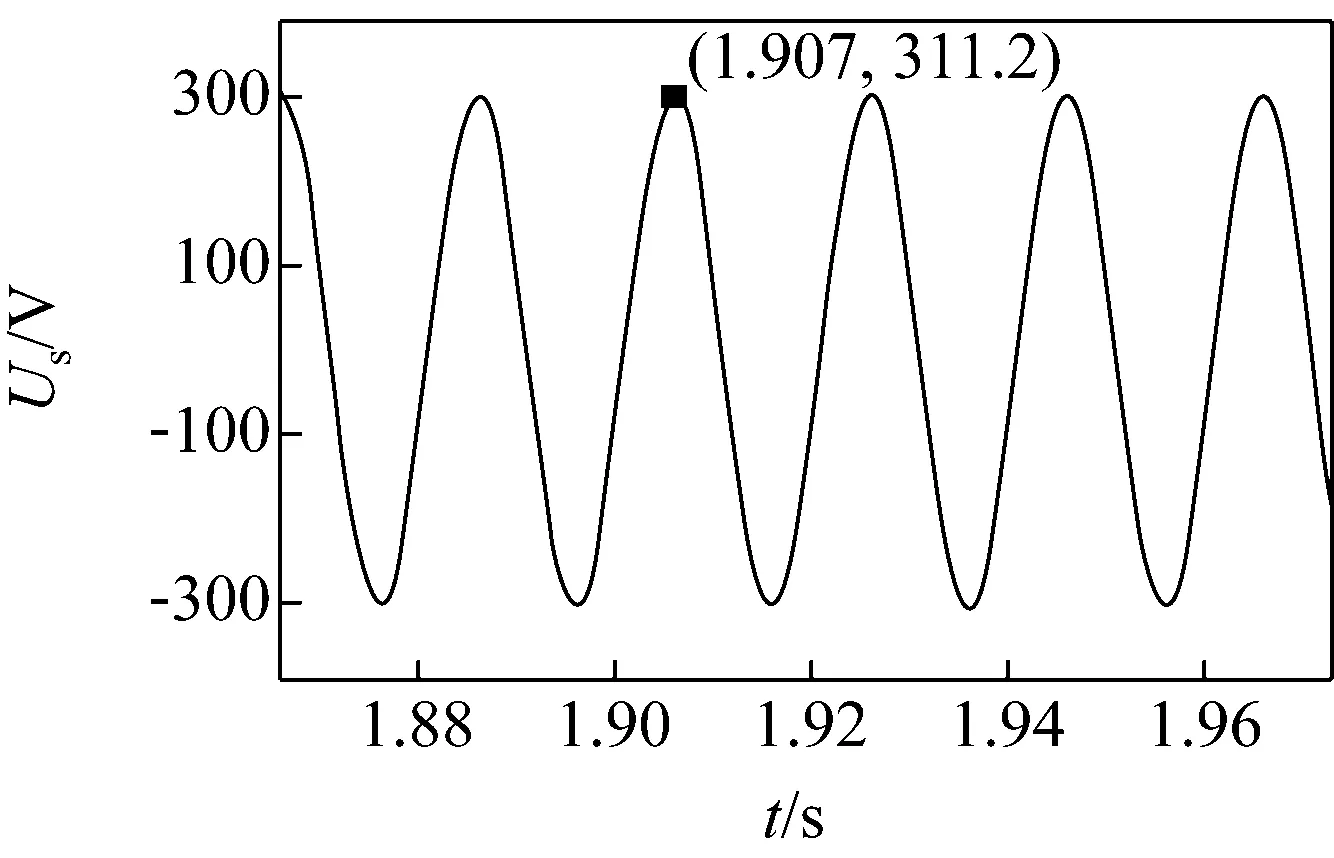
(d) 双闭环控制母线电压波形

图7单、双闭环2种控制方式下的母线电压有效值波形和母线电压波形

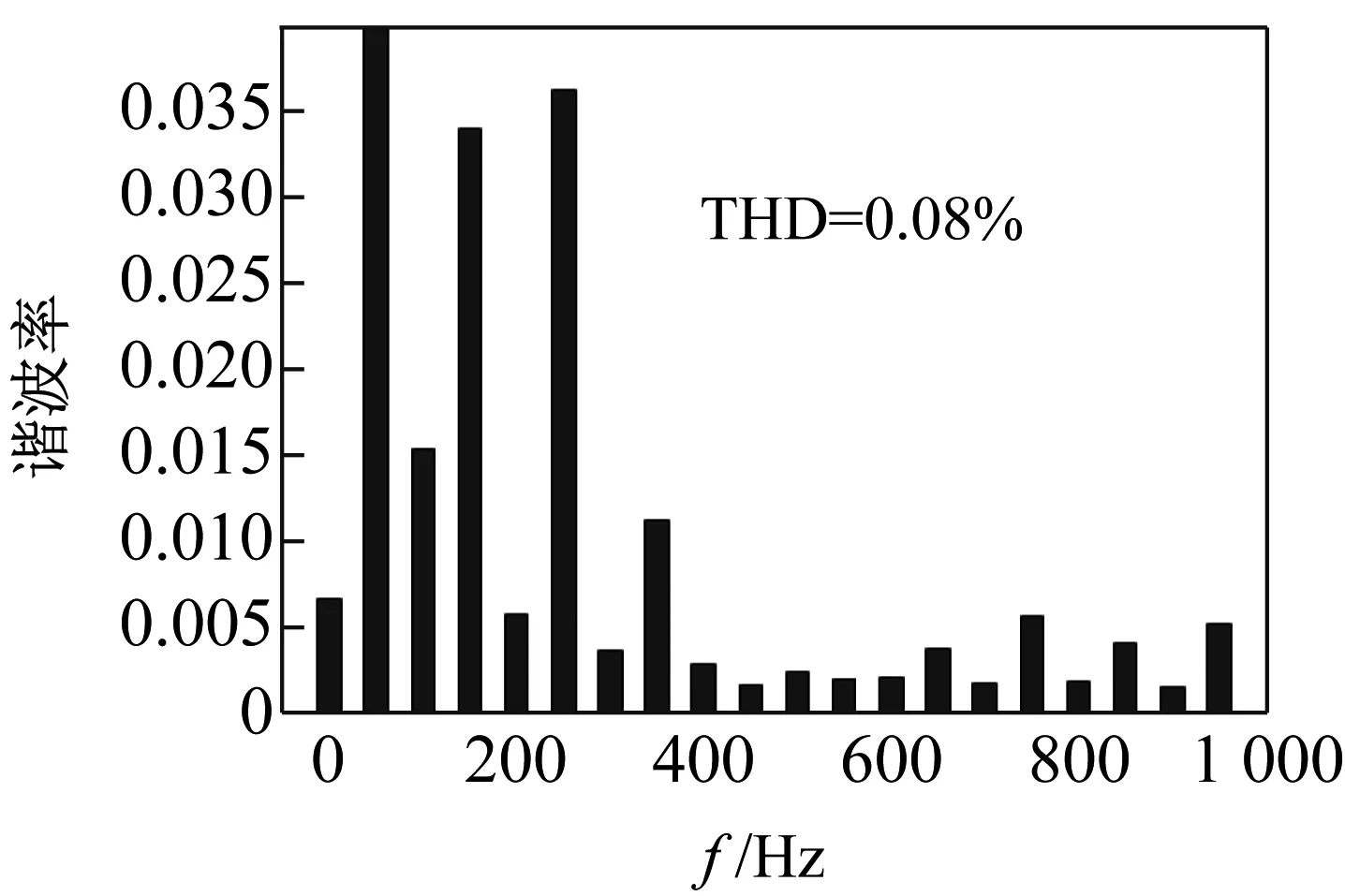
(b) 双闭环控制

由图可见，在单闭环控制下，母线电压的谐波畸变率THD=0.64%，而双闭环控制下母线电压的谐波畸变率THD=0.08%，由此可见，双闭环控制中由于加入了谐波控制环节，使谐波得到了有效抑制。

5 结 语

本文通过对ES工作在阻性、容性、感性3种模式的分析，得出了通过PI控制下的无功功率补偿来调节母线电压有效值的结论，并给出了单闭环母线电压控制方案。然后，在单闭环母线电压控制的基础上加入了谐波控制环，形成双闭环控制，同时实现了母线电压有效值控制和谐波抑制的功能。仿真结果表明，单闭环母线电压有效值控制可以实现母线电压的稳压功能，但谐波含量较多；加入了二阶滤波器谐波控制环的双闭环控制，既实现了母线电压有效值控制，又抑制了谐波，且效果良好，可见，双闭环控制具有一定的可行性。

[1] DOSHI N, LELEKAKIS N, MARTIN D， et al. A zero carbon future: Based on current initiatives, how long before Australia meets its energy needs from renewable energies? [C]// 2013 Australasian Universities Power Engineering Conference (AUPEC). Hobart, TAS, Australia: IEEE, 2013: 1-6.

[2] LORUBIO G, SCHLOSSER P. Euro mix: Current european energy developments and policy alternatives for 2030 and beyond [J]. IEEE Power and Energy Magazine, 2014,12(2):65-74.

[3] CHINA DAILY. China eye s 20% renewable energy by 2020 [N/OL]. (2009-06-10)[2017-02-25]. http://www.chinadaily.com.cn/china/2009-06/10/content_8268871.htm.

[4] 张海燕. 新能源并网对内蒙古500 kV超高压电网及500 kV变电站安全运行的影响分析 [D].北京：华北电力大学,2015:11-12.

[5] 林海雪. 现代储能技术应用概况及展望 [J]. 电源学报，2015，13(5)：34-40.

[6] CONEJO A J, MORALES J M， BARINGO L. Real-time demand response model [J]. IEEE Transactions on Smart Grid, 2010(3): 236-242.

[7] LEE S C, KIM S J, KIM S H. Demand side management with air conditioner loads based on the queuing system model [J]. IEEE Transactions on Power Systems, 2011, 26(2): 661-668.

[8] 周潮，邢文洋，李宇龙. 电力系统负荷预测方法综述 [J]. 电源学报，2012，10(6)：32-39.

[9] HUI S Y R, LEE C K, WU F. Electric springs—A new smart grid technology [J]. IEEE Transactions on Smart Grid, 2012,3(3): 1552-1561.

[10] TAN S C，LEE C K，HUI S Y R．General steady-state analysis and control principle of electric springs with active and reactive power compensations [J]．IEEE Transactions on Power Electronics，2013，28(8)：3958-3969.

[11] CHAUDHURI N R, LEE C K, CHAUDHURI B, et al. Dynamic modeling of electric springs [J]. IEEE Transactions on Smart Grid, 2014,5(5):2450-2458.

[12] LEE C K, CHAUDHURI N R, CHAUDHURI B, et al. Droop control of distributed electric springs for stabilizing future power grid [C]// 2015 IEEE Power & Energy Society General Meeting. Denver, CO, USA:IEEE,2015:1-1.

[13] KANJIYA P, KHADKIKAR V. Enhancing power quality and stability of future smart grid with intermittent renewable energy sources using electric springs [C]// 2013 International Conference on Renewable Energy Research and Applications (ICRERA). Madrid, Spain: IEEE, 2013: 918-922.

[14] 程明,王青松,张建忠. 电力弹簧理论分析与控制器设计 [J]. 中国电机工程学报,2015,35(10):2436-2444.

[15] GYUGYI L, SCHAUDER C D, WILLIAMS S L, et al. The unified power flow controller: a new approach to power transmission control [J].IEEE Transactions on Power Delivery,1995,10(2):1085-1097.

[16] AKAGI H, KANANZAWA Y, NABA A. Instantanneous reactive power compensators comprising switching devices without energy storage components [J].IEEE Transactions on Industry Applications,1984, IA-20(3):625-630.