基于改进鸡群算法的风能资源评估

吕 辉， 陈国初

(上海电机学院 电气学院，上海 201306)

对风电场风能资源进行评估是风电场建设前期的一项基础性工作[1-2]。其中，对历史测风数据资料进行概率分布研究是风能资源评估中的重点工作。目前，还没有从成因和理论上给出某地风速概率分布的形式，但是，应用最多的方法是两参数威布尔(Weibull)分布模型[3]。

对于两参数Weibull分布模型，只要确定了形状参数k和尺度参数c后，就可以计算体现风能资源特性最重要的4个特征指标，即年平均风速、年平均风能密度、年平均有效风能密度以及风能利用时间，故k和c的精度直接影响了特性指标的精度。通常，k和c参数确定的方法有最小二乘法[4]、矩估计法[5]、极大似然估计参数法[6]等；但是，这些方法有的简单、易实现，却精度差；有的精度高，却难以实现。因此，迫切需要研究一种更为有效的计算方法。

本文针对鸡群算法[7](Chicken Swarm Optimization, CSO)中，鸡妈妈在陷入局部最优时，小鸡也会陷入局部最优，且母鸡和小鸡缺少自我学习能力的问题，研究了一种改进的CSO算法，用于寻找k和c的最优值，以便能更精确地评估风能资源。最后，将改进的CSO算法应用于实际风电场的风能资源评估，并参照实测数据统计结果比较了利用改进的CSO算法与等能量密度法进行风能资源评估的精度。

1 改进的CSO算法

1.1 基本CSO算法

CSO算法是由MENG等[8]于2014年提出的一种基于鸡群搜索行为的随机优化方法，它模拟了鸡群等级制度和鸡群行为。将整个鸡群分为若干子群，每个子群都由1个公鸡、若干母鸡和小鸡组成。不同的鸡遵循不同的移动规律，在具体的等级制度下，不同的鸡群之间存在竞争，因此，CSO算法是一种全局优化算法。

假设整个鸡群中NR个公鸡、NH个母鸡、NC个小鸡、NM个鸡妈妈，个体位置xij(t)表示第i个体的j维在第t次迭代的值，则公鸡对应的位置更新为[9]

xR_i,j(t+1)=xR_i,j(t)[(1+Randn(0,σ2)]

(1)

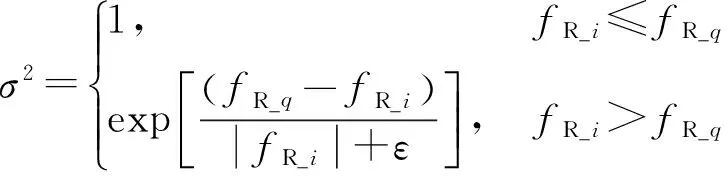
(2)

q∈[1,NR]，q≠i

(3)

式中:Randn(0,σ2)为均值为0、标准差为σ2的一个高斯分布；ε为一个很小的常数；q为所有公鸡中除去i外的任一个体；fR_i和fR_q分别为公鸡i，q的适应度值。

母鸡的位置更新为:

xH_i,j(t+1)=xH_i,j(t)+C1Rand·(xH_r1,j(t)-

xH_i,j(t))+C2Rand·(xr2,j(t)-

xH_i,j(t)),r1≠r2

(4)

C1=exp((fH_i-fH_r1)/(abs(fH_i)+ε))

(5)

C2=exp[(fr2-fH_i)]

(6)

式中:Rand为[0，1]中的随机数；xH_r1,j(t)为该母鸡所属族群公鸡的位置信息；xr2,j(t)为其他族群公鸡的位置信息；C1和C2分别为母鸡参考自身族群和其他族群搜索的权重；fH_i和fH_r1分别为母鸡i和所属族群公鸡r1的适应度值；fr2为其他族群公鸡r2的适应度值，r1≠r2。

由式(3)可见，母鸡的位置更新由3部分构成：上一次迭代母鸡所处的位置；与所属族群公鸡的位置关系；与其他族群公鸡的位置关系。这模拟了自然界中母鸡既跟随自身族群搜索食物，又从其他族群偷取食物的机制。由式(5)和式(6)可知，C1>1>C2，故母鸡的位置将更多地参考自身族群公鸡所处位置。

小鸡的位置更新为

xC_i,j(t+1)=xC_i,j(t)+F·

(xC_m,j(t)-xC_i,j(t))

(7)

式中:m为第i只小鸡对应的母鸡；F(F∈[0,2])为跟随系数，表示小鸡跟随母鸡寻找食物的紧密度。

1.2 改进CSO算法的主要改进措施

1.2.1 增强小鸡向公鸡学习的能力 在CSO算法中，小鸡只向鸡妈妈学习，并没有向自身所在群中的公鸡学习，这就很容易导致当鸡妈妈陷入局部最优时，小鸡也因此陷入局部最优，从而导致整个鸡群算法陷于局部最优，影响算法的精度。本文在小鸡更新自己的位置时，不仅获取鸡妈妈的位置信息，还要获得整个子群中公鸡的位置。通过实验仿真，在控制其他变量不变的情况下，改变学习因子C的值(C∈(0，1))，即每隔0.1改变一次，找出最为合适的C值。

1.2.2 增强母鸡、小鸡自我学习能力 在基本CSO算法中，母鸡、小鸡都没有自我学习能力，这降低了算法的寻优能力，本文引进自我学习系数ω(与粒子群的惯性权值类似)。传统的惯性权值的线性、非线性动态调整主要是在迭代初期，将惯性权值设为较大值，使其具有较强地探索能力，有利于全局搜索；而在迭代后期，将惯性权值设为较小值，使其进行更为精细的局部搜索，以便得到更精确的解。但这些方法的惯性权值调节方法太过单一，微粒均采用相同的惯性权值，忽略了微粒的独特性，降低了种群的多样性，遇到复杂函数(多峰、高维)时，很难跳出局部最优值。为此，本文使ω随着各自的适应度值自适应调节。以极小值问题为例，自我学习系数设置如下[10-11]：

ω=

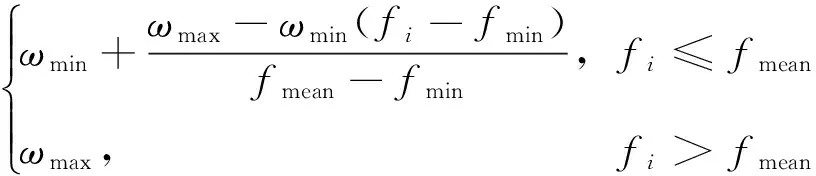
(8)

式中:ωmin和ωmax分别为最小、最大自我学习系数；fmean为平均适应度值；fmin为最小适应度值；fi为整个鸡群每次迭代的适应度值。

因此，改进后的母鸡位置更新为

xH_i,j(t+1)=ωxH_i,j(t)+C1Rand·

(xH_r1,j(t)-xH_i,j(t))+C2Rand·

(xr2,j(t)-xH_i,j(t))

(9)

改进后的小鸡位置更新为

xC_i,j(t+1)=xC_i,j(t)+ωF·(xC_m,j(t)-

xC_i,j(t))+C(xr,j(t)-xC_i,j(t))

(10)

1.3 改进的CSO算法流程

(1) 初始化鸡群位置信息x，并定义相关参数NR，NH，NC，NM等；

(2) 计算鸡群的适应度值fi，初始化个体当前最好位置pb和鸡群全局最好位置gb，t=1；

(3) 若t%G=1或t=1(G为排序间隔长度)，则对fi排序，建立鸡群等级制度，将鸡群分成数个子群，并确定母鸡和小鸡的对应关系；

(4) 利用式(1)、(9)和(10)分别更新公鸡、母鸡和小鸡的位置，计算每个个体的适应度值；

(5) 更新鸡群个体当前的最好位置和鸡群全局的最好位置。

(6) 令t′=t+1，若满足迭代停止条件，则停止迭代，输出最优值；否则，转到步骤(3)。

2 改进的CSO算法性能

为了考察改进后CSO算法的性能，本文利用3个经典测试函数对其进行仿真实验，并对结果加以分析。3个测试函数中，Schaffer和Rosenbrock函数为单模函数，用于考察算法的寻优精度和收敛速度；Griewank函数为多模函数，用于考察算法摆脱局部最优解和全局搜寻的能力。

(1) Schaffer函数

x1,x2∈[-10，10]

(2) Griewank函数

-600≤xi≤600

(3) Rosenbrock函数

x1,x2∈[-2.048，2.048]

上述3个测试函数的共同点是全局最小值为零，且很难找到全局最优值。Schaffer函数是二维函数，在(0,0)处取得最小值0；Griewank函数是非线性多模态函数，在(x1,x2,…，xn)=(0,0,…，0)处取得全局最小值0；Rosenbrock函数在二维情况下，在(1,1)可取得唯一全局最小值为零。

利用CSO算法和本文改进的CSO算法对测试函数进行仿真实验，实验所用软件为Matlab R2014a，实验参数设置如下：群体数量为100，最大迭代数为1 000，G=10，C=0.3，ωmax=1.5，ωmin=0.04；为得到客观评价，结果均是在进行了100次独立测试后取其均值后得到。表1所示为维数为2时，CSO算法和改进的CSO算法对测试函数的求解结果。由表可见，改进的CSO算法的寻优能力明显好于CSO算法，这是由于改进的CSO算法中引进了C和ω；从搜索时间看，虽然改进的CSO算法比CSO算法稍微慢了一些，这是由于改进的CSO算法结构较CSO复杂，但从权衡看，改进的CSO算法用少量的时间换取了高精度，是可取并有意义的。

3 两参数Weibull模型风能评估建模

两参数Weibull分布模型的分布函数为[12]

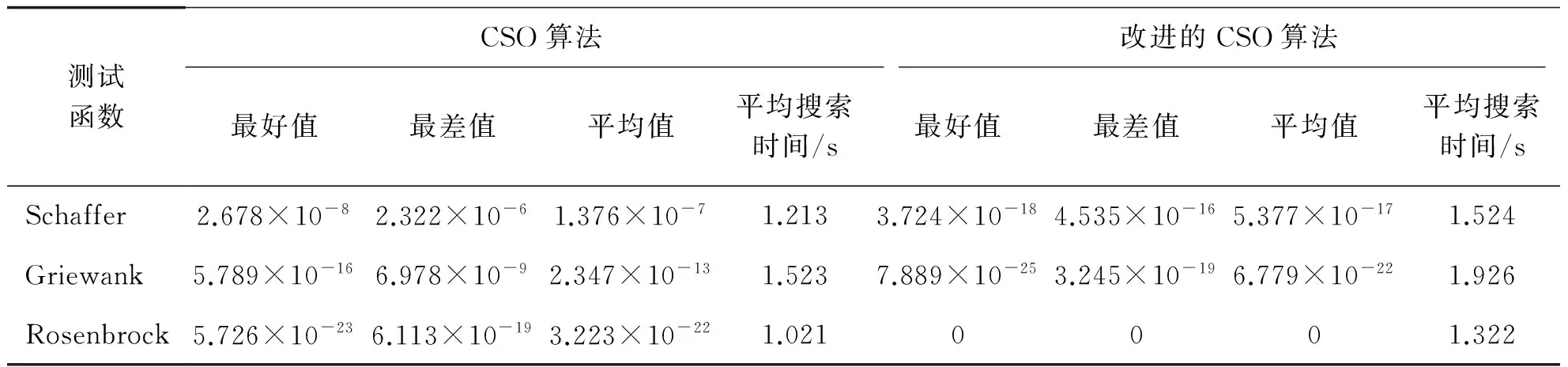
表1 维数为2时，CSO和改进的CSO算法对测试函数的求解结果

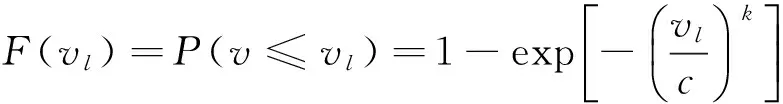
(11)

其概率密度函数为[13]

(12)

式中:v为实际测量风速；vl为第l个风速值；P(v≤vl)为实际测量风速小于第l个风速值的概率。

3.1 等能量密度法建模

等能量密度法是WAsP软件中用来进行风能资源评估的方法，在工程实际中被广泛应用。此方法的中心思想是确保最大限度地表达风的能量部分。利用等能量密度法估计Weibull分布的2个参数需要满足以下条件[14-15]：① 风能密度相等；② 大于平均风速的风频概率相同。

根据实测风速数据统计出风速大于年平均风速的概率，记为X，则可得到

(13)

设k的初值为2，经过多次迭代计算，稳定后的解即为k的解。则可计算得到

(14)

式中:v测为实测的平均风速。

3.2 改进的CSO算法优化Weibull分布模型建模

建立如下的风速Weibull分布模型参数的目标优化函数：

(15)

式中:E(k,c)为误差平方和函数，当其为极小值时，对应的k,c即为所要计算的最优解(k,c)；Pvl为实际第l个风速值vl(即vl=1 m/s)的统计概率；N为原始风速数据划分的风速段数。

利用改进的CSO算法优化Weibull分布模型参数的流程如图1所示。

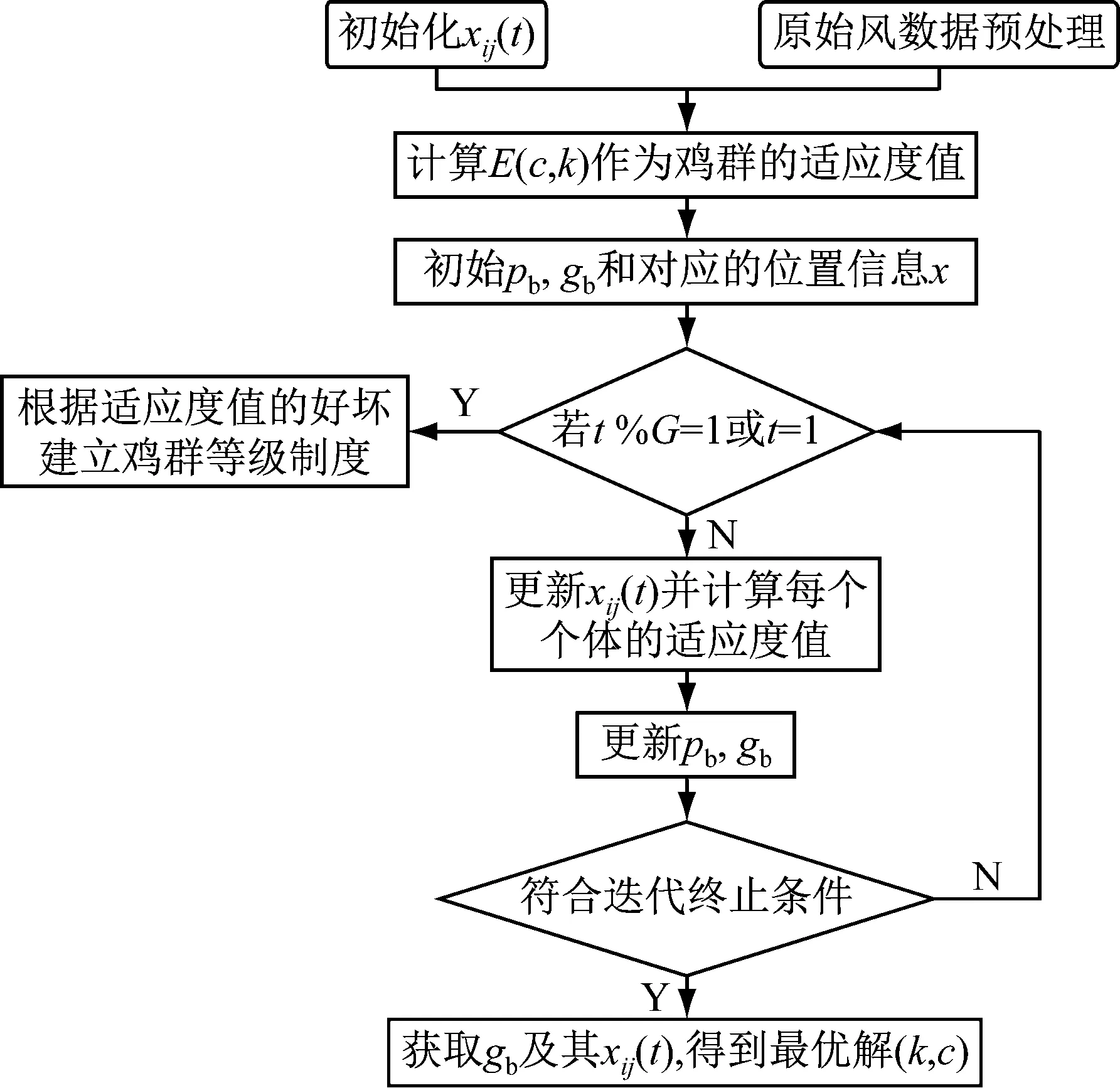
图1 优化的Weibull分布模型参数流程图

4 实例与结果分析

4.1 背景介绍

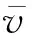
表2 不同轮毂高度实际测量得到的风能资源特性指标值

4.2 风能特性指标统计结果及分析

利用等能量密度法和改进的CSO算法分别计算k,c，然后，利用计算得到的结果分别对实测风速数据进行风能资源评估，即计算风能资源的特性指标值，得到的结果如表3所示。

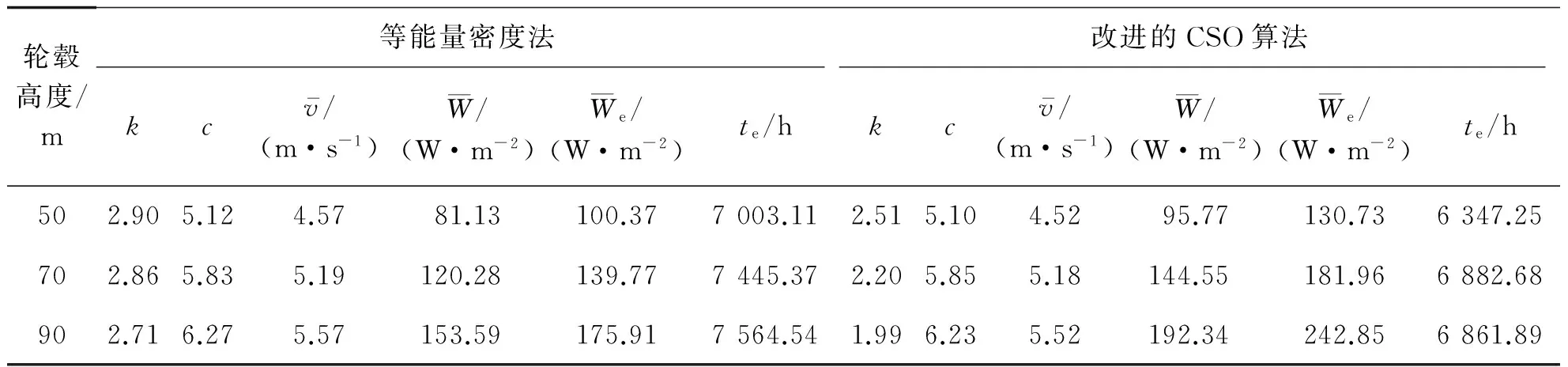
表3 2种方法计算得到的k,c及风能特性指标评估值

为评价改进的CSO算法对风能资源特性指标的评估精度，利用绝对误差e和相对误差R对评估结果进行评价，并与等能量密度法进行比较，其中:

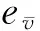
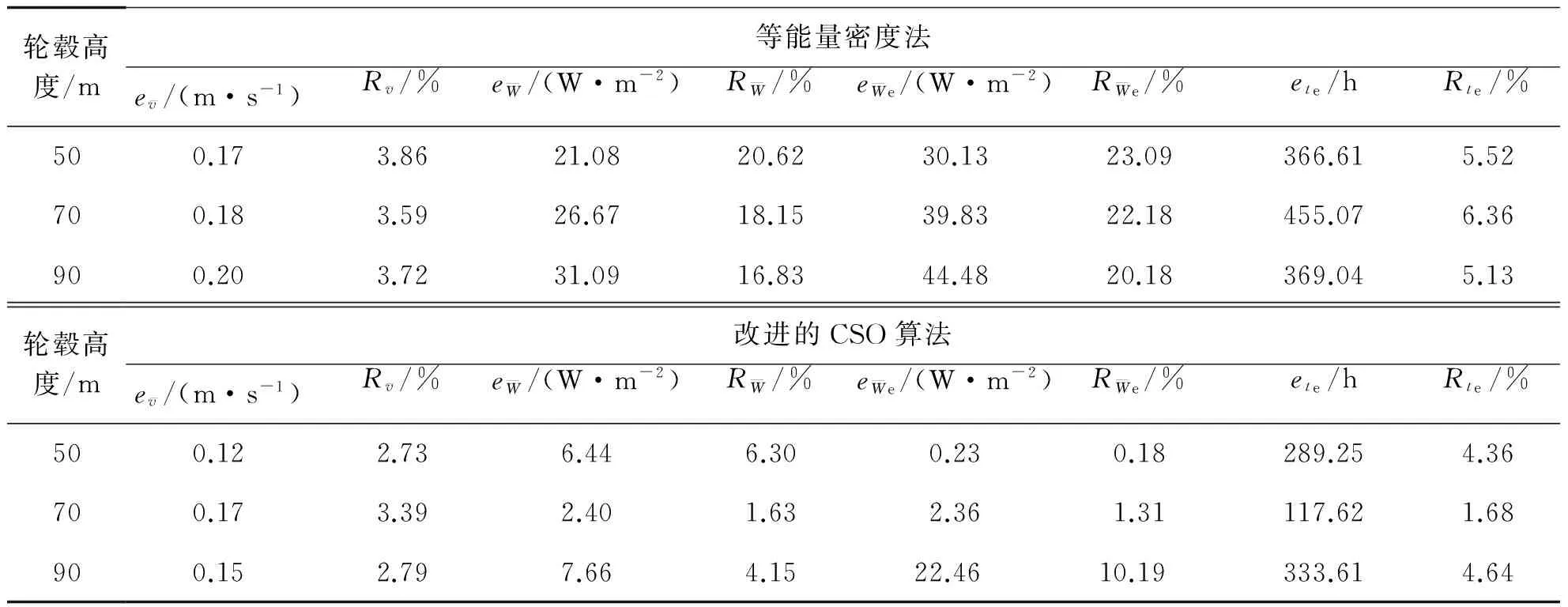
表4 2种方法在不同轮毂高度的风能资源特性指标评价结果

5 结 语

考虑到风速分布服从两参数Weibull分布函数，本文在CSO算法的基础上，引入小鸡的学习因子C和自我学习系数ω加以改进，并利用河南开封尉氏某风电场连续一年的的测风数据对改进的鸡群算法进行验证。结果表明，利用改进的CSO算法寻优得到的Weibull参数所计算出的风能特性指标误差率普遍较好，由此可见，改进的CSO算法更适合应用于风电场的风能资源评估。

[1] 封宇, 何焱, 朱启昊,等. 近海及海上风资源时空特性研究 [J]. 清华大学学报(自然科学版), 2016，56(5)：522-529.

[2] 郁永静, 何一, 刘志远，等. 基于最大熵原理的风电场风频分布研究 [J]. 水力发电, 2017，43(6)：93-96，119.

[3] 陈国初,杨维,张延迟,等.风电场风速概率分布参数计算新方法[J].电力系统及其自动化学报,2011,23(01):46-51.

[4] 陈光，任志良，孙海柱.最小二乘曲线拟合及Matlab 实现 [J].兵工自动化，2005，24(3)：107-108.

[5] BAUM C F，SCHAFFER M E，STILLMAN S. Enhanced routines for instrumental variables/generalized method of moments estimation and testing [J]. Boston College Working Papers in Economics, 2007，7(4):465-506.

[6] METZ C E, HERMAN B A, SHEN J H. Maxi-mum likelihood estimation of receiver operating characteristic (ROC) curves from continuously-distributed data [J]. Statistics in Medicine，2015，17(9):1033-1053.

[7] QU Chiwen, ZHAO Shi’an, FU Yanming，et al. Chicken Swarm Optimization Based on Elite Opposition-Based Learning [J]. Mathematical Problems in Engineering，2017，2017：1-20.

[8] Meng X, Liu Y, Gao X, et al. A new bio-inspired algorithm: Chicken swarm optimization[G]// Advances in Swarm Intelligence.[S.l.]: Springer International Publishing, 2014: 86-94.

[9] 孔飞, 吴定会. 一种改进的鸡群算法 [J]. 江南大学学报(自然科学版), 2015, 14(6):681-688.

[10] 叶林, 杨丹萍, 赵永宁. 风电场风能资源评估的测量—关联—预测方法综述 [J]. 电力系统自动化, 2016,40(3):140-151.

[11] 杨维, 陈国初, 张延迟,等. 改进的微粒群算法及其在风电场建模中的应用 [J]. 计算机工程与应用, 2011, 47(1):223-227.

[12] LI Gong, SHI Jing. Application of Bayesian model averaging in modeling long-term wind speed distributions [J]. Renewable Energy, 2010, 35(6):1192-1202.

[13] CARTA J A, RAMíREZ P. Analysis of two-component mixture Weibull statistics for estimation of wind speed distributions [J]. Renewable Energy, 2007, 32(3):518-531.

[14] WANG Zhifeng， DONG Sheng， DONG Xiangke，et al. Assessment of wind energy and wave energy resources in Weifang sea area [J]. International Journal of Hydrogen Energy, 2016, 41(35):15805-15811.

[15] MAHMUDDIN F, IDRUS M, HAMZAH. Analysis of ocean wind energy density around sulawesi and maluku islands with scatterometer data [J]. Energy Procedia, 2015, 65:107-115.