基于快速匹配追踪的混合域地震稀疏反演方法

李 坤, 印兴耀, 宗兆云, 彪芳书

(1.中国石油大学地球科学与技术学院,山东青岛 266580;2.海洋国家实验室海洋矿产资源评价与探测技术功能实验室,山东青岛 266580)

由于地震数据频带特征表现为带限支撑,地层反射系数稀疏性假设作为重要先验信息约束,可以缓解反演算法的不稳定性和多解性。针对稀疏性先验约束方面,目前主要存在正则化方法和经典贝叶斯估计框架[1-3]。贝叶斯模型先验概率密度信息旨在压制弱小反射突出非弱小反射系数序列,其预测的地层弹性参数并非为绝对稀疏序列[4-8],而稀疏正则化手段则可有效获取绝对稀疏的模型参数[2-3],稀疏反射序列突出地层边界变化,相比连续变化预测结果具有更高的频带宽度和分辨能力[9]。匹配追踪算法在地震资料处理和解释领域得到广泛应用,如非平稳信号时频分解[10-15]、地震数据规则化和插值[16-19]、高分辨率反射率反演[20-22]、强反射屏蔽去除[23-26]、地震去噪[27]及偏移成像处理等[28-29]。Mallat等[12]采用Gabor函数构建超完备冗余字典,率先将任意信号表示为最优原子的线性组合。Özbek等[16]利用匹配追踪地震信号自适应分解的思想,提出不规则采样地震数据的正则化和迭代插值技术。Nguyen等[9]将贪婪匹配追踪算法引入地震高分辨率反射系数反演中,相比于常规最小二乘反演方法有更高的抗噪能力。Li等[15]结合匹配追踪谱分解算法和叠前AVO(amplitude variation with offsets，振幅随着偏移距变化)直接反演理论,提出了高分辨率频变AVO(F-AVO, frequency dependent AVO)流体检测方法。Wen等[20]将奇偶反射系数分解策略引进贪婪匹配追踪反射系数反演中,发展了相对纵波阻抗的块化估计技术。然而,经典匹配追踪反演在每次迭代过程中仅恢复单一反射系数,存在计算效率低和收敛速度慢的问题。笔者借鉴快速匹配追踪算法的思想,提出基于多原子快速匹配追踪的混合域地震稀疏反演方法,通过将Margrave混合域褶积[30]和纵波阻抗低频约束相结合,构建混合域稀疏正则化目标泛函。

1 基于快速匹配追踪的混合域地震反演原理

1.1 混合域地震反演原理

Margrave等[30]在考虑地震波受到地下介质固有Q值衰减效应时,推导了平稳地震褶积模型的时间域、频率域以及混合域等表达形式。为了更好地约束地震反演中待反演模型参数且获得高分辨率反演结果[1,9,31],本文中采用平稳地震混合域褶积模型作为正演方程:

(1)

式中,f为频率;S(f)为实际地震频谱响应;W(f)表示地震子波的频率域形式;r(t)为地层界面时间域反射系数;No(f)为随机噪声频谱。将式(1)中地震频谱S(f)和反射系数r(τ)的关系利用映射核矩阵表示:

(2)

式中,fk为选取的部分频率成分;S为输入地震频谱;W为地震子波频谱。式(1)中待反演模型参数(映射前向量)R和傅里叶算子C可表示为

(3)

式中,r(τM)为地下介质M个反射系数。联合式(2)和式(3)且令映射核矩阵G=WC,则式(1)中平稳褶积混合域表达式可表示为

S=GR+No.

(4)

式中,No为地震随机噪音向量。由于方程(4)为混合域复数方程组,将其展开为实部和虚部形式:

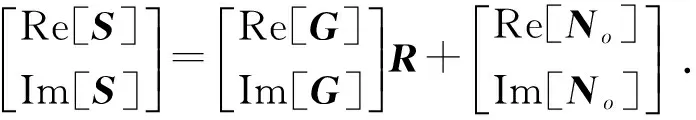
(5)

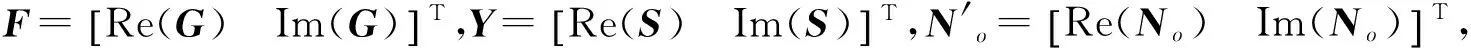
(6)

利用L2范数描述理论数据FR与实际数据Y之间的拟合程度,则最小二乘目标泛函Js(R)可表述为

(7)

式(7)旨在利用地震数据部分频谱分量对地下介质模型参数信息进行模拟,然而由于地震激发、采集和接收系统的限制,带限特征是实际地震资料固有的缺陷,因此直接根据式(7)开展地震反演解释将会存在较强的不稳定性和不可靠性。

1.2 相对纵波阻抗模型约束

为了提高混合频率域地震反演方法的稳定性和可靠性,综合利用相对纵波阻抗低频模型约束方法。低频模型约束ζ往往通过实际测井数据或地质先验信息构建。常规的地震反演约束算法可以利用L2范数来衡量:

(8)

其中

1.3 快速多原子匹配追踪算法

贪婪匹配追踪算法是依据全局最优搜索方式,首先建立在过完备原子库F构建的基础上,并在过完备原子库中通过逐次迭代策略寻找最优匹配原子,最终将非平稳地震信号Y表征为所匹配原子ωi的线性组合形式:

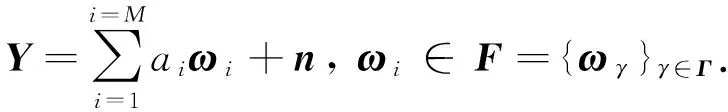
(9)

式中,Y为地震反射道集;ωi为匹配分解的原子;n为原始地震所包含的噪声;F为完备原子字典;ai为匹配原子相应振幅值。快速匹配算法则是利用一种批量筛选原子的策略,首先需要设定每一次匹配过程的硬迭代阈值ε,满足迭代阈值的内积原子将被列为候选匹配集合,具体表述为

|ci|≥α|εmax|,ci=〈ωi,Rs〉.

(10)

式中,ci为第i个原子与上次迭代残差的内积值;Rs为迭代残差向量;εmax为每次迭代内积向量中的绝对值最大值;α为迭代硬阈值,一般情况下0≪α≤1。假设地震信号经过N次迭代后,利用所匹配的M(M>N)个原子形成原子矩阵JN=[ω1,ω2,…,ωM]。然后,通过阻尼最小二乘算法逐次修正匹配原子振幅值,即

aN=[(JN)T(JN)+σ2I]-1(JN)TY.

(11)

式中,aN为第N次迭代修正后的振幅值;IM×M为单位矩阵;σ2为阻尼因子。假设YN为第N次迭代残差,可表示为

YN=Y-JNaN.

(12)

因此第N+1次迭代过程将会在剩余原子字典FN中进行,其更新的内机空间IPN可以表述为

IPN=〈YN,ωi〉,ωi∈FN.

(13)

经过第N+1次内积空间的搜索得到新的映射原子矩阵FN+1,且其下一步原子振幅aN+1的更新过程为

aN+1=[(FN+1)T(FN+1)+σ2I]-1(FN+1)TY.

(14)

稀疏反射系数地震反演是在常规反演方法的基础上,加入模型参数的稀疏性约束度量。匹配追踪稀疏反演方法主要是通过控制反射系数数量、迭代次数以及迭代阈值,经过有限步迭代搜索即可得到最优解。将式(7)、(8)和快速匹配追踪寻优算法联合起来,最终稀疏目标泛函为

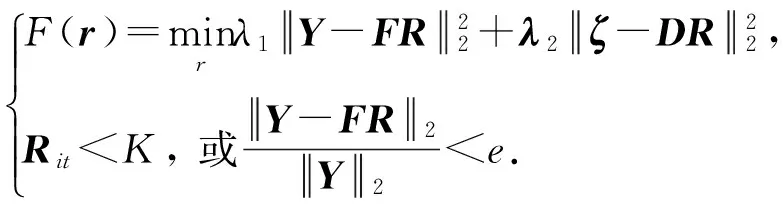
(15)

式中,K为迭代次数;e为硬迭代阈值。值得注意的是,K和e值的设定会影响反射系数反演的稀疏程度,实际处理过程中K的设定值可通过地质分层先验和测井曲线获得。当地震资料的信噪比较高时,K值的设定偏大,且e值的设定偏小,相应反演结果的地层分辨率提高。然而当地震资料的信噪比降低时,需要降低K值和升高e值。

通过求解式(15)得到相对反射系数值,地层的绝对波阻抗数值Ip(t)可以通过下面积分方程获得:

(16)

详细快速匹配追踪稀疏反演算法流程(图1)如下：

(1)选择信噪比较高的频率成分构建频率域核矩阵。

(2)输入有效频率成分构建的地震数据频谱S。

(3)构建相对纵波阻抗模型约束核矩阵。

(4)重新构建基于匹配追踪稀疏约束目标泛函。

(5)求解快速匹配反问题目标泛函及预设匹配参数设置。

(6)计算内积空间,确定满足迭代条件的第N次匹配原子数量和位置。

(7)建立所有匹配原子组成的核矩阵,利用阻尼最小二乘确定匹配原子振幅值。

(8)求取第N+1次迭代残差,构建剩余原子字典与更新内机空间。

(9)控制反射系数数量、迭代次数或迭代阈值,满足条件之一,结束迭代。

2 数据测试

2.1 一维模型试算

为了验证基于快速匹配追踪算法的稀疏反射系数反演方法的有效性,开展了1-D理论模型测试,采用30 Hz零相位Ricker子波(采样间隔1 ms)合成地震数据,如图2中黑线所示。

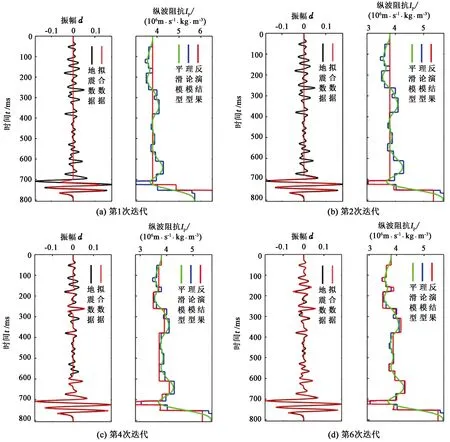
图2 快速匹配追踪频率域反演过程分析Fig.2 Analysis of frequency-domain inversion process with fast matching pursuit algorithm

图2(a)～(d)分别展示了第1次、2次、4次及6次迭代的反演结果。图中可见,理论模型中共包含21个反射系数,逐次迭代修正的反射系数个数超过1个,匹配的反射系数总个数依次为2、3、9及15。由于初始低频模型在反演过程中相比优势频带所占的比重较小,第1次迭代过程并未匹配出低频趋势,第2次迭代过程的低频成分得到了部分补偿,第4次迭代后低频成分得到了较好的补偿,第6次迭代后的稀疏反射系数基本得到恢复。图3(a)、(b)展示了逐次匹配迭代过程中地震与反射系数频谱的动态搜索过程。图3(c) 、(d)展示了地震和反射系数频谱的收敛曲线,容易看出,本文中频率域反演算法的收敛速度明显高于常规经典频率域匹配算法。

为了验证反演算法的抗噪能力,分析地震数据含不同程度噪声时的纵波阻抗恢复情况。图4(a)～(d)分别为无噪声、信噪比RSN=5、RSN=2及RSN=1情况下的纵波阻抗反演结果(其中黑线为理论含随机噪声地震数据,红色虚线为利用反演结果合成的地震数据)。图中可见,经过9次匹配搜索过程即可完成21个反射系数的有效恢复。无噪声情况下的反演结果基本和理论模型吻合,即使当地震数据受到强噪声干扰的时候(RSN=1),匹配追踪稀疏反演同样可以恢复出较可靠的纵波阻抗数据。

由于匹配追踪稀疏反演是建立在地层模型块化假设的基础上展开,因此本文中利用实际测井数据建立渐变地层模型验证该方法的普适性。如图5所示为渐变地层模型在含不同噪声情况的快速匹配反演及拟合误差分析,无噪声情况下迭代次数为32次,然而随着含噪声程度的不断增加应逐渐减小迭代次数以及迭代阈值,以此来降低弱小高频噪声干扰对反演过程的影响,该预测结果与渐变地层理论模型吻合较好。

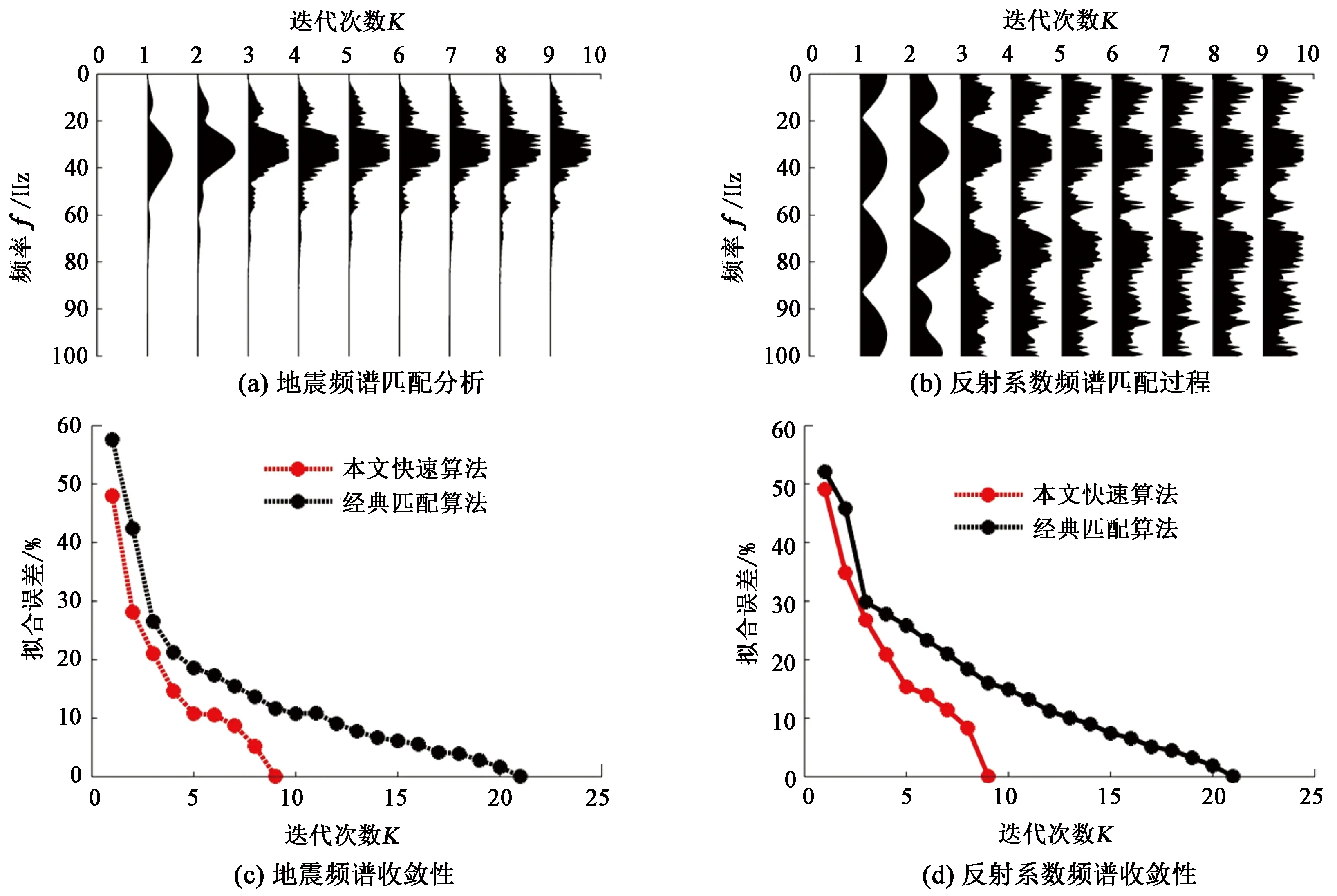
图3 无噪声情况下地震与反射系数频谱动态匹配搜索过程分析Fig.3 Analysis of dynamic matching pursuit process for seismic and reflection spectrum without noise pollution

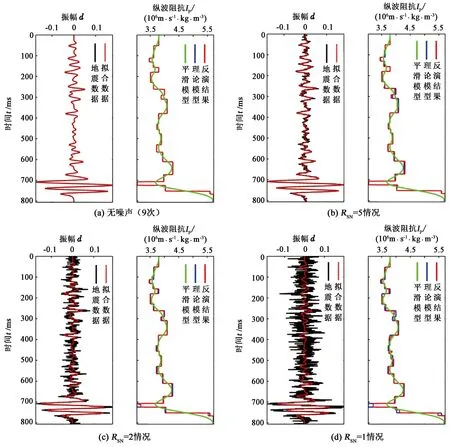
图4 块化地层模型不同噪声情况下反演结果及拟合误差Fig.4 Inversion results and fitting errors under the condition of different noise levels by blocky model

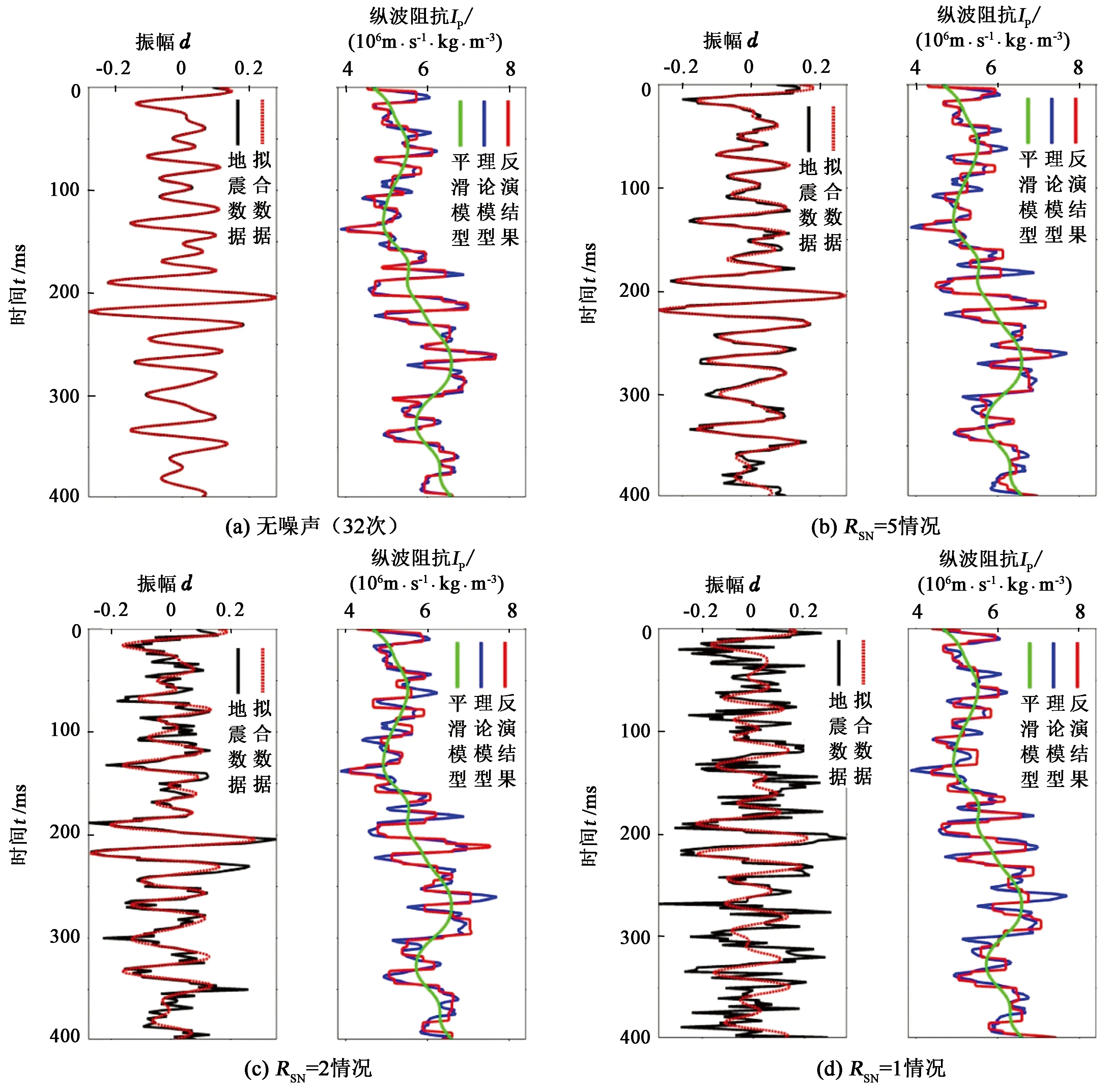
图5 渐变地层模型不同噪声情况下反演结果及拟合误差Fig.5 Inversion results and fitting errors under the condition of different noise levels by continuous model

2.2 二维模型试算

针对理论Overthrust逆掩断层模型(图6(a))展开了反演算法的测试,该模型共包含641道,采用30 Hz零相位雷克子波合成地震记录,纵向时间长度为720 ms,如图6(b)所示,其中蓝线为CDP100和CDP480位置处的理论纵波阻抗曲线。图6(c)、(d)为无噪声情况反射系数和纵波阻抗的反演结果,其中红色虚线为CDP100和CDP480处的反演结果。对比理论模型,可以看出无噪声情况下反演结果的预测精度较高,即使在河道砂(黑色椭圆)位置的反演结果同样保持较高的吻合度。

图6(e)、(f)为含10%随机噪声情况下的反演结果。由图可见,反演结果受到一定程度的噪音污染,但是整体上仍然保持着与理论模型较高的一致性,微弱异常体同样可以得到较好的预测。通过Overthrust逆掩断层模型的理论测试更有力地说明了该方法在地下介质构造复杂的情况下,同样可以保证较高的地层分辨率。

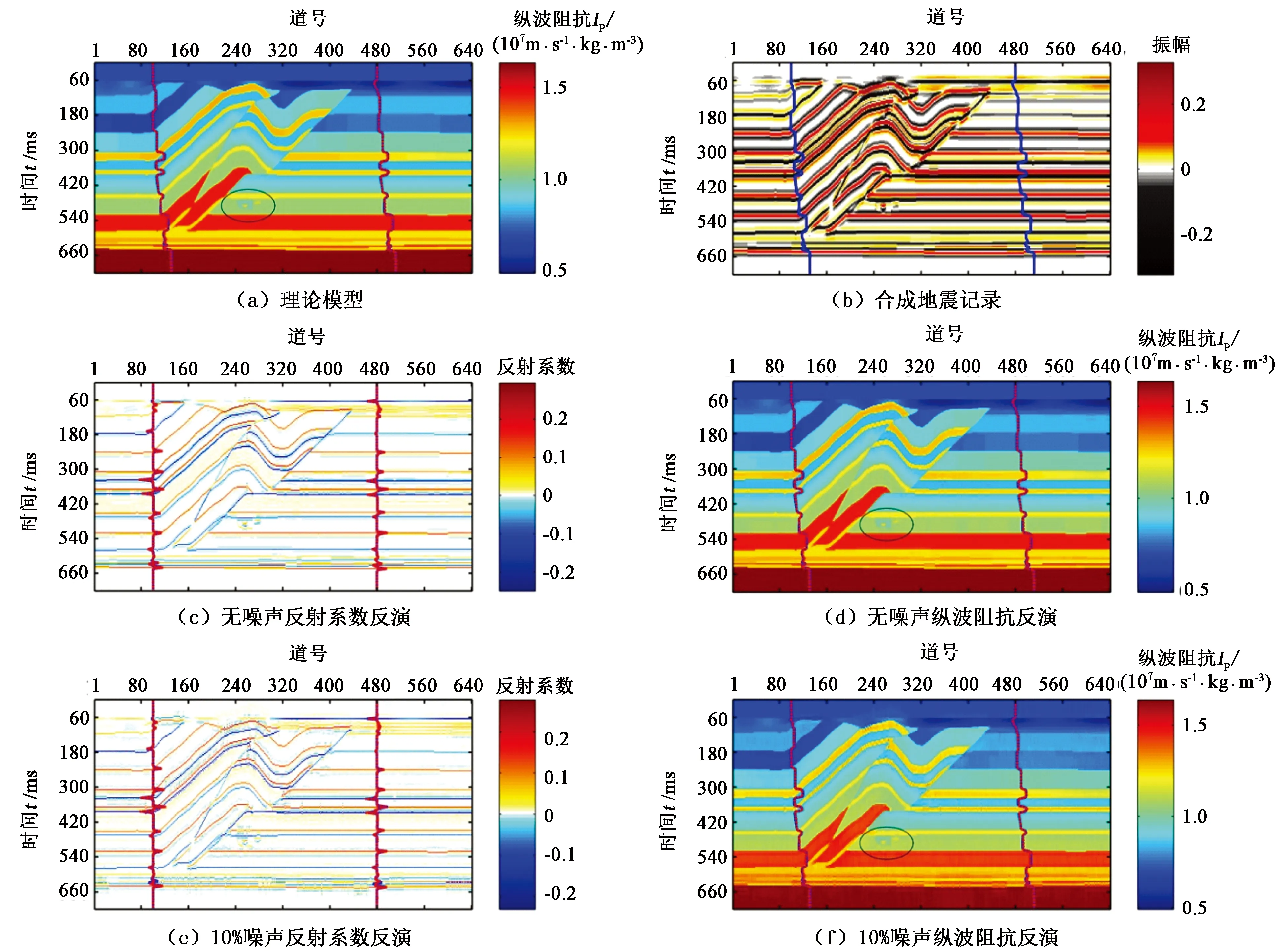
图6 Overthrust逆掩模型不同噪声情况下反演结果Fig.6 Inversion results of overthrust model under different noise levels with fast matching pursuit algorithm

3 实际资料处理

为更进一步验证快速匹配追踪频率域稀疏反射系数反演的实用性,从中国某东部F探区的勘探实例中抽取一条测线,如图7(a)所示为叠后地震剖面,其中A井位置处为该井的实测纵波阻抗变密度显示。为了得到更加可靠的地下模型参数信息,首先需要结合测井数据建立初始低频模型,如图7(b)所示为利用测井数据建立的低频模型,由于测井数据有效频带范围与地震数据的频带存在较大的差异,因此测井数据中包含的高频成分不应该包含在基于地震数据的模型参数反演过程中。

为了说明本方法与常规地震反演在可靠性与分辨率方面存在的差异,如图7(c)为常规贝叶斯时间域地震反演结果,图7(d)为本文快速匹配追踪频率域反演得到的高分辨率反射系数剖面,利用道积分得到纵波阻抗剖面如图7(e)所示。图中可见,虽然本方法是逐道进行反射系数反演的,但反演结果仍然保持着较高的横向连续性。值得一提的是,对比常规时间域阻抗反演方法和快速匹配追踪频率域稀疏反演的结果可以发现,快速匹配追踪频率域反演在地层分辨率方面要优于常规时间域地震反演方法,如图中椭圆和矩形框区域所示,且本方法的块化地层剖面相比连续变化地层剖面更加有利于地层的划分。反演剖面中显示的为A井实测纵波阻抗的变密度显示方式,容易看出,反演结果与测井数据保持着较高的一致性,进一步说明该方法具有较高的反演可靠性。

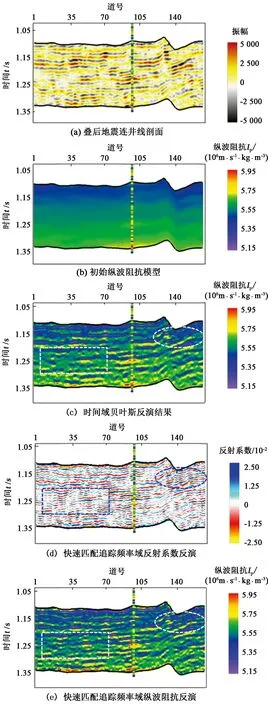
图7 利用不同地震反演方法实现的纵波阻抗预测结果Fig.7 Estimated impedance results in one field case with different inversion methods

4 结 论

(1)混合频率域褶积算子相比时间域算子具有频率选择自由的优点,有助于利用高信噪比的频率成分提高反演的抗噪能力。

(2)相对纵波阻抗低频约束可以较好地解决部分频谱目标泛函收敛性和稳定性问题,进而有效缩小模型参数最优空间。

(3)多原子快速匹配追踪算法可以提高收敛速度,改善经典匹配追踪反演存在的计算效率低问题。

(4)多原子逐次匹配搜索比单原子搜索具有更高的收敛精度,避免单原子搜索容易陷入局部极值的问题。

[1] 李坤,印兴耀,宗兆云.利用平滑模型约束的频率域多尺度地震反演[J].石油地球物理勘探,2016,51(4):760-768.

LI Kun, YIN Xingyao, ZONG Zhaoyun. Seismic multi-scale inversion in the frequency domain based on smooth model constraint[J]. Oil Geophysical Prospecting, 2016,51(4):760-768.

[2] TARANTOLA A. Inverse problem theory and methods for model parameter estimation[J]. Soc Ind Appl Math, 2005,9(5):1597-1620.

[3] TIKHONOV A. Solution of incorrectly formulated problems and the regularization method[J]. Sov Math Dokl, 1963,5:1035-1038.

[4] ALEMIE W, SACCHI M. High-resolution three-term AVO inversion by means of a Trivariate Cauchy probability distribution[J]. Geophysics, 2011,76(3):R43-R55.

[5] ZONG Zhaoyun, YIN Xingyao, WU Guochen. Geofluid discrimination incorporating poroelasticity and seismic reflection inversion[J]. Surveys in Geophysics, 2015,36(5):659-681.

[6] YIN Xingyao,ZHANG Shixin. Bayesian inversion for effective pore-fluid bulk modulus based on fluid-matrix decoupled amplitude variation with offset approximation[J]. Geophysics, 2014,79(5):R221-R232.

[7] 印兴耀,刘倩.致密储层各向异性地震岩石物理建模及应用[J].中国石油大学学报(自然科学版),2016,40(2):52-58.

YIN Xingyao, LIU Qian. Anisotropic rock physics modeling of tight sandstone and applications[J]. Journal of China University of Petroleun (Edition of Natural Science), 2016,40(2):52-58.

[8] 吴飞,范宜仁,邓少贵,等.储层岩石T2-G实验采集参数自动匹配技术研究[J].中国石油大学学报(自然科学版),2014,38(4):50-56.

WU Fei, FAN Yiren, DENG Shaogui, et al. Automatic matching technology for determining acquisition parameters of formation rockT2-Gexperiment[J]. Journal of China University of Petroleun (Edition of Natural Science), 2014,38(4):50-56.

[9] NGUYEN T, CASTAGNA J. High resolution seismic reflectivity inversion[J]. Journal of Seismic Exploration, 2010,19(4):303-320.

[10] WANG Y. Seismic time-frequency spectral decomposition by matching pursuit [J]. Geophysics, 2006,72(1):V13-V20.

[11] WANG Y. Multichannel matching pursuit for seismic trace decomposition [J]. Geophysics, 2010,75(4):V61-V66.

[12] MALLAT S, ZHANG Z. Matching pursuits with time-frequency dictionaries[J]. IEEE Transactions on Signal Processing, 1993,41(12):3397-3415.

[13] 张繁昌,李传辉,印兴耀.基于动态匹配子波库的地震数据快速匹配追踪[J].石油地球物理勘探,2010,45(5):667-673.

ZHANG Fanchang, LI Chuanhui, YIN Xingyao. Seismic data fast matching pursuit based on dynamic matching wavelet library[J]. Oil Geophysical Prospecting, 2010,45(5):667-673.

[14] 张繁昌,李传辉,印兴耀.三角洲砂岩尖灭线的地震匹配追踪瞬时谱识别方法[J].石油地球物理勘探,2012,47(1):82-88.

ZHANG Fanchang, LI Chuanhui, YIN Xingyao. Delta fringe line recognition based on seismic matching pursuit instantaneous spectral characteristics[J]. Oil Geophysical Prospecting, 2012,47(1):82-88.

[15] 李坤,印兴耀,宗兆云.基于匹配追踪谱分解的时频域FAVO流体识别方法[J].石油学报,2016,37(6):777-786.

LI Kun, YIN Xingyao, ZONG Zhaoyun. Time frequency domain FAVO fluid discrimination method based on matching pursuit spectrum decomposition[J]. Acta Petrolei Sinica, 2016,37(6):777-786.

[16] ØZBEK A, ÖZDEMIR A, VASSALLO M.Interpolation by matching pursuit [C/OL]//2009 SEG Annual Meeting, Houston City, October25-30, 2009: SEG Technical Program Expanded Abstracts [2014-10-09].http://library.seg.org/doi/abs/10.1190/1.3255534.

[17] CHOI J, BYUN J, SEOL S J, et al. Wavelet based interpolation by matching pursuit and multicomponent streamer data[C/OL]//2014 SEG Annual Meeting, Denver City,October 26-31, 2014: SEG Technical Program Expanded Abstracts[2015-12-10].http://library.seg.org/doi/abs/10.1190/segam2014-1492.1.

[18] SCHONEWILLE M, YAN Z, BAYLY M, et al. Matching pursuit Fourier interpolation using priors derived from a second data set [C/OL]//2013 SEG Annual Meeting, HoustonCity, September 22-27, 2013: SEG Technical Program Expanded Abstracts [2016-02-08].http://library.seg.org/doi/abs/10.1190/segam2013-0956.1.

[19] VASSALLO M, ÖZBEK A J, ÖZDEMIR K, et al. Crossline wavefield reconstruction from multi-component streamer data: multichannel interpolation by matching pursuit [C/OL]//2010 SEG Annual Meeting, Denver City, October 17-28, 2010: SEG Technical Program Expanded Abstracts [2015-05-10].http://library.seg.org/doi/abs/10.1190/1.3513597.

[20] WEN X, ZHANG B, PENNINGTON W, et al. Relative P-impedance estimation using a dipole-based matching pursuit decomposition strategy[J]. Interpretation, 2015,3(4):T197-T206.

[21] FENG F, LEI G, ZHANG Y, et al. Matching pursuit inversion modeling based on true depth calibration and its applications[C/OL]//2015 SEG Annual Meeting, New Orleans City, October 18-22, 2015: SEG Technical Program Expanded Abstracts[2015-09-08].http://library.seg.org/doi/abs/10.1190/segam2015-5841552.1.

[22] RODRIGUEZ I, SACCHI M, GU Y. Continuous hypocenter and source mechanism inversion via a Greens function-based matching pursuit algorithm [J]. The Leading Edge, 2010,29(3):334-337.

[23] 刘杰,张忠涛,刘道理,等.强反射背景下沉积体边界检测及流体识别方法[J].石油物探,2016,55(1):142-149.

LIU Jie, ZHANG Zhongtao, LIU Daoli, et al. Sediment boundary identification and fluid detection for the seismic data with strong background reflections[J]. Geophysical Prospecting for Petroleum, 2016,55(1):142-149.

[24] 李海山,杨午阳,田军,等. 匹配追踪煤层强反射分离方法[J]. 石油地球物理勘探,2014,49(5):866-870.

LI Haishan, YANG Wuyang, TIAN Jun, et al. Coal seam strong reflection separation with matching pursuit[J]. Oil Geophysical Prospecting, 2014,49(5):866-870.

[25] 朱博华,向雪梅,张卫华,等.匹配追踪强反射层分离方法及应用[J]. 石油物探,2016,55(2):280-287.

ZHU Bohua, XIANG Xuemei, ZHANG Weihua, et al. Strong reflection horizons separation based on matching pursuit algorithm and its application [J]. Geophysical Prospecting for Petroleum, 2016,55(2):280-287.

[26] 陈胜,欧阳永林,曾庆才,等. 匹配追踪子波分解重构技术在气层检测中的应用[J]. 岩性油气藏,2014,26(6):111-114.

CHEN Sheng, OUYANG Yonglin, ZENG Qingcai, et al. Application of matching pursuit wavelet decomposition and reconstruction technique to reservoir prediction and gas detection[J]. Geophysical Prospecting for Petroleum, 2014,26(6):111-114.

[27] 赵天姿,宋炜,王尚旭.基于匹配追踪算法的时频滤波去噪方法[J]. 石油物探,2008,47(4):367-371.

ZHAO Tianzi, SONG Wei, WANG Shangxu. Time-frequency filtering de-noise method based on matching pursuit algorithm[J]. Geophysical Prospecting for Petroleum, 2008,47(4):367-371.

[28] HU H, LIU Y, OSEN A, et al. Compression of local slant stacks by the estimation of multiple local slopes and the matching pursuit decomposition [J]. Geophysics, 2015,80(6):WD175-WD187.

[29] WANG B, PANN K. Kirchhoff migration of seismic data compressed by matching pursuit decomposition [C/OL]//1996 SEG Annual Meeting, Denver City, November 10-15, 1996: SEG Technical Program Expanded Abstracts [2014-03-18].http://library.seg.org/doi/abs/10.1190/1.1826441.

[30] MARGRAVE G. Theory of nonstationary linear filtering in the Fourier domain with application to time-variant filtering [J]. Geophysics, 1998,63(1):244-259.

[31] YIN Xingyao, LI Kun, ZONG Zhaoyun. Resolution enhancement of robust Bayesian pre-stack inversion in the frequency domain[J]. Journal of Geophysics and Engineering, 2016,13(5):646-656.