微裂缝对致密多孔介质中气体渗流的影响机制

赵建林, 姚 军, 张 磊, 杨永飞, 孙 海, 孙致学, 白玉湖

(1.中国石油大学石油工程学院,山东青岛 266580; 2.中海油研究总院，北京 100028)

水平井钻井及大规模水力压裂技术的进步使页岩油气与致密油气等非常规油气资源的开发成为可能,作为一类重要的非常规油气资源,页岩气的开发正受到越来越多的关注[1-4]。页岩气藏的孔隙尺寸非常小,通常在纳米级[5-6],渗透率极低,在不采取压裂等改造措施的情况下无工业产能。水平井钻井能够增加井筒与储层间的接触面积,从而增大地层到井筒内的流量,而大规模水力压裂能够在地层中压裂产生水力大裂缝以及次生的小裂缝,并与页岩气藏中自生的一些微裂缝相连,在储层中构成裂缝网络,裂缝网络的形成是页岩气藏得以工业化开发的关键。尽管页岩气藏的开发已经在美国取得了巨大成功[7],页岩气在纳米级孔隙中的渗流机制还未完全研究透彻[2],尤其是当微裂缝存在时微裂缝对页岩这种致密多孔介质中气体渗流的影响机制目前研究很少。由于页岩储层孔隙尺寸主要在纳米级,气体在其中的流动不同于在常规孔隙中的流动[8-9],属于微纳尺度气体流动,流动特征参数为努森数(Kn),其定义为分子平均自由程与流动特征长度的比值。根据努森数可将流动划分为连续流区(Kn≤0.001)、滑移流区(0.00110)4个区域[10]。当Kn≤0.1,即流动处于连续流区和滑移流区时,连续介质假设成立,流动可以采用无滑移或滑移边界的Navier-Stokes(N-S)方程进行描述;当Kn>0.1以后连续介质假设不再成立,须采用基于粒子的流动模拟方法,如分子模拟(MD)方法[11]、直接模拟蒙特卡洛方法(DSMC)[12]、格子Boltzmann方法(LBM)[7]等。由于MD方法和DSMC方法模拟区域都非常小,不适用于孔隙尺度上的流动模拟,而LBM计算效率更高,能够进行孔隙尺度上的流动模拟。目前已有不少学者采用LBM进行页岩气的流动模拟,Fathi等[13]、Zhang等[14]、宁正福等[15]和姚军等[16]模拟了简单规则纳米通道中的页岩气流动规律;张磊等[17]、孙海等[18]、Zhao等[19-20]将LBM应用到了三维数字岩心中,模拟了真实页岩岩心中的气体流动;张磊等[21]、Zhao等[22]分别采用不同的LB模型研究了页岩有机质中的解吸/扩散机制;Zhang等[23]进行了页岩中气水两相流动模拟,研究了压裂液反排率低的原因;Chen等[24]提出了考虑Klinkenberg效应的表征单元体(REV)尺度LB模型,并采用该模型研究了微裂缝对页岩气渗流的影响。尽管前人已采用LBM进行了大量的页岩气流动模拟及研究工作,但大多数学者都针对页岩基岩中的气体流动机制进行研究,很少有学者在孔隙尺度上对微裂缝的影响开展研究。笔者采用LBM在孔隙尺度上开展裂缝性致密多孔介质中的气体流动模拟,揭示微裂缝对致密多孔介质中气体渗流的影响机制。

1 微尺度格子Boltzmann模型

构建能够考虑努森层影响、高压影响以及微尺度效应的LB模型[16],该模型适用于平板模型中不同努森数下的气体流动模拟,但对于多孔介质,该模型仅适用于低努森数下的气体流动模拟,要进行高努森数下多孔介质中的气体流动模拟,模型中必须引入正则化过程[25-26]。

1.1 基本模型

采用单松弛时间LB模型进行流动模拟,离散速度模型采用二维九速(D2Q9)模型,演化方程如下(如无特殊说明,本文中所使用变量均为无因次格子单位):

(1)

其中

式中,α为离散速度方向,α=0,1,2,…,8;fα为离散速度空间α方向上的分布函数;r为粒子的空间位置;eα为α方向的速度;t为时间;δt为时间步长;τ为弛豫时间;fαeq为离散速度空间的局部平衡态分布函数;Fα为α方向上所受到的外力;ρ和u为宏观的粒子密度和速度;cs为格子声速;wα为权系数;a为外力加速度。

采用单组份Shan-Chen模型[27]引入Peng-Robinson(P-R)状态方程进行流动模拟,详细过程见文献[16]。

1.2 松弛时间和边界条件

对于微尺度气体流动,考虑气体稠密性和努森层的影响可得有效松弛时间和努森数存在以下关系[16, 28-29]:

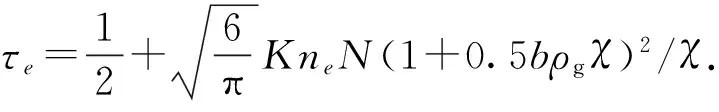
(2)

其中

0.038 6(bρg)4.

式中,H为特征长度,m;δx为每个网格长度,m;d和m分别为分子直径和分子质量,对于甲烷有d=0.38 nm,m=2.658×10-26kg;ρg为气体密度,kg/m3;χ为气体稠密性引起的碰撞修正因子。

由于多孔介质固体壁面非常粗糙,漫反射边界条件非常适用该类边界,在LBM中漫反射边界条件的离散格式[30-31]为

fα=Kfαeq(ρw,uw), (eα-uw)·n>0.

(3)

其中

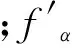
在进行多孔介质中气体流动模拟前,首先要搜寻所有固体边界节点,并确定每个边界节点i指向孔隙内的法向方向ni,然后进行流动模拟,在满足(eα-uw)·ni>0的方向上执行漫反射边界条件,否则,执行反弹边界条件。

1.3 正则化过程

由于D2Q9离散速度模型的限制,分布函数的非平衡态部分包含高阶(高于二阶)项信息,在D2Q9模型下具有较强的各向异性,当努森数较大时,该部分会引入较大误差,而正则化过程可以过滤掉高阶项信息,使模型在D2Q9离散速度模型下保持较好的各向同性[26,32]。因而要进行高努森数下多孔介质中的气体流动模拟,需要在模型中引入正则化过程[26,32],引入正则化过程后演化方程变为

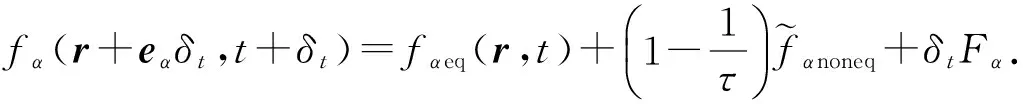
(4)

其中

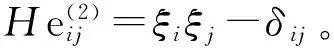
1.4 局部努森数计算

对于微尺度气体流动,其特征参数为努森数,根据努森数定义[16],有

(5)

气体在孔隙中流动的特征长度H为孔隙尺寸,对于多孔介质,其孔隙尺寸随机分布,不是定值,因而需要引入局部特征长度。在进行流动模拟前,首先计算所有孔隙节点所对应的孔隙尺寸,即特征长度H(r);并选取参考特征长度Href和参考压力对应的参考密度ρref和参考修正因子χref,计算该状态下对应的参考努森数Knref;然后进行流动模拟,每个孔隙节点上的局部努森数计算式为

(6)

2 模型验证

为验证模型的准确性及正则化过程的必要性,分别采用本文中模型和不考虑正则化过程的LB模型进行二维多孔介质中的外力驱动流动模拟,并与MD模拟结果[33]进行对比。物理模型如图1所示,为保证较小流速,模拟时选取外力加速度为0.000 05,流动对应的努森数为0.11,模拟终止条件为

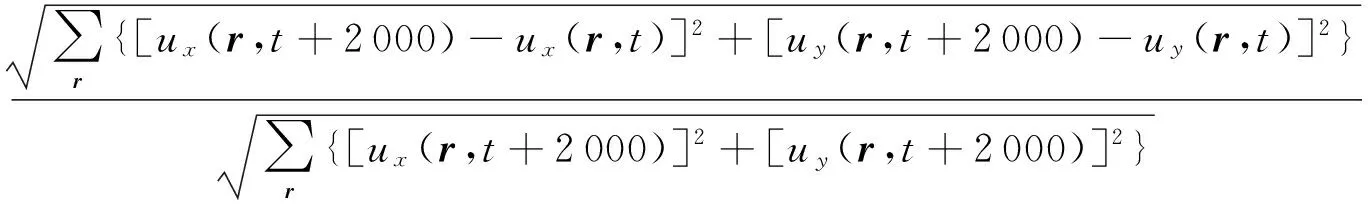
(7)

图1 含障碍物平板模型示意图Fig.1 Physical model of gas flow around a square cylinder in a nanochannel

当模拟达到稳定时结果如图2所示。由图2可以看出,本文中模型的模拟结果与MD模拟结果具有较好的一致性,而不考虑正则化过程的LB模型会出现非物理的流速分布,验证了本文中模型进行多孔介质中微尺度气体流动模拟的准确性及正则化过程的必要性。

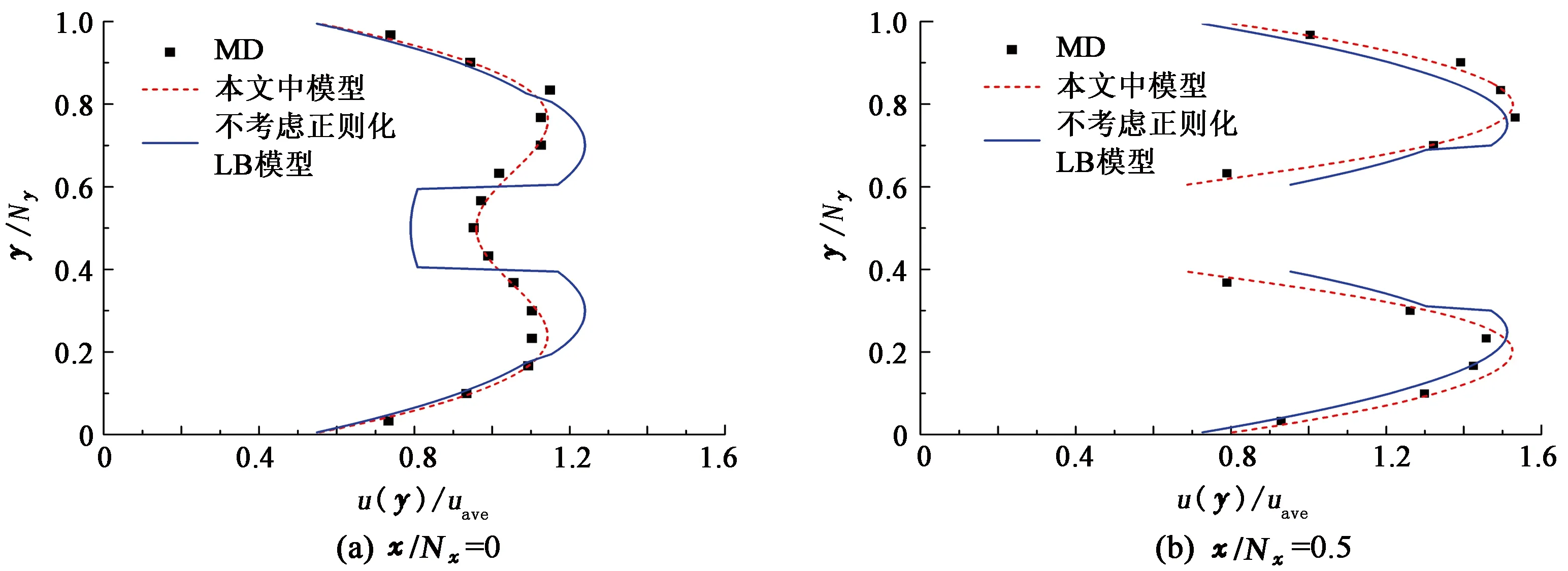
图2 MD模拟结果与LBM模拟结果对比Fig.2 Comparison of MD simulation results with LBM simulation results

3 微裂缝对致密多孔介质中气体渗流的影响机制

3.1 基于LBM的致密多孔介质中气体流动模拟

Chalmers等[35]利用场发射扫描电子显微镜和透射电子显微镜对不同地区的页岩岩样进行了分析,发现页岩孔隙尺寸中位数由几纳米到几十纳米,并且页岩中发育有纳米尺度微裂缝,为研究微裂缝对致密多孔介质中气体渗流的影响机制,随机重构了二维多孔介质模型,选取其平均孔隙尺寸为40 nm,并在多孔介质中分别增加了两条相连及不相连的微裂缝,微裂缝开度取130 nm,采用以上模型研究微裂缝对致密多孔介质中气体渗流的影响,如图3所示。模拟区域为313×495网格,网格分辨率均为5 nm。

图3 不同二维多孔介质模型示意图Fig.3 Schematic of different porous media

图4所示为3个多孔介质的孔隙尺寸分布,由于多孔介质b和c中含有微裂缝,其孔隙尺寸分布表现为双峰分布,3个多孔介质孔隙度分别为0.536 0、0.604 5和0.605 1。

采用构建的微尺度格子Boltzmann模型进行甲烷在3种多孔介质中的压力驱动流动模拟,上下入、出口采用压力边界条件,左右边界为固体边界,采用滑移边界条件,模拟温度为298 K,出口压力分别取0.02、0.05、0.1、0.2、0.5、1.0、2.0、5.0和10.0 MPa,为保证驱动压力梯度一致,在所有模拟中入出口压差均为0.005 MPa,模拟终止条件如式(7)所示。

图4 不同多孔介质中孔隙尺寸分布Fig.4 Pore size distributions of different porous media

3.2 微裂缝对致密多孔介质中气体渗流的影响

当模拟达到稳定后,分别统计不同压力下通过3种多孔介质的气体流量,并通过达西定律计算其对应的表观渗透率ka,结果如图5(a)所示。由图5(a)可知,压力对表观渗透率具有重要影响,随着压力降低,多孔介质的表观渗透率逐渐增大,这与之前单管中的流动模拟结果一致[16]。这是因为气体在多孔介质中的流动由气体分子间的相互碰撞和气体分子与壁面间的相互碰撞驱动,气体分子与壁面间的相互碰撞会在壁面产生滑移流速。随着压力降低,气体分子间距变大,分子运动的平均自由程变大,气体分子与壁面的碰撞所占比例增大,壁面滑移速度变大,微尺度效应增强,多孔介质表观渗透率增大。此外,裂缝的存在能够明显增大渗透率,裂缝性多孔介质的的表观渗透率一直位于基岩多孔介质的上方,这是因为裂缝的存在为气体流动提供了高渗通道,减小了整个多孔介质中的渗流阻力,提高了渗透率,并且连通性裂缝的影响更明显。

为进一步分析微裂缝对致密多孔介质中气体渗流的影响,计算裂缝性多孔介质相对表观渗透率与压力的关系,结果如图5(b)所示,其中相对表观渗透率定义为某压力下裂缝性多孔介质的表观渗透率与该压力下不包含裂缝的基岩多孔介质的表观渗透率之比,反映了微裂缝对致密多孔介质中气体渗流的影响。由图5(b)可知,随着压力增加,微裂缝提高致密介质渗透率的作用增强,且连通性裂缝的影响更明显;在高压和低压下,裂缝对提高致密多孔介质表观渗透率的作用趋于稳定,而在中间压力范围内,随着压力升高,裂缝对提高致密多孔介质表观渗透率的作用迅速增强。由模拟结果可知,在致密气藏的开发过程中,初期压力大,多孔介质的表观渗透率低,储层中自生或采取压裂改造后产生的裂缝,能够明显改善储层的渗透性;随着气藏压力的降低,多孔介质的表观渗透率逐渐增大,但裂缝的作用相对减弱。

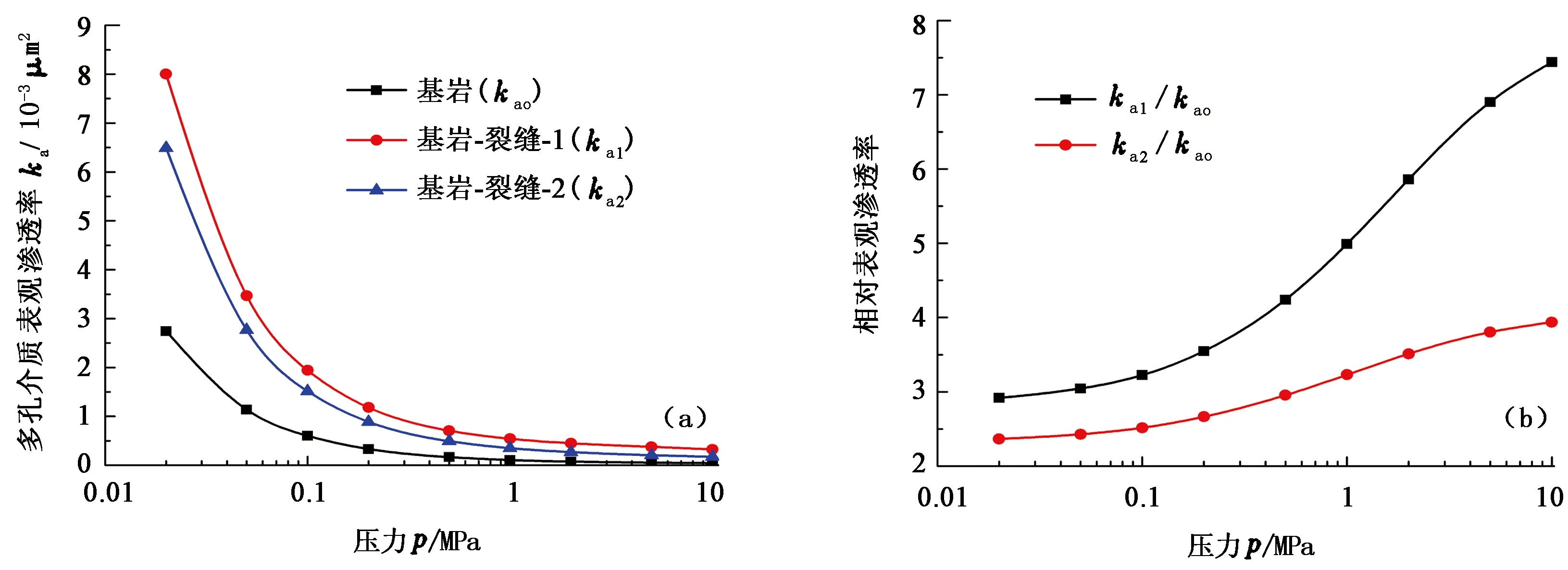
图5 微裂缝对致密多孔介质渗透率的影响Fig.5 Effects of micro-fractures on permeability of tight porous media

3.3 裂缝性致密多孔介质中气体渗流规律

不同压力下裂缝性多孔介质中的无因次流速分布如图6所示。无因次流速定义为多孔介质中某点的流速与多孔介质中最大流速之比。由图6可知,裂缝在多孔介质中构成了高渗通道,裂缝中的气体流速明显高于基岩中的气体流速;对于连通性裂缝,从入口到出口之间裂缝构成了与基岩并联的高渗通道,气体通过裂缝迅速从入口流向出口,其提高多孔介质渗透率效果明显;而对于非连通裂缝,在压力降落方向上裂缝也能构成与基岩并联的高渗通道,但两个高渗通道被渗透率较低的基岩隔断,因而其仍能提高多孔介质的渗透率,但其影响相对较弱。此外,与裂缝中气体流速相比,高压下与裂缝并联的基岩中气体流速极低,几乎可以忽略;而随着压力的降低,基岩中的无因次气体流速逐渐增大,其对多孔介质中气体流量的贡献提升。

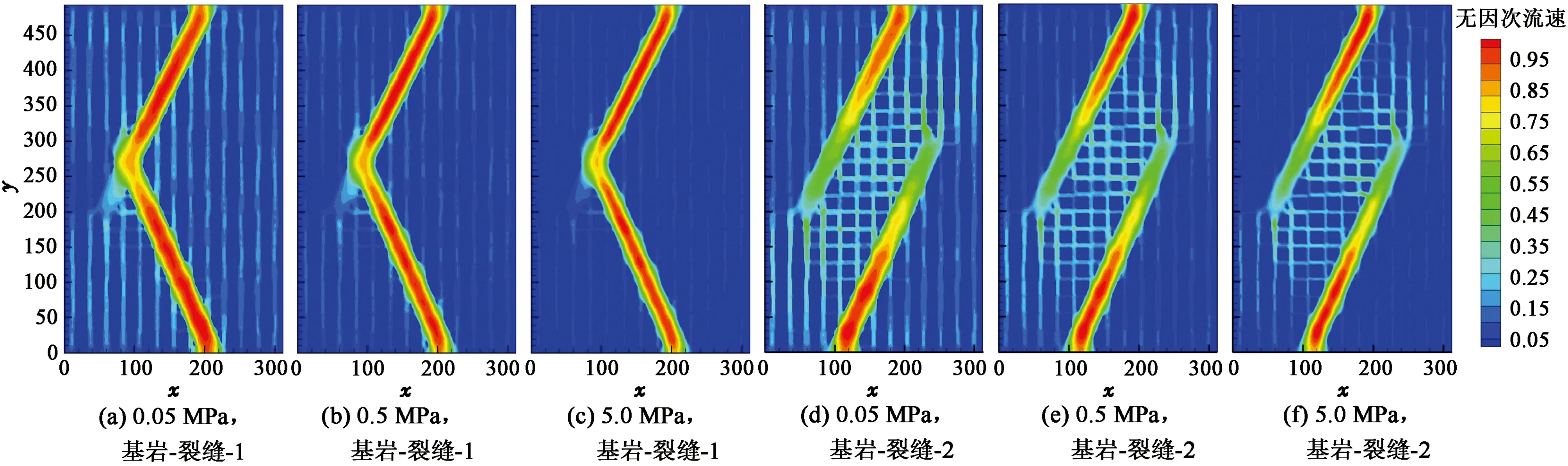
图6 不同裂缝性多孔介质中无因次流速分布Fig.6 Dimensionless velocity distributions in different fractured tight porous media

分别统计裂缝孔隙与基岩孔隙中的平均流速,并计算得到裂缝与基岩中平均流速比与压力的关系,如图7所示。图7中曲线变化规律与图6中结论一致,即随着压力的升高,基岩与裂缝中的流速差别越来越大;且当压力极大或极小时,裂缝与基岩中平均流速比趋于定值,而在中间压力范围,随着压力的升高,裂缝与基岩中流速差别迅速增大。

图7 裂缝性多孔介质裂缝与基岩中平均流速比与压力的关系Fig.7 Relationship between average velocity ratio in fractures and matrix and pressure

3.4 微裂缝对致密多孔介质中气体渗流的影响机制

微裂缝能够提高致密多孔介质渗透率的主要原因是在压降方向上微裂缝与基岩形成了并联高渗通道,构建二维并联通道模型分析微裂缝对致密多孔介质气体渗流的影响机制,结果如图8所示。其中5条通道的宽度分别为10、15、20、25、30个网格,模型分辨率均为5 nm/网格,图8中较小孔隙可以等效为基岩孔隙而较大孔隙可以等效为裂缝孔隙。采用微尺度格子Boltzmann模型进行压力驱动甲烷流动模拟,模拟温度为298 K,出口压力分别为0.01、0.2、1.0和20.0 MPa,为保持压力梯度一致,入出口压差均为0.001 MPa。

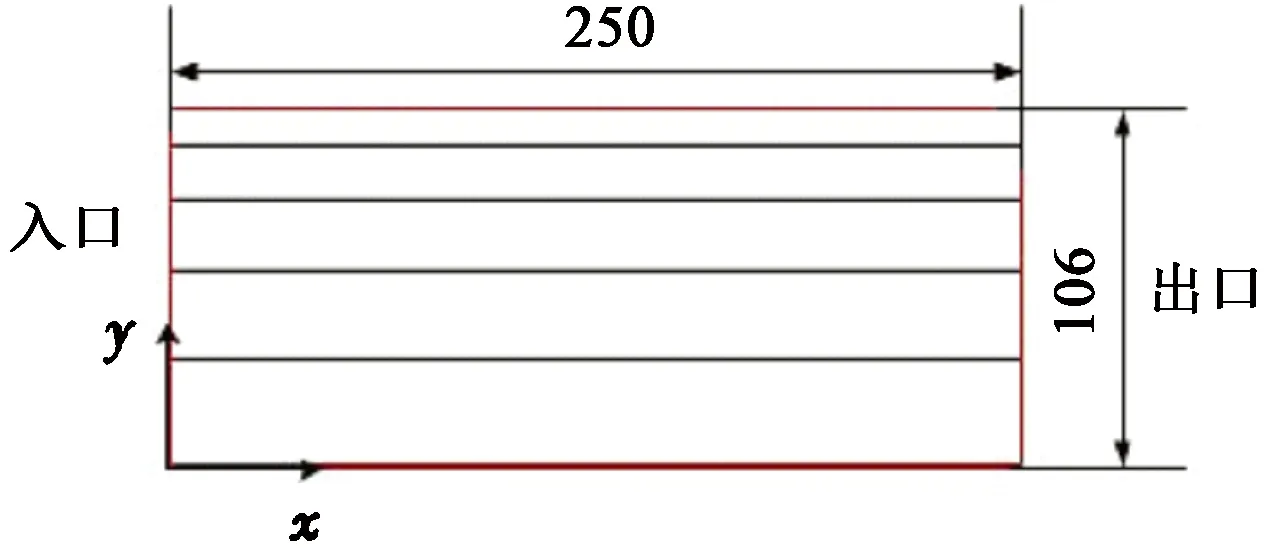
图8 二维并联通道模型示意图Fig.8 Schematic of parallel slit pore model

当模拟达到稳定后得到并联通道模型中的无因次流速分布如图9所示。当压力较高时气体分子间距很小,分子运动的平均自由程很小,无论大孔还是小孔中气体流动对应的努森数都较小,孔隙中的流动主要由气体分子间相互碰撞引起的黏性流控制,气体分子与壁面间的碰撞所占比例很小,壁面滑移速度很小,与小孔相比大孔中存在更多的分子间相互碰撞,因而大孔与小孔中流速差别较大。随着压力降低,气体分子间距变大,气体分子运动的平均自由程变大,孔隙中努森数变大,气体分子与壁面间的相互碰撞所占比例增大,壁面滑移速度增大,因而多孔介质中气体流动阻力减小,表观渗透率增大;并且小孔的特征长度更小,其努森数更大,壁面滑移更明显,气体流动阻力减小更明显,因而大孔与小孔的流速差别减小。当压力降低到一定值后,无论在大孔还是小孔中气体流动对应的努森数都很大,孔隙中的流动主要由气体分子与壁面间相互碰撞引起的努森流控制,微尺度效应在不同孔隙中的影响趋于一致,因而大孔与小孔中的流速差别趋于一致。这就是造成图7中流动规律的原因。

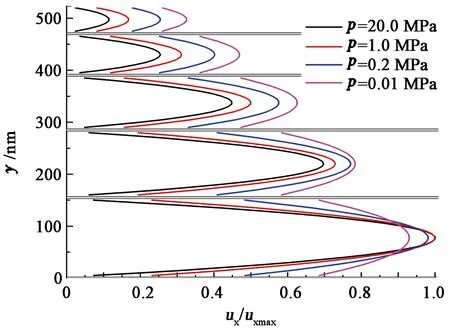
图9 并联通道模型中x=125截面上不同压力下无因次流速分布Fig.9 Dimensionless velocity distributions in parallel slit model at slice x=125 under different pressures

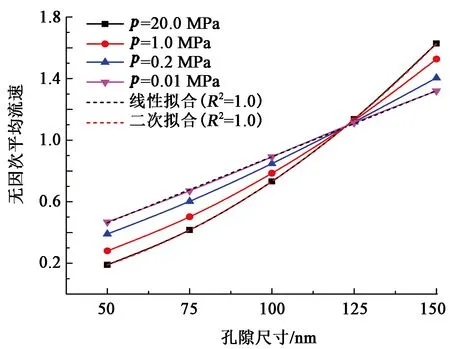
图10 并联模型中不同压力下无因次平均流速与孔隙尺寸的关系Fig.10 Relationship between dimensionless average velocity and pore size under different pressures

为定量分析微裂缝对致密多孔介质中气体渗流的影响机制,统计得到了不同压力下无因次平均流速与孔隙尺寸的关系,如图10所示。其中无因次平均流速定义为某一尺寸孔隙中气体平均流速与多孔介质整体平均流速之比。由图10可知,随着压力的降低,大孔中无因次平均流速减小,而小孔中无因次平均流速增大,大孔与小孔中的流速差别变小。并且在高压下,无因次平均流速与孔隙尺寸为二次函数关系,而在低压下,无因次平均流速与孔隙尺寸为线性函数关系。

对以上现象进行分析,对于二维平板模型,其固有渗透率为kintrinsic=H2/12,考虑微尺度效应后其表观渗透率可用Klinkenberg模型[34]描述:

kapp=kintrinsic(1+6Kn).

(8)

对于该并联通道模型,当压力很高时努森数很小,如当压力为20.0 MPa时5个通道中的努森数分别为0.003 2、0.002 1、0.001 6、0.001 3和0.001 1,此时有kapp≈kintrinsic=H2/12,多孔介质表观渗透率对孔隙尺寸敏感,由于流速正比于表观渗透率,因而流速与孔隙尺寸也为二次函数关系。当压力很低时努森数很大,如当压力为0.01 MPa时5个通道中的努森数分别为12.82、8.55、6.41、5.13和4.27,此时有kapp≈6kintrinsicKn=λH/2,多孔介质表观渗透率对孔隙尺寸的敏感性减弱,流速与孔隙尺寸呈线性函数关系。由此可见不同压力下裂缝对致密多孔介质中气体渗流影响的不同由努森数引起,对于致密多孔介质,在高压下努森数较小,孔隙尺寸较大的微裂缝提高致密介质渗透率的作用更明显;而在低压下努森数较大,微裂缝提高致密介质渗透率的作用相对较弱,这就是产生图5(b)的原因。对于油在多孔介质中的流动或常规孔隙中的气体流动,由于其对应的努森数都较小,因而不同压力下裂缝对渗流的影响基本一致,不会表现出裂缝性致密多孔介质中气体渗流的特点。

4 结 论

(1)微裂缝的存在能够明显提高致密多孔介质的渗透率;随着压力增加,微裂缝提高致密介质气体渗透率的作用增强,且连通性裂缝的影响更明显;并且当压力极大或极小时,微裂缝的影响趋于稳定。

(2)随着压力减小,基岩与裂缝中的流速差别减小,基岩对多孔介质中流量的贡献增加;且当压力极大或极小时,裂缝与基岩中平均流速比也趋于定值。

(3)对于致密多孔介质,当压力很高时努森数很小,多孔介质渗透率与孔隙尺寸呈二次函数关系,渗透率对孔隙尺寸敏感;而当压力很低时努森数很大,多孔介质渗透率与孔隙尺寸呈线性函数关系,渗透率对孔隙尺寸的敏感性减弱,揭示了在高压下尺寸较大的微裂缝提高致密介质渗透率的作用更强的原因。

[1] 贾承造,郑民,张永峰.中国非常规油气资源与勘探开发前景[J].石油勘探与开发,2012,39(2):129-136.

JIA Chengzao, ZHENG Min, ZHANG Yongfeng. Unconventional hydrocarbon resources in China and the prospect of exploration and development [J]. Petroleum Exploration and Development, 2012,39(2):129-136.

[2] 姚军,孙海,黄朝琴,等.页岩气藏开发中的关键力学问题[J].中国科学(物理学 力学 天文学),2013,43(12):1527-1547.

YAO Jun, SUN Hai, HUANG Zhaoqin, et al. Key mechanical problems in the developmentof shale gas reservoirs [J]. Scientia Sinica Physica, Mechanica & Astronomica, 2013,43(12):1527-1547.

[3] 邹才能,董大忠,王社教,等.中国页岩气形成机理,地质特征及资源潜力[J].石油勘探与开发,2010,37(6):641-653.

ZOU Caineng, DONG Dazhong, WANG Shejiao, et al. Geological characteristics, formation mechanism and resource potential of shale gas in China [J]. Petroleum Exploration and Development, 2010,37(6):641-653.

[4] 邹才能,朱如凯,吴松涛,等.常规与非常规油气聚集类型,特征,机理及展望:以中国致密油和致密气为例[J].石油学报,2012,33(2):173-187.

ZOU Caineng, ZHU Rukai, WU Songtao, et al. Types,characteristics,genesis and prospects of conventional and unconventional hydrocarbon accumulations:taking tight oil and tight gas in China as an instance [J]. Acta Petrolei Sinica, 2012,33(2):173-187.

[5] JAVADPOUR F, FISHER D, UNSWORTH M. Nanoscale gas flow in shale gas sediments[J]. Journal of Canadian Petroleum Technology, 2007,46(10):55-61.

[6] 杨峰,宁正福,胡昌蓬,等.页岩储层微观孔隙结构特征[J].石油学报,2013,34(2):301-311.

YANG Feng, NING Zhengfu, HU Changpeng, et al. Characterization of microscopic pore structures in shale reservoirs[J]. Acta Petrolei Sinica, 2013, 34(2):301-311.

[7] KUUSKRAA V, STEVENS S H, MOODHE K D. Technically recoverable shale oil and shale gas resources: an assessment of 137 shale formations in 41 countries outside the United States[M]. Washington: Independent Statistics & Analysis and US Department of Energy, 2013.

[8] ZHANG M, YAO J, SUN H, et al. Triple-continuum modeling of shale gas reservoirs considering the effect of kerogen[J]. Journal of Natural Gas Science and Engineering, 2015,24:252-263.

[9] YAO J, SUN H, FAN D Y, et al. Numerical simulation of gas transport mechanisms in tight shale gas reservoirs[J]. Petroleum Science, 2013,10(4):528-537.

[10] ROY S, RAJU R, CHUANG H F, et al. Modeling gas flow through microchannels and nanopores[J]. Journal of Applied Physics, 2003,93(8):4870-4879.

[11] KOPLIK J, BANAVAR J R. Continuum deductions from molecular hydrodynamics[J]. Annual Review of Fluid Mechanics, 1995,27(1):257-292.

[12] SHAN X, YUAN X F, CHEN H. Kinetic theory representation of hydrodynamics: a way beyond the Navier—Stokes equation[J]. Journal of Fluid Mechanics, 2006,550:413-441.

[13] FATHI E, AKKUTLU I Y. Lattice Boltzmann method for simulation of shale gas transport in kerogen[J]. SPE Journal, 2012,18(1):27-37.

[14] ZHANG X, XIAO L, SHAN X, et al. Lattice Boltzmann simulation of shale gas transport in organic nano-pores[J/OL]. Scientific Reports, 2014, 4: 4843. [2016-12-01]. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4007072/.

[15] 宁正福,王波,杨峰,等.页岩储集层微观渗流的微尺度效应[J].石油勘探与开发,2014,41(4):445-452.

NING Zhengfu, WANG Bo, YANG Feng, et al. Microscale effect of microvadose in shale reservoirs[J]. Petroleum Exploration and Development, 2014,41(4):445-452.

[16] 姚军,赵建林,张敏,等.基于格子Boltzmann方法的页岩气微观流动模拟[J].石油学报,2015,36(10):1280-1289.

YAO Jun, ZHAO Jianlin, ZHANG Min, et al. Microscale shale gas flow simulation based on lattice boltzmann method[J]. Acta Petrolei Sinica, 2015,36(10):1280-1289.

[17] 张磊,姚军,孙海,等.利用格子Boltzmann方法计算页岩渗透率[J].中国石油大学学报(自然科学版),2014,38(1):87-91.

ZHANG Lei, YAO Jun, SUN Hai, et al. Permeability calculation in shale using lattice Boltzmann method[J]. Journal of China University of Petroleum(Edition of Natural Science), 2014,38(1):87-91.

[18] 孙海,姚军,张磊,等.基于孔隙结构的页岩渗透率计算方法[J].中国石油大学学报(自然科学版),2014,38(2):92-98.

SUN Hai, YAO Jun, ZHANG Lei, et al. A computing method of shale permeability based on pore structures[J]. Journal of China University of Petroleum(Edition of Natural Science), 2014,38(2):92-98.

[19] ZHAO J, YAO J, LI A, et al. Simulation of microscale gas flow in heterogeneous porous media based on the lattice Boltzmann method[J]. Journal of Applied Physics, 2016,120(8):084306.

[20] ZHAO J, YAO J, ZHANG M, et al. Study of gas flow characteristics in tight porous media with a microscale lattice Boltzmann model[J/OL]. Scientific Reports, 2016,6:32393. [2016-12-01].https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5009359/.

[21] 张磊,姚军,孙海,等.基于数字岩心技术的气体解析/扩散格子Boltzmann模拟[J].石油学报,2015,36(3):361-365.

ZHANG Lei, YAO Jun, SUN Hai, et al. Lattice Boltzmann simulation of gas desorption and diffusion based on digital core technology[J]. Acta Petrolei Sinica, 2015,36(3):361-365.

[22] ZHAO J, YAO J, ZHANG L, et al. Porescale simulation of shale gas production considering the adsorption effect[J]. International Journal of Heat & Mass Transfer, 2016,103:1098-1107.

[23] ZHANG L, KANG Q, YAO J, et al. Pore scale simulation of liquid and gas two-phase flow based on digital core technology[J]. Science China Technological Sciences, 2015,58(8):1375-1384.

[24] CHEN L, FANG W, KANG Q, et al. Generalized lattice Boltzmann model for flow through tight porous media with Klinkenbergs effect[J]. Physical Review E, 2015,91(3):033004.

[25] ZHANG Y H, GU X J, BARBER R W, et al. Capturing Knudsen layer phenomena using a lattice Boltzmann model[J]. Physical Review E, 2006,74(4):046704.

[26] SUGA K, TAKENAKA S, ITO T, et al. Evaluation of a lattice Boltzmann method in a complex nanoflow[J]. Physical Review E, 2010,82(1):016701.

[27] SHAN X, CHEN H. Lattice Boltzmann model for simulating flows with multiple phases and components[J]. Physical Review E, 1993,47(3):1815.

[28] REN J, GUO P, GUO Z, et al. A lattice Boltzmann model for simulating gas flow in kerogen pores[J]. Transport in Porous Media, 2015,106(2):285-301.

[29] LI Q, HE Y, TANG G, et al. Lattice Boltzmann modeling of microchannel flows in the transition flow regime[J]. Microfluidics and Nanofluidics, 2011,10(3):607-618.

[30] ANSUMALI S, KARLIN I V. Kinetic boundary conditions in the lattice Boltzmann method[J]. Physical Review E, 2002,66(2):026311.

[31] TANG G, TAO W, HE Y. Lattice Boltzmann method for gaseous microflows using kinetic theory boundary conditions[J]. Physics of Fluids, 2005,17(5):058101.

[32] ZHANG R, SHAN X, CHEN H. Efficient kinetic method for fluid simulation beyond the Navier-Stokes equation[J]. Physical Review E, 2006,74(4):046703.

[33] SUGA K. Lattice Boltzmann methods for complex micro-flows: applicability and limitations for practical applications[J]. Fluid Dynamics Research, 2013,45(3):034501.

[34] KLINKENBERG L. The permeability of porous media to liquids and gases: proceedings of the Drilling and Production Practice[C]. American Petroleum Institute, 1941.

[35] CHALMERS G R, BUSTIN R M, POWER I M. Characterization of gas shale pore systems by porosimetry, pycnometry, surface area, and field emission scanning electron microscopy/transmission electron microscopy image analyses: examples from the Barnett, Woodford, Haynesville, Marcellus, and Doig units[J]. AAPG bulletin. 2012,96(6):1099-1119.