工程项目进度风险因素叠加性影响研究
2018-03-15黎恒杆陈金雄苏俊贤王中豪
黎恒杆,陈金雄,苏俊贤,王中豪,姜 昆
(1.武夷学院 土木工程与建筑学院, 福建 武夷山 354300;2.武夷学院 数学与计算机学院,福建 武夷山 354300)
1 引言
工程建设项目通常具有投资大、建设周期长及影响因素多的特点,因此对工程建设项目进行有效的控制和风险管理是影响工程建设项目成败的关键。工程建设项目控制的要素很多,如目标、进度、成本、质量、安全等。由于工程进度的显性特征,其还往往会影响到其他控制要素,因此在工程建设项目中进度控制是关键的,倘若项目的进度失控,它不仅会影响其他目标,还将导致项目资源的巨大浪费。实践和理论都表明影响工程建设项目进度风险的因素很多,如表1所示。

表1 影响工程项目进度风险因素及其体现Table 1 Risk factors and its embodiments effecting schedule management on project
这些风险因素来自多层次、多方面,有的是容易度量(或可预知),有的则不容易度量(或不可预知),它们之间还会相互作用影响(即风险的叠加性)。从工程建设项目风险因素的叠加性影响进行研究,期待在大量实际工程建设项目数据分析基础上,利用贝叶斯网络建立分析模型,比较风险因素的叠加和非叠加的影响。
国内外研究者关于工程建设项目进度风险的研究并不少见,基本是利用数学模型(如层次分析法、模糊数学法、网络分析法、蒙特卡法、粗集神经网络法、贝叶斯网络)进行研究,很好的丰富和完善了工程建设项目风险管理研究领域。欧阳焜[1]对BIM技术下项目工程的相关概念、影响因素和保障措施进行研究,建立多因素随机性工程项目进度预测模型。武民民[2]通过比较矩阵法和专家经验法分别确定了工程进度影响因子的权重值,为确定2种方法获得的权重值中的较优者,采用遗传算法,应用MATLAB软件对问题进行了模拟仿真。田耐[3]提出一种环境因素对桥梁建造工程进度管理影响的建模方案,在环境因素建模分析的基础上,引进了EECR技术,能够准确的评估环境因素对桥梁建造工程管理过程的影响程度。武菲菲等[4]从分析影响项目工期的风险因素出发,对每一风险因素所引起的项目作业拖延时间根据其特征可以给出不同的假设分布,确定各风险因素对作业的影响,并通过蒙特卡罗模拟确定项目各路径工期的分布。黄建文等[5]针对传统计划评审技术在计算完工概率时假设条件的局限性(假设条件与工程实际存在偏差,导致完工概率偏大),提出了基于贝叶斯网络的施工进度完工概率分析方法。项勇[6]在贝叶斯网络图的理念下,引入非叠加性原理,探讨多个风险因素共同作用的影响。Steven Doskey[7]等用贝叶斯网络度量系统工程,用以鉴别和分析系统工程的模式和预测可以的风险,并把它发展成为一个复杂的信息系统;Lee等[8]用贝叶斯网络对大工程进行风险管理,并把它应用于韩国的造船工业中。刘俊艳、王卓甫[9]采用贝叶斯网络方法验证风险因素同时发生时产生的影响是否等于各风险因素单独作用下所产生的影响之和。
从上述文献可看出国内对工程建设项目进度风险因素的研究大量运用了各种数学理论方法,但未能就风险因素的独立性和叠加影响进行对比分析。在实际的工程建设项目活动中,必然同时存在多个风险因素影响。对于这些风险因素之间的关系和对控制目标所产生影响的叠加性和非叠加性研究,无论是工程界还是学术界均较为少见,而这种综合的影响对项目管理者所作出的决策、规划都非常重要。因此本文拟在调查大量的工程建设项目案例数据基础上,利用贝叶斯网络方法分析工程建设项目风险因素的叠加性和非叠加性影响。
2 基于贝叶斯网络的风险因素模型建立
2.1 贝叶斯网络模型
贝叶斯网络是一个带有概率的有向无环图,这个图模型能够表示变量集合的联合概率分布,可以分析大量变量之间的相互关系,利用贝叶斯定理的学习和统计推断功能实现预测、诊断、分类等任务[10]。它是联合概率分布的分解是一种表示,即,假设网络中的变量为,假设给定中其它变量条件独立,那么联合概率分布为:
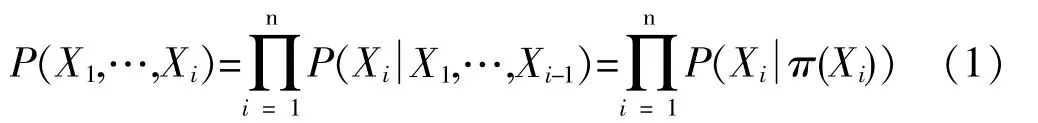
公式(1),其中当 π(Xi)=θ时,即是边缘分布 P(Xi)。
利用贝叶斯网络可以容易求解节点的后验概率,先验概率和后验概率是相对于某组数据而言的。设X,Y为两个随机变量,X=x为某一假设,Y=y为一组数据,在考虑数据Y=y之前,对事件X=x的概率估计P(X=x)成为先验概率。而在考虑数据之后,对X=x的概率估计成为后验概率。贝叶斯定理给出了先验概率及后验概率之间的关系,即贝叶斯公式:
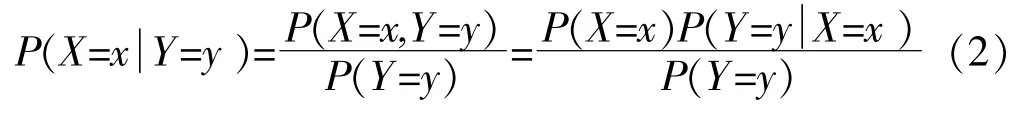
公式(2),式中 P(X=x,Y=y)是 X=x∧Y=y 的联合概率;P(X=x)为先验概率;是A的后验概率,且如果X、Y独立,则;为A的联合概率。
2.2 模型的建立
选择贝叶斯网络模型进行工程项目进度风险因素的叠加和非叠加性分析,可以分析到某项作业内容是受到何种风险因素及作用程度的影响,同时可以计算这些风险因素对工期变化的影响概率。在利用贝叶斯网络分析时须了解各种风险因素的效率以及工程项目所处的运行状态,这些数据可以通过收集实际工程项目运行资料统计得到。具体利用贝叶斯网络进行工程进度分析的步骤如下:
(1)通过实际工程项目运行资料的统计,选择影响工程进度较为明显的风险因素;
(2)建立工程进度风险贝叶斯网络,把工程项目的网络图用贝叶斯网络形式表现;贝叶斯网络中各节点即为各工程活动,网络箭头表示工程活动间的逻辑关系;再将风险因素加入工程进度贝叶斯网络中构成了工程项目进度风险贝叶斯网络;
(3)利用贝叶斯公式计算受多个风险因素影响下的工程活动进度风险;
(4)利用贝叶斯公式逐一分别计算第三步风险因素单独作用下的工程活动进度风险;
(5)比较第3、4步计算结果,分析验证风险因素是否存在非叠加影响。
3 实例分析
在工程项目实践中可以显而易见的感知到项目的运行往往处于某一种状态(定义这些状态为好、中、差),在不同的状态下各进度风险影响因素的效率是不一样的,为了验证贝叶斯网络模型的有效性和精度,收集了本地近五年的工程建设项目资料,通过专家评估法得到因素状态和效率概率的先验概率分别为好(0.64)、中(0.22)、差(0.14)和高(0.82)、低(0.18);其余数据如表2所示。
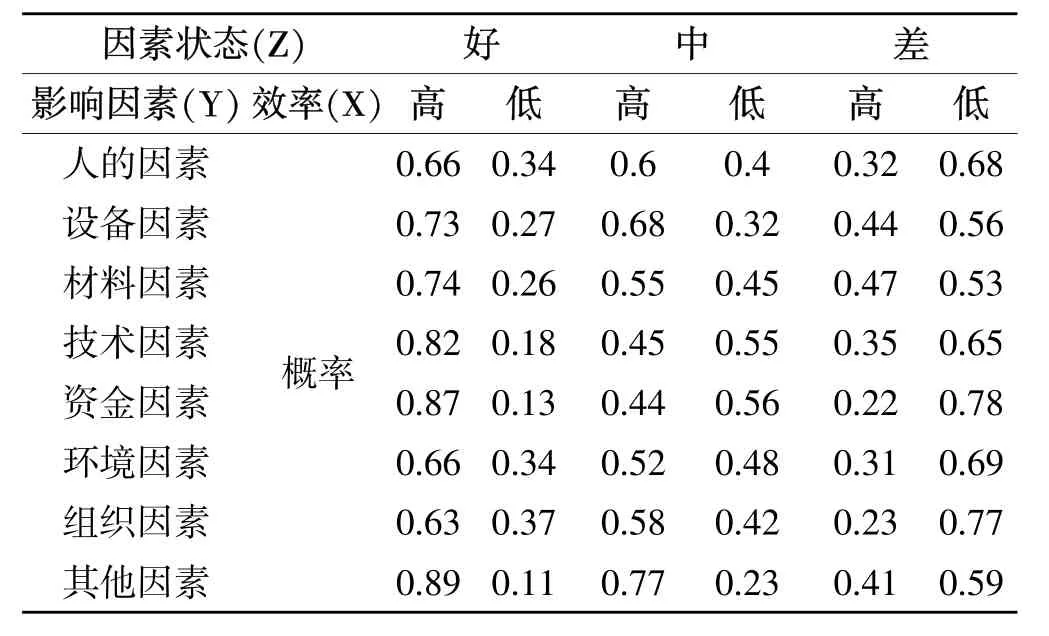
表2 项目进度风险因素状态、效率及概率表Table 2 Status,efficiency and probability of schedule management on project
3.1 计算工程项目进度的后验概率
由公式(2)计算得工程进度各影响因素的后验概率如表3所示。

表3 影响因素后验概率表Table 3 Posterior probability of effect factors
3.2 叠加性影响分析
(1)假设某时段因素状态为“中”,即 P(Z=好)=0,P(Z=中)=0.86,P(Z=差)=0.14,而效率不变,根据贝叶斯公式此时的进度因素风险概率如表4所示。

表4 (1)状态下的影响因素风险概率表Table 4 Risk probability of effect factor under condition 1
(2)假设某时段因素状态为“差”,即 P(Z=好)=0,P(Z=中)=0.22,P(Z=差)=0.78,而效率不变,根据贝叶斯公式此时的进度因素风险概率如表5所示。
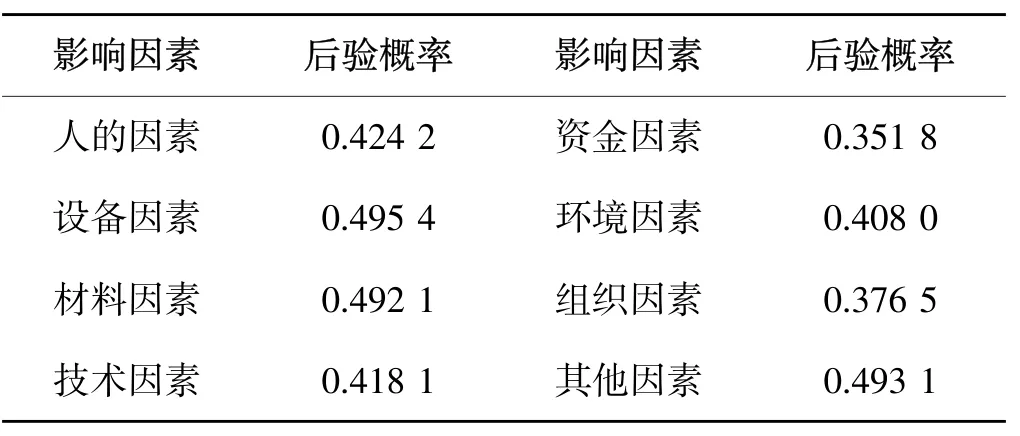
表5 (2)状态下的影响因素风险概率表Table 5 Risk probability of effect factor under condition 2
(3)假设某时段效率为“低”,即 P(X=低)=1, P(X=高)=0,而因素状态不变,根据贝叶斯公式此时的进度因素风险概率如表6所示。

表6 (3)状态下的影响因素风险概率表Table 6 Risk probability of effect factor under condition 3
(4)假设某时段效率为“低”,即 P(X=低)=1,P(X=高)=0,而因素状态为“中”,即 P(Z=好)=0,P(Z=中)=0.86,P(Z=差)=0.14,根据贝叶斯公式此时的进度因素风险概率如表7所示。

表7 (4)状态下的影响因素风险概率表Table 7 Risk probability of effect factor under condition 4
(5)假设某时段效率为“低”,即 P(X=低)=1, P(X=高)=0,而因素状态为“差”,即 P(Z=好)=0,P(Z=中)=0.22,P(Z=差)=0.78,根据贝叶斯公式此时的进度因素风险概率如表8所示。
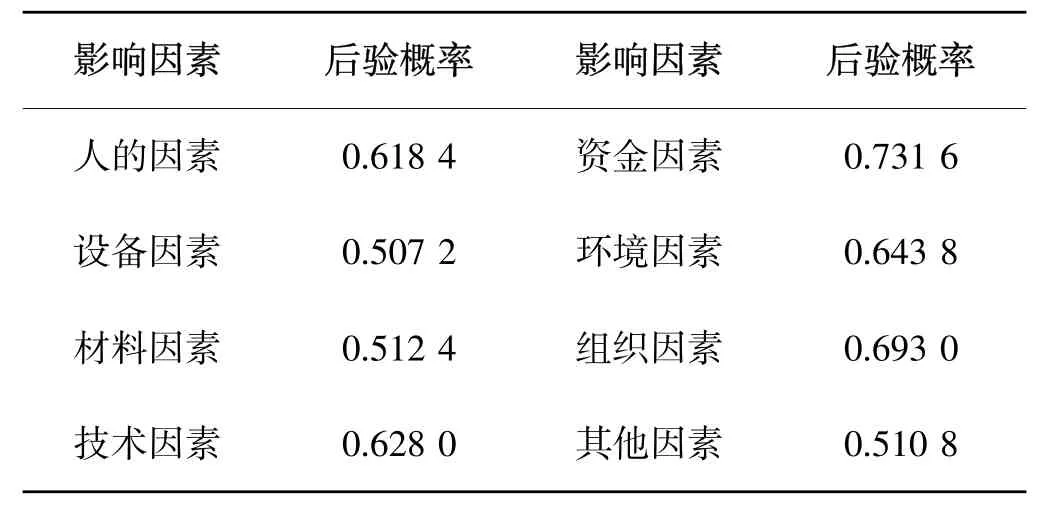
表8 (5)状态下的影响因素风险概率表Table 8 Risk probability of effect factor under condition 5
综合比较上述(1)-(5)的5种情形,当因素状态和效率分别或同时处于劣势时,工程进度风险与最初的计算相比较发生了相应的变化,如表9所示。
由表9可知,当因素状态为中、效率为差时,他们所引起的进度风险的变化量之和为-0.166 3,不等于当因素状态和效率同时处于劣势时所引起的进度风险变化量-0.113 8。此时,单个因素分别发生引起的进度风险之和是多个因素同时恶化产生的影响的1.461 3倍;当因素状态为差、效率为差时,他们所引起的进度风险的变化量之和为-0.281 0,不等于当因素状态和效率同时处于劣势时所引起的进度风险变化量0.065 4。此时,单个因素分别发生引起的进度风险之和是多个因素同时恶化产生的影响的-4.296 6倍。
(6)假设某时段因素状态为“好”,即 P(Z=好)=1,P(Z=中)=0,P(Z=差)=0,而效率不变,此时的进度风险为,根据贝叶斯公式此时的进度因素风险概率如表10所示。

表9 (1)-(5)状态下各因素叠加性影响分析表Table 9 Analysis of superposition effects of factors under conditions from 1 to 5
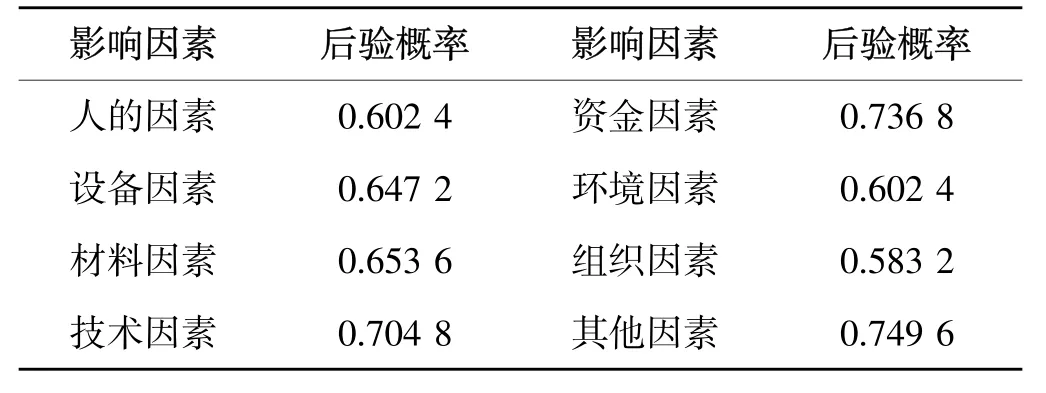
表10 (6)状态下的影响因素风险概率表Table 10 Risk probability of effect factor under condition 6
(7)假设某时段效率为“高”,即 P(X=低)=1, P(X=高)=0,而因素状态不变,此时的进度风险为,根据贝叶斯公式此时的进度因素风险概率如表11所示。
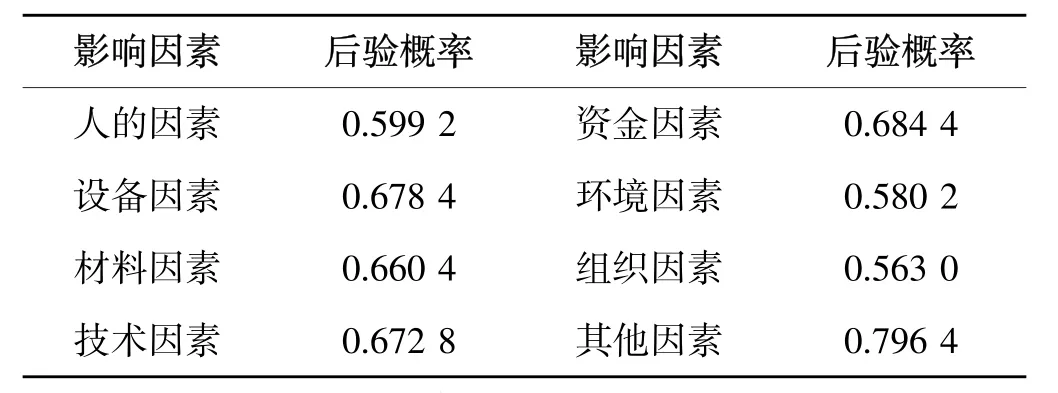
表11 (7)状态下的影响因素风险概率表Table 11 Risk probability of effect factor under condition 7
(8)假设某时段因素状态为“好”,即 P(Z=好)=1,P(Z=中)=0,P(Z=差)=0,效率为“高”,即 P(X=低)=1, P(X=高)=0,此时的进度风险为,此时的进度风险为,根据贝叶斯公式此时的进度因素风险概率如表12所示。
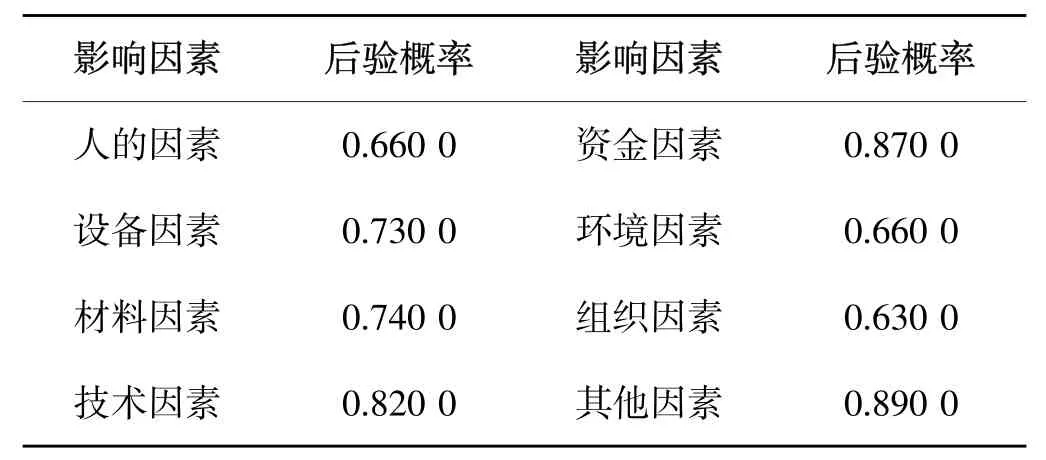
表12 (8)状态下的影响因素风险概率表Table 12 Risk probability of effect factor under condition 8
综合比较上述(6)-(8)的3种情形,当因素状态和效率分别或同时处于优势时,工程进度风险与最初的计算相比较发生了相应的变化,如表13所示。

表13 (6)-(8)状态下各因素叠加性影响分析表Table 13 Analysis of superposition effects of factors under conditions from 6 to 8
由表13可知,当因素状态为好、效率为高时,他们所引起的进度风险的变化量之和为0.095 6,不等于当因素状态和效率同时处于优势时所引起的进度风险变化量0.107 0。此时,单个因素分别发生引起的进度风险之和是多个因素同时恶化产生的影响的0.893 5倍。
4 结论
本文利用贝叶斯网络分析了在工程项目中,影响工程进度风险的各因素在不同状态下对工程进度的非叠加性影响的情况。通过案例计算说明得出结论:
(1)对影响工程项目进度风险因素进行分析研究,表明多个风险因素作用下产生的工程项目进度风险为非叠加性,且非叠加性影响的大小视项目管理的效率、风险因素的状态而定。
(2)本模型利用贝叶斯网络分析了在工程项目中,影响工程进度风险的各因素在不同状态下对工程进度的非叠加性影响的情况。由于不同组合及不同组合节点状态产生的非叠加性影响大小不同,而又不可能尽数各种风险因素及组合,故何种状况非叠加性影响大于叠加和,何种状况非叠加性影响小于叠加和尚不能确定。
(3)各风险因素之间的相互作用影响的原因还有待进一步研究分析,文中只做了三种因素的叠加研究,在某些极端情况下所有因素的叠加情况还需进一步研究。
