学业考试命题之思考

□ 海南华侨中学 李红庆

□ 湖北省天门中学 刘国华

□ 海口景山学校 陈元林

以《课标》视角审视学业考试命题，应该根据学生的年龄特征、思维特点、考试性质、数学背景和生活经验编制试题，面向全体学生，使具有不同认知特点、不同数学发展程度都能表现自己的学习状态。学业考试要求公正、客观、全面、准确地反映学生通过初中的数学学习所获得的发展状况。基于此，本文拟从考试的性质、考学和考教关系谈几点思考：

学业考试的性质

学业考试命题要体现义务教育普及性、基础性和发展性，同时还要兼顾高中招生考试的选拔性、公正性和基础教育的衔接性。普及性是适龄儿童和青少年必须接受教育，根据法律赋予的权力，国家、社会、家庭必须予以保证的国民教育，义务阶段数学教育是国民教育的其中一部分，命题题源应该取材于义务教育教材，并稍活于教材，命题能体现每个受教育者都知道的内容，并且作为国民必须具备基础知识；基础性是指学生在义务教育阶段所学数学教育是基础知识，不要求学得很专业，但要求内容都了解，即为人的一生发展夯实基础的数学教育；发展性是指学生现有发展水平和潜在发展可能性，既要体现发展结果，更要体现发展过程，即学业考试要体现发展性评估功能。由于学业考试又作为高中招生考试，必须具备选拔性，选拔性要体现一定的信度、效度、区分度、灵活度和适当的难度，只有这样才能既对一切学生公正，又对较优秀学生也公正。由于社会发展，人们对子女的学历期望值的提高，经过学业考试的学生多数要进行高中继续接受基础教育，因此，学业考试也要考虑初高中数学的衔接性，为高中数学教育铺垫好基础。下面依学业考试的性质审视下列试题：

案例1：（图形与空间中关于角计算一组题组）

题1.（2017四川省内江市学业考试第4题）如图1-（1），直线m∥n，直角三角板ABC的顶点A在直线m上，则∠a的余角等于（）。

A．19° B．38° C．42° D.52°

题2.（2017年安徽省学业考试第6题）如图1-（2），直角三角板和直尺如图放置，则∠2的度数为（ ）。

A．60° B． 50° C． 40° D．30°

（1）加强喷混材料的选配研究。喷混材料的选择配置是喷混植生技术的核心。研发的主体是粘结剂、有机物质、保水材料、pH缓冲剂等的筛选；乔、灌、草种的选择和配置；不同生态型（例如以灌木为主的灌草生态植被型，以草为主的草灌生态植被型等）的种子喷播技术。

题3. （2016年海南省学业考试第13题）如图1-（3）， 矩形ABCD的顶点A，C分别在直线a，b上，且a∥b，∠1＝60°，则∠2的度数为（ ）

A．30° B．45° C．60° D． 75°

题4. （2017年河北省学业考试第18题）如图1-（4），依据尺规作图的痕迹，计算∠a＝ 。

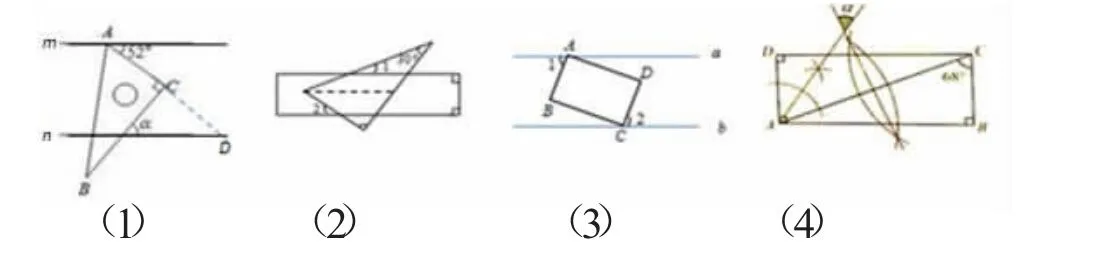
图1

解析：对于题1：只须过延长AC交直线n于点D，即知∠a＋50°＝90°；对于题 2：过三角板 60°的顶点作直尺的平行线，即得 90°－∠2＝∠1＋30°；对于题 3：命题者本意想考查等角定理或对称旋转知识，用心在设计试题，但学生根本不会想什么定理和对称旋转知识，而直接通过观察即可得到∠2的度数，是一道无效的明视题；对于题4：由作图痕迹发现其中∠a的一条边是线段AC的中垂直线，再由作图痕迹∠a的另一条边是∠CAD的平分线，由互余关系得∠a＝90°－×68°＝56°。

点评：依学业考试性质审视这4道题，应该说题1、题2命制比较好，能体现普及性、基础性、发展性、选拔性和衔接性．题3是个无效题的明视题，根本没有考什么内容，尽管命题者煞费苦心在用心设计试题，但学生不需要任何学习都能选出正确选项，对多数学生是不公正的！题4的普及性稍为欠失一点，但基础性、发展性、选拔性及初高中数学思想方法的衔接性很强，并且它注意考查基础知识和基本活动经验，尤其是基本体验对未来高中数学的学习起到了比较好的衔接作用。

学业考试要考查“四基”

《课标》明确规定了初中数学课程目标要“适应学生终身学习”，既要有“基础知识、基本技能”，又要有“基本思想、基本活动经验”，考虑到经过学业考试的学生大多数都会升入高中继续接受基础教育，学业考试命题要兼顾既考查传统“双基”，又考查新增“双基”，由于学业考试还具有初中教学“指挥棒”的作用，所以，学业考试命题还兼顾着落实《义务课标》中规定的初中数学的课程目标和课程内容。因此，学业考试命题还需要课程目标的“四基”来审视。下面依课程目标的“四基”审视下列试题：

案例2：

题1：（2015年海南省学业考试第18题））如图2-（1），矩形 ABCD 中，AB＝4，BC＝4，则图中 4 个小正方形的周长之和为 ______________。

题2：（2017年河北省学业考试第25题）平面内，如图 2-（2），在平行四边形 ABCD 中，AB＝10，AD＝15，tanA＝。点P为AD边上任意一点，连接PB，将绕点P逆时针旋转90°得到线段PQ。

（1）当∠DPQ＝10°时，求∠APB 的大小；

（2）当 tan∠ABP：tanA＝3：2 时，求点 Q 与点 B间的距离（结果保留根号）；

（3）若点Q恰好落在平行四边形ABCD的边所在的直线上，直接写出PB旋转到PQ所扫过的面积（结果保留π）。

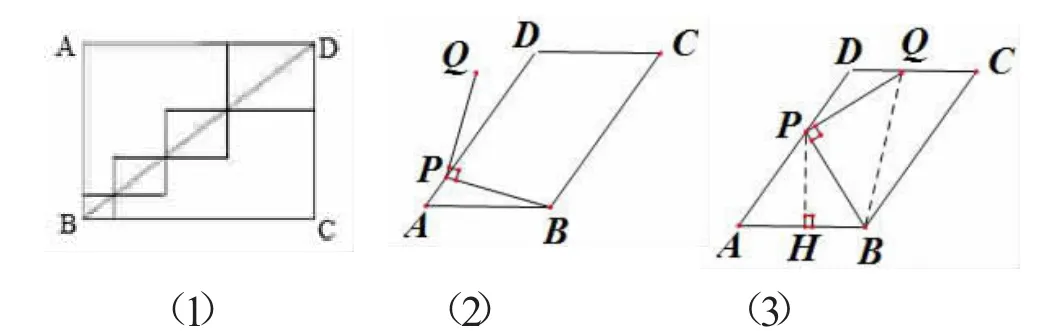
图2

点评：对于题1：既考查勾股定理又考查图形变换的图形的平移问题，找到每个矩形的对角线与边的关系，还考查了归纳和整体思想，同时也能考查基本活动经验．这个题设计较简单，但考查效果好。

对于题2（1）：分线段PD在∠BPQ内和外两种情形讨论，由直角和平角的定义，分别得∠ABP＝100°或80°，考查了分类讨论思想和基本活动经验。

题 2（2）：如图 2-（3），过点 P 作 PH⊥AB 于点 H，

题 2（3）：①若点 Q 在直线 AD 上时，如图 3-（1），在Rt△APB中，由tanA＝，AB＝10，知 PB＝8，扫过的扇形BPQ的面积为

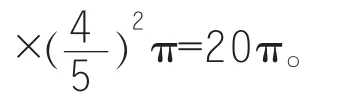
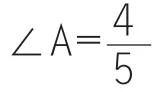
图3

题2（3）问，对基础知识和基本技能，基本思想和基本活动经验的考查可以说是淋漓尽致，完全符合《课标》的要求。