NAO机器人手臂的运动建模与控制

温盛军， 翟 睿， 郭光复， 康连启， 朱 菁

(中原工学院 中原彼得堡航空学院， 河南 郑州 450007)

具有多个自由度的关节式机器人，已成为机器人技术和人工智能的研究热点。目前，许多研究人员已经对机器人运动学、动力学建模及智能控制进行了深入的研究：Kofinas N等将NAO机器人分解成五个独立的部分(头、左右手臂和左右腿)，利用D-H法和非线性方程的解析解，得出了NAO机器人完整的正逆运动学的解析解[1]；姜静等基于假设模态法结合Lagrange方程建立了刚-柔性耦合机械臂的动力学方程。研究的PID控制器因简单、有效、实用而被普遍地应用于机械臂控制[2]；金国光等用PID和PD两种控制方法对机械臂轨迹进行跟踪对比发现，在重力补偿的情况下，PD控制算法是全局渐进稳定的[3]；Kelly R提出了带有非线性位置误差函数积分的线性PD反馈方法，得到了确保全局渐进稳定性调节的明确条件[4]。

对于NAO机器人来说，其手臂结构比较复杂，独立的PD控制不能满足手臂运动的控制精度、鲁棒性和稳定性要求，因此，需在PD控制的基础上采用鲁棒自适应PD控制。自适应控制能在参数变化时自动地对系统进行调节，使系统随时处于最佳状态，进而使NAO机器人手臂的运动达到控制要求。

本文在上述理论和研究的基础上，利用D-H方法建立NAO机器人手臂运动学模型，进而根据Lagrange方程得出动力学模型，采用PD控制策略以及自适应PD控制策略对机器人手臂的定点控制进行研究，最后给出MATLAB仿真。

1 NAO机器人手臂运动建模

以Aldebaran Robotics公司于2012年研发的一款NAO H25型V5版本机器人作为平台来研究机器人的手臂控制。它身高57 cm，重5.4 kg，可以在多种平台上编程(如Linux、Windows或Mac OS等)，并且拥有开放式的编程构架。

1.1 NAO机器人手臂结构分析

机器人全身有25个自由度，动作灵活，可完成各种仿人动作。此外它还拥有一个惯性导航仪装置，该装置一系列的传感器可以保证它的活动十分准确，并让NAO机器人更好地保持平衡。

NAO机器人手臂有5个自由度，肩膀处有俯仰和横滚2个自由度，肘部有偏转和横滚2个自由度，腕部有偏转1个自由度。其中，Pitch表示俯仰，绕x轴旋转；Yaw表示偏转，绕y轴旋转；Roll表示横滚，绕z轴旋转，其左臂结构图如图1所示。

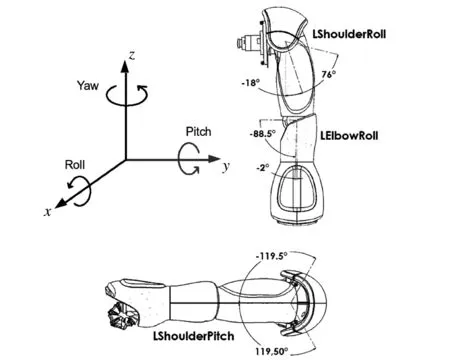
图1 NAO机器人左臂结构图

1.2 NAO机器人手臂运动学模型

对于一个机器人的机械臂，运动学描述的是关节位置与末端执行器位置和方向之间的解析关系，包括机械臂的位置、速度和加速度以及它们相对于时间的导数，不需考虑使机械臂产生运动的力、力矩[5]。机械臂的运动学包括正运动学和逆运动学。机械臂正运动学描述的是已知机械臂关节的角度值，用来计算机械臂末端位姿，对于正运动学，它的解是唯一确定的，即各个关节变量给定之后，机械臂的末端位姿是唯一确定的。

D-H是描述机械臂结构运动参数的经典运动学模型，其变换矩阵由α，a，θ，d这4个参数来描述。从坐标系i到坐标系i-1的变换矩阵是一个只与关节变量qi有关的函数，通过以下齐次变换矩阵来构建正运动学方程。

(1)

NAO机器人手臂运动的总齐次变换矩阵T为

(2)

肘部和腕部两个关节绕y轴旋转方式只影响机械臂末端的位姿，而对机械臂在三维空间的位置并不产生影响，所以忽略这两个旋转关节，肩膀绕z轴旋转在本研究中不考虑。由此可以得到NAO机器人左手臂的运动学D-H参数见表1。

表1 NAO左臂运动学D-H参数

根据以上运动学D-H模型参数求NAO机器人手臂运动学正解，获得在关节空间中NAO手臂末端的位置与各个关节角度大小之间的关系。令c表示cos，s表示sin，手臂正运动学方程为

(3)

则机器人手臂末端位置为

(4)

1.3 NAO机器人手臂运动学模型验证

经过软件交叉编译后，可直接使用C++对NAO机器人进行编程。通过编程，使NAO机器人左手臂由自然下垂状态摆至LShoulderPitch为1弧度，LElbowRoll为-1弧度的状态，NAO机器人手臂摆起位姿如图2所示。

图2 NAO机器人手臂摆起位姿

使用Robotics Toolbox在MATLAB上对NAO机器人手臂运行学模型进行仿真实验。Robotics Toolbox是由科学家Peter Corke设计的，它提供了诸多功能函数模块，如轨迹生成模块、运动学模块、动力学模块等，极大地方便了人们对机器人的研究[7]。

用计算机对NAO机器人手臂运动学模型进行仿真，首先要构建相应的对象，在构建关节时，会用到Link函数，其一般形式为：

L=Link([angle1Aangle2Dangle3])

(5)

其中：angle1代表扭转角；A代表连杆长度;angle2代表关节角；D代表偏距；angle3代表关节类型，其为0代表旋转关节，其为1代表平动关节。

根据NAO机器人左臂两关节的D-H参数，在MATLAB上利用Robotics Toolbox创建一个简单的两关节机器人模型。本文对NAO机器人手臂进行定点控制，设起始位置q0=[1.474 13 -0.417 206]，为机器人站立时手臂自然垂下时的位置。设目标位置q1=[1.0 -1.0]，采样时间t=[0:0.05:1]。仿真结果与NAO机器人手臂运动采集的数据对比如图3所示。

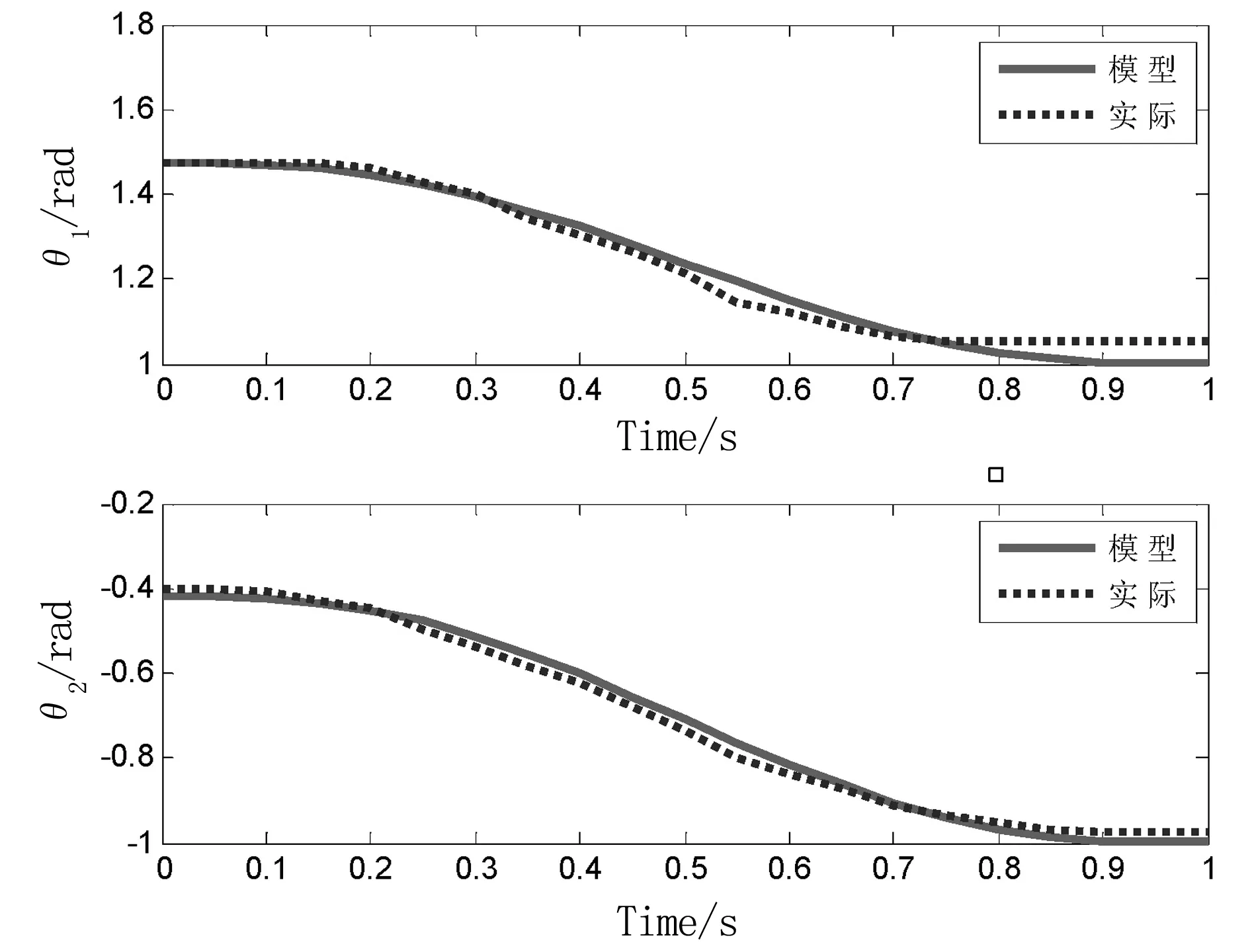
图3 模型与实际关节角变化对比结果

从图3可以看出，机器人手臂两个关节角度的MATLAB仿真变化曲线与实际NAO机器人手臂的运动轨迹基本一致，这表明通过D-H法所建立的NAO机器人手臂运动学模型是正确的。因此，可以依据此模型继续进行动力学建模和控制器设计。

1.4 NAO机器人手臂动力学模型

对于任何一个控制系统来说，要想对这个系统进行控制，就必须建立与其相对应的被控对象的数学模型。常规的机械臂由很多关节组成，是一个具有强耦合性的复杂系统，其动力学方程是非线性的，而且随着自由度的增大其动力学方程会越来越复杂。研究机器人的动力学问题，主要就是研究如何解决对机器人控制的问题。

在运动学的基础上，获得机械臂各关节上所需驱动力、力矩与机械臂运动之间的关系，是机械臂动力学研究的主要内容。动力学方程是机械臂力学控制方面的基础，因而可通过使用动力学方程来实现对机械臂运动的控制[6]。

研究机械臂动力学的主要方法有牛顿-欧拉法、拉格朗日法、高斯法、凯恩法、计算力矩法。其中，牛顿-欧拉法是对机械臂的每个关节构建牛顿方程和欧拉方程的方法，推导过程简便、利于编程且计算速度较快，适合各种动力学计算。但由于NAO机器人具有三维、多自由度机构，所以利用牛顿力学建模非常困难。综合对比其他方法，本文选择只需要速度而不必求内作用力的拉格朗日法。

机械运动系统的拉格朗日函数在广义坐标系中为

L=T-V

(6)

其中：L为拉格朗日量；T为系统动能；V为系统势能，则系统动力学方程为

(7)

其中i=1，2，…，n；ξi为与广义坐标qi相关的广义力。

在广义坐标下，τ为作用在机器人手臂上的力，则系统动力学方程变换为

(8)

NAO机器人左臂参数见表2。

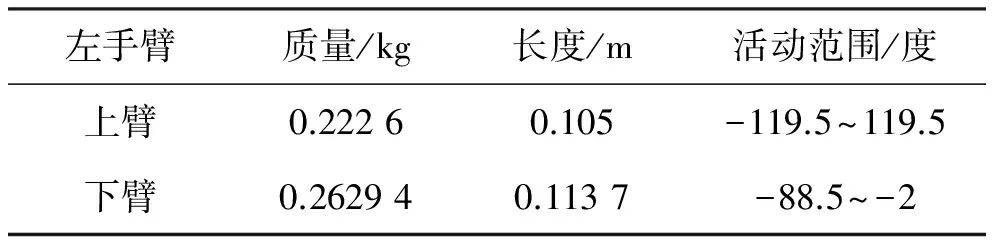
表2 左臂参数

以基座坐标系为参照，NAO机器人手臂的总动能为

(9)

总势能为

V=V1+V2=-(m1l1+m2l1)gcθ1+m2gl2c(θ1+θ2)

(10)

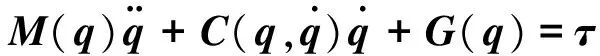
(11)

其中

M(q)=

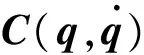
2 NAO机器人手臂PD控制及其仿真

当机器人手臂的结构及参数确定时，可以通过运动学及动力学模型描述系统完整的动态特性，从而应用各种控制方法，设计基于模型的控制器，实现机器人的轨迹跟踪控制，使得机器人的位置、速度以及加速度等变量具有理想的跟踪状态。常用的控制方法有PID控制、自适应控制、鲁棒控制、神经网络控制和模糊控制等[8-9]。

2.1 NAO机器人手臂PD控制器设计

PD控制器无论是在生产过程中还是在实际控制系统中已经得到大规模的应用了，与其他各类控制器相比，其优点是操作简单，运用方便。

忽略重力和外加干扰，采用独立的PD控制策略，NAO机器人的动力学模型为

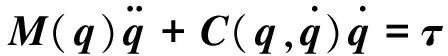
(12)

独立的PD控制律为

(13)

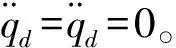
此时，机器人手臂动力学方程为

(14)

2.2 NAO机器人手臂PD控制仿真结果分析

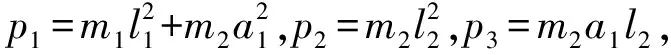
(15)

(16)

Simulink仿真图如图4所示。

图4 PD控制机械臂Simulink仿真

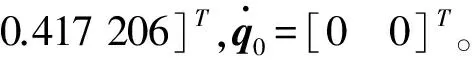
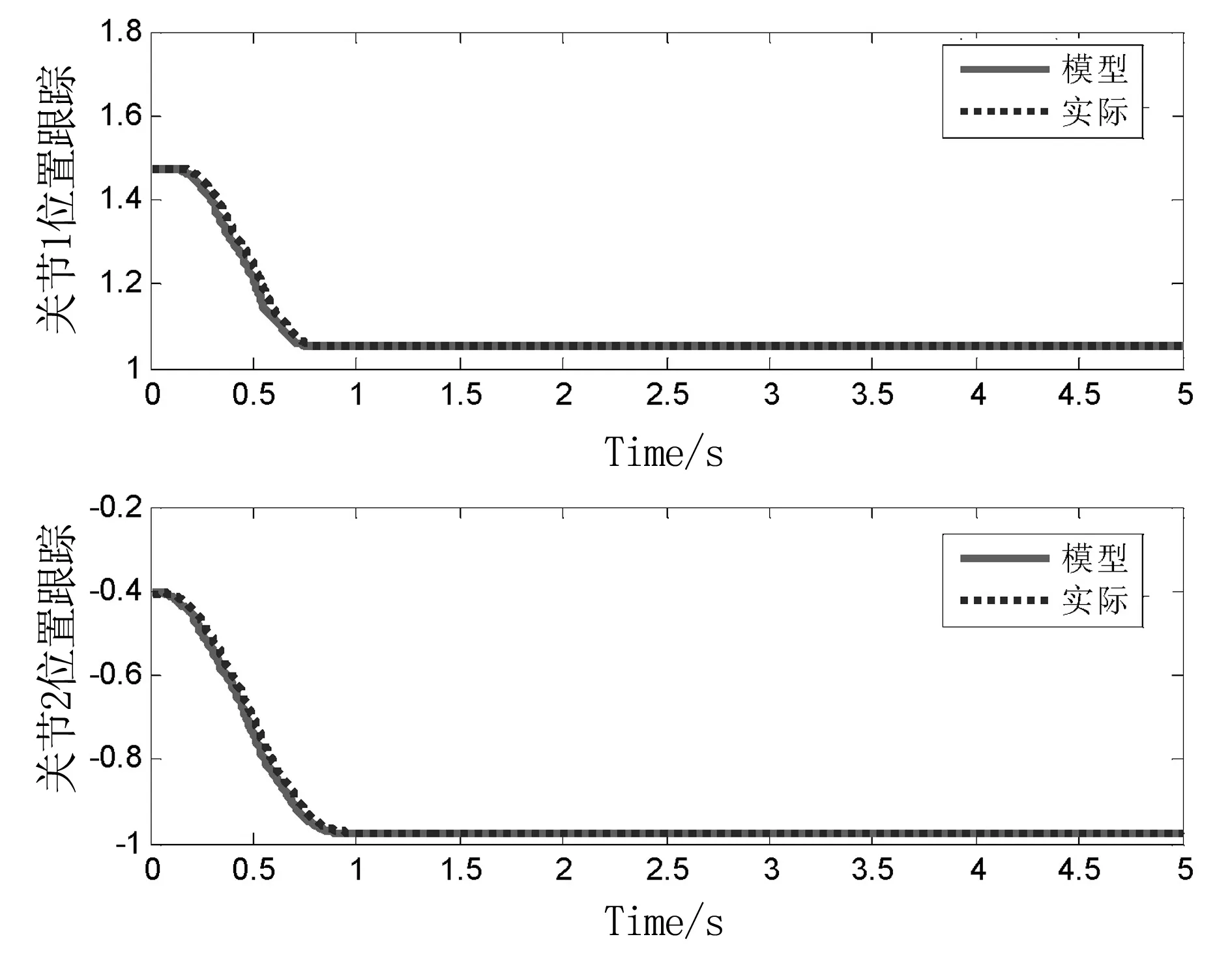
图5 PD控制关节位置

图6 PD控制的NAO手臂关节的控制力矩

由图5和图6可知，独立PD控制在没有扰动和干扰的情况下具有较好的跟踪输入能力，曲线看起来比较光滑，误差较小。独立的PD控制对机械臂运动控制的分析有着重要意义，它是后续优化控制策略设计的基础。

完全不受外力没有任何干扰的机械臂系统是不存在的，因而加入一个如图7所示的阶跃扰动信号进行仿真实验，仿真结果如图8所示，由图8可知其位置跟踪效果明显是不理想的。

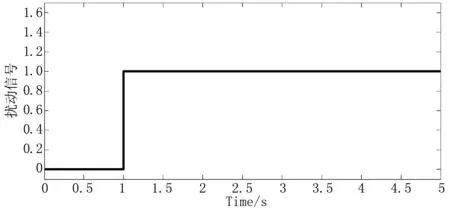
图7 扰动信号图

图8 加入扰动后的位置跟踪

3 NAO机器人手臂鲁棒自适应PD控制及其仿真

3.1 NAO机器人手臂鲁棒自适应PD控制器设计

本文NAO机器人手臂控制系统的动力学模型是非线性的，而独立的PD控制忽略了系统中非线性因素的影响。鲁棒自适应PD控制器结合了非线性PD控制和自适应反馈控制，可使控制系统获得较好的性能。

NAO机器人手臂动态性能的二阶非线性微分方程为

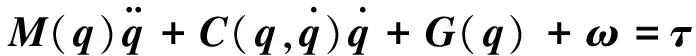
(17)

针对NAO机器人手臂系统，本文设计的控制器所需的动力学特性如下：

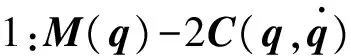
特性2：惯性矩阵M(q)是对称正定矩阵，存在正数m1，m2满足如下不等式：

m1‖x‖2≤xTM(q)x≤m2‖x‖2

(18)

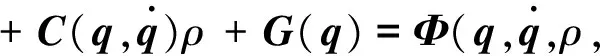
(19)

此外还需做出如下假设：

假设1：qd∈Rn为期望的关节角位移，qd的一阶导数和二阶导数存在。

假设2：误差和扰动ω的范数满足：

(20)

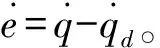
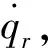
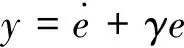
(21)

(22)

其中常数γ>0，则

(23)

(24)

在误差扰动信号的上确界已知的情况下，保证系统全局稳定的控制器的自适应律为

(25)

其中

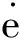
(26)

3.2 NAO机器人手臂鲁棒自适应PD控制仿真结果分析

图9 自适应PD控制Simulink仿真

令误差扰动为

(27)

初始状态为

(28)

式(25)中控制器参数取

αi=βi=1(i=1,2)，γ=5，仿真结果如图10所示。

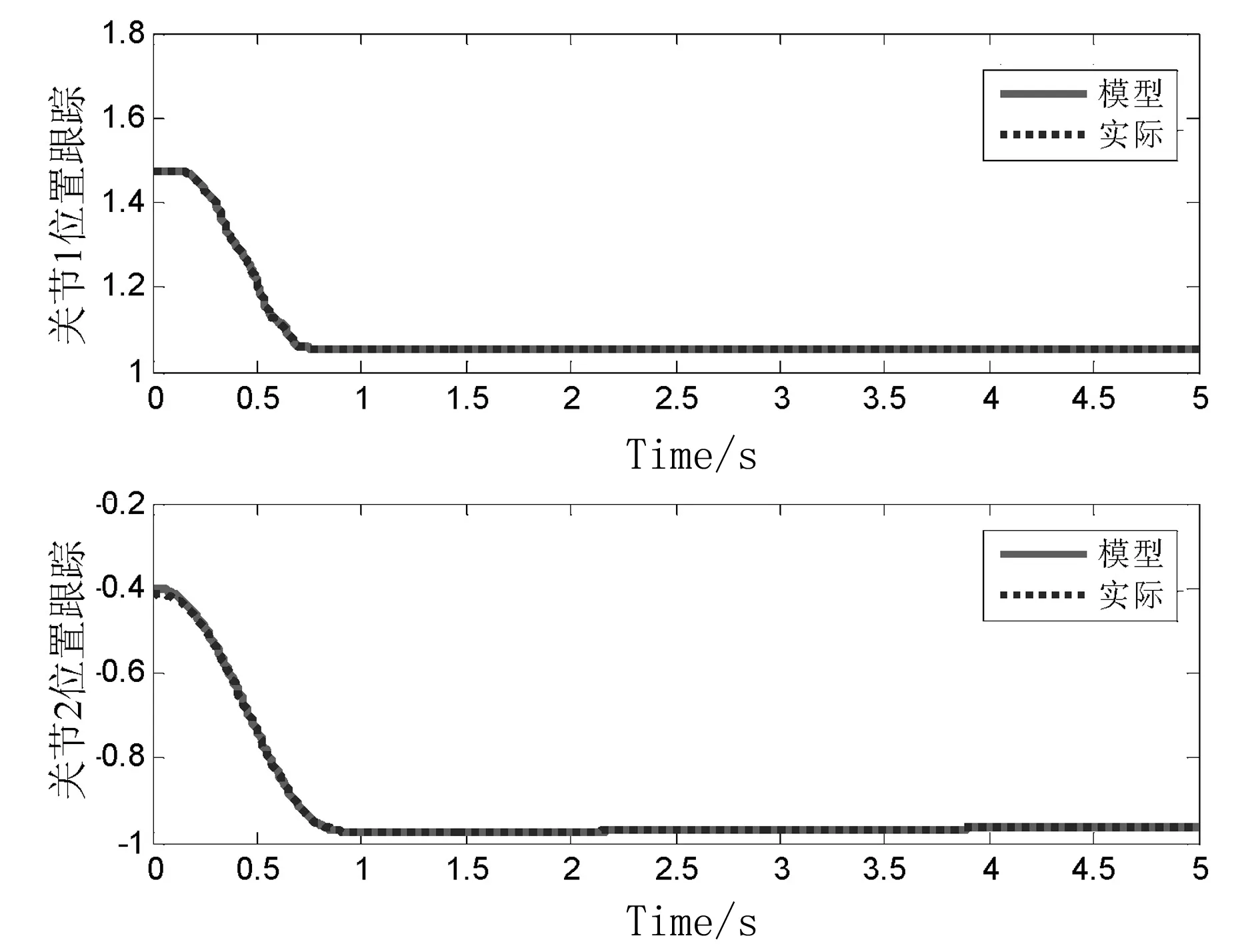
图10 自适应PD控制关节位置

加入与2.2相同的扰动后，仿真结果如图11所示。

图11 加入扰动后的位置跟踪

从仿真结果可以看出，当系统存在较大扰动时，自适应PD控制器对机器人手臂运动具有很好的跟踪性和鲁棒性。

4 结 论

利用D-H方法构建了NAO机器人的运动学

模型。在运动学分析基础上得出NAO机器人手臂的动力学模型，进而以此模型为依据设计PD控制器。针对PD控制结果在扰动时存在位置跟踪不理想状况，提出自适应控制来改进对NAO机器人手臂的运动跟踪控制。从仿真结果可以看出，自适应PD控制减小了稳态误差，即PD控制器对机械臂末端具有较好的轨迹跟踪控制效果。

[1] Kofinas N, Orfanoudakis E, Lagoudakis M G. Complete analytical forward and inverse kinematics for the NAO humanoid robot[J]. Journal of Intelligent & Robotic Systems, 2015, 77(2):251-264.

[2] 姜静,曹松,李宏达. 重力补偿的机械臂轨迹跟踪研究[J]. 沈阳理工大学学报,2016,35(2):5-9.

[3] 金国光,尉静娴,刘艳茹,等. 刚-柔耦合机械臂动力学建模及其振动抑制研究[J]. 天津工业大学学报,2014,33(06):65-69.

[4] Kelly R. Global positioning of robot manipulators via PD control plus a class of nonlinear integral actions[J]. IEEE Transactions on Automatic Control, 1998, 43(7):934-938.

[5] 布鲁诺·西西里安诺. 机器人学 : 建模、规划与控制[M]. 西安：西安交通大学出版社, 2015.

[6] 柏滢. GAMMA300型七自由度机械臂建模与仿真[D]. 太原：中北大学, 2015.

[7] 王智兴, 樊文欣, 张保成,等. 基于Matlab的工业机器人运动学分析与仿真[J]. 机电工程, 2012, 29(1):33-37.

[8] 霍伟. 机器人动力学与控制[M]. 北京：高等教育出版社, 2005.

[9] 刘金锟. 机器人控制系统的设计与MATLAB仿真[M]. 北京：清华大学出版社, 2008.