基于几何中心与卡尔曼滤波的路径跟踪算法

陈 鹏， 刘卫光， 王 璐

(中原工学院 计算机学院， 河南 郑州 450007)

割草机器人为完成任务需要遍历割草区域，波纹覆盖是一种常用且有效的遍历方式。它是一种由区域的外围螺旋推进至区域中心的遍历方式。在割草机器人的割草过程中，已割区域和未割区域之间会存在草地边缘，通过跟踪这样的草地边缘，可以实现波纹覆盖，从而将覆盖问题转化为路径跟踪问题。

草地边缘路径的跟踪属于一种特殊的目标跟踪。传统的目标跟踪方法，比如帧间差分法，是将前后两帧图像对应像素相减来检测目标[1-3]。此类方法需要被跟踪目标的每一个特征值在每一帧图像中都大致相同，而在路径跟踪当中，由于路径形状在不断地变化，只有少量的特征值是相同的，所以此类方法并不适用于路径跟踪。还有一类以控制为主的方法，比如PID算法，它是在机器人运动过程中，按偏差的比例(P)、积分(I)和微分(D)对机器人进行控制。此类方法虽然运算速度快，但是控制量会在理想值附近徘徊。为了使控制量趋于理想值需要一些时间，有一定的滞后性。还有一类方法是状态估计跟踪方法[4]，最典型的就是模型预测控制算法，它对运动学模型进行了线性化[5]。此方法通过模型预测得到控制量，虽然解决了滞后性的问题，但需要建立适合的模型并且数学运算复杂，算法运算速度慢。

另外，由于机器人处于室外环境，受风力、地形等因素的影响，系统容易受到各种随机干扰，进行草地边缘路径跟踪时需要考虑不稳定的误差带来的影响。

基于以上问题，针对割草机器人提出了基于几何中心与卡尔曼滤波的路径跟踪算法，以跟踪割草边缘并提高控制精度。

1 基于几何中心的路径跟踪算法

本文算法使用机器人视觉来进行路径跟踪。首先利用机器人摄像头获取当前时刻的图像；然后对此图像进行草地边缘的检测，得到一张边缘清晰的二值图像；接下来取草地边缘与图像上下边界的交点构成直线，作为机器人行走路径，也可以利用最小二乘法进行直线的拟合[6]。路径拟合图如图1所示，方块代表摄像头获取的每一帧图像，虚曲线AE是实际草地边缘，机器人的实际行走路径为黑色线段。

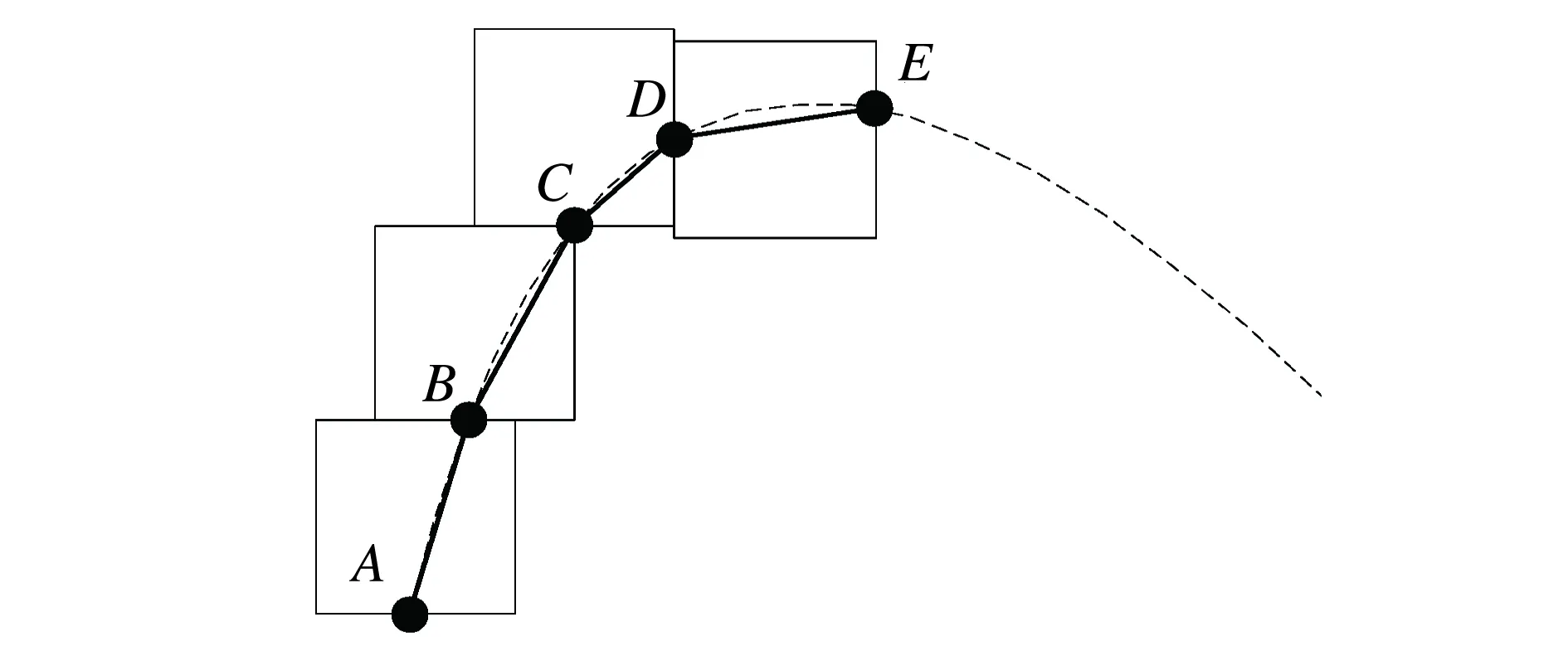
图1 路径拟合图

由于摄像头固定安装在机器人前后中轴线的正上方，所以拍摄图像的中心线与机器人运动方向重合。算法的重点就是分析当前图像帧，计算所拍摄图像的中心线与直线路径(根据草地边缘拟合而成)的几何位置关系，控制机器人偏转适当角度及位移适当距离，从而使直线路径与所拍摄图像的中心线尽量重合，即控制机器人沿直线路径运动(路径跟踪)。具体步骤如下：

(1)以正方形图像的中心为原点建立笛卡尔直角坐标系(如图2所示)，取草地边缘与图像边界相交的两点来构造直线方程。

(2)和上一帧图像的中心线(假定已与机器人行走路径重合)进行分析与计算，得到偏转角度。

(3)基于偏转角度，旋转当前帧的图像，使前后两帧图像中的直线平行，这两条直线中心的距离即为偏移距离。

如图2所示：(a)表示当前帧的图像，其中虚线l1为上一帧的中心线，l2为当前帧的草地边缘拟合直线，l1与l2之间的夹角为θ；(b)表示旋转θ度之后的图像，偏移距离为h。

图2 旋转前后的图像

1.1 偏转角度的确定

(1)

(2)

于是可求得l1与l2的夹角θ1。

(3)

同理可以求出tn时刻的偏转角θn。

(4)

(5)

(6)

1.2 偏移距离的确定

(7)

于是可求出偏移距离h为：

(8)

2 基于卡尔曼滤波器的误差控制

由于机器人处于室外环境，容易受到各种随机干扰。为了缩小随机干扰造成的误差，可以利用卡尔曼滤波来提高跟踪精度[7]。

卡尔曼滤波器是一种递推形式的状态和参数估计方程，通过状态方程进行预测，通过观测误差来进行校正，从而不断降低误差[8]。一般卡尔曼滤波分为状态预测过程和更新过程两个部分[9]。

根据基于几何中心的路径跟踪算法，把需要跟踪的直线转化为这条直线的中心点，这样将跟踪目标由线转化为点。虽然实际情况中机器人是在运动的，但是根据坐标系的相对性，观测点也可以看作是在不断地运动。假设在一系列的图像中，以图像中心为原点建立坐标系，t时刻跟踪目标点的坐标为(xt，yt)，经过卡尔曼滤波预测后，t+1时刻的预测坐标为(xt+1，yt+1)，协方差为∑(xt,yt)。

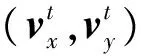
Xt+1=At+1,t·Xt+Wt

(9)

式中：At+1,t为状态转移矩阵;Wt为均值是0、协方差是Q的白噪声。

由于假设直线中点的运动为匀速运动，并且两帧图像之间的位移很小，以Δt表示相邻帧的时间间隔，则状态转移矩阵为：

(10)

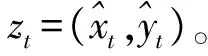
Zt=Ht·Xt+Vt

(11)

其中，Vt为均值是0、协方差是R的白噪声。

由于观测值只与位置有关，所以设定观测矩阵为：

(12)

由此，得到系统的状态方程和观测方程为：

(13)

(14)

式中，Wt与Vt在实验过程中随机设定。

由式(9)-(12)可以得到卡尔曼滤波的预测方程以及更新方程。

预测方程为：

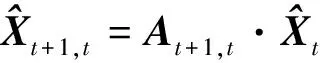
(15)

(均方误差预测)

(16)

更新方程为：

(卡尔曼滤波增益)

(17)

(滤波估计方程)

(18)

Pt+1=(I-Kt+1·Ht)·Pt+1,t

(滤波均方误差更新矩阵,I是单位矩阵)

(19)

根据基于几何中心的路径跟踪算法，计算出偏移距离，据此再获得观测值。利用卡尔曼滤波预测出系统下一时刻的状态，并根据观测值不断地更新系统的状态以及误差方程，达到控制误差的目的，使得机器人的路径跟踪更加精准。

3 实验结果分析

应用本文所提出的基于几何中心和卡尔曼滤波的路径跟踪算法，对路径跟踪过程进行仿真实验验证。实验环境如下：PC配置为Intel Core 2.4 GHz,4 G内存，500 G硬盘；开发工具Visual Studio 2012；视频图像的分辨率为320×240，帧率为30帧/s。

图3所示为视频中连续的经过边缘检测后的二值图像。图3中：(a)为起始帧，相邻帧为(b)，依次直到最后一帧(h)。两帧之间的时间间隔为0.5 s。计算出当前帧图像中路径与前一帧图像中路径的偏转角度以及偏移距离，见表1。表中的偏移角度采用正切值形式表示，偏移距离的单位为像素，即像素的个数。

图3 连续的二值图表1 计算结果

相邻两帧偏移角度正切值偏移距离/像素(a)，(b)0．07251(b)，(c)0．15229(c)，(d)0．62217(d)，(e)0．1595(e)，(f)0．0551(f)，(g)0．0835(g)，(h)0．0630

图4与图5显示了加入卡尔曼滤波之后的跟踪过程中偏移距离以及偏移角度的变化。可以看出，偏移距离在不断地减少；经过不断的调整，误差在不断缩小，并且在时间性能上，经过7帧的迭代便可以有效地跟踪到路径。

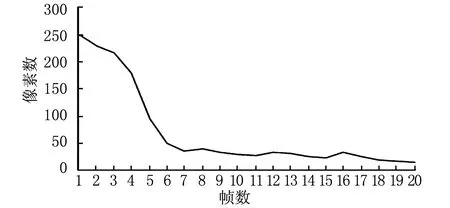
图4 偏移距离变化图

图5 偏移角度变化图

为了测试本文算法的实时性，采用当前比较流行的传统路径跟踪算法进行对比实验[10]，它们的运行时间如表2所示。从表2可看出，相对于其他传统算法，本文算法的运行时间明显较少，可以对路径实现实时跟踪。

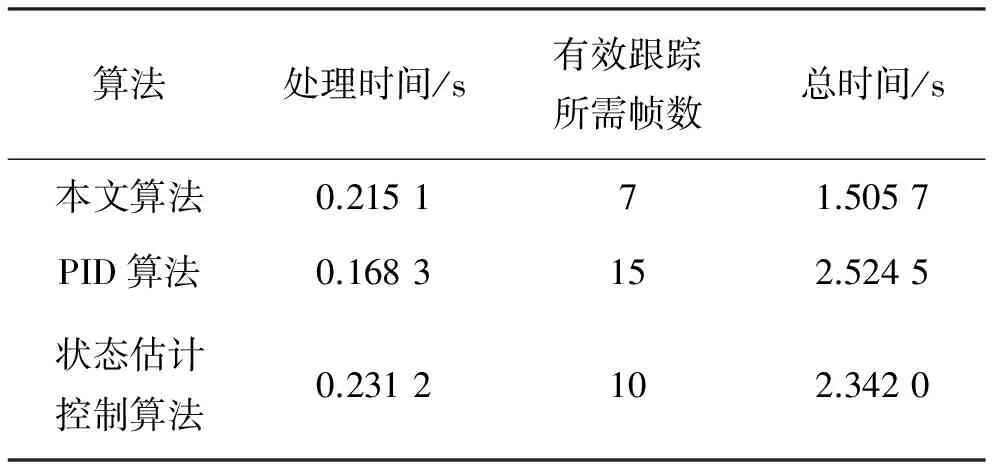
表2 不同算法运行时间

4 结 论

本文针对割草机器人路径跟踪的问题，提出了基于几何中心与卡尔曼滤波的路径跟踪算法。此算法可以实时获取路径偏移情况，并且可以使图像中心持续保持在路径之上，避免产生偏离状况，在融入卡尔曼滤波器之后使得控制更加精准。

[1] 张鑫.基于机器视觉的目标检测定位与路径控制方法研究[D].北京：北京交通大学, 2015.

[2] 高飞，蒋建国，安红新，等.一种快速运动目标检测算法[J].合肥：合肥工业大学学报(自然科学版), 2012，35(2):180-183.

[3] 沈瑜，王新新.基于背景减法和帧间差分法的视频运动目标检测方法[J].自动化与仪器仪表，2017(4):122-124.

[4] 张文俊.机器视觉目标跟踪算法研究[D].太原：太原科技大学，2014.

[5] 余永超，赵明国. 自主驾驶自行车的改进路径跟踪算法[J]. 华中科技大学学报(自然科学版), 2015(S1):345-350.

[6] 刘波，耿韬.基于改进最小二乘法拟合的车道线检测[J]. 信息技术，2015(4):192-195.

[7] 陈玥.移动机器人视觉定位系统的研究与设计[D]. 长沙：中南大学，2005.

[8] 张博峰.基于机器视觉的自主无人车道路识别研究[D]. 西安：西安工业大学，2014.

[9] 杨平，厉小润.基于二级特征匹配的卡尔曼滤波跟踪算法[J].有色冶金设计与研究，2011，32：34-37.

[10] 李林琛，蒋小平.基于PID控制的移动机器人路径跟踪[J].激光杂志，2016(2):110-112.