基于ABAQUS的钢管混凝土框架结构动力特性研究

赵 毅, 李 飞, 翟帅帅

(中原工学院 建筑工程学院， 河南 郑州 450007)

钢管混凝土框架结构在高层建筑工程领域中的应用越来越广泛[1-3]，而框架结构的动力特性分析是钢管混凝土框架结构分析研究的热点之一。地震强度的不确定性直接导致钢管混凝土框架结构在未来可能进入弹塑性变形阶段的不确定性。框架结构在线性阶段和弹塑性阶段的反应不同，这不仅表现为框架结构的基本动力特性在非线性反应阶段时时刻刻都发生着变化，而且还表现为框架结构在线性阶段与非线性阶段的动力特征截然不同[4-6]。本文采用ABAQUS有限元分析软件对钢管混凝土柱-钢梁框架结构进行数值模拟，探讨其振型与模态，并分析框架结构的动力特性，为该类结构的地震相应研究提供一定指导。

1 有限元模型的选取

采用ABAQUS有限元软件，选取钢管混凝土框架结构在地震作用下的实验[7]作为研究对象，缩尺模型构件总设计8层，每层高度350 mm，两开间及进深均为600 mm，钢管直径为68 mm，内部填充C30碎石混凝土，楼板内配置直径为2.2 mm的镀锌铁丝，并用20 mm厚的C20混凝土浇筑，钢管与H40*45*2.5*3的钢梁焊接，模型总质量为760.00 kg。钢管混凝土柱-钢梁框架的材料强度和屈服抗压强度平均值见表1，其结构构件尺寸如图1所示。

2 单元类型的选取

理论上，ABAQUS的所有单元均可用于动态分析，选取单元的一般原则与静力分析相同。为了满足计算时间耗损及精度的要求，钢管混凝土和钢梁均采用Beam单元，由于各层楼板均配置有直径为2.2 mm的镀锌铁丝网，因此楼板均采用分层壳体单元。

表1 材料强度及屈服抗压强度平均值 MPa

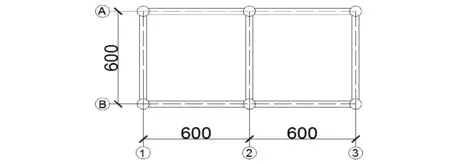
(a) 框架结构平面图

(b) 框架结构立面与侧面图图1 框架结构模型尺寸示意图

基于钢管混凝土统一强度理论建立钢管混凝土框架结构的有限元模型，并对框架结构的模态进行分析。网格的划分如图2所示。

(a) 钢框架 (b) 三维框架 (c) 楼板图2 框架结构网格划分示意图

3 有限元全过程分析

3.1 自振频率分析

ABAQUS/Standard提供了两种特征值提取方法：Lanczos方法和子空间迭代法(subspace iteration)。当模型的规模较大，且需要提取多阶振型时，Lanczos方法的速度更快，精度更高。

经综合分析，本文采用Lanczos方法。虽然框架模型的几何形状具有对称性，但不能只对1/2或1/4的模型进行建模，因为这样无法描述反对称振型，因此，本文对整个框架结构进行建模。经计算得到的特征值输出见表2。表2中广义质量表示为对应于相应振型的单自由度系统的质量。

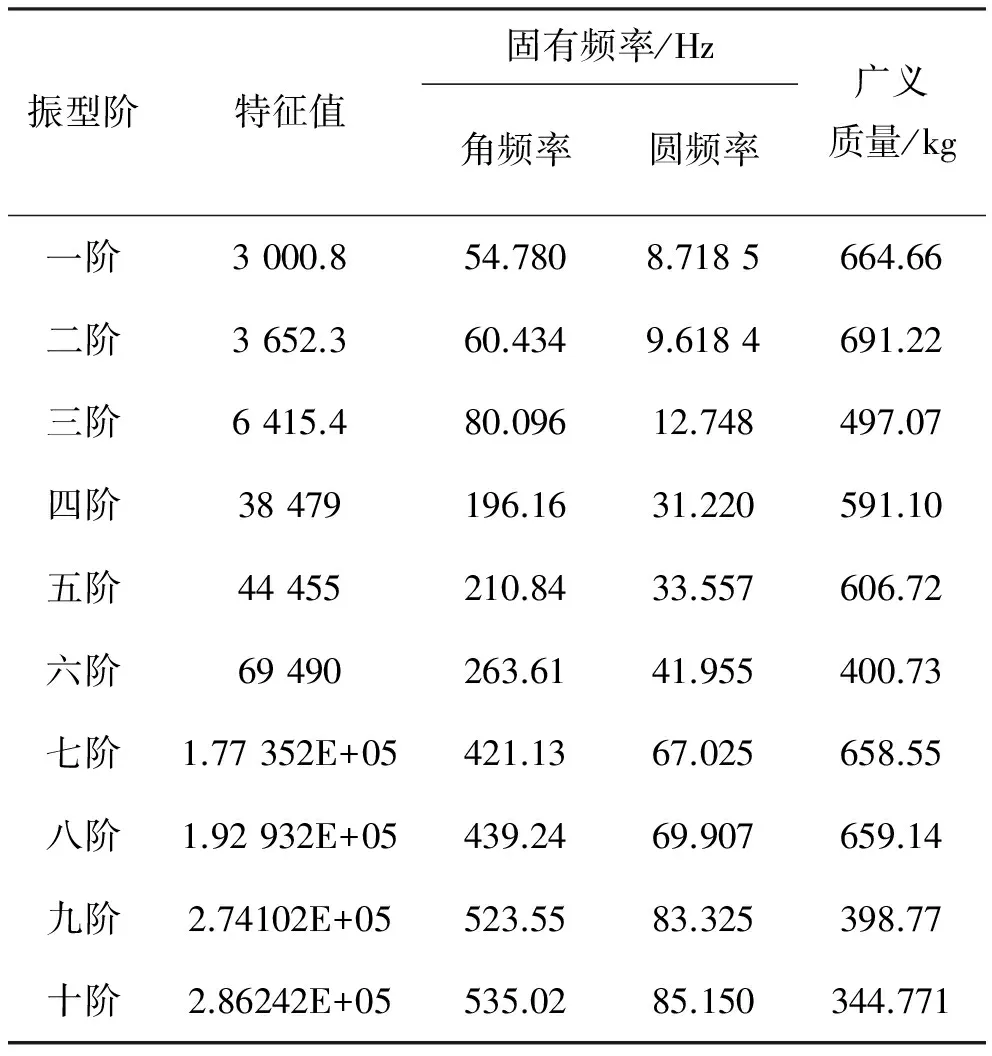
表2 特征值输出

从表2可以看出，前十阶振型中所提取的圆频率最高频率为85.150 Hz。

对钢管混凝土柱-钢梁框架结构进行计算，得到参与系数与有效质量分别见表3和表4。

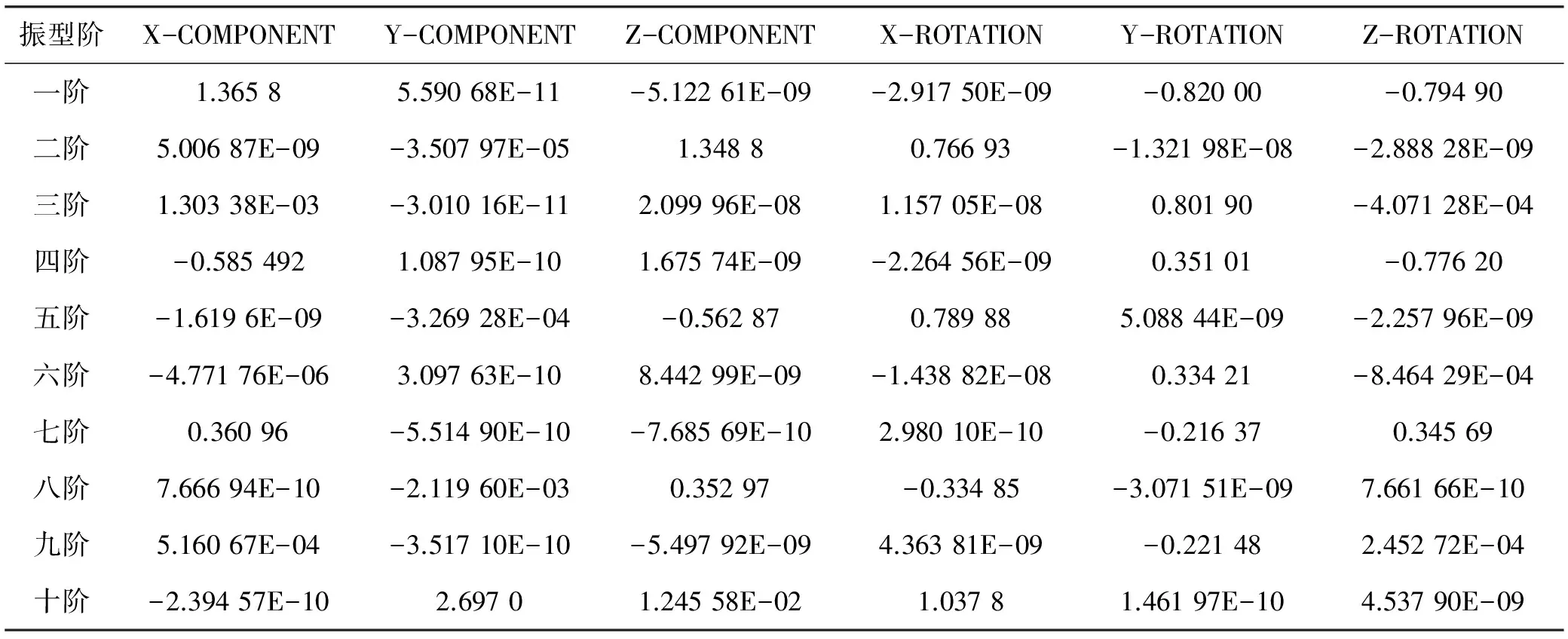
表3 参与系数

表3反映了振型在各自由度上起主导作用。由表3可知，第一、三、四、六、七、九阶振型主要在X方向上发生平动，第二、五、八阶振型主要在Z方向上发生平动，而第十阶振型主要在Y方向上发生平动。第二、五、八、十阶振型在X方向上发生转动，第一、三、六、九阶振型主要在Y方向上发生转动，第四、七阶振型主要在Z方向上发生转动。

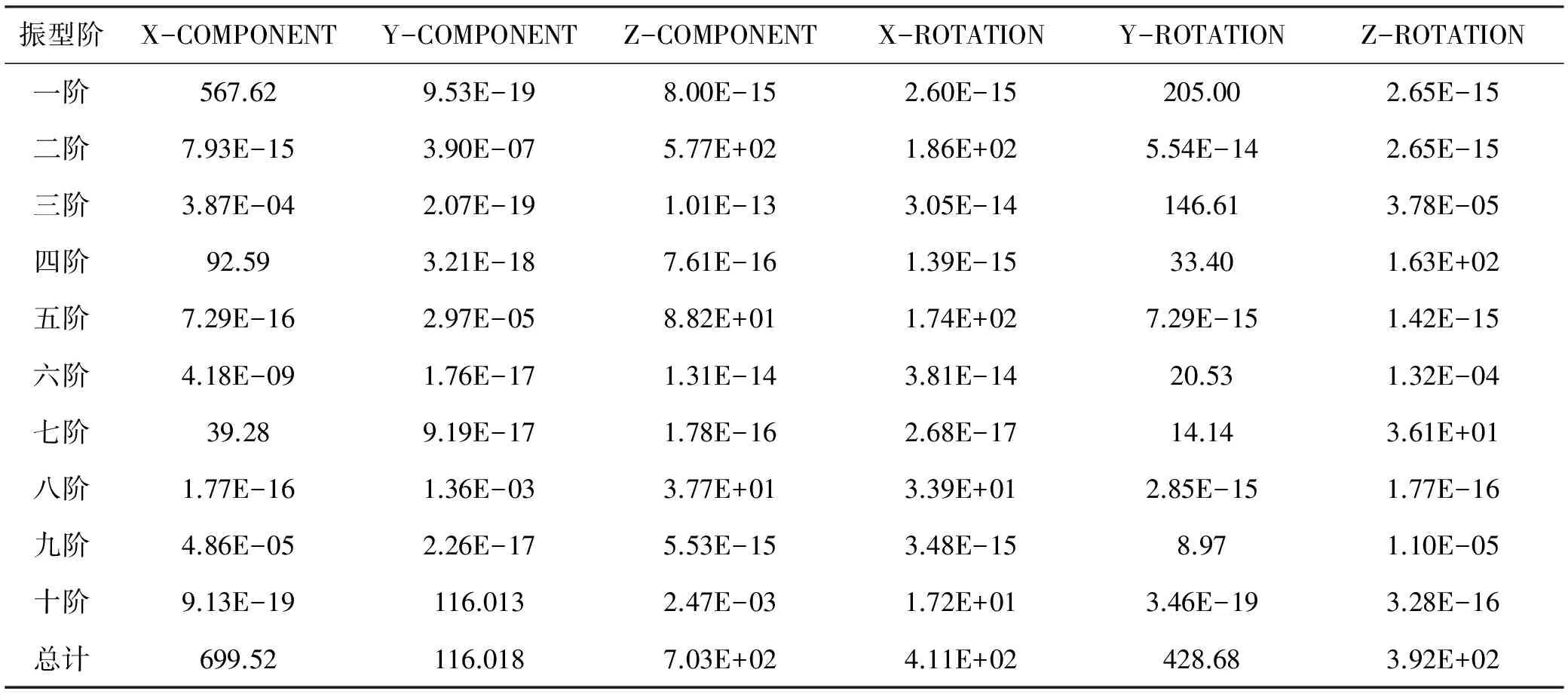
表4 有效质量 kg

表4反映了框架结构的各阶振型在各个自由度上所激活的质量。由表4可知，在X方向上具有显著质量的最低阶振型是第一阶，在Y方向上具有显著质量的最低阶振型是第十阶，在Z方向上具有显著质量的最低阶振型是第二阶。模型的总质量为760.00 kg。

在使用振型叠加法分析线性动态问题时，要保证在频率提取分析中提取足够数量的模态，其判断标准是在主要运动方向上的总有效质量要超过模型中可运动质量的90%。本文钢管混凝土柱-钢梁框架主要在Z方向发生运动。从表4中数据可以看出，在Z方向上总的有效质量为703.02 kg，模型的总质量为760.00 kg。由于受约束的节点占全部节点的比例很小，可以近似地认为模型中可运动的质量等于模型的总质量。这样在Z方向上总有效质量占模型总质量的比例是703.02/760.00=92.5%，因此提取前十阶振型是足够的。

3.2 模态分析

上述过程已经完成了对框架结构自振频率的提取分析，相应的自振周期为1/85.150=0.011 7 s。模态动态分析步中的时间增量小于此周期值，因此，在模型的基础上添加一个模态分析步。

图3所示为前五阶振型框架结构的网格划分示意图，其模拟计算结果与实验结果对比见表5。

(a)一阶模态 (b)二阶模态 (c)三阶模态 (d)四阶模态 (e)五阶模态图3 框架结构网格划分示意图表5 仿真模拟与实验数据对比表

一阶二阶三阶四阶五阶仿真数据8．729．6212．7531．2233．56实验数据9．6110．9418．3431．8835．53

由图3可知，第一阶振型和第二阶振型主要是在X、Z方向上发生平动，而到框架结构的第三阶振型时，模型不仅在X方向上发生了平动，还发生了Y方向的扭转，第四、第五阶振型分别在Z、X方向上发生了扭转效应。这是因为在模拟分析中，质量在整个框架结构中的分布是相对均匀的，而且平面分布较为规则，所以前两阶振型都没发生扭转，表明框架结构模型的刚度较好且分布均匀。

从表5可以看出，由第一阶至第五阶振型仿真模拟得到的自振频率均比实验所得的自振频率小，但是从各阶数据来看，仿真数据与实验数据在对应阶段数据增量情况极相似，说明这两个过程的增长趋势相同。造成仿真模拟数据偏小的主要原因是，与实验相比，仿真模拟的环境是理想的，而实验过程要受到周围环境、实验器材、实验条件以及人为因素的影响，这必然会对实验结果造成一定的影响，所以仿真模拟数据的整体性偏小也在情理之中。

4 结 语

(1)楼板采用分层壳体单元简化了计算模型，缩短了计算时间，模拟结果良好。

(2)框架结构的前两阶振型并未发生扭转效应，整个结构刚度较好且分布均匀。

(3)数值模拟与实验结果吻合较好，验证了有限元模型的正确性。

[1] 付博啸. 多层钢管混凝框架结构抗震性能研究[D]. 兰州：兰州理工大学, 2012.

[2] 尧国皇, 王卫华, 郭明. 超高层钢框架-钢筋混凝土核心筒结构弹塑性时程分析[J].振动与冲击，2012,31(14):137-151.

[3] 王先铁, 郝际平, 周观根, 等. 两层两跨方钢管混凝土框架抗震性能试验研究[J]. 地震工程与工程振动, 2010, 30(3):70-76.

[4] 黄襄云,周福霖. 钢管混凝土结构地震模拟试验研究[J]. 西北建筑工程学院学报(自然科学版),2000, 17(3):14-17.

[5] 张园,毕刚,李斌. 钢管混凝土框架结构抗震性能试验研究[J]. 地震工程与工程振动,2002,22 (5):53-56.

[6] 王文达,韩林海,陶忠. 钢管混凝土柱-钢梁平面框架结构抗震性能的试验研究[J].建筑结构学报,2006,27(3):48-58.

[7] 杜国峰,徐礼华.钢管混凝土框架结构抗震性能[J]. 哈尔滨工业大学学报,2009，41(10):123-128.