面向车辆操纵稳定性的主动差速器模型预测控制∗

冀 杰，黄岩军，李云伍，张 春，高书娜

前言

随着人们对汽车主动安全性能要求的不断提高，如何有效改善车辆在恶劣行驶工况下的操纵稳定性已经成为车辆动力学控制的重要研究领域。目前，对车辆左右两侧车轮施加不同的制动力并产生必要的校正横摆力矩，是有效提升车辆操纵稳定性的重要手段，例如电子稳定程序(ESP)、车辆稳定控制系统(VSC)等。然而，此方法在提高车辆操纵稳定性的同时，会损失一定的汽车动力性能，难以满足赛车或高性能运动型轿车对动力性能和驾乘乐趣的要求[1]。

近年来，汽车主动差速器概念的提出与研究为改善车辆操纵稳定性提供了一条新的思路。主动差速器能够根据车辆的行驶工况和路面状态，将驱动力矩主动分配给驱动轴两侧的驱动轮，从而产生主动横摆力矩并使车辆跟踪期望的横摆角速度和车身侧偏角[2]。该机构的工作原理与差速制动相似，都是充分利用了轮胎纵向力线性范围大于侧向力线性范围的特性，而差速驱动的方法能够在产生主动横摆力矩的同时，解决传统差速制动方法造成的动力性能损失过大的问题[3]。目前，国内外学者对主动差速器的动力学特性和驱动力矩分配控制进行了大量前期研究。例如，文献[4]中首先提出了主动差速器的基本结构并对其动力传递过程和控制进行了介绍和分析。文献[5]中建立了主动差速器的动力学以及运动学模型，并分析了传动轴以及轮胎非线性力对主动横摆力矩产生的影响。文献[6]中应用二阶滑模控制算法对车辆的横摆角速度进行控制，并考虑了车辆运动工况的不确定性和控制变量的饱和特性，从而有效跟踪车辆的期望横摆角速度。然而，上述操纵稳定性控制方法主要以当前的横摆角速度跟踪误差作为控制依据，无法预测并利用车辆未来的运动状态信息，这与人类的实际驾驶操作行为存在较大的差异。近年来，模型预测控制逐渐成为车辆操纵稳定性和驱动力矩控制的重要研究方向之一，该方法能够利用车辆动力学预测模型获得未来有限时域内的车辆动力学状态参数，并通过求解有限时域内有约束条件的最优控制问题，获得主动差速器的驱动力矩分配比例并提高车辆的操纵稳定性[7]，例如，文献[8]和文献[9]中将模型预测控制方法应用到电动汽车轮毂电机的驱动力矩主动分配中，仿真结果证明了该方法在主动驱动力矩分配控制中的有效性，也为传统动力车辆的主动差速器模型预测控制提供了实践基础。

基于以上分析，本文中建立了基于主动差速器的车辆动力学预测模型，分析了影响车辆操纵稳定性控制的控制变量约束和输出变量约束，同时，将模型预测控制问题转换为标准的二次规划问题并利用内点法进行了求解。最后，在低附着系数路面上对基于主动差速器的整车操纵稳定性控制进行了仿真分析。仿真结果证明了提出的模型预测控制算法在操纵稳定性控制中的有效性，为赛车及高性能运动型轿车的综合运动控制提供一条新的途径。

1 车辆/主动差速器综合预测模型

1.1 双轴车辆线性动力学模型

假设(x，o，y)为固定于车辆质心处的车辆坐标系，所有角度均取逆时针方向为正且车辆在纵向运动方向的速度恒定为Vx，同时，忽略悬架系统及侧倾运动对车辆动力学特性的影响，并在动力传动系统中添加主动差速器动力学模型。建立如图1所示的双轴线性动力学模型示意图。

该模型直接以车辆的前轮转向角δ和驱动桥系统的输入轴转矩Ti作为系统输入，并假设前、后轴上左右两侧的轮胎横向力在车辆坐标系下对称相等，分别用Fyf和Fyr表示，而后轴左右两侧的轮胎纵向力分别用Fxl和Fxr表示。本研究将通过控制主动差速器左右两侧的驱动力矩分配比例，进而在后轴两侧产生不同的轮胎纵向力以及主动横摆力矩MY，达到提高车辆操纵稳定性的目的。前、后轴上轮胎横向力及主动横摆力矩可表示为

式中:Vy为车辆坐标系下的横向运动速度；ψ为车辆的横摆角度；Cyf和Cyr分别为前、后轴上两个车轮合并后的侧偏刚度系数；lf和lr分别为前轴和后轴到车辆质心的距离；lw为车辆后轴左右两侧车轮的轮距。

根据上述简化原则，利用牛顿第二定律对车辆动力学模型进行分析，得到以前轮转向角为输入变量、以后轴左右两侧轮胎纵向力为控制变量的状态空间模型为

状态变量Xv及各状态矩阵可表示为

式中:β为车辆的车身侧偏角；m为整车质量；Iz为整车绕z轴的转动惯量。

1.2 主动差速器动力学模型

根据Kaoru Sawas提出的主动差速器结构，忽略传动系统中各部件的弹性阻尼及其扭振、摆振等振动等因素，考虑输入轴、输出轴及驱动轮对主动差速器动力学的影响[10]，得出如图2所示的主动差速器结构示意图。

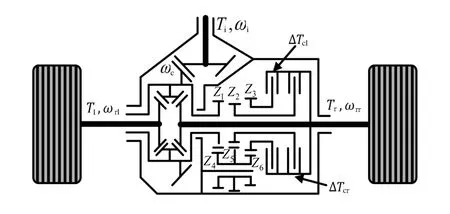
图2 主动差速器的结构示意图

对主动差速器中的齿轮组、主减速器齿轮、差速器行星齿轮以及制动器进行力矩平衡分析，并根据齿轮组中的齿轮齿数关系Z1＝Z2＝Z3＝42，Z4＝32，Z5＝36，Z6＝28，得到差速器输入转矩Td，驱动轴上左、右两侧制动器上的控制力矩ΔTcl和ΔTcr与两侧驱动力矩Tl和Tr之间的关系为

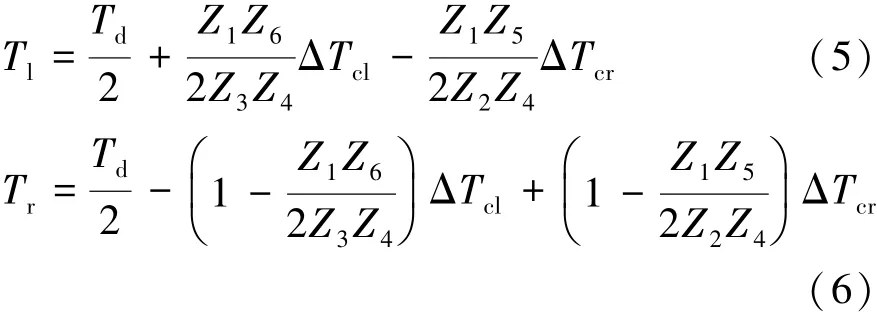
考虑主减速器的转动惯量Iin、主动差速器的转动惯量Id和主减速器的传动比Nf，得到驱动桥系统的输入轴转矩Ti与差速器输入转矩Td之间的动力学关系为

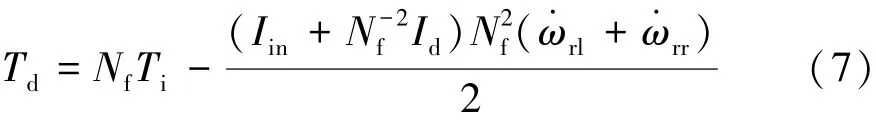
考虑左、右两侧轮胎的转动惯量Iwl和Iwr以及左、右两侧驱动轴的转动惯量Idl和Idr，并对主动差速器左、右两侧的驱动轴及车轮总成进行动力学分析，得

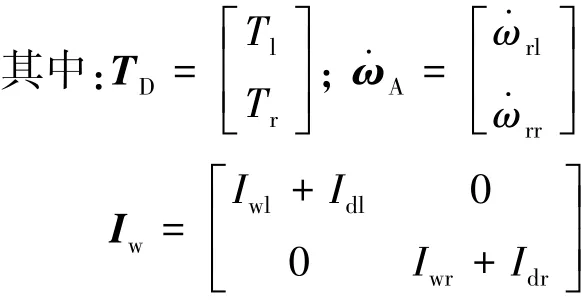
式中:Iw为车轮驱动轴总成的转动惯量矩阵；Rw为车轮有效转动半径。

当轮胎的纵向力处于小滑移率区域时，轮胎力Fxl和Fxr与纵向滑移率σxl和σxr可近似看作线性关系:

式中:Cx和σA分别为驱动轴左、右两侧轮胎的纵向刚度矩阵和滑移率矩阵。

而车轮滑移率与车轮转速之间的关系为

将式(7)、式(9)和式(10)代入到式(8)中，得到以后轴车轮纵向滑移率为状态变量的主动差速器状态空间模型为

其中:

1.3 车辆/主动差速器综合动力学预测模型

将轮胎纵向力计算公式(9)代入车辆动力学模型(4)中，并综合主动差速器的动力学模型公式(11)，得到车辆/主动差速器综合动力学状态空间模型为

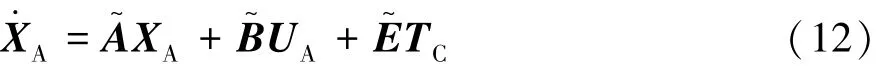
其中:

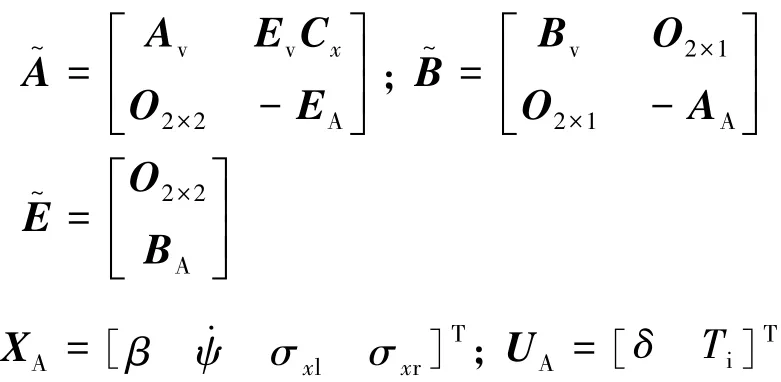
式中:XA为状态变量；UA为输入变量；TC为控制变量；Oi×j为具有 i行和 j列的零矩阵。

选择状态空间的输出变量为 YA＝Xv＝[β]T， 得到输出状态方程为

利用欧拉方法对车辆动力学模型公式(12)和式(13)进行离散化处理(ΔT＝0.01s是系统的采样时间)，得到线性定常离散时间的车辆动力学状态空间模型:

假设当前时刻k的所有状态向量XA(k)是可测量或可估计的，利用迭代模型公式(14)得到未来某时刻的状态变量XA(k+i)及输出变量YA(k+i)预测值。设定预测时域为Np＝6，控制时域为Nc＝6。另外，(k+i k )表示当前k时刻对未来k+i时刻的车辆动力学状态参数预测，最终得出车辆动力学输出变量的模型预测状态空间方程为

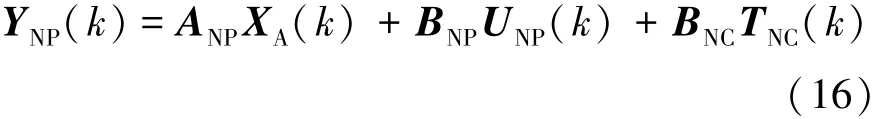
其中:

2 约束模型预测控制系统设计

车辆操纵稳定性模型预测控制的核心思想可描述为:在当前采样时刻k，根据测量或估计的车辆动力学状态变量XA(k)，获得未来预测时域Np范围内的输出状态信息YA(k+i k)，并基于期望信息在线求解约束最优化问题，最后将得到的控制变量作用于车辆动力学模型并不断重复上述过程[11]。

2.1 目标函数

将车辆的操纵稳定性控制问题转化为有限时域内的约束最优化问题[12]，定义能反映车辆操纵稳定性能指标的目标函数:

根据转弯半径R，前轮转向角δ和车辆动力学模型参数，得到车辆在稳态转向时的横摆角速度δ和车身侧偏角βδ参考值为

式中，L＝lf+lr，为车辆前、后车轴之间的轴距。

由于车辆的纵、横向轮胎力具有非线性饱和特性，根据车辆行驶速度变化以及道路参数，可设定横摆角速度ψ·max和车身侧偏角βmax的范围:

式中:μ为路面附着系数；g为重力加速度；Vr为车辆动力学的特征速度；参数k1和k2分别定为π/18和π/60[7]。

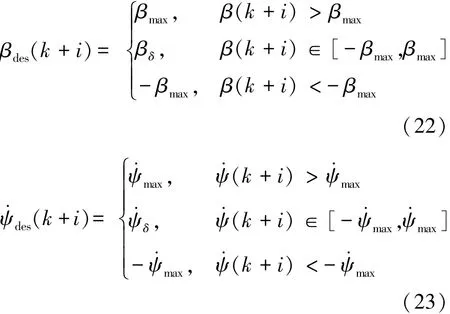
另外，根据差速器、传动齿轮和制动器的运动学关系可知，对主动差速器左侧和右侧的制动器同时进行控制将会造成运动干涉。因此，设定左、右制动器的控制力矩范围是ΔTc∈[-Tmax，Tmax]，当ΔTc>0时，表示右侧制动器工作；而ΔTc＝0时，表示左右两侧制动器同时松开；当ΔTc＜0时，表示左侧制动器工作，即:

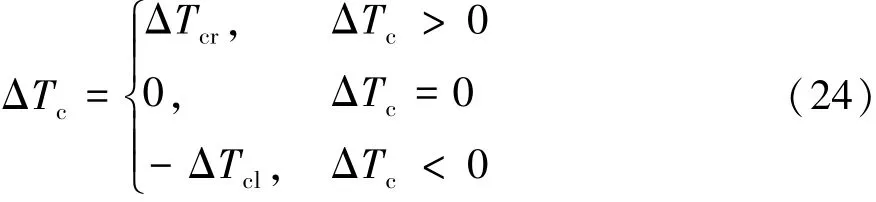
选择目标函数控制输入和跟踪误差的加权矩阵分别为R＝0.001·INc和Q＝I2Np，利用Um(k)表示控制时域Nc范围内的控制力矩输入向量:

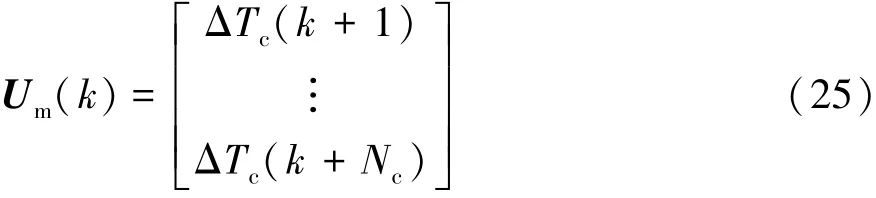
分别利用Rr(k)和Ym(k)表示预测时域Np范围内的车辆运动参考信息和实际输出状态信息:

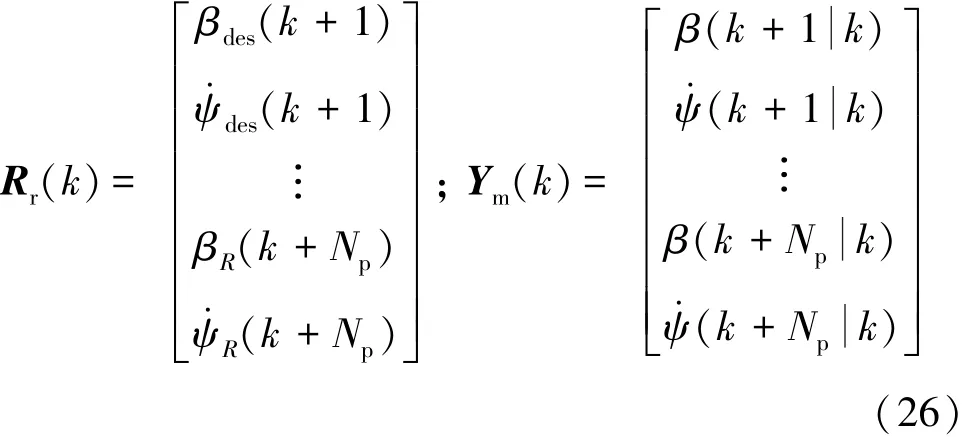
将式(25)和式(26)代入到目标函数式(17)中，得

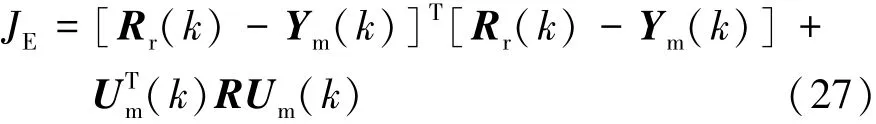
2.2 约束条件分析

由主动差速器的机械运动原理可知，根据驱动力矩的横向传递方向及右侧驱动轴与制动盘之间的速度差，能够判断对主动差速器的左侧还是右侧制动盘进行控制[13]，具体的控制规则如表1所示。

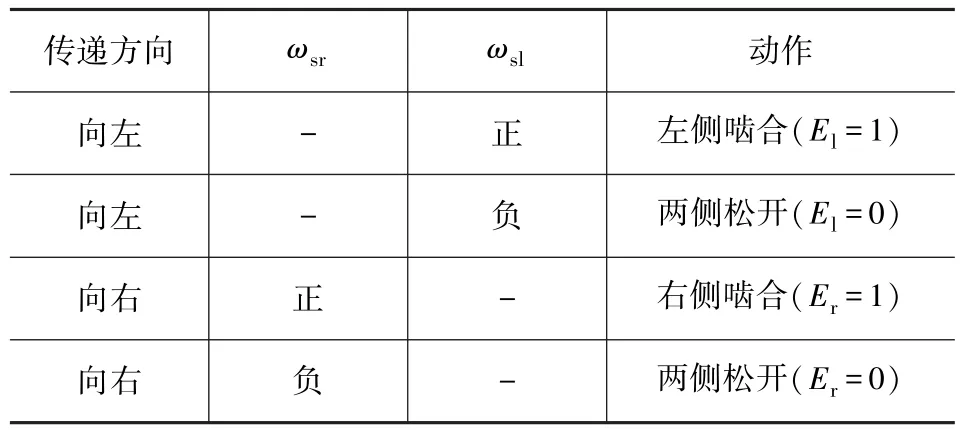
表1 主动差速器控制规则

其中，El和Er分别表示左、右两侧制动器的啮合状态，右侧驱动轴与两个制动器之间的速度差可表示为

式中:ωr为右侧驱动轴的转动速度；ωcl和ωcr分别为左侧和右侧制动器的转动速度。

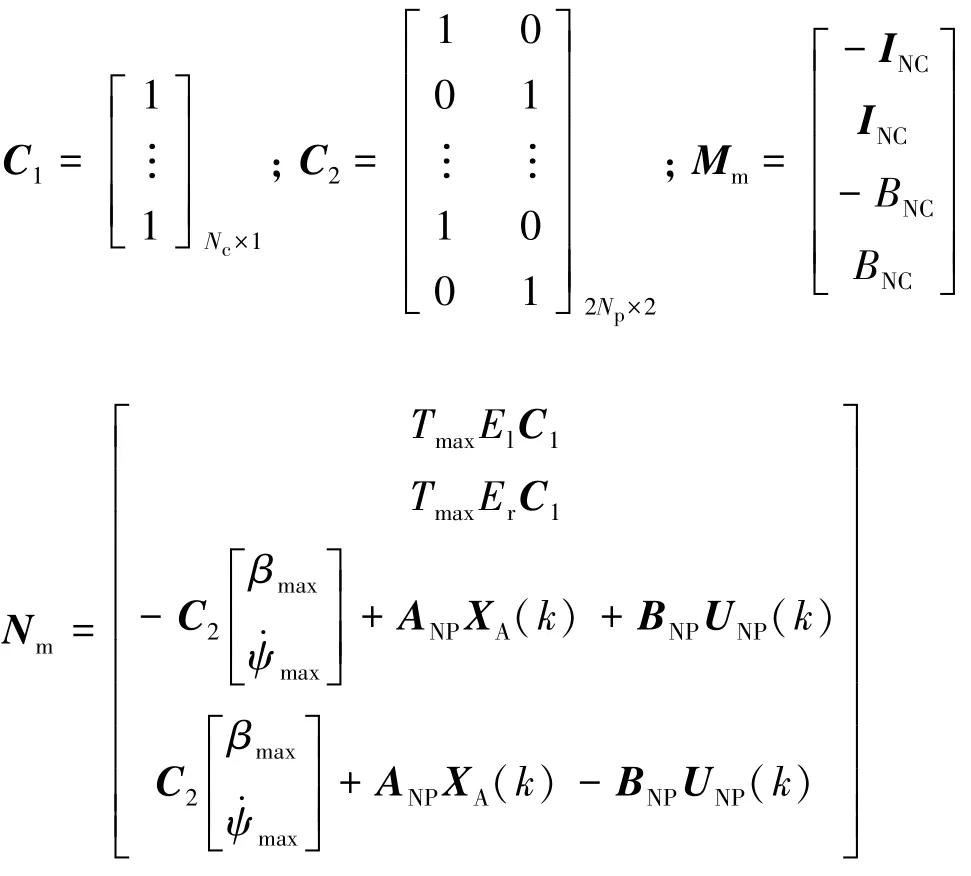
根据表1所示的主动差速器控制规则和控制力矩物理特性，可确定主动差速器控制力矩的Um(k)约束范围；根据式(16)、式(20)和式(21)，可确定车辆动力学预测模型的横摆角速度和车身侧偏角的约束范围。其不等式矩阵形式为

式中，Tmax为主动差速器左、右两侧制动盘的最大控制力矩极值。

其中:

2.3 模型预测控制求解

在模型预测控制问题的求解过程中，由于约束条件的存在，一般情况下难以直接得到式(17)的优化目标函数解析解，需要采用数值优化方法求解约束优化问题。由于目标函数是二次型的，动力学方程和时域约束条件是线性的，所以该约束优化问题可转化为标准的二次规划(quadratic programming，QP)问题描述。

将车辆动力学离散状态空间预测模型的输出变量(16)代入到模型预测控制的目标函数(27)中，并定义:

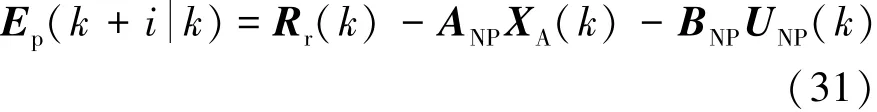
对目标函数进行整理，得

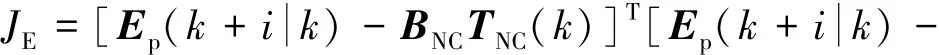
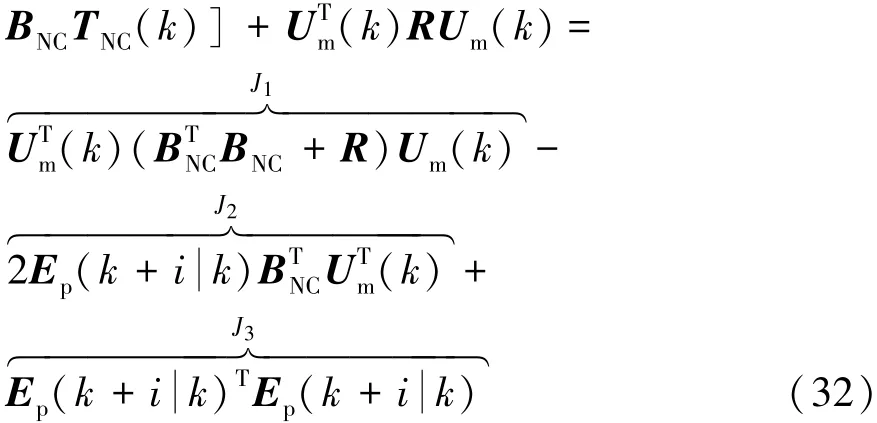
为获得二次规划问题的标准形式，设定二次规划问题中的相容Hessian矩阵为Em，且梯度向量的独立变量矩阵为Fm，分别表示为

由于式(32)中的常数项J3不影响主动差速器控制力矩序列Um的求解，因此，将以上两个变量矩阵代入到目标函数(32)中，并与约束条件不等式(30)进行整理和转换，得到如式(35)和式(36)所示的车辆操纵稳定性控制二次规划问题标准形式。利用内点法求解该带有线性约束的二次实函数，流程如图3所示(更加详细的求解过程请参考文献[14])。

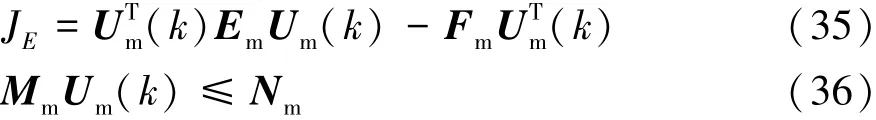
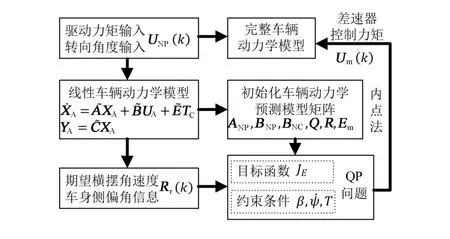
图3 约束模型预测问题的内点法求解

3 仿真结果分析

为验证模型预测算法在车辆操纵稳定性控制中的有效性，利用MATLAB/Carsim软件进行联合仿真分析。在转向盘角度正弦输入情况下，比较低附着系数路面上的模型预测控制车辆与无控制车辆之间的横摆角速度以及车身侧偏角参数变化，并分析主动差速器的工作过程及控制力矩变化。

本研究采用双轴线性车辆动力学模型用于模型预测控制系统设计，其主要参数如表2所示，而仿真模型则是装备了主动差速器的Carsim车辆动力学模型。

表2 车辆动力学预测模型参数

假设被控车辆以初始速度Vx＝20m/s在路面附着系数为0.5的湿滑沥青道路上行驶，对车辆施加如图4所示的正弦前轮转向角度，同时，为保证车辆的初始行驶速度及车辆模型的线性特性，主动差速器的输入转矩设定为86N·m，分别比较有主动差速器(图中AD曲线)和无主动差速器(图中OD曲线)工况下的控制力矩及车辆动力学响应特性，如图5～图7所示。

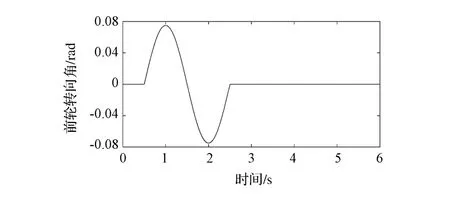
图4 车辆前轮转向角度

对于没有装备主动差速器的车辆而言，由于湿滑沥青路面的附着系数相对较低，当施加如图4所示的前轮转向角度时，车辆的前、后车轮侧偏角会快速增大，导致轮胎的非线性横向力很快达到其极限值(如图5所示)，难以为车辆转向提供所需的横摆力矩，其横摆角速度和车身侧偏角也会超过其极限值(如图6所示)。虽然经过3s之后车辆能够恢复稳定行驶状态，但在车辆的非稳态行驶过程中容易发生侧滑等问题，其安全性能难以得到保证。

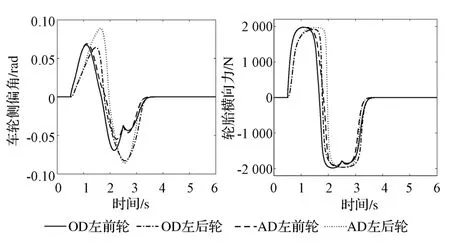
图5 前、后车轮侧偏角及横向轮胎力

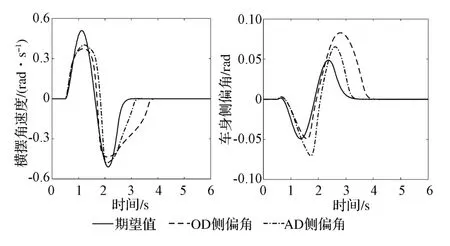
图6 车辆的横摆角速度及车身侧偏角

另外，从图7所示的车辆后轴驱动轮的滑移率及轮胎力变化情况可以看出，驱动轮在该工况下的最大滑移率为0.5%，远未达到10%的非稳态饱和值，其最大驱动力为594N，始终小于轮胎的最大纵向力1 565N(该值由轮胎力的非线性特性分析得到)。因此，可利用主动差速器对左、右两侧轮胎的驱动力矩进行主动分配，并通过差速驱动的方式产生补偿横摆力矩，进而提高车辆的操纵稳定性。

图7 后轴驱动轮滑移率及纵向力

而对于装备了主动差速器的车辆而言，当车辆的横摆角速度和车身侧偏角达到约束值时，文中设计的模型预测算法将会计算出期望的补偿横摆力矩，并根据主动差速器动力学特性，得到主动差速器左、右两侧制动器的控制力矩(如图8所示)，实现后轴上驱动力矩的横向转移和主动分配，进而使车辆的横摆角速度和车身侧偏角限定在最大极限值范围内，有效提高车辆的操纵稳定性。

图8 主动差速器控制力矩及后轴左右两侧驱动力矩

从仿真结果可以看出，利用车辆主动差速器产生补偿横摆力矩时，轮胎的最大纵向滑移率能够达到0.025，有效增大了轮胎纵向力的利用区域，同时保证了轮胎的纵向力始终处于线性范围内(滑移率小于0.1)。当车辆在湿滑沥青路上行驶时，虽然作用于主动差速器上的控制力矩会造成驱动力矩的部分损失，但车辆的行驶速度仅降低至19.34m/s，即仅降低3.3%(如图9所示)，表明主动差速器对车辆动力性的影响相对较小。

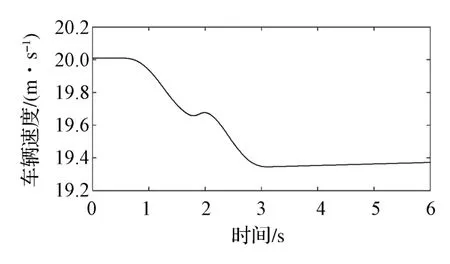
图9 被控车辆的行驶速度

4 结论

(1)提出的操纵稳定性模型预测算法基于线性车辆动力学模型进行状态预测，并对控制力矩、输出状态等多约束条件进行了分析，克服了单一线性预测模型匹配度差以及非线性预测模型计算量过大的问题。

(2)基于主动差速器的车辆操纵稳定性控制方法增大了驱动车轮在线性稳态区域内的纵向力利用范围，同时解决了传统差速制动稳定性控制造成的动力性能损失过大的问题。

(3)本研究仅对恒定速度的线性车辆动力学预测模型进行了研究，在进一步工作中，将充分考虑被控车辆的速度变化、轮胎力的非线性特性等影响因素，构建时变的模型预测控制系统并通过实车道路实验进一步验证其系统性能。

[1] ABE Masato.Vehicle handling dynamics:theory and application[M].Oxford:Butterworth-Heinemann，2015.

[2] HANCOCK M J， WILLIAMS R A， FINA E， et al.Yaw motion control via active differentials[J].Transactions of the Institute of Measurement and Control， 2007， 29(2):137-157.

[3] CANALE M，FAGIANO L.Comparing rear wheel steering and rear active differential approaches to vehicle yaw control[J].Vehicle System Dynamics， 2010， 48(5):529-546.

[4] HANCOCK M J， WILLIAMS R A， GORDON T J， et al.A comparison of braking and differential control of road vehicle yaw-sideslip dynamics[J].Proceedings of the Institution of Mechanical Engineers， Part D:Journal of Automobile Engineering， 2005， 219(3):309-327.

[5] 冀杰，李以农，陈翀.车辆主动差速器转矩横向传递及动力性能分析[J].机械科学与技术，2014，33(1):117-121.

[6] CANALE M，FAGIANOL，FERRARA A，et al.Vehicle yaw control via second-order sliding-mode technique[J].IEEE Transactions on Industrial Electronics， 2008， 55(11):3908-3916.

[7] DEL Re L， ALLGOWERll F， GLIELMO L， et al.Automotive model predictive control:models，methods and applications[M].London:Springer，2010.

[8] WONG A，KASINATHAN D，KHAJEPOUR A，et al.Integrated torque vectoring and power management framework for electric vehicles[J].Control Engineering Practice， 2016， 48:22-36.

[9] DE NOVELLISL，SORNIOTTIA，GRUBER P.Wheel torque distribution criteria for electric vehicles with torque-vectoring differentials[J].IEEE Transactions on Vehicular Technology， 2014， 63(4):1593-1602.

[10] SAWASE K，INOUNE K.Maximum acceptable differential speed ratio of lateral torque-vectoring differentials for vehicles[J].Proceedings of the Institution of Mechanical Engineers，Part D:Journal of Automobile Engineering， 2009， 223(8):967-978.

[11] 龚建伟，姜岩，徐威.无人驾驶车辆模型预测控制[M].北京:北京理工大学出版社，2014.

[12] WANG L P.Model predictive control system design and implementation using MATLAB[M].London:Springer，2009.

[13] RUBIN D，AROGETISA.Vehicle yaw stability control using active limited-slip differential via model predictive control methods[J].Vehicle System Dynamics， 2015， 53(9):1315-1330.

[14] ZHANG Y.Solving large-scale linear programs by interior-point methods under the Matlabenvironment[J].Optimization Methods and Software， 1998， 10(1):1-31.

[15] 冀杰.基于自动驾驶系统的车辆纵横向运动综合控制研究[D].重庆:重庆大学，2010.