辅助动力单元启动过程扭转振动的PID控制∗

钟必清，侯之超，刘瑞雪

前言

传动系统的扭转振动是影响混合动力汽车乘坐舒适性和安全性的一个重要因素。相对传统内燃机汽车，电机的引入使得混合动力系统的扭转振动特性发生改变，但也为振动的主动控制提供了新的途径[1]。

针对混合动力传动系统开展主动振动控制的公开文献，很大一部分是针对行星齿轮混合动力构型[2-4]。借助发动机与两个电机在转矩和转速之间存在的函数关系，可通过计算发动机曲轴转角以确定发动机转矩波动，再根据转矩波动量确定电机的输出转矩，从而控制发动机的转速波动[2]；或通过测取转速差等信息，利用PI控制[3]或滑模控制[4]确定电机补偿转矩来减小系统振动。

文献[5]中针对串联式混合动力挖掘机的轴系扭振问题，以液压泵负载变化为干扰量，采用模糊PID控制来减小轴系振动。

针对含ISG或BSG的混联式混合动力系统，文献[6]中设计了一种协调控制策略，通过提取运行过程中系统的振动相位和幅值，对电机施加反相转矩实现对系统振动的主动控制。其中快速、准确地提取系统的振动信息是关键。文献[7]中对比研究了传统内燃机与混合动力系统，在换挡过程采用PID算法分别控制发动机和电机的输出转矩，显示电机的快速响应能大幅度地减小换挡过程的振动。文献[8]中对混合动力系统进行台架试验，分析基于转速误差、预测转矩前馈和设定转矩前馈等3种主动控制的效果。文献[9]中基于部件特性建立动力系统的预测模型，通过对电机转矩的控制来保证动力输出和车速的平稳。文献[10]中设想改变ISG电机极对数和气隙结构，使电机随转速变化产生周期性电磁转矩脉动，以抵消发动机的波动。如何可靠地产生同频等幅的反相转矩脉冲是个难点。

上述围绕动力传动系统扭振控制的研究，通常不考察控制过程中系统启动时间和能量消耗的变化，也未见文献探讨控制电机转矩响应速度对控制效果的影响。

为此，本文中以某混联式客车混合动力系统为对象，研究启动过程中辅助动力单元(auxiliary power unit，APU)的扭转振动及其主动控制。该APU由发动机、ISG电机和中间的扭转减振器组成。综合考虑系统振动水平、启动时间和能量消耗3项性能要求，依据敏感系数法确定各目标权重以将控制问题转换为单目标优化。进而设计PID控制策略进行主动扭振控制。最后结合算例探讨控制参数、ISG电机响应速度等系统参数对控制效果的影响。

1 系统模型与参数标定

图1示出一种同轴混联动力传动系统辅助动力单元，它包括发动机、扭转减振器和ISG电机。图中，Tisg和Tice分别为ISG和发动机的转矩，后者包括气体力矩Tice_gas、往复惯性力矩Tice_iner和摩擦力矩Tice_fric。本节中推导该系统的动力学方程，并引入PID控制而建立其状态方程，进而阐述了初始状态与系统参数的标定方法。

1.1 系统动力学模型

应用牛顿第二定律，可得到系统的扭振力学方程:

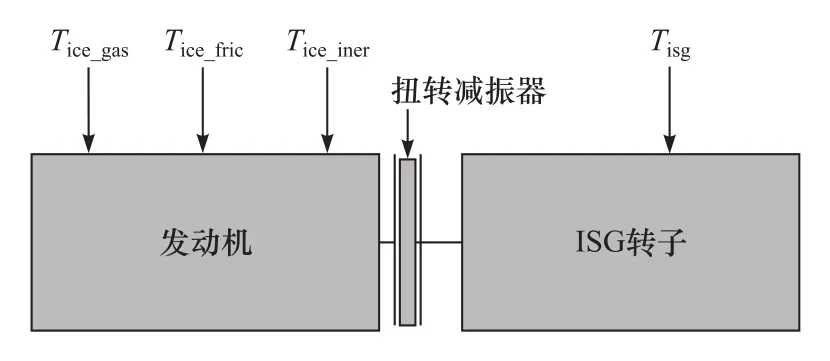
图1 发动机-ISG系统结构与受力示意图

式中:φ1和φ2分别为发动机和ISG电机的转角；k1(φ1，φ2)为扭转减振器的刚度，是扭转角 φ1和 φ2的分段线性函数；c为扭转减振器的阻尼；I1和I2分别为发动机和ISG电机的转动惯量。

为便于设计并实施主动振动控制，对发动机各力矩分别进行简化[11]。其中，Tice_fric采用稳态模型，另外两个力矩分量则分别简化为

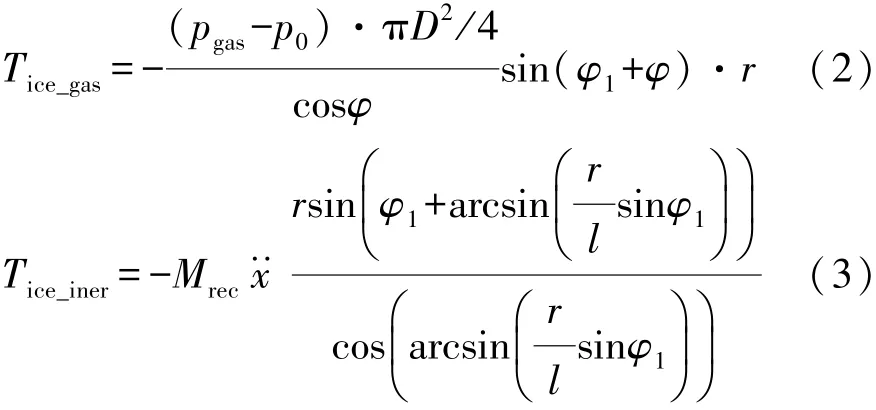
式中:D为活塞直径；p0为标准大气压；φ为连杆摆角；φ1为曲柄转角；r为曲轴回转半径；l为连杆长度；x··为活塞位置的二阶导数；Mrec为等效活塞质量。

1.2 状态方程

引入控制变量 u，并将式(1)转化为状态方程[11]:

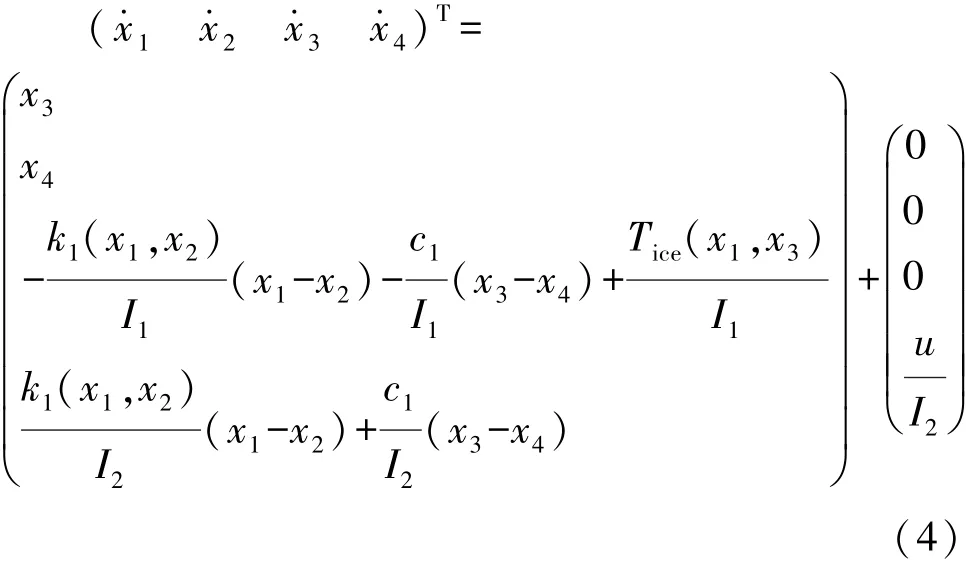
选取发动机与电机转速差作为误差项，采用PID控制，控制变量u依据下式确定:

式中:T0为ISG电机的前馈转矩；P，I和D分别为比例参数、积分参数和微分参数。针对具体的电机转矩响应时间，依据经验分别选取多组PID控制参数进行仿真计算，并以综合性能指标最小的那组作为该电机转矩响应速度对应的最佳控制参数。

基于上述推导与简化，动力学与控制建模结构示意图如图2。通过曲轴实时转角、转速信号配合系统参数可计算出发动机激振力矩；引入发动机与ISG电机转速差作为PID控制的误差项，ISG电机实时转矩由目标前馈转矩T0和PID主动控制转矩合成。

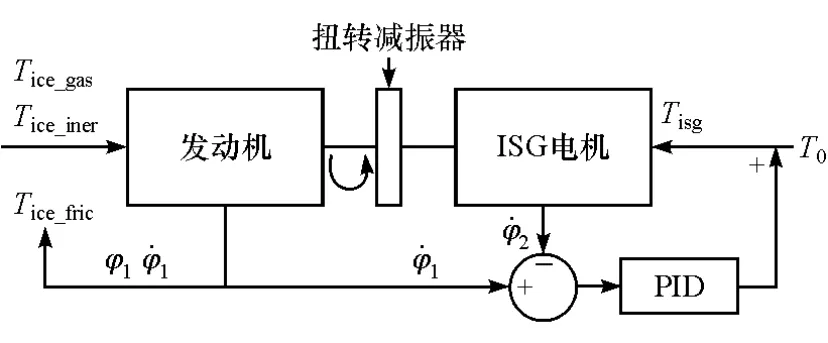
图2 系统动力学与控制结构示意图

1.3 系统初始状态与参数标定

鉴于每次启动前系统的实际状态并不相同，而发动机力矩表达式是基于简化理论得到，为得到较高的仿真精度，结合GT-Power仿真和台架试验对模型初始状态和系统参数进行识别与修正。

识别与修正思路简述如下:在台架试验中通过CAN总线及数采设备直接采集ISG实时转矩等信号，经过处理，得到发动机、ISG电机的实时转速和转角，然后计算扭转减振器的实时转矩。对比试验与仿真得到的转矩和转速等动态响应，对各参数进行识别或修正。这样处理的参数主要有发动机曲轴初始转角φ1、ISG电机转矩响应时间常数τisg、往复气体力修正系数Z、减振器阻尼系数c和发动机系统静摩擦力矩Tice_fric。

2 性能评价与权重计算

为综合考虑汽车的动力性、舒适性和经济性，可用于评价主动控制性能的指标主要有3个，即启动时间t、振动大小V与启动过程中的能量消耗W。作为初步尝试，将3个目标转化成单目标评价函数

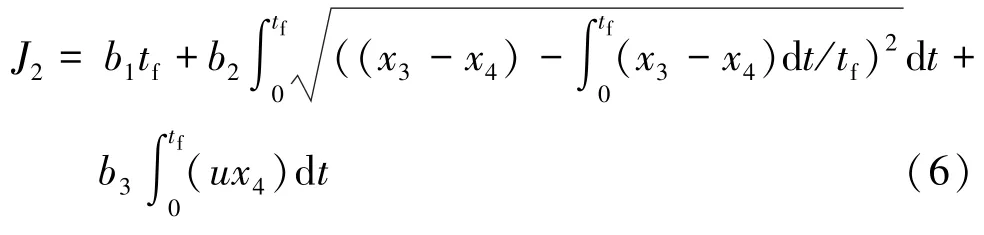
式中:bi(i＝1，2，3)为各权重系数；tf为电机拖动发动机到怠速控制时所需时间；u为ISG电机实时输出转矩。综合性能指标J2越小表明控制效果越好，理想状况是启动时间短、振动小且耗能少。

通过敏感度分析确定式(6)中的各权重系数。考虑ISG电机的极限转矩与最小启动转矩，以不同恒转矩启动系统，考察系统各指标变化，然后进行敏感度分析和归一化处理。

假设ISG电机以i个恒转矩分别启动，依据仿真结果统计得到启动时间、振动大小和能量消耗指标ti，Vi和Wi的具体数值。选择某一组指标作为基准，设为t0，V0和W0，并计算各组相对基准变化的比例:

其中:Psum＝∑Pti+∑PVi+∑PWi

取历次运行中3项指标各自最大值，结合式(8)所示无量纲参数得到各权重系数:

3 算例

3.1 系统参数

对于某混合动力系统APU，其发动机和ISG电机的转动惯量分别为1.52和2.14kg·m2，ISG电机的极限转矩为±600N·m，减振器刚度曲线如图3所示。

经过台架试验标定的系统初始参数如表1所示。应用表中参数，ISG电机以300N·m的恒定转矩起动发动机时的仿真与试验结果对比见图4和图5。

图3 减振器刚度曲线

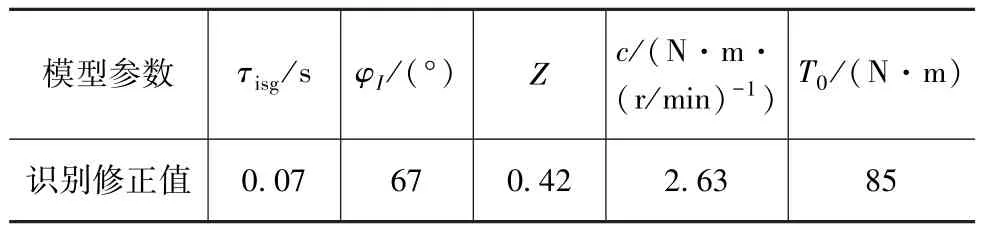
表1 模型参数识别与修正值

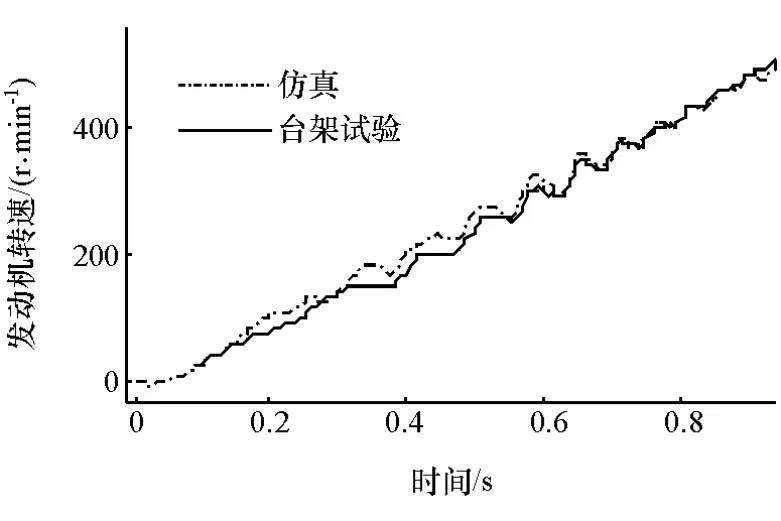
图4 发动机转速对比

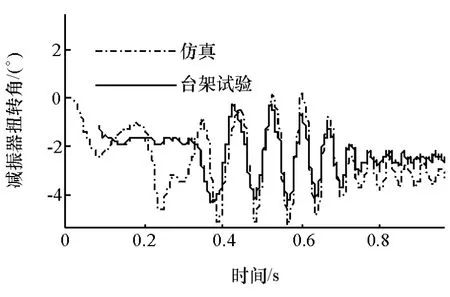
图5 减振器扭转角对比

由图4和图5可见，在发动机起动过程中，应用标定参数计算得到的转速波动、减振器扭转角与台架试验结果吻合良好，说明所建立的模型及识别得到的参数可用于表征所研究APU系统的运行状态。

基于敏感性分析确定的控制性能评价函数权重系数为:b1＝0.426(s-1)；b2＝0.319(s/rad)；b3＝1.13×10-5(kJ-1)。

3.2 振动控制效果分析

为全面分析振动控制效果，首先分忽略或考虑电机的转矩响应时间两种情况，通过仿真计算考察执行器性能对主动控制效果的影响；然后选定电机的转矩响应时间，讨论各控制参数与控制效果之间的关系。

有递减规律的三种情况：一是区块产量有明显规律，直接拟合递减率；二是区块产量没有明显递减规律，但平均单井产量有明显递减规律的取平均单井产量递减率；三是与开发历史背景及开发方式结合，分阶段、分构成、分开发方式拟合递减规律。

3.2.1 基于理想电机的控制

假设理想电机的转矩响应时间常数为0，据此进行PID振动控制。实施主动振动控制前后，系统响应和性能如图6～图10和表2所示。

图7 控制前后发动机转速

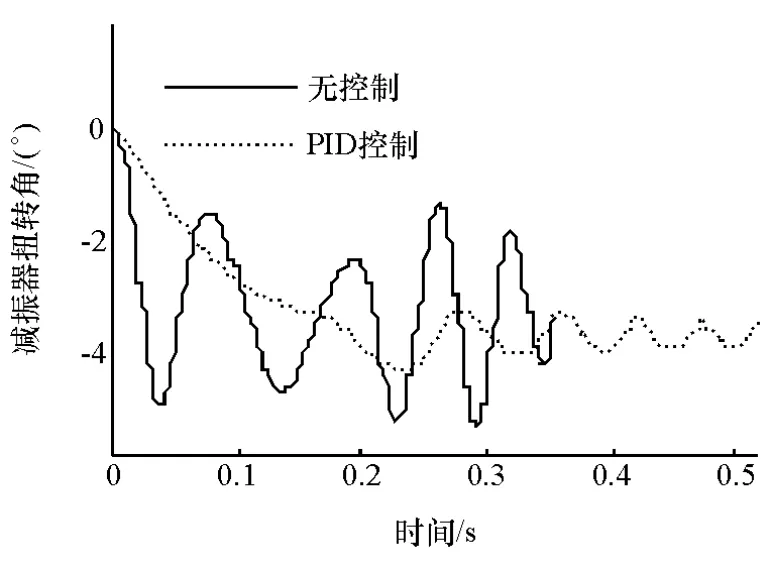
图8 控制前后减振器扭转角

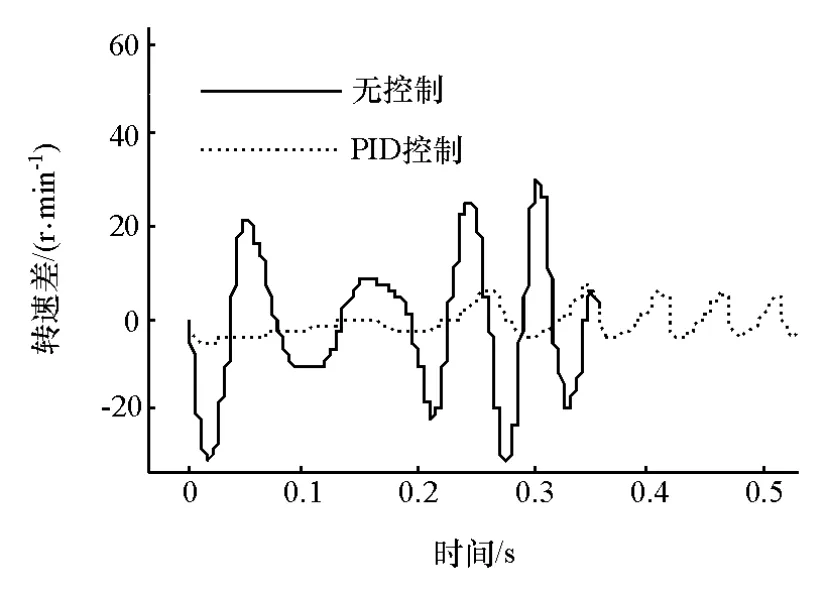
图9 控制前后发动机-ISG电机转速差

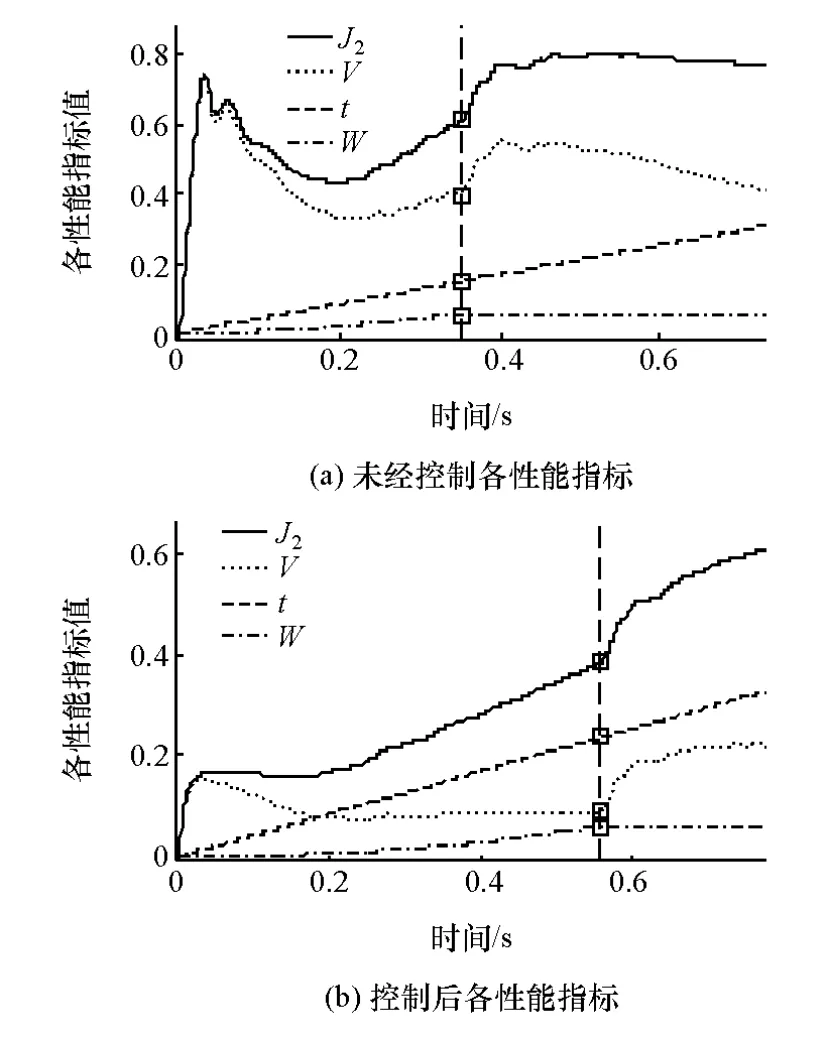
图10 控制前后各性能指标时程曲线

表2 主动控制前后性能对比

图6显示了因实施主动控制，电机输出转矩在系统启动过程中的变化历程。刚启动时，电机与发动机转速差较大，为避免引起破坏，电机输出转矩降低；随着发动机转速的升高，电机输出转矩又增大以降低启动时间。之后因发动机气体力的周期性波动，ISG电机输出转矩也作周期性调整以稳定电机与发动机的转速差。从图7可见，应用PID控制后，发动机转速上升较慢且周期性波动幅值减小，系统启动时间延长。

图8显示，进行振动控制前后，系统启动过程中减振器扭转角的幅值由反向的4.3°降低为3.8°，变化不大；但扭转角波动的幅值却从3°降低到1°以下，平稳渡过400r/min的共振区。图9则显示应用PID控制后，发动机与ISG电机的转速差显著减少，其变化趋势与减振器扭转角基本一致。

图10为控制前后各性能时程曲线对比，其中时间项曲线基本一致；方框标识是发动机转速到达500r/min而ISG电机停止输出转矩的时间点。由图可见:综合性能曲线整体变化较为复杂，其波动主要由振动项引起；时间项呈线性上升；能量项整体占比较小，随时间近似线性增加。结合图9可知:刚启动时，如无控制，转速差快速增加而引起振动项急剧上升，随后因气体力矩的周期性变化而发生周期性波动；实施控制后，转速差幅值大幅降低，振动项几乎呈水平状态通过共振区。

3.2.2 电机转矩响应时间影响分析

对于内置式永磁同步电机，其最短转矩响应时间可达到15ms[12]。参照该值，为ISG电机设定不同的转矩响应时间常数，分别求得PID控制的最佳控制参数和性能评价值，见表3，其中J02与J12是控制前后系统的综合性能指标。

表3 电机转矩响应时间与PID参数及控制性能

基于表3所示电机转矩响应速度与PID控制参数实现振动控制，3个分项性能随电机转矩响应时间常数τisg的变化如图11～图13所示。

从表3中可以看出，随着电机转矩响应时间的延长，控制效果逐渐变差。当响应时间为0.05s时，控制前后综合性能指标都为0.51，由图12可知，此时系统平均转速差由控制前的9.2减小到7.6r/min，减振效果已不明显。因此，有效的PID主动控制要求ISG电机的转矩响应足够快；电机转矩响应速度越快，减振效果越明显。

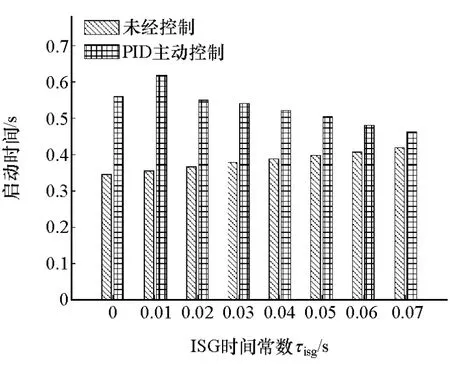
图11 启动时间

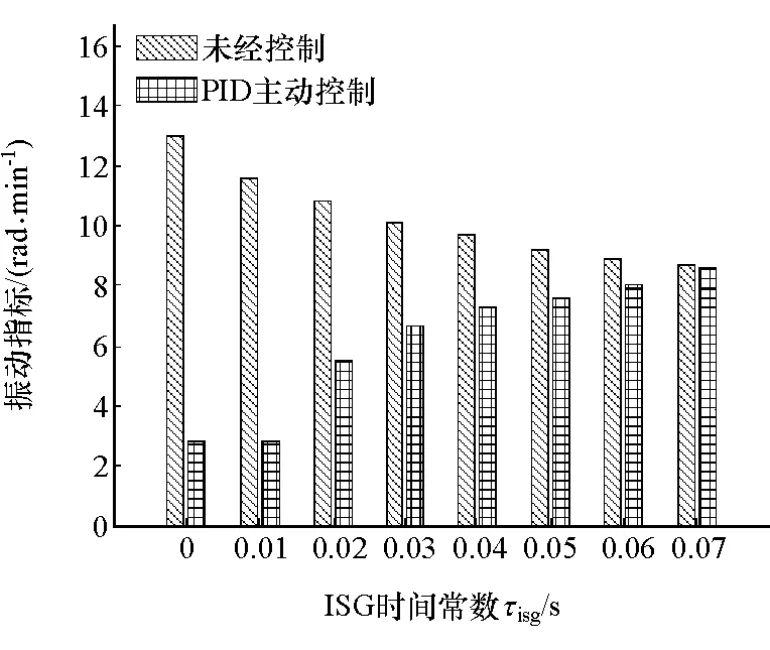
图12 振动指标

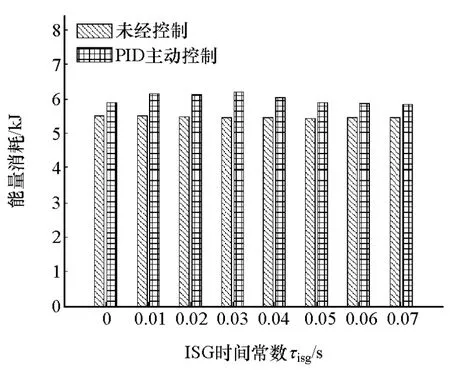
图13 能量消耗

图11 显示实施主动控制后，对于转矩响应越快的电机，为达到好的减振效果，APU系统启动时间延长越多。图13表明:施加主动控制后，系统能量消耗均有少量的增加；该增加量随电机转矩响应速度的变化趋势比较复杂，但是变化幅度差别很小。

3.2.3 控制参数影响分析

下面分别研究P，I和D 3个控制参数对主动控制效果的影响。仿真结果显示:对应不同的电机转矩响应时间，控制参数对控制效果的影响规律差别不大。基于性能需要通过尝试确定P，I和D的上限。下面仅给出电机转矩响应时间为0.02s，控制参数在上限范围内的部分结果，如图14～图16所示。其中，方框标识是发动机转速到达500r/min而ISG电机停止输出转矩的时间点，图16是图15中矩形框局部放大图。

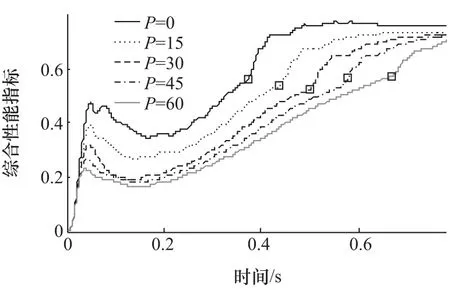
图14 比例参数P与性能指标J2(I，D＝0)

从图14可以发现，比例控制参数P对综合性能指标J2的影响较大，并存在一个最优值。图15是P＝0而I，D等间隔取值时综合性能指标的时程曲线。可以发现:随微分参数D从零增大，启动时间逐渐延长，PID控制在启动结束时刻综合效果先变好再变差。图16所示为局部曲线显示:I参数在[0，30]区间取值时PID主动控制效果几乎没有差别；而当I取45，发动机起动结束时系统性能变差。

结合3张图可知:P参数在3个控制参数中起主导作用，其值的大小决定了转速差波动的消减幅度；I参数能消除系统稳态误差，但会延长系统响应时间；D参数能捕捉到转速差变化趋势，提前改变电机输出转矩，从而改善启动过程的动态性能。

以上结果充分说明，正是利用了电机转矩快速响应的能力，才能改善APU系统启动过程扭转振动和综合性能。

4 结论

针对一种辅助动力单元，本文中推导了系统的非线性扭振方程，建立了具有PID控制的状态方程，在AMESim中建立了具有PID控制的系统扭转振动的仿真模型，并应用台架试验对系统参数进行了标定。在此基础上，综合考虑启动速度、振动控制与能量消耗等需要构建了单目标性能评价函数，基于敏感度分析确定了各加权系数。最后针对ISG电机不同的转矩响应速度，基于性能最优确定了相应的最佳控制参数，实现对APU系统启动过程中扭转振动的PID控制。算例结果得到如下结论。

(1)不考虑ISG电机的转矩响应引起的滞后，PID控制能有效降低APU系统在启动过程中的扭转振动，而不会明显增加系统能耗与启动时间。

(2)对于实际ISG电机，只有当其转矩响应足够快时PID控制才能使APU系统在启动过程中具有较好的综合性能。控制参数P对控制效果具有显著的影响，参数D能稍微改善综合性能，参数I影响不明显。

[1] 闫明刚，张勇，侯之超，等.混合动力客车传动系扭振响应及其影响因素分析[J].工程力学，2014，31(S1):223-227.

[2] ITO Y，TOMURA S，SASAKI S.Development of vibration reduction motor control for hybrid vehicles[C].The 33rd Annual Conference of the IEEE Industrial Electronics Society， Taipei:IEEE，2007:516-521.

[3] SYED F U，KUANG M L，HAO Y.Active damping wheel-torque control system to reduce driveline oscillations in a power-split hybrid electric vehicle[J].IEEE Transactions on Vehicular Technology，2009，58(9):4769-4785.

[4] KOU Y S，WESLATIF.Development of a hybrid powertrain active damping control system via sliding mode control scheme[C].SAE Paper 2013-01-0486.

[5] 张贝贝，刘少军，胡琼.混合动力挖掘机轴系扭振的主动控制仿真[J].噪声与振动控制，2016，36(4):97-102.

[6] KIM Y S，PARK J，PARK T W，et al.Anti-jerk controller design with a cooperative control strategy in hybrid electric vehicle[C].Conference on Power Electronics， Jeju:IEEE，2011:1964-1968.

[7] WALKER PD，ZHANGN.Active damping of transient vibration in dual clutch transmission equipped powertrains:a comparison of conventional and hybrid electric vehicles[J].Mechanism and Machine Theory，2014.77:p.1-12.

[8] MORANDIN M， BOLOGNANI S， FAGGION A.Active torque damping for an ICE-based domestic CHP system with an SPM machine drive[J].IEEE Transactions on Industry Applications，2015，51(4):3137-3146.

[9] VADAMALU RS，BEIDL C.MPC for active torsional vibration reduction of hybrid electric powertrains[J].IFAC-Papers On Line，2016，49(11):756-761.

[10] ZHANG J， HUY， YANG F， et al.Simulations on special structure ISG motor used for hybrid electrical vehicles aimed at active damping[C].SAE Paper 2017-01-1123.

[11] 闫明刚.混合动力客车传动系统扭振分析及控制[D].北京:清华大学，2015.

[12] 黄文卿.混合动力车用永磁同步电机控制参数估计与控制策略研究[D].北京:北京理工大学，2014.